基于MCS和AlexNet的水潤滑推力軸承故障檢測*

柯 喆,關博凱,王子豪,朱慶龍,鮑曉華

(1.合肥工業大學 電氣與自動化工程學院，安徽 合肥 230009；2.合肥恒大江海泵業有限公司，安徽 合肥 231131)

0 引 言

大型潛水電機常作為搶險救災排水設備廣泛應用于地底礦山抽水、洪水搶險及城市污水系統堵塞等場景[1]。大型潛水電機工作環境惡劣，且常因過載、氣泡及熱脹冷縮等原因，導致軸承磨損。因此，異物容易進入軸承中，特別是立式潛水電機中的水潤滑推力軸承，異物劃損軸承盤表面使應力發生改變會使水潤滑推力軸承迅速進入故障狀態導致轉矩不平穩、噪聲大，嚴重時甚至導致定子繞組燒毀[2]，嚴重影響了搶險救災效率及民眾生命安全。目前，軸承故障診斷領域多采用振動信號對故障信號進行分析，具體的方法是在水泵機體不同位置安裝加速度傳感器，通過對采集的振動信號進行分析，這種方法具有理論和實踐基礎，無論是傳統的小波分析、包絡譜分析和經驗分解等傳統信號分析處理的方法或者是新興的機器學習等提取信號特征值進行判斷的方法[3-5]，常能較為容易地尋找到故障信號并進行診斷。然而分析振動信號所需的加速度傳感器及配套系統常常較為昂貴，考慮到潛水電機常在深水區域工作，拆裝加速度傳感器成本巨大，且水阻尼會產生大量噪聲淹沒故障信號，業界急需一種便捷且行之有效的方法對軸承故障進行診斷。

在機械結構的視角中，軸承故障會導致原本與電機定子同心旋轉的轉子在軸承滾珠經過故障點時發生偏移。從電磁的視角來看，這種轉子物理上的偏移會導致氣隙分布不均勻從而引起電機的電流變化。因此,使用電機電流信號(MCS)對故障進行檢測具有堅實的理論基礎。在文獻[6]中，提出了使用MCS對電機狀態進行分析的方法，同時提出了不同軸承在不同損壞情況下的故障頻率計算公式。然而在實際應用中，故障信號與基頻信號間存在低信噪比的特征，且軸承故障所引起的沖擊性信號常被主波諧波、開槽諧波、飽和諧波以及環境噪聲等掩蓋，導致傳統的分析方法難以鎖定頻域中的故障頻率。隨著計算機硬件的發展及機器學習、深度學習等算法模型的更新迭代，提取信號特征參數訓練預測模型實現對健康信號和故障信號分類的方法被大量提出[7-9]。然而此類方法還是基于振動信號進行故障診斷，且研究對象均不是潛水電機故障。

目前，對潛水電機進行系統化的狀態檢測報道較少，因此潛水電機的故障信號，特別是采用了水潤滑推力軸承的立式潛水電機電流故障信號獲取較為困難。本文通過分析水潤滑推力軸承的故障機理提出了一種能有效仿真該軸承故障的數字模型并得到不同工作狀態下電機的健康和故障電流信號[10]，并分別在健康電流信號和故障電流信號中加入隨機正態分布信號模擬環境噪聲。經過時移的方法消除基波及其三倍數次諧波分量加大信噪比，突出噪聲信號。隨后通過一系列預處理方式將電流信號轉化為二維的圖片，并經過AlexNet模型的訓練最終得到分類模型。最后，通過測試集進行驗證，準確率符合預期。

1 推力軸承故障電流分析

實際故障推力軸承如圖1所示，當異物進入軸承內部時，將破壞推力瓦體表面并產生劃痕，造成持續但輕微的轉矩波動；當異物經過溝槽時，由于運動幅度較大，將會產生較為明顯的沖擊性轉矩波動。兩種轉矩波動將改變氣隙磁密的分布，并最終產生相應性質的電流擾動。

圖1 故障推力軸承

1.1 水潤滑推力軸承單點故障模型

本文基于文獻[10]中的單點軸承故障模型提出了一種推力軸承單點故障的數字模型，此處的單點故障與常規的滾珠軸承定義的單點故障略有不同，常規滾珠軸承單點故障指軸承內圈道、外圈道或滾珠上任意一處損壞，而推力軸承單點故障指進入異物隨盤體旋轉而旋轉。此模型使用固體導磁材料代替氣隙中的空氣，用改變磁導率的方法將故障擾動引起的氣隙長度不均勻的物理特性轉化為了可以在仿真軟件中實現的電磁特性。氣隙磁動勢的方程為

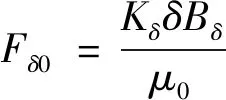
(1)

式中:Fδ0為氣隙磁動勢；Kδ為開槽系數；δ為氣隙長度；Bδ為最大氣隙磁密；μ0為真空磁導率。

由式(1)可得，當模型其他參數不發生改變時，氣隙長度與磁導率成正比。

本文中采用的仿真模型參數如表1所示。

表1 模型基本參數

仿真模型如圖2所示，圖2(a)為模型簡圖，其中氣隙磁密部分被分為了若干個區域，深色區域代表了溝槽部分，淺色區域代表推力瓦部分。使用固體磁導可變的導磁材料對這些區域進行填充，本文簡化了仿真模型，設定在一個旋轉周期內的任一時刻，只有沿軸中線的對應2個區域的磁導率發生改變，其余區域的相對磁導率均為1。值得注意的是，圖2(b)所示的用于有限元分析的仿真模型中的轉子和導磁材料間填充了一層極其稀薄的空氣，這層空氣的作用是避免固體導磁材料和轉子部分的摩擦。

圖2 模型解析圖與仿真圖

1.2 電流信號構建及降噪

實際采集的故障電流信號主要包含基波及其三倍數諧波，類正態分布的環境噪聲和軸承故障信號三個分量[11]。在此，需要先定義信號的概念，本文中“信號”指與軸承故障相關的信號，即軸承故障信號；“噪聲”指除故障信號外其余的所有信號分量，例如基波分量。因此，信噪比的方程為

(2)

式中:r為信噪比；Sf為與故障有關的信號；Ss為與故障無關的信號。

通常，軸承故障信號視為周期沖擊信號，滾珠軸承的信號頻率根據軸承尺寸、滾珠數目、偏斜角度等參數有相應計算公式[6]。然而關于止推軸承的故障頻率計算式研究仍有不足，本文通過深度學習的方式研究信號在時域上的表現，并不需要相應的故障頻率計算公式，但要盡可能地提升信噪比，而時移是一種較好的增強信噪比的方式。

將軸承故障視為沖擊性負載，則負載轉矩可視為

TL(t)=TL0+N(t)+TB(t)=

(3)

式中：TL0為低頻負載；N(t)為呈高斯分布背景噪聲分量；TB為幅值為A的沖擊故障負載；fc為故障頻率。

將沖擊故障負載展開為傅里葉級數：

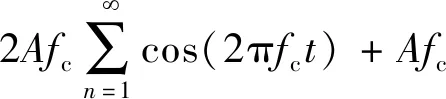
(4)

考慮到式(4)、式(3)可寫為

(5)

式中：ωc為故障角速度；Tmb為故障引起的轉矩脈動常量。

文獻[6]中提出了轉矩脈動和電流調制信號之間的系數是一個阻尼系數，因此故障電流信號可以表示為

(6)

式中：iH(t)為健康狀態的電流信號；βn為阻尼系數，隨n的增加而衰減；ωs為供電角速度。

式(6)可進一步改寫為

iF(t)=Imcos(ωst)+

(7)

時移可以大幅度削減主波，其原理圖如圖3所示，噪聲中最大的成分是基波及其諧波，通過將采集信號在時域上延時半個周期，從而使近似正弦信號的部分大量抵消，可以在保留信號特征的同時大量降低噪聲分量。

圖3 時移原理圖

在應用時移的方法后，混合時移信號可以表示為

(8)

式中：imixed為混合后的時移信號；ires為殘余信號；fs為供電頻率。

在時移后，理論上電流的主波被抵消，而故障信號由于與主波信號不同頻率，故未抵消。

如圖4所示，圖4(a)中的信號為加入隨機正態分布噪聲后的原始故障電流信號及其頻譜，此處添加的背景噪聲既模擬了真實環境下的背景，又能避免后續訓練的模型過擬合，加強了模型整體的魯棒性；圖4(b)中的信號為時移后的信號及其頻譜，可以明顯地看見時移大大降低噪聲分量，提高了信噪比。

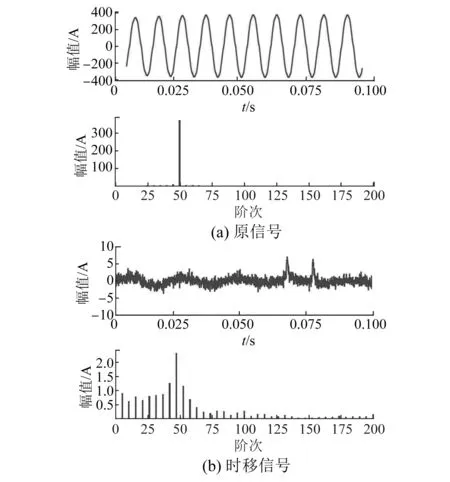
圖4 原信號與時移信號時頻對比

2 信號1D-2D預處理

目前，較為出色的深度學習模型往往被應用于計算機視覺領域，即為圖像分類、分割和目標識別所設計。模型的輸入有統一標準，均為3通道，尺寸為224×224的RGB圖片，針對灰度圖進行分析時，標準為1通道，尺寸不變。因此，本文對仿真所得的電流信號進行預處理，通過采樣窗口對原信號分段，并對每段子信號進行重構，使一維的電流信號轉化為二維灰度圖像，以便導入模型中進行分析。

本文中電流信號的采樣頻率為20 kHz,采樣時間為8 s，潛水電機轉速為1 465 r/min，設定每轉的時間間隔0.02 s為一個故障周期，可得每個故障周期包含了400個采樣點，因為采樣窗口大小需為n×n，以便隨后重構，所以采用的采樣窗口取4個故障周期，即1 600個采樣點大小。

現將一個子信號按時間序列構成的矩陣表示如下：

(9)

將此序列按升序重構為方陣：

(10)

實際與仿真所采集的電流信號可近似視為離散的正弦波形，即采樣點的幅值介于區間[-Imax,Imax]。灰度圖亮度為介于[0,255]的像素點，若將每個采樣點視為灰度圖的一個像素，則需要將電流幅值轉化為亮度幅值。考慮到神經網絡均是基于梯度下降的方法優化代價函數，為使代價函數的梯度足夠大且具有足夠的預測性，本文采用了Sigmoid函數將電流幅值映射為亮度值，其函數表達式為

(11)

歸一化處理后，與電流幅值相比，其各亮度值之間存在更大的梯度。

將子信號方陣轉化為尺寸為n×n的灰度并重構尺寸為224×224，方便后續神經網絡處理，如圖5所示，其中故障部分為明顯的水平白色橫條，對應了故障信號所在的波峰位置。

圖5 原信號與時移信號三維可視化圖片對比

3 基于AlexNet的推力軸承故障診斷方法

通常來講，數據集的大小和維度決定了學者選擇神經網絡模型的傾向，使用同樣的訓練集，較深的神經網絡往往可以實現更高的準確率。然而訓練較深的神經網絡耗時也更多，考慮到軸承故障診斷的實時性，本文基于AlexNet卷積神經網絡(CNN)模型提出了一種通過MCS診斷推力軸承故障的方法[12]。

3.1 AlexNet模型

AlexNet作為一種經典的CNN，與CNN網絡因采用了ReLu不飽和激活函數和Dropout正則化策略相比，顯著降低了模型的過擬合的同時加快了訓練速度[12]。原AlexNet模型受限于當時硬件條件采用了雙圖形處理器(GPU)并行訓練的方式，因此存在2個完全相同的神經網絡結構，本文采用單個網絡結構對故障信號進行分析。如圖6所示，輸入為1×224×224的灰度圖像，經過多個卷積核的處理后展平進入線性連接層最終得到n個代表歸屬各類概率的輸出。

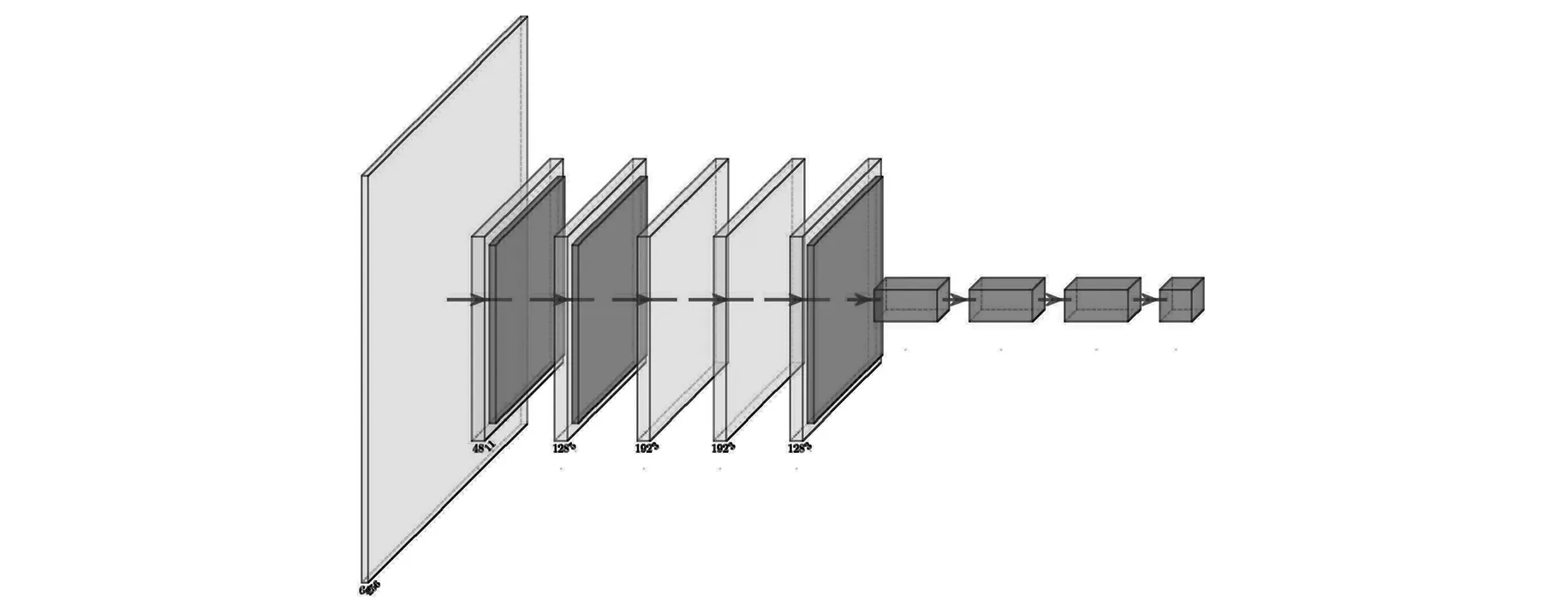
圖6 AlexNet網絡結構

各卷積層、池化層、連接層的參數如表2所示。

表2 AlexNet結構

3.2 診斷試驗過程

試驗流程如圖7所示，具體步驟如下：

(1) 輸入信號并加入正態分布的背景噪聲。此處的正態分布函數由基于Python平臺的標準正態分布函數生成，幅值參數設置為0.3。

(2) 時移。

(3) 將信號按照設計大小的窗口分段取樣，窗口大小為1 600個采樣點，即為0.08 s，隨后將采樣窗口得到的信號重構為方陣。

(4) 使用Sigmoid函數處理方陣。

(5) 將方陣轉化為灰度圖。

(6) 分割數據集為訓練集和測試集，其中80%被劃分為訓練集，20%被劃分入測試集，輸入到AlexNet網絡中開始訓練。

(7) 反復訓練后輸出預測模型。

圖7 診斷流程圖

3.3 試驗結果及分析

本次試驗生成了8 000個樣本，其中80%用于訓練集訓練，20%作為測試集。訓練輪數為40輪，每輪訓練2 000次，每一輪輸出一個預測模型，并用測試集進行檢測，輸出整體損失和模型準確率。訓練完成后保留準確率最高的模型，試驗結果如圖8所示，其中再訓練輪數為28次時，模型達到最大準確率99.87%。在30輪后，模型準確率基本穩定。

圖8 試驗結果

4 結 語

本文基于水潤滑推力軸承實際故障機理，提出了一種可用于有限元仿真的故障推力軸承數學模型。在仿真得到的故障電流信號中加入隨機正態分布的背景噪聲信號模擬實際故障信號。針對故障信號混淆在基波及其諧波分量中難以觀察的問題，應用了時移的處理方法，將信號延遲半個周期后與原信號相加從而使基波及其諧波分量大大減少，增強了信噪比。隨后，為實現智能識別的目的，將一維的電流信號通過一系列預處理轉化為深度學習可以訓練的二維灰度圖，通過較淺的AlexNet模型對健康信號和故障信號進行訓練得到預測模型，結果表明，所得的預測模型準確率為99.87%，較好地實現了預期目標，為基于電流信號的水潤滑推力軸承單點故障檢測提供了新的思路。