機械臂伺服傳動系統機電耦合建模及矢量控制分析

汪濤，陶小培

漯河職業技術學院，河南 漯河 462000

0 引言

本次研究立足于Park與Clark變換，運用MATLAB軟件構建串聯型機械臂系統機電耦合模型，利用SVPWM技術構建伺服控制系統，通過對電機進行耦合控制，確保電機磁矩與電流轉矩相互獨立運行，實現伺服傳統系統解耦。

1 永磁同步電機介紹

常見的串聯型機械臂內部均安裝有永磁同步電機，此類電機是在三相同步電機的基礎上發展而來，其最大的優勢在于利用永磁體代替電勵磁系統，有效解決了勵磁線圈、電刷對于電機運行造成的干擾。電機啟動之后，三相電流進入定子繞組，定子繞組通電之后會在其內部形成旋轉磁場，旋轉磁場作用于電機內部的轉子，使轉子開始運動，待轉子的轉速與旋轉磁場的磁極轉速保持一致時，永磁電機進入正常工作狀態[1]。

根據永磁電機的工作原理，相關工作人員將電機運行過程劃分為異步啟動階段以及同步階段，本次研究使用的電機型號為MZ060C交流伺服電機，由GSK公司生產，被安裝于RB08串聯型機械臂上，為機械臂的關節活動提供動能。該型號電機外形緊湊，采用全封閉結構，運行過程中電機運轉平穩且電磁噪聲較低。因為電機內的永磁體采用的是高性能稀土，所以該電機具有強大的過載能力，在低速狀態下仍能保持穩定工作。此外，該電機配備了高精度編碼設備，能夠與驅動裝置緊密配合，加之采用進口軸承，有效提升了電機轉子的旋轉精度。

從設備結構方面來看，該電機主要由轉子、定子、端蓋等零件構成，其定子的結構與傳統感應電機的定子結構類似；最重要的區別在于轉子結構，永磁同步電機中的轉子會根據永磁體的位置，按照貼面式、內嵌式、插入式等方式布置。

與傳統的異步電機相比，永磁電機內部結構更為緊湊、可靠性更高，具有較高的運行效率，且電機內部零件的布局較為靈活，能夠根據實際情況進行定制或者調整。目前，永磁電機在航天、工業生產、農業生產等領域均得到了廣泛的應用，并取得了不錯的效果[2]。

2 基于靜止坐標構建永磁電機模型

永磁電機通電之后，在電樞磁場的作用下開始切割定子繞組，通過這種方式在電機內部制造感應電動勢，同時以電磁力驅動轉子旋轉，為機械臂的運行提供動能，其二極面PMSM結構如圖1所示。

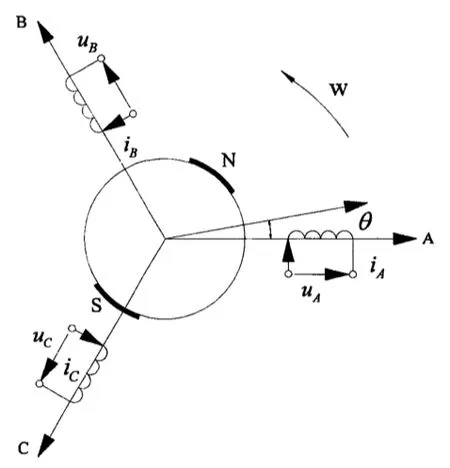
圖1 永磁電機結構簡圖

通過分析圖1可以發現，每一相繞組電壓以及電流方向均被標記出來，依據電動機的工作原理，電流與電壓方向相同。工作人員將正向電流通過一相繞組時產生的正弦波磁動勢軸線定為繞組軸線，并將A軸作為ABC軸的空間參考坐標，通過這種方式在靜態空間坐標系中定位ABC軸上的線圈，如果感應電動趨勢與電流的方向相反，則將逆時針方向作為電磁轉矩的正方向，并將該方向作為負載轉矩的反方向，以此為基礎構建PMSM模型。在構建模型時，需要對三相靜止坐標和兩相靜止坐標中的PMSM模型進行描述。在三相靜止坐標中，三個軸的位置即定子繞組軸中心所在的位置，相位差角度為120°；兩相靜止坐標中，α軸與a軸位于重合位置，β軸經過逆時針旋轉之后與α軸保持90°夾角；兩相旋轉坐標系中，d軸的位置即轉子的N極位置，當轉子轉動之后，d軸隨之轉動，而q軸沿著逆時針方向轉動，與d軸形成90°夾角。

由于永磁同步電機具有非線性磁化特性，且此類電機還具有飽和效應，其動態模型為微分方程，由于該微分方程的階數較高，想要對該方程進行求解較為困難。針對這一問題，需要對該方程進行簡化，忽略一些次要元素。①將永磁電機可能產生的諧波效忽略不計，假設定子三相繞組完全對稱，并且三相繞組之間的夾角均為120°。②不考慮永磁體非線性不飽和因素，假設各項繞組的電感以及阻值恒定，即Ra=Rb=Rc，La=Lb=Lc。③忽略由于磁滯效應所帶來的損耗[3]。④忽略電機工作頻率以及外界溫度變化對電機可能造成的影響。確保上述條件的情況下，得到三相定子坐標系電壓方程：

3 Park與Clark變換

Clark變換實際上就是三相靜止坐標（abc）與兩相坐標（αβ）之間的相互轉換，如圖2所示。

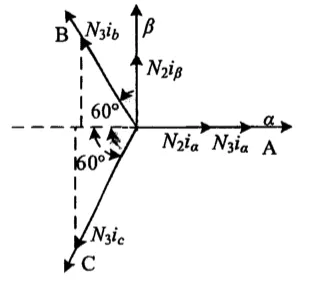
圖2 三相與兩相坐標系繞組磁動勢空間矢量

圖2中，A軸與α軸重合，且三相繞組的匝數為N3，兩相繞組的匝數為N2，其空間矢量位于坐標軸上。由于交流磁動勢為浮動數值，因此磁動勢的矢量長度，需要根據坐標系實際情況確定，如果磁動勢的波形為正弦波，且兩相總磁勢與三相總磁勢相同，則α、β軸上磁動勢的投影相同，得到公式：

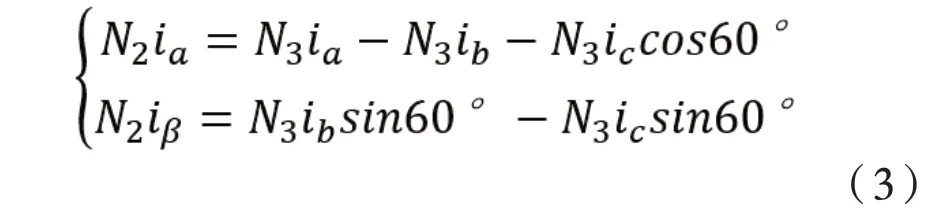
將公式（3）轉變為矩陣，則得到：

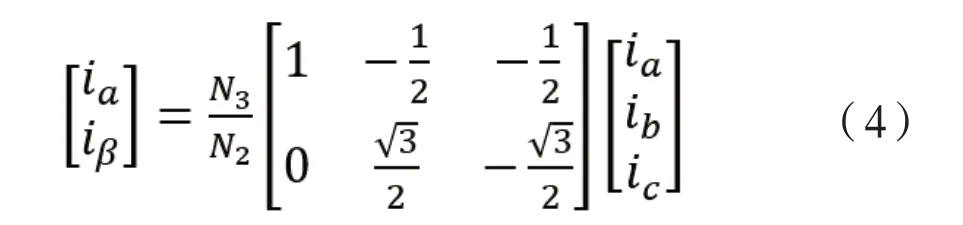
Park變換是兩相靜止坐標與兩相旋轉坐標之間的變換，如圖3所示，該變換中，r表示旋轉，s表示靜止，兩相交流電、與兩相直流電、產生相同的磁動勢Fs，并形成同步旋轉w1。由于三相繞組匝數相等，因此在計算磁動勢時可以忽略匝數，使用電流代指，即=Fs。

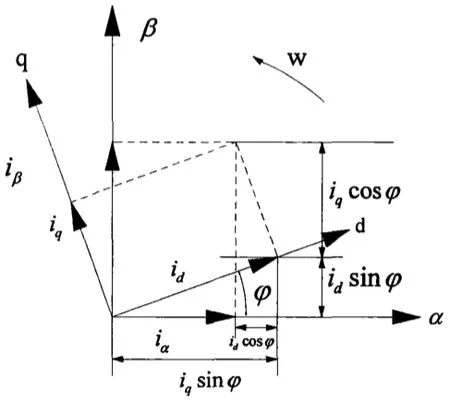
圖3 兩相靜止與旋轉坐標系繞組磁動勢空間矢量

dq坐標與αβ坐標的電流空間矢量計算公式為：

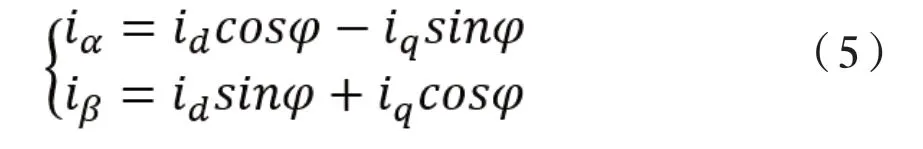
將零軸電流引入公式（5）可以得到矩陣：

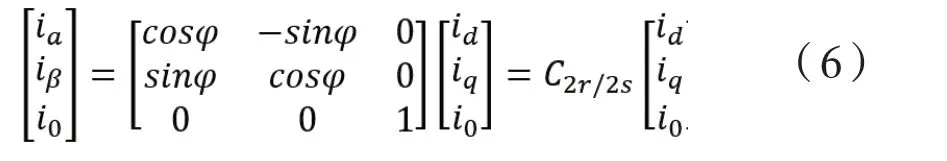
利用Park與Clark變換，能夠得到三相靜止坐標與兩相靜止坐標的變換矩陣，以及兩相靜止坐標與兩相旋轉坐標的變換矩陣，通過等效代換得到三相靜止坐標與兩相旋轉坐標的變換矩陣。

4 基于旋轉坐標永磁電機模型

永磁電機定子的電壓公式為：

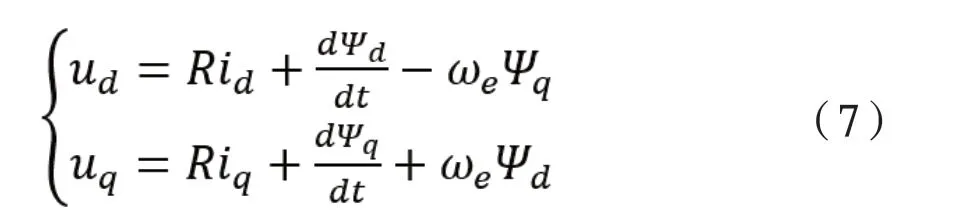
公式（7）中，變量ω表示轉子旋轉的角速度，由于該方程中不包含轉子的位置角數據，則轉子位置角的解耦得以實現，并且對該公式進行了簡化。

電磁轉矩的計算公式為：

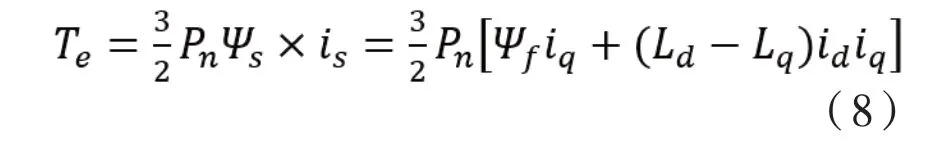
根據上述公式，可以構建基于兩相旋轉坐標的永磁體電機狀態矩陣模型如下：

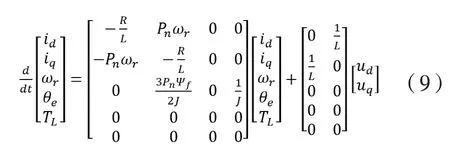
5 矢量控制

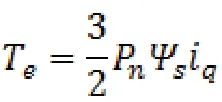
工作人員將給定的電機轉速與實際測得的電機轉速進行對比，利用轉速調節裝置（ASR）得到轉矩的電流分量以及參考量，并給定電流勵磁分量，利用Clark變換將三相靜止坐標中的流量矢量變為兩相靜止坐標的電流矢量、，再借助Park變換得到兩相旋轉坐標的電流矢量、，并將其與、進行比較，得到最佳的矢量控制方案。

6 結語

基于靜止坐標以及旋轉坐標構建永磁電機模型，能夠在計算機上模擬電機的實際工作狀態，并提供Park變換以及Clark變換對永磁同步電機電流的轉矩與磁矩解耦，確保二者保持相對獨立的工作狀態，為降低電機損耗、提升機械臂的工作效率奠定數據基礎。