精密跟蹤型望遠鏡適配的快速星圖匹配

劉德龍，楊文波，柳鳴，康喆，李振偉

（中國科學院 國家天文臺長春人造衛星觀測站，吉林 長春 130117）

1 引言

近年來，大氣層外圍的衛星、空間碎片、火箭箭體和載荷等人造物體不斷增加，空間環境不斷惡化，嚴重威脅了航天器的正常運行，為此需要對目標進行精密定軌、編目、預報及特征分析。基于地基望遠鏡的光電觀測目前仍是最有效的空間目標研究手段之一，它具有觀測軌道高度廣、組網成本低、無接觸及免干擾等優勢。其中，精密跟蹤型望遠鏡通過較長弧段觀測，取得已知軌道目標的定位數據，為其精密定軌服務［1］。天文定位基于背景恒星的絕對位置克服了軸系定位中機械誤差、脫靶量測量誤差和坐標系轉換等帶來的影響，可顯著提高空間目標的定位精度。

星圖匹配是天文定位中不可或缺的一環，它將觀測圖像中恒星的攝影坐標和標準星表中的天球坐標關聯起來，以此解算觀測系統的底片模型。星圖匹配主要依靠子圖同構［2-3］和模式識別［4-5］。子圖同構中的三角形相似算法仍是至今使用最廣泛和有效的星圖匹配算法，然而傳統算法由于特征維數較低，并且需遍歷所有星象，導致匹配效率低，導致既耗時又浪費存儲空間［6］。隨著望遠鏡光學口徑和視場的不斷增大，視場中的星象呈指數級增加。同時天文相機技術也不斷進步，越來越多望遠鏡配備了高幀頻、高分辨率的科學級CMOS相機。這導致在一個觀測周期內圖像序列的幀數和每幀數據急劇增加，進一步凸顯了傳統三角形匹配算法的不足。近年來見諸報道的一些改進算法包括：2019年王軍等人［7］采用三角形外接圓和內切圓半徑乘積作為匹配特征，初步篩選后再進行三角形三邊匹配，2020年劉先一［8］采用徑向特征量縮小了待匹配導航星數量，增強了匹配的針對性；2021年李變等人［9］公開的發明專利提出基礎三角形的概念，預篩選觀測三角形，降低了匹配量；2021年徐偉等人［10］選擇觀測星中星等最小的三顆組成特征三角形，后采用三邊組合特征值的方式進行導航星表的遍歷匹配；2021年熊琨等人［11］的專利也提出縮減導航星，并建立導航星角距庫的思想。這些算法增加了星表或觀測星預處理的復雜度，提高了計算成本；前期預選還有可能造成匹配失敗，因此不滿足序列圖像的首幀星圖匹配中容易實現和成功率高的要求。

精密跟蹤（簡稱精跟）型望遠鏡具有高精度的控制伺服和較大的相機靶面。其圖像序列的特點首先是目標和背景恒星的相對運動，由于望遠鏡跟蹤目標，恒星星象會出現拉長。因此需使用短曝光或采用星象模糊還原算法，前者增加了圖像噪聲，后者使得提取位置發生改變。這均需要匹配算法對于不同天區、軌道和類型的目標具有一定魯棒性，能夠自動選取誤差容限進行運算；第二，碼盤可在拍攝圖像的同時獲取望遠鏡指向，即圖像中心的軸系定位。該指向較為粗略，但可用于定位星表。同一觀測圈次內序列圖像幀間的指向改變量非常精準，可用于快速匹配；第三，望遠鏡指向連續變化，并且幀間變化較小。因此相鄰幀的底片常數變化很小，可用上幀常數進行匹配，之后通過匹配更新底片常數；第四，相對于固定方向觀測，精跟型望遠鏡在觀測周期內動作范圍較大，因此分區指向模型可能會造成結果誤差的不連續。基于以上特點本文提出一種專門適配的星圖匹配算法。

2 星圖匹配模型

望遠鏡電控系統根據引導數據驅動跟蹤，同時采集圖像。后經圖像處理和目標識別給出目標和背景恒星的位置。對于精跟型望遠鏡較小的視場（＜2.5°），六參數模型即可完成匹配。

由于拍攝圖像和實際星圖只存在比例、平移、旋轉或鏡像關系［12-13］，只需要3個對應點，就可以確定底片常數。首先采用三點擬合計算圖像中心對應的天球坐標(α0，δ0)，利用該點的天球坐標計算得到導航星的理想坐標，即(αi，δi)到(ζi，ηi)：

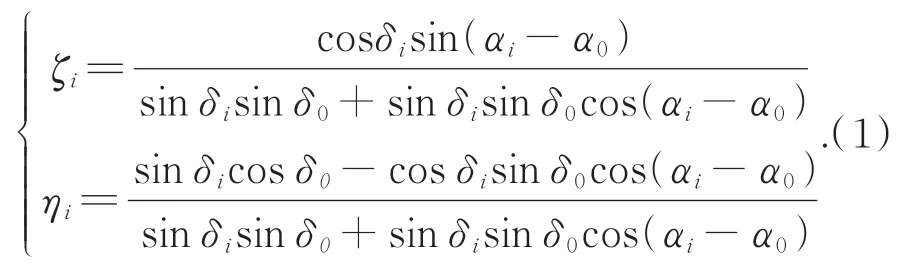
理想坐標實際上是空間星象的地心投影（Gnomonic Projection），其本質是針孔相機的成像關系，即帶入較小畸變誤差地模擬長焦望遠鏡。理想坐標將天球系統轉化為笛卡爾平面坐標，得出了導航星在各幀不同的位置坐標。目標定位時，將其理想坐標(ζs，ηs)轉換為天球坐標(αs，δs)的變換如式（2）：

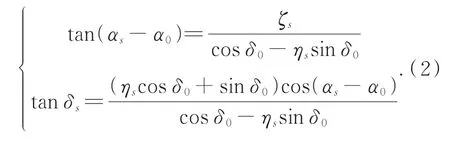
僅依靠3個點可能出現誤匹配的情況，此外三點擬合精度也較低，因此必須對考察列表進行校驗，并進行多點擬合。對于正確匹配，當圖像x和y方向的比例尺相同時，恒星的理想坐標(ζi，ηi)和其度量坐標(xi，yi)應滿足底片常數的對應關系，如公式（3）（當拍攝圖像為鏡像時，轉換矩陣元素應為相應的下組符號）。通過該組關系可以判定匹配是否正確（T是否為酉矩陣［14］），并且將6底片常數減為3底片常數（a，b，θ）：

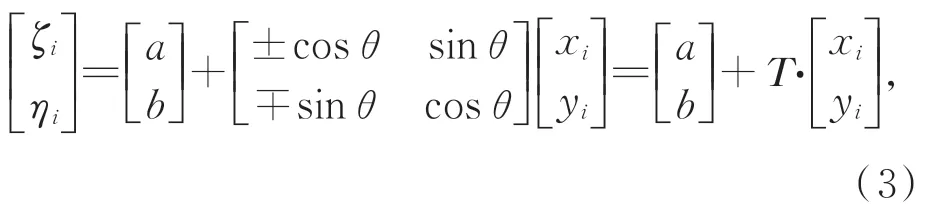
式中：a，b表示理想坐標系和度量坐標系間的平移量，θ表示兩坐標系間的夾角。當已知一組(xi，yi)和其對應的(ζi，ηi)時，底片常數便可由最小二乘法得出。

3 算法構成

3.1 圖像獲取與預處理

本研究工作所有實際觀測都依托于中國科學院國家天文臺長春人造衛星觀測站運維的1.2米口徑地平式光電望遠鏡的主焦點［15］。該望遠鏡位于吉林省吉林市（圖1）。望遠鏡動態峰值誤差為方位軸：2.555″，高度軸：2.170″，為典型的精跟型望遠鏡。望遠鏡搭載的相機為Andor iKon-XL 230，4 096×4 108 pixel，像 素 尺 寸 為15 μm，視 場 約 為1.5°。望 遠 鏡 的 焦 距 約 為2.2 m。

圖1 1.2米光電望遠鏡實物照片Fig.1 Photo of 1.2 m optical telescope of Changchun observatory

拍攝得到的圖像如圖2，應用SExtractor（Source-Extractor）軟 件［16］進 行 星 象 質 心 位置的提取。之后采用靜態特征和運動特征差異來初選疑似目標并通過連續幀關聯確定目標。最后根據望遠鏡指向篩選Tycho-2星表，剔除雙星并選出視星等介于8～10、自行小于10 mas/yr的恒星進行匹配。

圖2 1.2米光電望遠鏡跟蹤目標時拍攝的星空Fig.2 Image captured by the 1.2 m optical telescope when tracking a target

3.2 星表數據的資料歸算

本研究采用Tycho-2恒星星表，該星表是建立于ICRS下的，歷元為J2000.0。因此需將星表中的恒星坐標進行自行、周年視差、周年光行差和光線偏轉的歸算，解算到恒星在觀測時刻的GCRS坐標進行星圖匹配。本文應用ANCI C版本的SOFA（Standards Of Fundamental Astronomy，from IAU）軟 件 包［17］中 的 程 序 做 以 上 的換算。

幾點說明：基于望遠鏡拍攝圖像的天文定位給出的是目標的站心空固坐標，由于恒星站心和地心間的周日視差可忽略，可采用恒星的GCRS坐標進行星圖匹配。恒星由歲差—章動、極移引起視位置差別很小，不影響理論與觀測星圖的匹配。大氣折射同時影響背景恒星和目標，精跟型觀測中該較差可被忽略。

3.3 優化三角形匹配算法

本程序包括兩部分算法：優化三角形匹配和序列圖像修正。優化三角形匹配算法通過降維查表的方法提高運算速度，得到首幀的底片常數和較為精確的中心位置；該中心位置疊加碼盤獲得的望遠鏡指向改變量獲得相應幀底片中心位置，并結合上一幀的底片常數進行新一輪的匹配。流程可見圖3。底片常數可用來解算各像素對應的天球坐標。

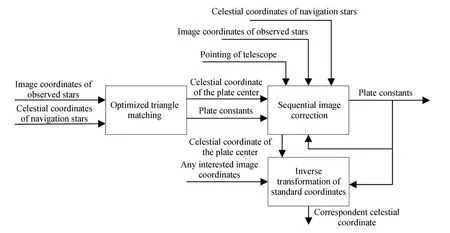
圖3 本文所述快速星圖匹配算法的程序框圖Fig.3 Block diagram of the rapid star pattern recognition algorithm described in this work

本研究中三角形匹配算法利用“邊-邊-邊”模式匹配觀測星和導航星（如圖4所示）。但是傳統算法特征維數較低并且組構三角形過多，造成計算大量的冗余匹配，浪費計算時間和存儲空間。

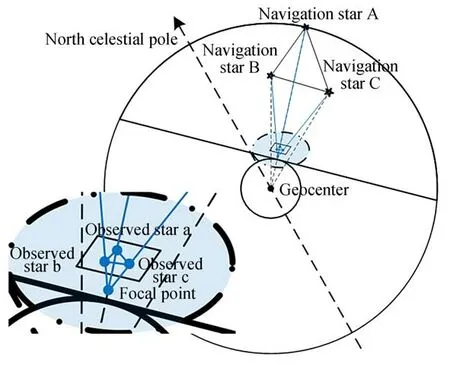
圖4 三角形匹配的模擬示意圖Fig.4 Simulation diagram of triangle matching

優化三角形匹配算法活動圖如圖5所示，觀測端編號并計算每兩顆星象之間的“邊”——角距［18］，按照自然編號的順序存儲。經歸算后星表中的導航星，編號并計算兩兩之間的角距，按照角距大小排列存儲，稱為排序導航星表。具有相同觀測星的兩個星對（例如觀測星對：i，j和i，k），即為待測觀測星對，分別放縮一定的誤差σ后劃取排序導航星表中的兩個片段。判斷這兩個片段內是否存在共享導航星的兩個星對，如果存在（例如導航星對：A，B和A，C），即為待選導航星對，計算這兩個導航星對中不同導航星（即導航星B，C）間的角距。哈希查表（哈希函數如式（4），其中N為篩選星表中導航星數目）得到觀測星對兩相異星角距（即j，k之間角距），放縮該誤差后所劃定的導航星表范圍，判斷該范圍是否包括對應相異導航星（即導航星B，C）的角距。是就將這些觀測星和導航星按照對應關系放入待考察列表中（即i，j，k對應A，B，C）：

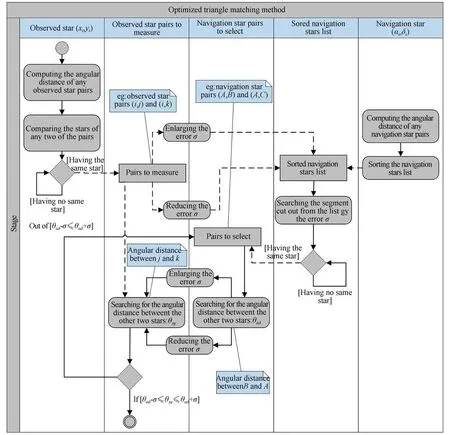
圖5 優化的三角形匹配算法的活動圖Fig.5 Activity diagram of the optimized triangle matching algorithm

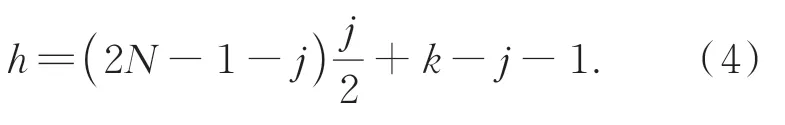
完成一組匹配后即得到粗略的定位關系，可求得圖像中心對應的天球位置。該位置用來求得導航星的理想坐標，并將這組匹配進行參數擬合得到底片常數。用式（2）驗證該底片常數，滿足校驗關系后進行觀測星和導航星間的匹配，當有足夠多匹配時，該底片常數方為正確。當無法得到正確匹配時，需要放大誤差再次進行匹配，直到得到正確匹配或誤差不可接受為止。放大誤差后，導航星表范圍增加，需屏蔽已考察的列表片段避免重復匹配，提高匹配效率。

3.4 序列圖像修正算法

地心投影通過各幀圖像中心將導航星絕對的天球坐標投影為本幀理想坐標；對于較高幀頻的精跟型望遠鏡，幀間的底片常數變化很小，因此本幀理想坐標和上一幀參數可完成匹配。但是為了不引入累積誤差，完成匹配后還需再一次的多點擬合修正底片常數。序列圖像修正算法在不損失精度的前提下點對點地完成匹配，極大地節約存儲空間，提高計算速度，這對于實時性解析目標位置有著重要意義。除此之外，對于大視場的望遠系統，較多的背景恒星會造成三角形匹配中內存消耗過大、效率過低，對此可以根據望遠鏡指向篩選導航星并劃取圖像中心區域的觀測星進行優化三角形匹配，再將得出的底片常數應用序列圖像修正算法推廣到整幀圖像，進行底片常數計算。需要注意的是，這種情況下，常采用十二參數模型進行匹配，可以在一定程度上克服相機圖像的畸變。序列圖像修正算法流程如圖6所示。

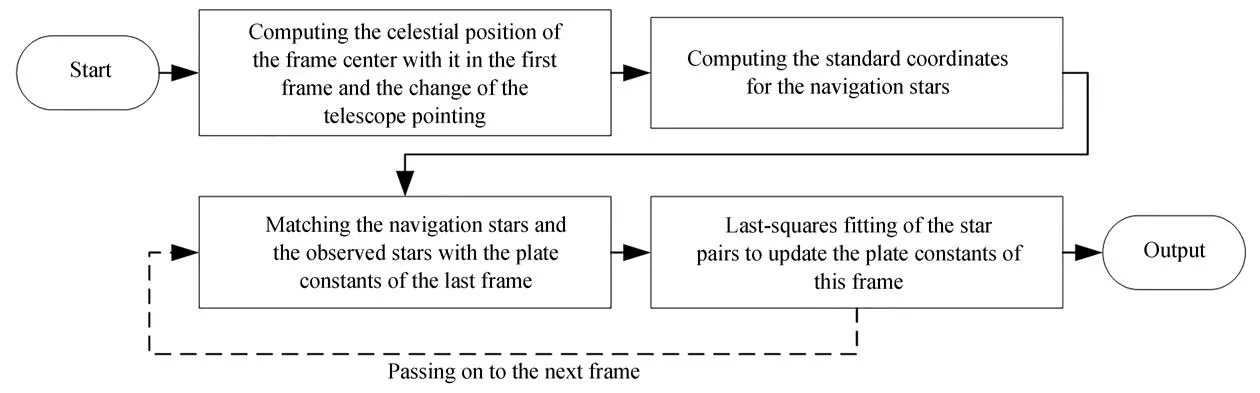
圖6 序列圖像修正算法流程圖Fig.6 Flow chart of sequential image correction algorithm

望遠鏡碼盤給出了其中心指向，但一些原因，如自然條件、熱脹冷縮、配重變化、重力變形、結構改變（本例中望遠鏡可以調節主焦點和卡塞格林焦點）等會造成該指向不準；然而在同一圈次的觀測中，指向的相對精度較高，因此配合首幀的修正中心就可以大幅提高底片的中心位置精度。該中心位置對恒星理想坐標運算和目標位置解算有著重要意義，同時還可對望遠鏡指向偏差提供參考。

4 實驗結果

本研究采用Windows系統的計算平臺，CPU：AMD Ryzen 5@3.4 GHz，內 存：8 GB DDR4，編譯環境為VS 2019。

將優化算法和傳統的三角形匹配算法作比較，對于39顆觀測星對應39顆導航星的實驗，傳統算法耗時2.105 s，而優化算法耗時0.044 s。

將算法應用于精跟測試中軌激光星的事后分析中，觀測時間為2019年4月，指向范圍：（1 h30 m16.2 s，53°0′50.2″）～（2 h15 m13.0 s，50°33′40.0″）。首幀識別到326顆觀測星，篩選出66顆導航星，首先對所有涉及的背景恒星進行了歸算，共消耗時間0.005 s，后采用優化的三角形匹配算法對首幀數據進行匹配。經4次放大，理想坐標匹配誤差為0.000 04時，可匹配60對星象，共需時間0.75 s。經最小二乘法擬合出底片和地平取向基本成鏡像。匹配結果如圖7，其中紅圈表示成功匹配的星象（彩圖見期刊電子版）。

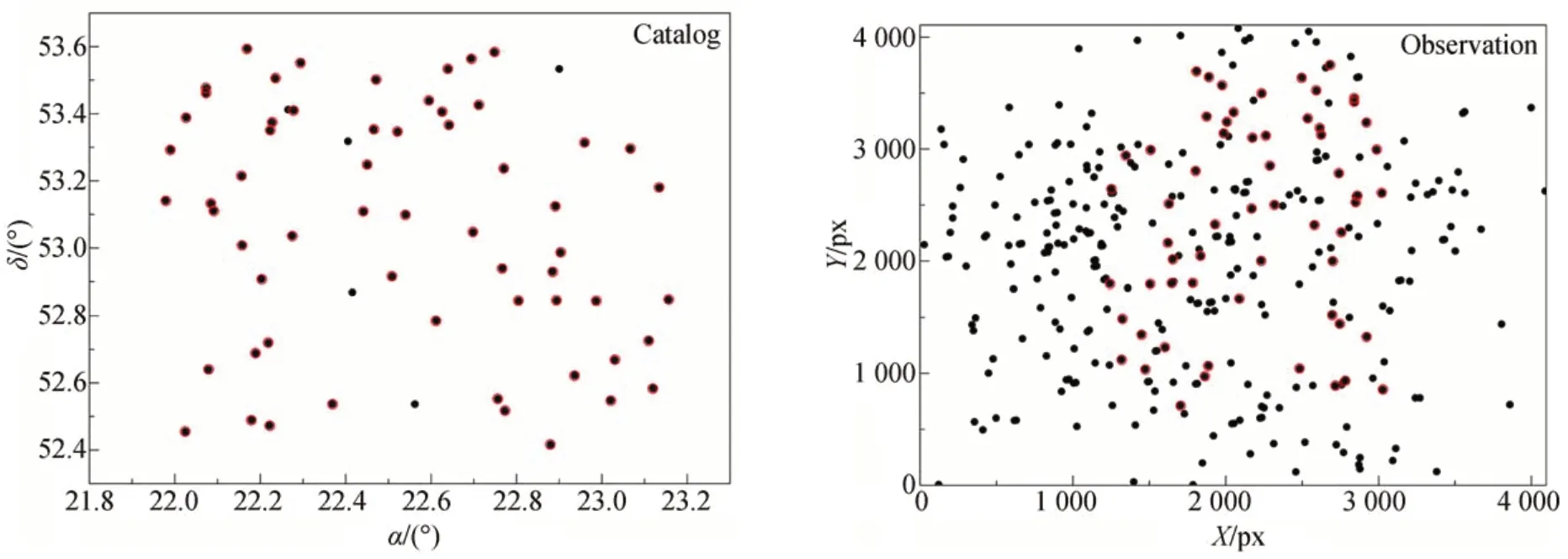
圖7 觀測星和導航星二維點圖Fig.7 Two dimensional point maps of observation and navigation stars

對后續幀采用序列圖像修正算法，將計算結果列于表1，可見該算法耗時均在0.04 s以內，在識別到充分多觀測星時，可實現絕大多數導航星的匹配。

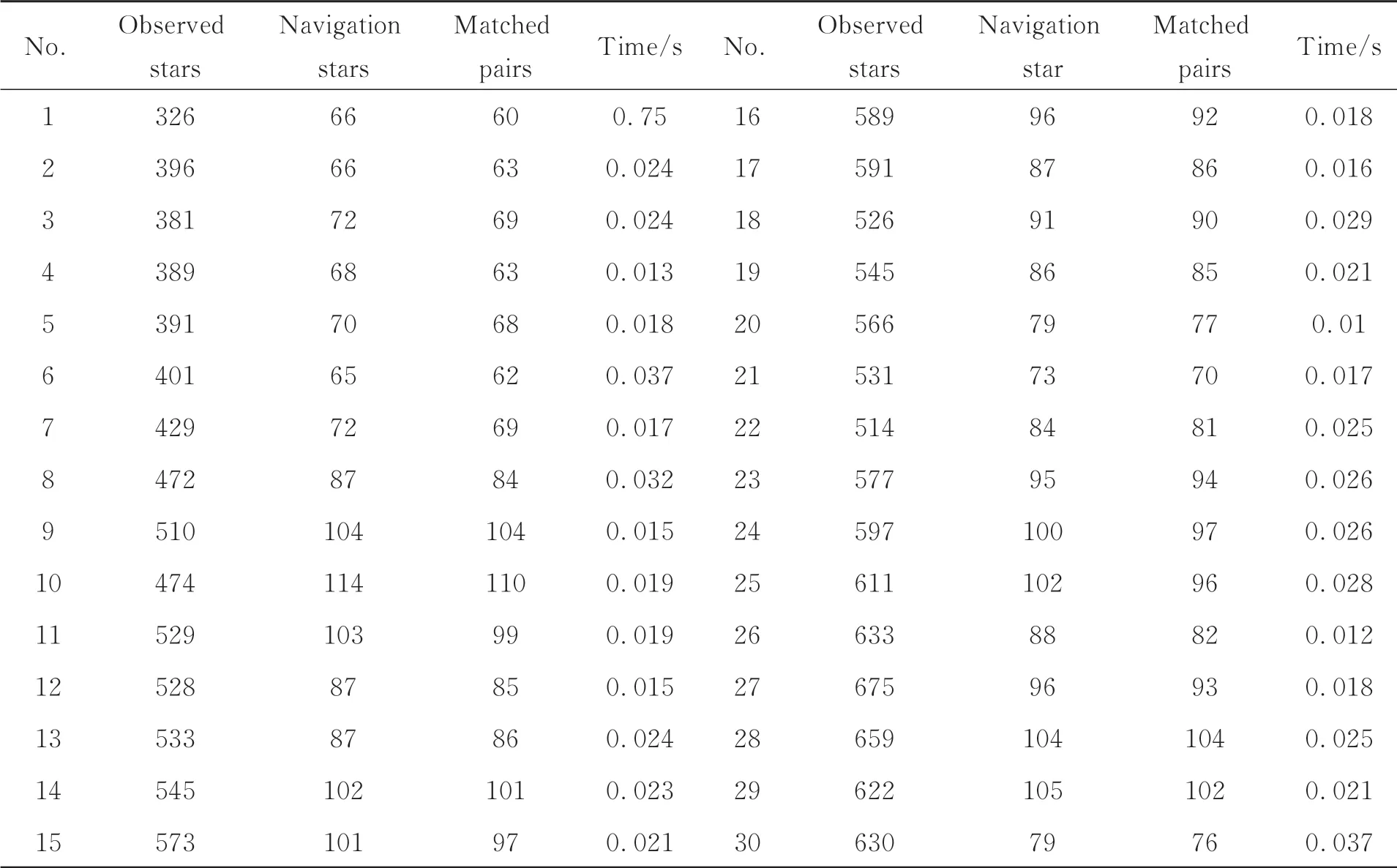
表1 序列星圖匹配結果Tab.1 Results of sequential star pattern matching

匹配星對用于擬合，得出各幀的底片常數。底片常數的緩變是序列星圖匹配算法的主要依據，30幀的常數（式（3）中a和b）變化如圖8所示，可見常數變化較為均勻，可用線性回歸來表示，其皮爾森相關系數均達到99.6%以上；并且經30幀，兩參數均減小了不超過10%。

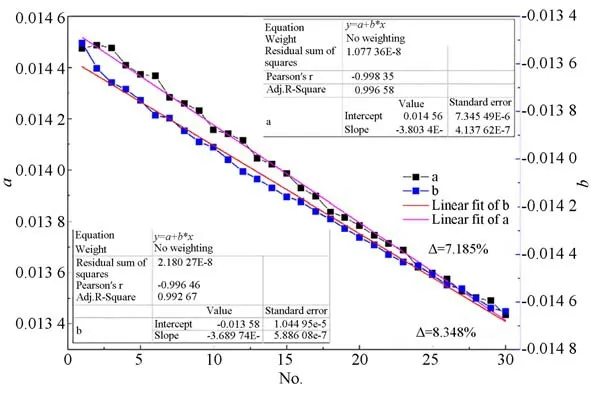
圖8 序列星圖匹配算法中底片常數a和b的變化Fig.8 Changes in the constants a and b in the sequential star pattern matching

由擬合的底片常數計算得出的觀測星的天球位置和實際導航星之間的誤差可由圖9表示（彩圖見期刊電子版），某一典型幀赤緯方向的誤差由綠色球表示，赤經方向由紅色方塊表示。可見除個別邊緣點外，絕大多數的星象誤差在6角秒以內。由于精跟型拍攝目標多位于視場中心，其誤差會進一步縮小，對于觀測的中軌激光星，30幀的目標統計誤差如圖10所示。可以看出，除第一幀以外，絕大部分目標的誤差在2″以內，所有幀的平均誤差為=0.53''，=-0.34''。由此可證明本文所述方法的有效性。

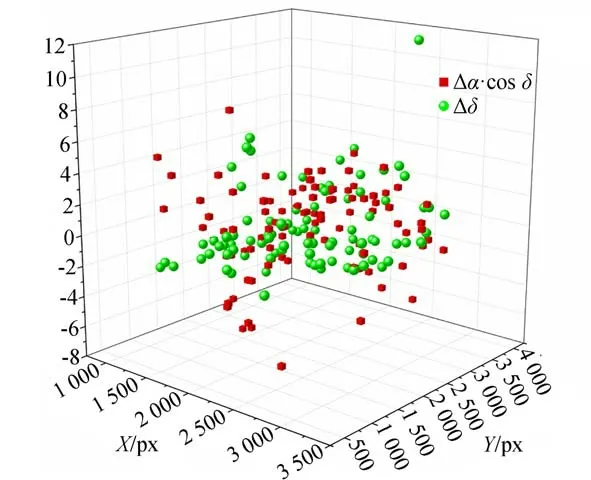
圖9 某幀星圖匹配采用底片常數計算觀測星的天球位置和導航星的誤差分析Fig.9 Error analysis of the celestial positions of the observation stars within the film constants calculation and the respondent navigation stars

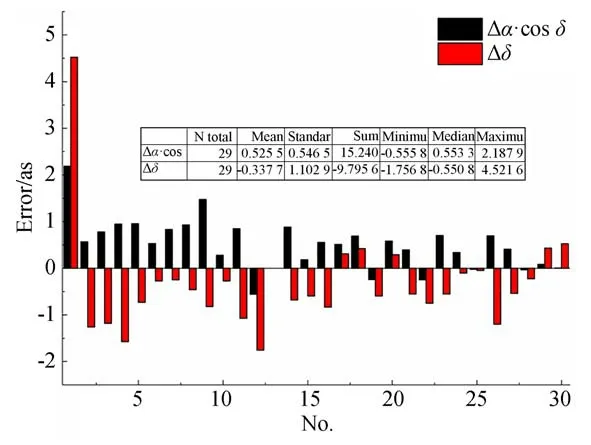
圖10 30幀星圖匹配用于目標天文定位的誤差統計Fig.10 Error statistics of star pattern matching for the target celestial positioning in 30 frames

5 結論

本文所述的星圖匹配程序包括基于降維查表優化的三角形匹配和基于上一幀底片常數的序列圖像修正，該程序特別適用于精密跟蹤型的大視場望遠鏡。其中優化三角形匹配算法相較于原始算法大幅提高了匹配速度（39顆觀測星對應39顆導航星，時間從2.105 s降到0.044 s），而序列圖像底片常數修正進一步加速，使得100顆左右的匹配星對在0.04 s以內完成，這說明了算法的高效性；本方法對中軌激光星定位的結果顯示其平均誤差為