組合折腹梁橋外包型結合部受力機理分析

王思豪張 云張坤球劉玉擎，*

（1.同濟大學橋梁工程系，上海 200092；2.廣西北投公路建設投資集團有限公司，南寧 530007；3.廣西路建工程集團有限公司，南寧 530007）

0 引言

組合折腹橋梁中折形鋼腹板與混凝土頂底板的連接是該種橋梁最重要的構造之一［1］。對于折形鋼腹板與底板的連接，當前普遍采用翼緣型和嵌入型，但兩種方式均存在不足：翼緣型結合部下翼緣板設置焊釘或開孔板連接件，鋼翼緣板下的混凝土逆向澆筑，混凝土的密實性難以保證，連接件抗剪性能降低；嵌入型結合部腹板直接插入混凝土底板中，由于折形腹板縱向剛度小，折形鋼腹板與混凝土底板結合面易出現分離，必須采取防水等耐久性措施。

為解決上述傳統連接方式的不足，德國Altwipfergrund橋［2］首次采用外包型結合部，如圖1所示，下翼緣鋼板和折形鋼腹板緊貼底板外側表面包裹住底板，同時在腹板側面和下翼緣鋼板上部布置焊釘或開孔板連接件。外包型結合部具有良好的耐久性和施工便宜性，施工時下翼緣板直接支撐在底模上，無需臨時支撐，方便折形鋼腹板定位；底板混凝土直接自上而下澆筑，澆筑質量易保證，有利于提高連接件的抗剪性能；鋼混結合面位于箱梁內部，無須擔心界面滲水等耐久性問題；下翼緣板上可直接鋪設預制底板，有利于該種橋梁的預制裝配化施工。近年來該種結合部在新建的組合折腹橋梁中得到積極應用，如日本杉谷川橋［3］、杭州德勝路高架橋［4］、運寶黃河大橋［5］、廣西飛龍大橋等。

圖1 外包型結合部應用實例Fig.1 Practical applications of partial encased connection

雖然外包型結合部已在國內外多座橋梁中得到應用，但關于該種結合部力學性能的研究很少。高渕［3］介紹了日本杉谷川橋外包型結合部構造及預制底板施工方法；王梟等［5］介紹了運寶黃河大橋底板外包型結合部的設計構造。Wang等［6］通過開展推出試驗和非線性有限元模擬探究了采用開孔板連接件的外包型結合部抗剪性能，提出了結合部種開孔板的抗剪承載力計算公式。

外包型結合部中連接件受力機理是結合部設計的重要依據，然而當前尚未有相關研究。為此，本文以采用外包型結合部的懸臂梁為研究對象，通過有限元方法研究結合部連接件受力規律，比較腹板類型對連接件受力的影響，提出外包型結合部連接件單位長度剪力計算方法，為組合折腹梁橋腹板與底板結合部設計提供參考。

1 有限元模型

如圖2所示，以長度30.2 m的懸臂梁為研究對象，采用ANSYS軟件建立其三維實體-板殼混合有限元模型。其中混凝土采用SOLID65單元模擬，鋼板采用SHELL181單元模擬。上翼緣板和頂板建立耦合約束關系，不考慮二者的相對滑移。外包型結合部焊釘連接件采用COMBIN14彈簧單元模擬，賦予彈簧單元三向剛度，焊釘的抗剪剛度和抗拉拔剛度分別參考文獻［7］和文獻［8］取值。采用CONTAC173和TARGE170單元在下翼緣板和底板、腹板和底板之間建立接觸對。混凝土采用C50，鋼材采用Q345qD，荷載僅考慮懸臂梁的自重效應。

圖2 有限元模型Fig.2 Finite element model

為驗證上述建模方法的合理性，首先以一根30.2 m組合T梁為研究對象，不考慮自重效應，在自由端施加1000 kN集中力，計算得到單位長度連接件剪力q，與文獻［9］中理論計算結果進行對比分析。懸臂T梁構造尺寸和計算結果如圖3所示。不考慮懸臂根部和加載端由于邊界和集中荷載影響導致的連接件剪力不規律，有限元和理論計算結果比值均值為0.994。因此，有限元模擬方法可以準確計算連接件的受力。

圖3 有限元模型驗證Fig.3 Validation of finite element model

圖4 為擬定的組合折腹梁橫截面和結合部構造尺寸。截面采用單箱單室，梁高3.5 m；頂板寬10 m，跨中厚度30 cm；腹板中心間距5 m，底板厚30 cm。腹板分別采用平鋼腹板和折形鋼腹板兩種構造，板厚16 mm。折形鋼腹板采用標準1600型波，共包括19個標準波形，從根部至自由端依次編號為1～19。外包型結合部中腹板上設置4排焊釘，每個子板段布置2列，豎向間距120 mm，橫向間距200 mm；翼緣板上布置兩排焊釘，縱向位置與腹板焊釘一致，橫向間距120 mm。焊釘直徑22 mm，高度150 mm。

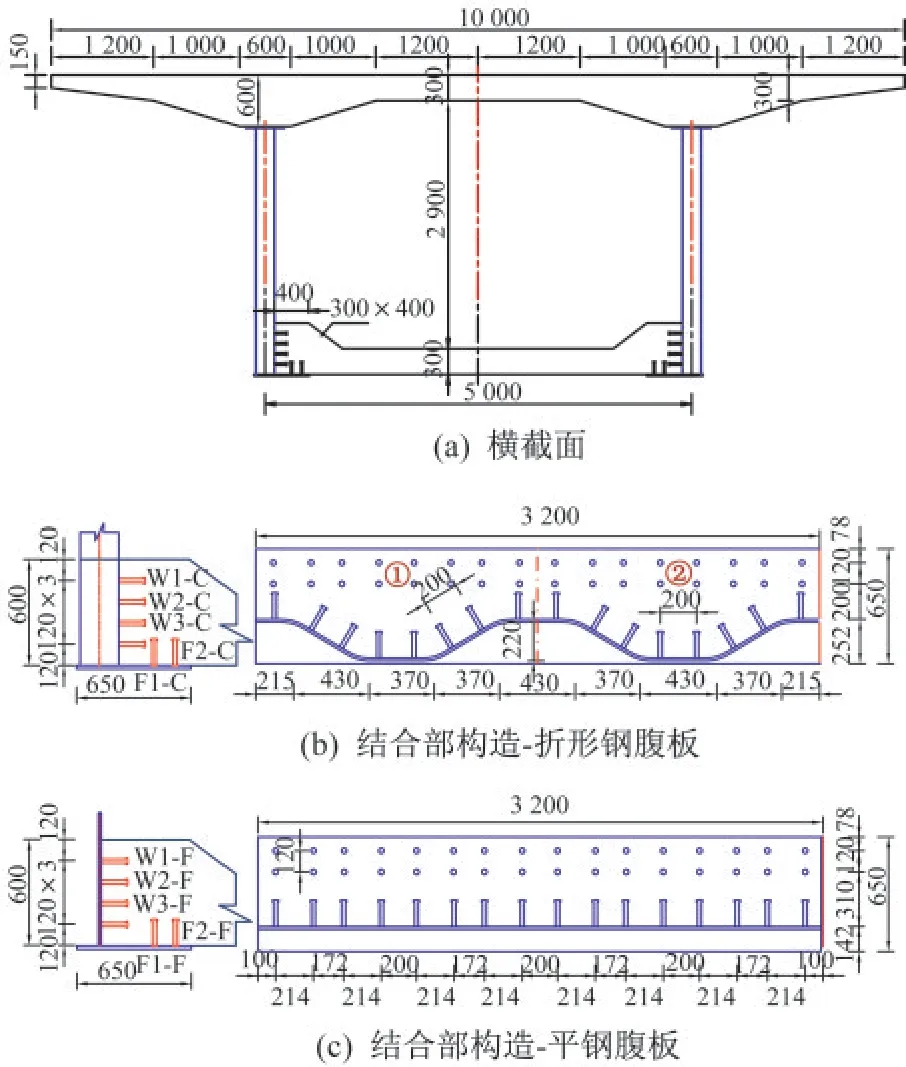
圖4 橫截面和結合部構造尺寸（mm）Fig.4 Configuration of cross-section and connection

2 外包型結合部變形分析

圖5為外包型結合部兩標準波段鋼混相對變形圖，變形量放大1000倍。定義單個標準波段內懸臂根部一側斜板為A類斜板，自由端側斜板為B類斜板，靠近箱室外側直板為外凸直板，靠近箱室內側直板為內凹直板。

圖5 外包型結合部鋼混相對變形示意Fig.5 Relative deformation between steel and concrete of partial encased connection

混凝土底板相對折形鋼腹板產生向懸臂自由端方向的滑移，折形鋼腹板的內凹直板段對鋼混之間的相對滑移產生阻擋效應，使得外凸直板及相鄰兩斜板彎折處與混凝土底板產生相對剝離，相對剝離量自底板上表面向下表面呈減小趨勢，內凹的折形鋼腹板直板段與底板混凝土貼合良好。折形鋼腹板和底板之間最大縱向相對滑移為0.241 mm，最大相對剝離為0.193 mm，出現在距離懸臂根部第3個標準波段內。對于平鋼腹板外包結合部，腹板與底板之間存在相對滑移，但二者仍貼合良好。

3 外包型結合部受力分析

3.1 結合部連接件剪力分布

圖6為外包型結合部中首排腹板和翼緣板焊釘剪力沿縱橋向的分布曲線，其他各排焊釘剪力分布規律類似。對于折形鋼腹板組合梁，腹板和翼緣板焊釘剪力從懸臂根部向自由端均呈正弦形波動減小。以一個標準波長（Lw=1.6 m）為循環周期，在一個標準波段內，腹板焊釘剪力差異很大，其中斜板B中焊釘剪力最大，外凸直板和內凹直板剪力次之，斜板A中焊釘剪力最小，最大剪力接近最小值的3倍。內凹直板相鄰兩列焊釘剪力基本相同，而外凸直板中靠近懸臂根部一側焊釘大于靠近自由端一側焊釘剪力。對于采用平鋼腹板的外包型結合部，焊釘剪力從根部向自由端呈線性減小，基本無波動變化。在同一縱向位置處，平鋼腹板焊釘剪力略小于折形鋼腹板外凸直板上焊釘剪力值。

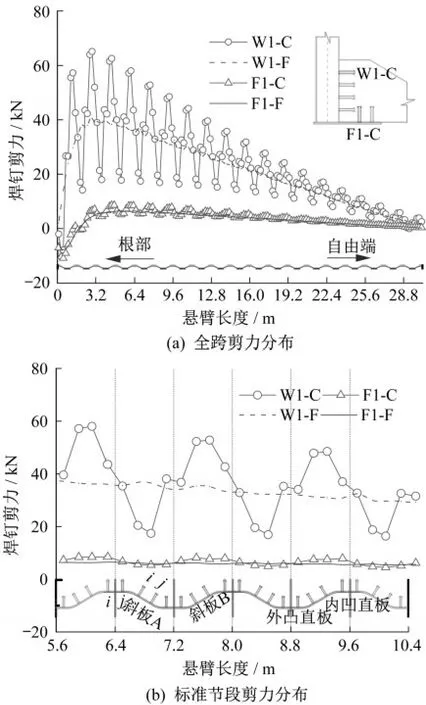
圖6 焊釘剪力縱向分布Fig.6 Horizontal distribution of shear force

折形鋼腹板連接件剪力的波動變化主要是由于腹板彎折形狀導致的，底板與腹板之間的縱向相對滑移受到內凹直板阻擋，使得標準波段內各子板與底板之間相對滑移并不均勻。

圖7為5號標準波段內各子板j列焊釘剪力沿豎向的分布曲線，i列焊釘剪力分布規律相同。對于采用折形鋼腹板或平鋼腹板的外包型結合部，腹板焊釘剪力自上而下均呈逐漸減小趨勢，首排焊釘剪力約為底排焊釘剪力的2.5倍。下翼緣板上兩排焊釘剪力基本相同，且均小于腹板焊釘。

鎮長在村長陪同下來到牛皮糖的病房時，電視開著，牛皮糖卻不在。派人去找，在一個下象棋的人堆里把他請了回來。見到鎮長，牛皮糖鞠了一個躬說，爺，你總算來了。

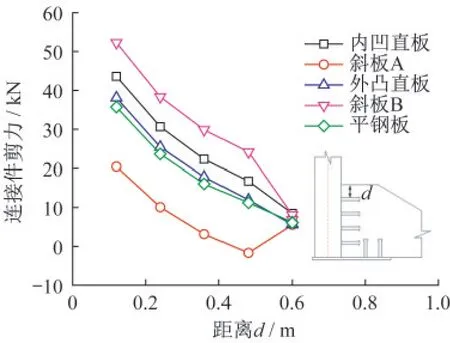
圖7 焊釘剪力豎向分布Fig.7 Vertical distribution of shear force

由于腹板與底板之間的相對滑移自上而下逐漸減小，導致首排焊釘分擔較大的剪力值，翼緣板處于底板下表面，鋼混相對滑移最小。因此，連接件布置時，應重點加強腹板上連接件布置，提高最靠近底板上表面即首排連接件的抗剪承載性能。

3.2 結合部連接件拉拔力分布

圖8為外包型結合部中首排腹板焊釘拉拔力沿縱橋向的分布曲線，其他各排焊釘剪力分布規律類似。對于折形鋼腹板組合梁，從懸臂根部向自由端焊釘剪力呈波動減小趨勢。同樣以一個標準波段為變化周期，在一個標準波段內，出現拉拔力的焊釘主要分布在兩斜板和外凸直板上，內凹直板拉拔力很小，拉拔力最大值出現在斜板A上的j列焊釘。采用平鋼腹板的外包型結合部腹板連接件基本不存在拉拔力。

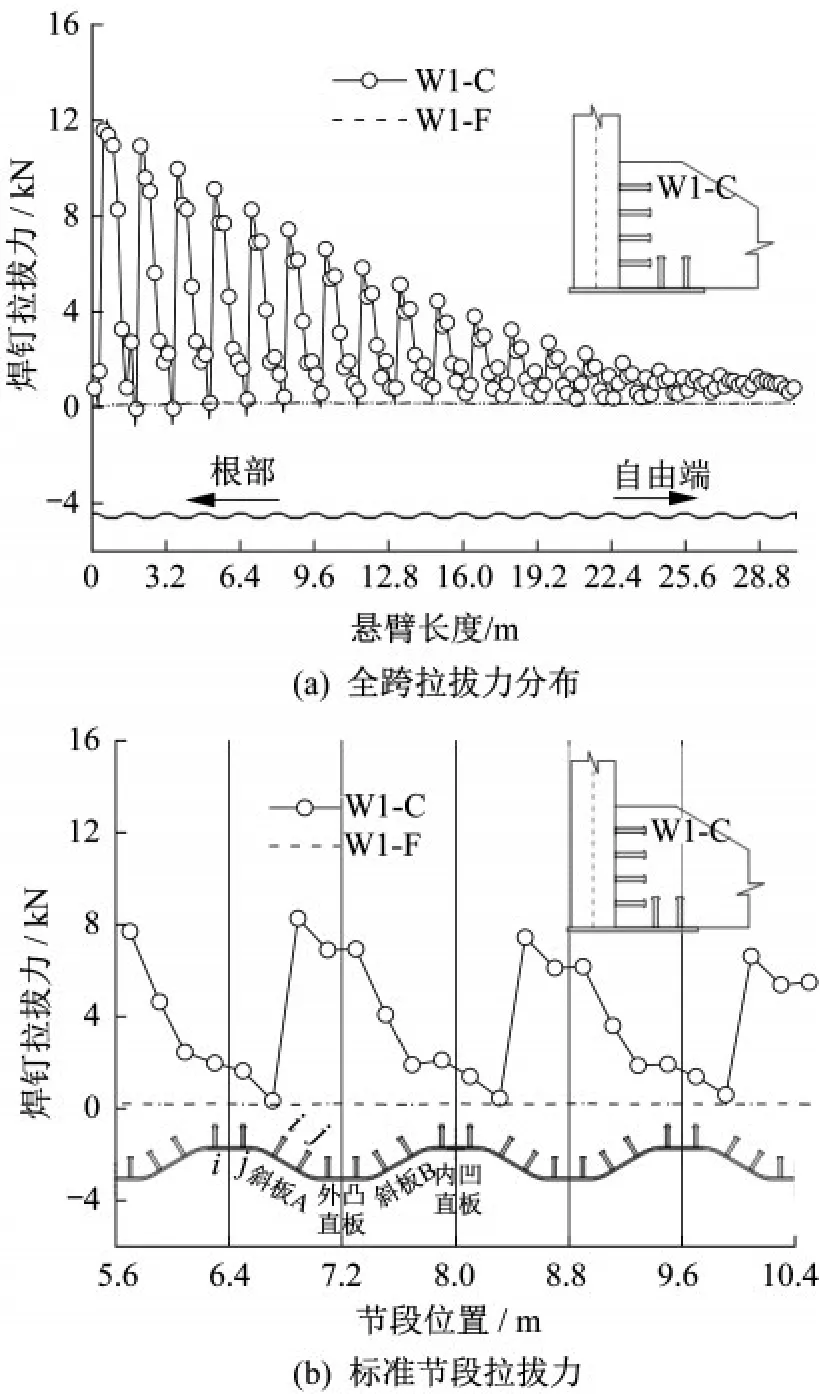
圖8 焊釘拉拔力縱向分布Fig.8 Longitudinal distribution of tensile force

外包型結合部中折形鋼腹板上連接件的拉拔力是由于腹板形狀及鋼混相對變形模式導致的。自重作用下底板相對于折形鋼腹板向懸臂自由端運動，受到內凹直板的阻擋，導致外凸直板和相鄰斜板出現與混凝土的相對分離，相應連接件出現一定拉拔力。

圖9為5號標準波段內各子板j列焊釘拉拔力沿豎向的分布曲線，同一子板的i列焊釘分布規律相同。對于存在拉拔力的各列腹板焊釘，拉拔力大小力自上而下同樣呈減小趨勢，且第二排即W1-C焊釘，相對前一排焊釘拉拔力減小幅度最大，說明焊釘拉拔力仍然主要為首排焊釘承擔，鋼混之間的相對分離自上而下逐漸減小。

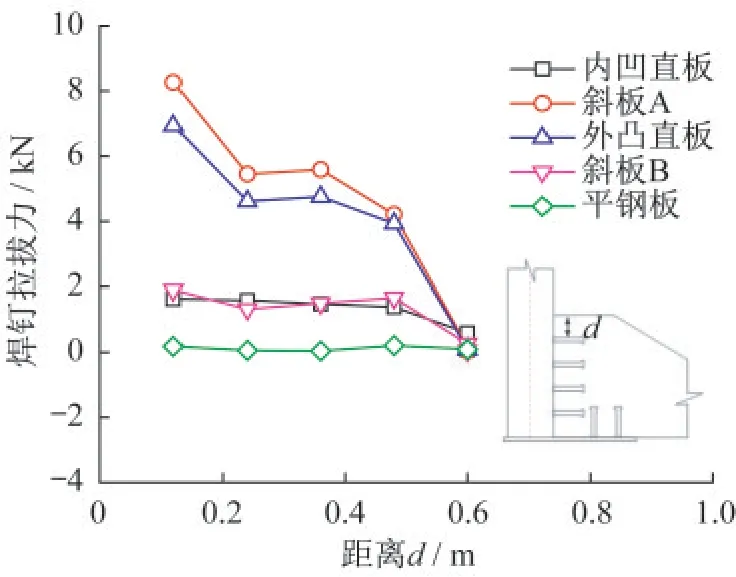
圖9 焊釘拉拔力豎向分布Fig.9 Longitudinal distribution of tensile force

外包結合部中折形鋼腹板首排部分連接件為拉剪受力狀態，實橋連接件布置時宜重點考慮加強首排焊釘。采用焊釘連接件時應保證焊釘的埋入深度和距離底板上表面的最小邊緣距離，保證承載能力極限狀態下為延性拉斷破壞模式，而非焊釘的脆性拔出破壞。

3.3 單位長度連接件剪力合力分布

圖10為各波段范圍內焊釘合力縱向分布曲線。橫坐標為各標準波形中心至懸臂根部距離，縱坐標為該標準波形長度（1.6 m）范圍內連接件的剪力合力。

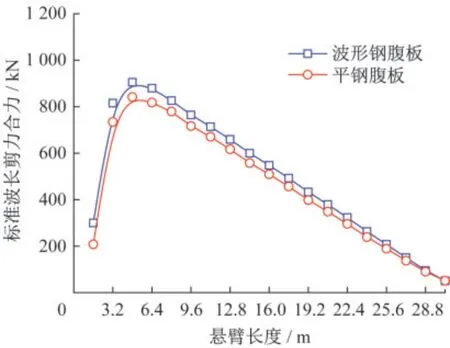
圖10 標準波長剪力合力縱向分布Fig.10 Longitudinal distribution of resultant shear force in a wavelength of corrugation

從3號波形至懸臂自由端，標準波形長度范圍內焊釘剪力合力呈線性減小趨勢，與懸臂梁剪力圖分布趨勢基本相同。對于靠近根部的2個波形，由于邊界條件約束鋼混之間的相對變形，連接件剪力相對較小。為此，在計算組合折腹梁外包結合部中連接件受力時，單位長度應取為標準波形長度Lw，與組合鋼板梁橋結合面連接件剪力計算方法類似，單位長度范圍內連接件剪力合力與組合梁截面豎向剪力成正比。

對于采用平鋼腹板外包型結合部，各標準波形位置處連接件合力均小于折形鋼腹板外包結合部，兩者比值為0.92。主要是由于折形鋼腹板剪切變形大，剪切變形不僅會增大組合梁撓度，同時會增大結合面剪力流，導致折形鋼腹板組合梁結合部連接件剪力相對平鋼腹板增大。

3.4 各子板連接件剪力分擔比

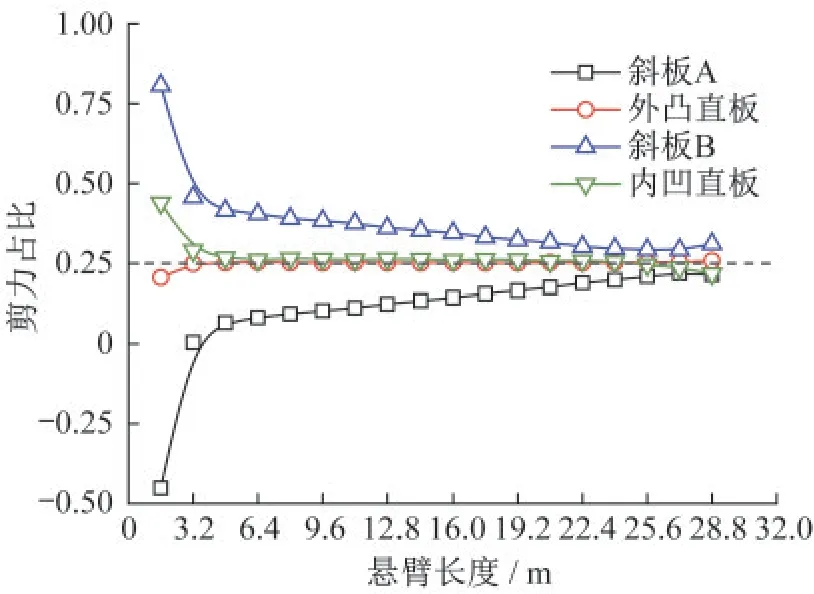
圖11 子板剪力占比縱向分布曲線Fig.11 Longitudinal distribution of shear forceproportion in sub-panels

4 單位長度連接件剪力計算方法

為得到外包結合部中不同位置連接件剪力，首先需要計算單位長度（Lw）范圍內連接件剪力合力。圖12為采用外包型結合部的組合梁簡化計算截面。

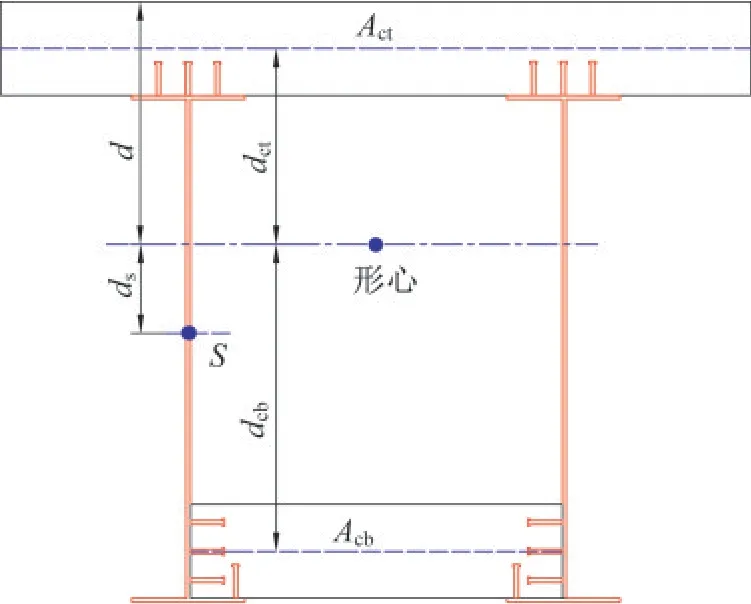
圖12 外包型結合部組合折腹梁簡化截面Fig.12 Simplified section of composite girder withpartial encased connection

參考組合鋼板梁橋結合部焊釘剪力計算方法，結合部上單位長度（Lw）內連接件所需承擔的剪力Vs為單位長度內結合部上的縱向剪力流q，與斷面豎向剪力V成正比。對于折形鋼腹板外包型結合部，考慮剪切變形導致的連接件剪力增大效應，得到折形鋼腹板外包型結合部中鋼混界面單位長度（Lw）上的縱向水平剪力q，如式（1）所示：

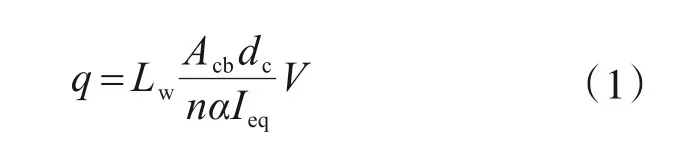
式中：V為計算截面的剪力設計值；Acb為混凝土底板面積；Ieq為換算截面的抗彎慣性矩；n為鋼板和混凝土彈性模量比值；Lw為標準波長；α為連接件剪力增大系數，可取為折形鋼腹板形狀系數，即標準波長與波形展開長度的比值。

圖13對比了外包型結合部單位長度（Lw）剪力合力理論和有限元計算結果。可以看出理論和有限元計算結果吻合良好，公式（1）可以準確計算組合折腹梁外包型結合部單位長度（Lw）剪力大小。實橋結合部連接件設計時，可首先根據該公式得到標準波形范圍連接件剪力，再考慮波形內部剪力的不均勻分布現象，進行不同高度和子板處連接件設計。

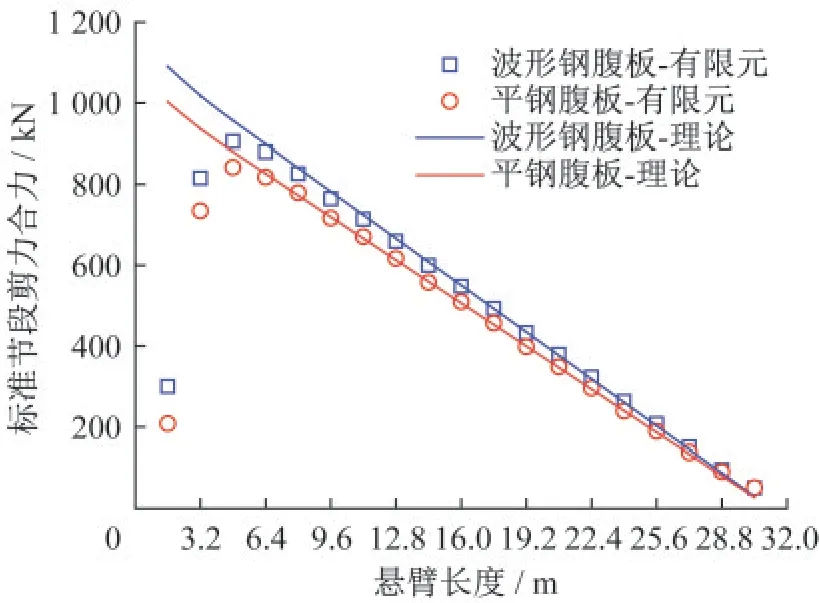
圖13 理論與有限元對比Fig.13 Comparison between theoretical and finite element results

5 結論

通過上述分析，可得出以下結論：

（1）由于波折形狀的影響，外包型結合部一個波段內各子板連接件剪力差異很大。對于組合折腹懸臂梁，一個波段內相同高度處斜板B中連接件剪力最大，外凸直板和內凹直板剪力次之，斜板A中連接件剪力最小。

（2）折形鋼腹板與底板的相對變形受到斜板段阻擋，導致外凸直板和部分斜板與底板存在剝離趨勢，使得部分連接件出現一定拉拔力。

（3）外包結合部中腹板連接件剪力和拉拔力自上而下呈逐漸減小趨勢。下翼緣板處于底板下表面，連接件剪力較小，且不存在拉拔力。因此，實橋連設計時應重點加強腹板首排連接件布置。

（4）在一個標準波形內，內凹和外凸直板各分擔25%的剪力，兩斜板的剪力分擔比存在較大差異，且與該波形所處的位置有關。

（5）考慮剪切變形對剪力的增大效應，得到組合折腹梁外包結合部單位長度連接件剪力計算方法，可初步用于組合折腹梁外包形結合部連接件抗剪設計。