柔性關節復雜遲滯特性的改進WLSSVM建模方法＊

黨選舉 馬樑海

（①桂林電子科技大學電子工程與自動化學院，廣西 桂林 541004；②廣西智能綜合自動化高校重點實驗室，廣西 桂林 541004）

近年來，協作機器人在高端制造、醫療服務、防災抗疫等領域廣泛應用，這對協作機器人的執行精度提出了更高要求。但作為柔性關節核心部件的諧波減速器在動力傳動過程中，由于柔輪受載變形時的彈性變形能量損失，故而柔輪與剛輪齒合時產生摩擦損失，這一固有的機械結構特性致使柔性關節在運動過程中不可避免地出現復雜遲滯特性，嚴重影響協作機器人的位置執行精度[1-2]。因此，為了滿足高精度控制要求，對關節中諧波減速器的遲滯特性進行建模尤為重要。

柔性關節遲滯特性一般指輸出力矩與扭轉角（輸入軸與輸出軸夾角）的關系，具有多值對應、強非線性和非對稱的特點。針對遲滯特性的建模方法中，除傳統的物理模型如Preisach模型[3]、PI模型[4]和Maxwell模型[5]，非線性微分模型如Bouc-Wen模型[6]和Duhem模型[7]，近年來出現具有較高全局優化能力和泛化能力的智能遲滯模型，典型的有采用神經網絡或最小二乘支持向量機（LSSVM）的遲滯建模方法[8-10]等。

智能建模方法中的LSSVM是結合統計學習知識與結構風險最小化理論的一種機器學習算法。與一般的神經網絡對比，LSSVM具有較高的建模速度和泛化能力，常應用于遲滯建模。文獻[11]借助LSSVM對氣動肌肉的位移和氣壓遲滯關系進行建模研究。文獻[12]和[13]基于LSSVM理論對壓電作動器進行建模和控制研究。文獻[9]利用基于非線性自回歸模型結構的LSSVM對構成驅動器的智能復合材料實現遲滯建模與控制。但無論是LSSVM還是基于非線性自回歸模型結構的LSSVM遲滯模型，都用于遲滯特性表現為對稱性、正逆程弱非線性特性的壓電陶瓷或氣動肌肉等對象的建模，不適用于協作機器人柔性關節所表現出的正逆程強非線性、非對稱的復雜遲滯特性建模。

而加權最小二乘支持向量機（WLSSVM）通過引入加權規則改善LSSVM的抗干擾性能和建模精度欠佳的問題[14]，使之能更好地適用于柔性關節的復雜遲滯建模。并且帶中間變量的非線性自回歸移動平均滑動（NARMAX）模型結構是針對非線性系統的一種輸入輸出描述，能有效地表征其動態特性，具有較強的預測復雜非線性輸出的能力。因此，本文為構建協作機器人柔性關節高精度遲滯模型，結合實際關節實驗數據，基于NARMAX結構框架，將PI算子產生的中間變量、輸出力矩歷史值和扭轉角歷史值作為模型輸入，利用LSSVM模型輸出誤差信息，在目標優化函數中采用具有自適應調整因子的輸出誤差信息構成的正則化項，建立改進的WLSSVM遲滯模型。

1 基于 NARMAX 結構的改進 WLSSVM 遲滯模型

1.1 LSSVM 遲滯模型的構建

LSSVM將原本數據空間借助核函數定義的非線性映射，轉換到高維特征空間中，使非線性回歸問題變成高維特征空間下線性回歸問題的求解[11]。在高維空間中構建關節的回歸函數如下。

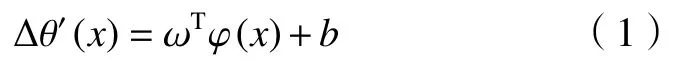
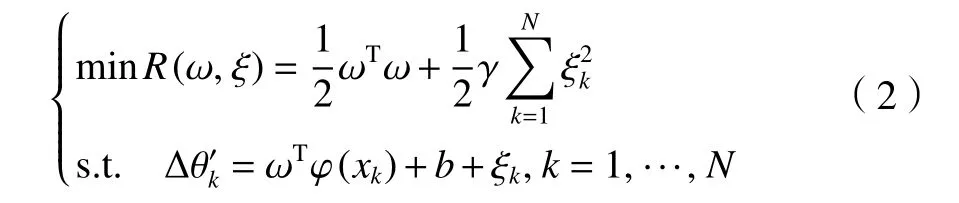
式中： γ為正則化因子； ξk為模型輸出與實際輸出之間的誤差。為求解式（2）的優化問題，構造拉格朗日方程如下

式中： λk表示拉格朗日乘子。為求目標函數的最小值，令式（3）中的變量ω 、b、 ξk及λk偏導數等于0，即

消去式（4）中的 ω 和 ξ，則所求的優化問題轉化為如下線性方程組

式 中 ： λ =[λ1,λ2,···,λN]T， Δ θ′=[Δθ1,Δθ2,···,ΔθN]T，E=[1,1,···,1]T，I代表單位矩陣。因此，LSSVM的優化問題由式（2）轉化為式（5）線性方程組的求解，該方程組用最小二乘法計算。

為避免上述映射函數與高維特征內積φ(x)Tφ(xk)的求解，根據Mercer條件，存在映射函數 φ和核函數K，使得

式中：選取高斯徑向核函數， σ為核函數寬度，‖·‖代表歐氏距離。因此，得到協作機器人柔性關節的LSSVM遲滯模型表達式為

LSSVM遲滯模型的輸入向量選取如下，為

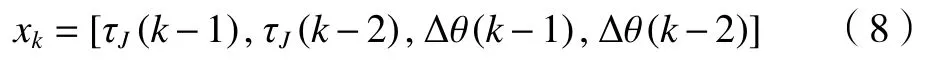
式中：τJ(k-1)和τJ(k-2)表示k-1和k-2時刻實際測得關節力矩， Δ θ(k-1)和 Δ θ(k-2)表示k-1和k-2時刻實際測得關節扭轉角。選取合適核函數參數及正則化參數后，利用LSSVM得到模型的預測輸出扭轉角 Δ θ′(k)，如圖1所示為LSSVM遲滯模型結構圖。

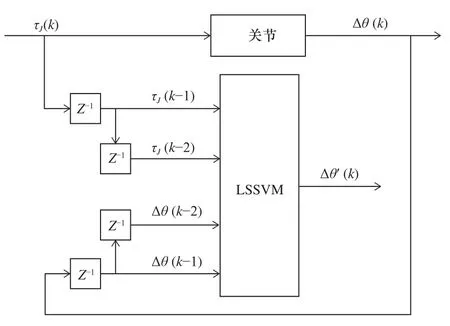
圖1 LSSVM 遲滯模型結構圖

通過協作機器人關節實驗所采集的數據對LSSVM遲滯模型進行驗證。如圖2所示為模型預測輸出與誤差，其中，圖2a實線表示關節實際扭轉角輸出，點畫線表示LSSVM遲滯模型預測輸出，圖2b虛線表示預測誤差。結果表明，LSSVM遲滯模型在預測復雜非線性特性的能力不足，具體表現為關節往返切換運動過程中的預測誤差較大。

1.2 改進 WLSSVM 遲滯模型的構建

1.2.1 基于 PI遲滯算子的中間變量

由圖2可知，針對協作機器人關節的強非線性、非對稱的復雜遲滯特性，LSSVM遲滯模型的預測能力不足。為此，基于NARMAX模型結構特點，在引入輸出力矩和扭轉角歷史值的基礎上，采用PI遲滯算子產生中間變量，將關節遲滯特性的多值映射關系轉化為一對一映射。PI遲滯算子的數學表達式

圖2 LSSVM 遲滯模型預測輸出與誤差

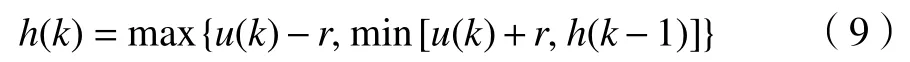
式中：u(k)表示算子輸入，h(k)為算子輸出，閾值r取值為10。當k=0時PI遲滯算子初始化為

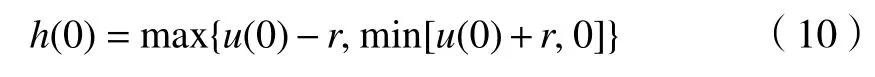
1.2.2 自適應調整因子kξ的設計

為了提高模型的精度和抗干擾能力，根據LSSVM模型輸出與目標值的訓練誤差構成目標優化函數的正則項。本文設計自適應調整因子kξ，正則項不同的權重，決定數據點對建模過程的影響大小，其優化目標函數為

式（11）中所提出kξ表達式如下。

為了求解式（11）的優化問題，構造拉格朗日方程

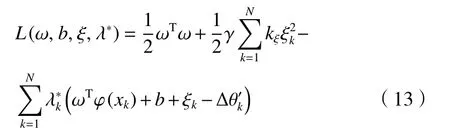
為求目標函數的最小值，令式（13）中變量 ω、b、 ξk及 λ*k偏導數等于0。則所求優化問題轉化為線性方程組。

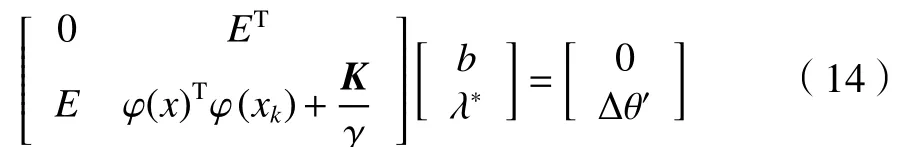
1.2.3 模型參數的優化

在建模過程中，需要預先給定正則化因子 γ和核函數寬度 σ。參數選取能有效提升遲滯模型的預測和泛化能力。而SSA作為一種新的智能優化算法，在收斂速度、搜索精度和局部最優值的避免上具有較高的優勢[15]，故將SSA用于改進WLSSVM遲滯模型的參數選取。

SSA是受麻雀群體捕食行為啟發而提出的優化算法，其運算過程由發現者、追隨者及預警者組成。具有良好適應度值的發現者負責引導麻雀群覓食，其位置更新公式為

式中：j=1,2,···,d為當前維度；t為當前迭代次數；tmax為最大迭代次數；表示t+ 1次迭代下第i只麻雀在第j維的位置； α ∈(0,1]表示隨機數；Q表示服從正態分布的隨機數；L為 1 ×d且元素均為1的矩陣；R2∈[0,1]為預警值；ST∈[0.5,1]為安全值。

追隨者比發現者的適應度值低，需根據發現者的位置來進行捕食，其位置更新公式為

式中：XPt+1表示第t+ 1次迭代時發現者的最優位置；Xwtorst為當前全局最差位置；A+=AT(AAT)-1且A是元素隨機為1或 - 1的 1 ×d維矩陣，n為麻雀總數。

當意識到危險時，預警者會做出反捕食行為，其位置更新公式為

SSA同時優化模型參數 γ和 σ步驟如下：

（1）參數設置及種群初始化，具體為初始參數 γ和 σ，麻雀總數n，最大迭代次數tmax，預警值R2，發現者和預警者數量。

（2）以訓練和驗證均方誤差為適應度函數，計算每只麻雀適應度值fi并排序，得出全局最優和最差適應度值fg和fw。

（3）利用式（16）~（18）更新發現者、追隨者及預警者新位置及對應適應度值，如果適應度值優于前次，則更新。

（4）重復步驟（3）的更新過程直到最大迭代次數，最優解為所有迭代中適應度值最低的那只麻雀，輸出對應最優參數 γ和 σ。

通過上述步驟優化后獲得模型參數取值為γ=2.73， σ =5。

綜上，改進WLSSVM遲滯模型的輸入向量選取如下

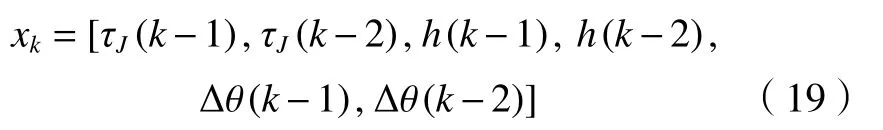
式中：τJ(k-1)和τJ(k-2)表示k-1和k-2時刻實際測得輸出力矩； Δ θ(k-1)和 Δ θ(k-2)表示k-1和k-2時刻實際測得關節扭轉角；h(k-1)和h(k-2)表示k-1和k-2時刻PI遲滯算子的輸出。利用SSA獲取最優核函數參數及正則化參數后，通過改進WLSSVM，得到預測輸出扭轉角 Δ θ′(k)，如圖3所示為改進WLSSVM遲滯模型結構圖。

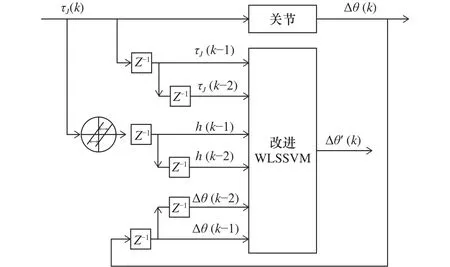
圖3 改進 WLSSVM 遲滯模型結構圖

2 遲滯模型的建模與驗證實驗

本文搭建協作機器人柔性關節遲滯特性實驗平臺，通過實驗得到輸出力矩與扭轉角的關節數據。以最大絕對誤差（MAE）和均方根誤差（RMSE）作為模型精度的評判指標，分別比較LSSVM遲滯模型、在 IEEE-ASME T MECH期刊中文獻[16]所提NARMAX遲滯模型和改進WLSSVM遲滯模型的建模與驗證效果。

2.1 關節數據的采集

實驗平臺由FRANKA協作機器人、控制器和工作站PC組成。工作站PC需為配置實時內核的Ubuntu環境，并裝有Libfranka庫。在Visual Studio Code中利用C++編程訪問FCI，使FRANKA協作機器人指定關節按給定位置信號做雙邊正弦衰減運動，同步采集扭轉角與輸出力矩的數據。

實驗過程如下，給定關節位置信號qd為

式中：A為 關節運動幅度，（°）；T為關節一個回環運動的時間，s；時間常數τ取為0.02，關節運動回環設為6個，采樣頻率設為10 ms。

為充分驗證所提模型的性能，采集不同幅度和周期下的關節實時數據，取值分別為：①A=π/6,T=4s； ②A=π/6,T= 6s； ③A=π/8,T= 4s ；④A=π/7,T= 5s。將所采集數據分別用于改進WLSSVM遲滯模型和對比遲滯模型的建模與驗證。

2.2 建模與驗證結果

將A=π/6,T= 4s時的關節數據作為模型訓練數據。如圖4所示為建模輸出遲滯圖，如圖5所示為建模輸出和誤差時域圖。分析圖5可知，LSSVM遲滯模型、NARMAX遲滯模型和改進WLSSVM遲滯模型的建模MAE分別為 0.004 53°、0.003 48°和0.001 87°， 對 應 的 建 模RMSE分 別 為 0.001 81、0.001 20和0.000 45。所提模型比LSSVM遲滯模型的建模MAE降低2.4倍，建模RMSE降低4.0倍，比NARMAX遲滯模型的建模MAE降低1.9倍，建模RMSE降低2.7倍。

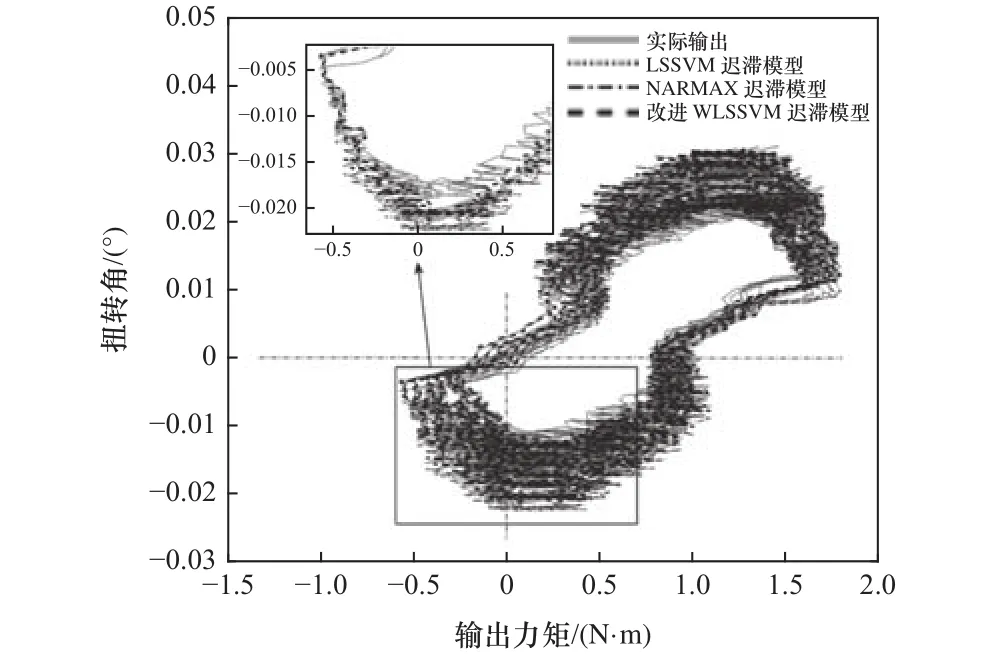
圖4 建模輸出遲滯圖

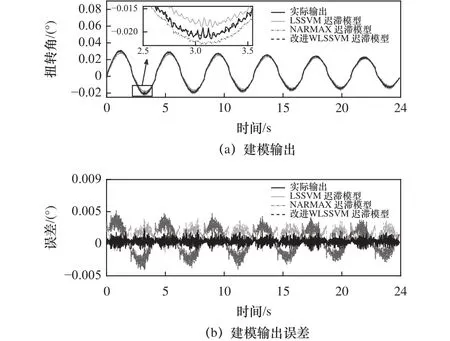
圖5 建模輸出和誤差時域圖

將A=π/6,T= 6s時的關節數據用作模型第一組驗證數據，其驗證輸出遲滯關系如圖6所示，時域下的驗證輸出和誤差如圖7所示。分析圖7可知，LSSVM遲滯模型、NARMAX遲滯模型和改進WLSSVM遲滯模型驗證MAE分別為 0.003 24°、0.003 13°和0.001 39°，對應驗證RMSE分別為0.001 06、0.001 11 和0.000 41。所提模型比LSSVM遲滯模型和NARMAX遲滯模型的驗證MAE均降低2.3倍，而驗證RMSE分別降低2.6倍和2.7倍。

圖6 第一組驗證數據輸出遲滯圖

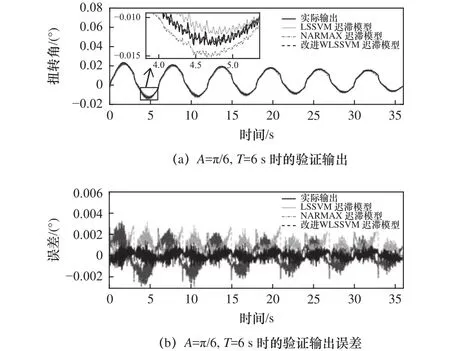
圖7 第一組驗證數據輸出和誤差時域圖

將A=π/8,T= 4s時的關節數據用作模型第二組驗證數據，如圖8所示為驗證輸出遲滯圖，如圖9所示為驗證輸出和誤差時域圖。分析圖9可得，LSSVM遲滯模型、NARMAX遲滯模型和改進WLSSVM遲滯模型驗證MAE分別為 0.003 32°、0.003 12°和0.001 65°，對應驗證RMSE分別為0.001 32、0.001 14和0.000 41。所提模型比LSSVM 遲滯模型和NARMAX遲滯模型的驗證MAE分別降低2.0倍和1.9倍，而驗證RMSE分別降低3.2倍和2.8倍。

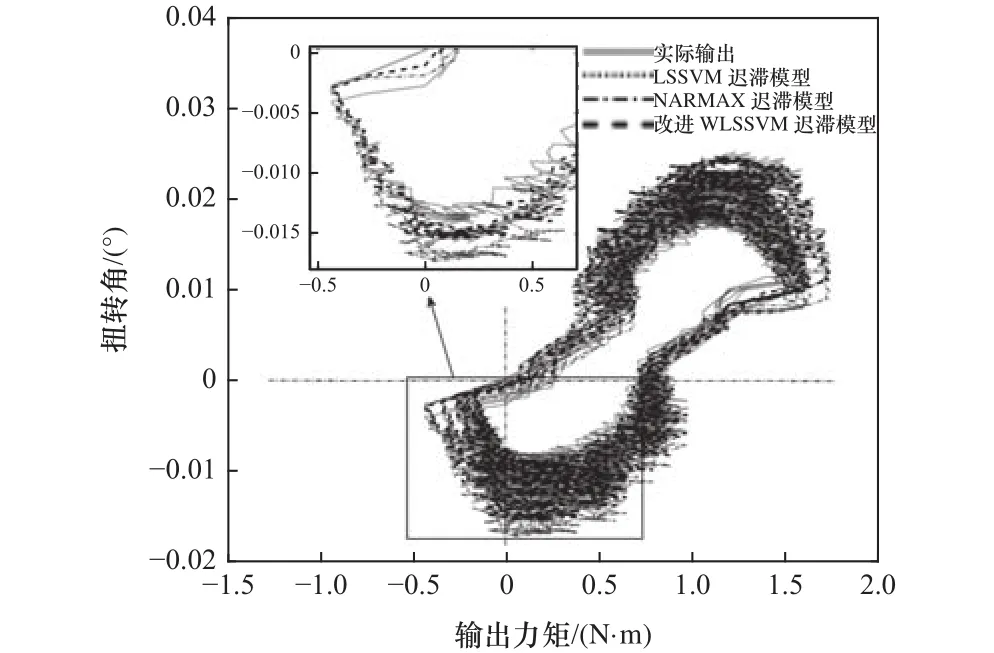
圖8 第二組驗證數據輸出遲滯圖

將A=π/7,T= 5s時的關節數據用作模型第三組驗證數據，得到驗證輸出遲滯曲線如圖10所示，時域下驗證輸出和誤差對比如圖11所示。分析圖11可得，LSSVM遲滯模型、NARMAX遲滯模型和改進WLSSVM遲滯模型的驗證MAE分別為0.003 31°、0.003 22°和0.001 74°，對應驗證RMSE分別為0.001 14、0.001 10和0.000 40。所提模型比LSSVM 遲滯模型和NARMAX遲滯模型的驗證MAE均降低1.9倍，而驗證RMSE分別降低2.9倍和2.8倍。

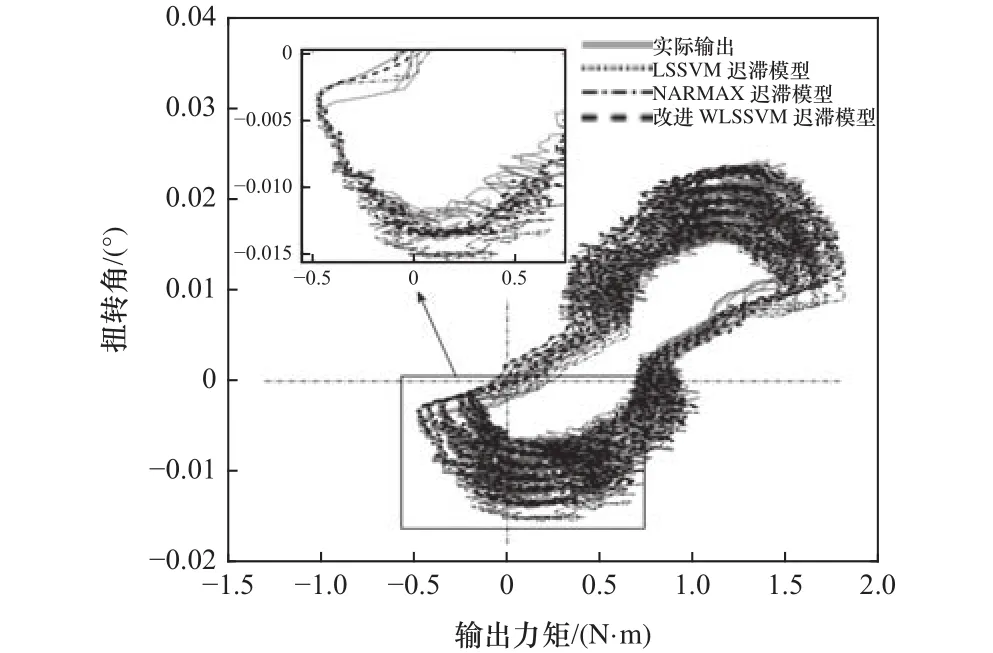
圖10 第三組驗證數據輸出遲滯圖

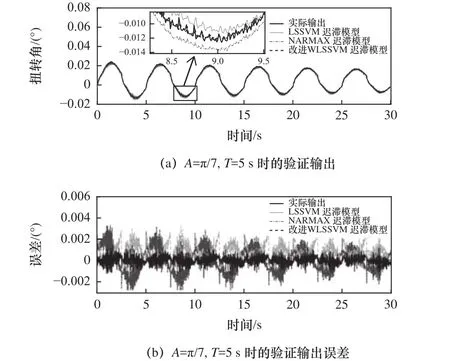
圖11 第三組驗證數據輸出和誤差時域圖

不同周期和幅度下的模型驗證結果對比如表1所示。可知，相較于LSSVM遲滯模型，所提模型的驗證MAE最多降低2.3倍，驗證RMSE最多降低3.2倍。相較于NARMAX遲滯模型，所提模型的驗證MAE最多降低2.3倍，驗證RMSE最多降低2.8倍。綜上，改進WLSSVM遲滯模型的模型精度和泛化能力均優于LSSVM遲滯模型和NARMAX遲滯模型。

表1 不同周期和幅度下的模型驗證結果對比

3 結語

針對由諧波減速器構成協作機器人柔性關節所表現出的多值對應、強非線性和非對稱性的復雜遲滯特性問題，提出基于NARMAX結構的改進WLSSVM遲滯模型。利用PI算子所產生的中間變量、輸出力矩歷史值和扭轉角歷史值作為模型輸入，解決多值映射問題。在優化目標函數的正則化項中引入自適應調整因子，使模型可以有效預測非對稱和強非線性特性。結果表明，相較對比模型，所提遲滯模型具有較優的驗證精度。