微細電解加工恒精度變參數采樣算法＊

趙傳軍 黃天用 王冀鵬 許立忠

（燕山大學機械工程學院，河北 秦皇島 066004）

精密加工是現代高科技產業和科學技術發展的基礎，也是現代制造科學的重要發展方向[1]，其加工尺寸、形狀精度能夠達到亞微米級[2-3]。微細電解加工技術（electrochemical micromachining，ECMM）作為實現精密加工的主要方法之一，其加工過程中工件以離子形式溶解蝕除、無切削應力、不受材料硬度的限制。因此，使用ECMM加工零件的機械性能遠高于傳統機械加工方法[4]。但是，ECMM仍需要借助傳統機械加工的數控系統及插補算法程序作為載體。在微機電系統、軍事醫療等高精尖科技領域，常遇到精密微型復雜曲線及曲面的加工。對于這些以參數方程形式表達的復雜曲面與輪廓，通常采用數據采樣法 (data sampling method, SDM)進行加工[5-6]。即采用連續直線或圓弧軌跡對加工曲線輪廓進行擬合，然后對每一段擬合軌跡進行插補完成復雜輪廓的加工[7-9]。

對于ECMM，雖然通過傳統的弦長或弧長逼近算法能夠加工出近似形狀的曲線，但這種處理方法會產生較大的弓高誤差[10-11]，造成切線速度不連續[12]。與傳統切削加工方法相比，ECMM工況更為復雜。在電解加工過程中，微電極并不是沿加工軌跡始終做前進運動，而是要根據當前的加工狀態（短路與否），來判定下一步運動要前進還是回退。短路回退機制決定了ECMM無法遵照SDM規劃好的軌跡和速度來運動，而且加工兩點拐角處的速度損失，會延長陽極加工時間，增大材料蝕除量，降低加工精度。因此，采用SDM難以滿足ECMM亞微米級精度要求[13-14]。

為了解決這一問題，韓國Yang M Y等[15]通過縮短SDM采樣間隔，開展了NURBS曲線線切割加工實驗，最小加工誤差達到0.91P(P為脈沖當量)。縮短采樣間隔會大幅增加程序代碼數量，增大系統運算負荷，降低加工效率。上海交通大學陳昊[16]等研究了電火花線切割中基于單位弧長增量法的參數曲線插補方法，簡化程序代碼的同時避免了速度損失，其加工誤差能夠控制在3P以內。該算法核心是引用弧長公式將角度參數方程轉化為弧長參數方程，但會造成二次誤差累計，降低加工精度，不適用于微細尺度零件的精密加工。基于逐點比較法的等參數離散法[17]，當加工曲線曲率變化較大時，兩相鄰離散點之間的距離隨著曲率變化會產生較大的偏差和弓高誤差，適用于形狀精度要求不高的場合。

為了滿足ECMM特殊工況和精密加工要求，本文基于參數離散法思想[18]，提出一種能夠實現恒精度控制的變參數在線采樣算法。本算法根據精度要求自動優化調整步長，實時控制加工曲線形狀精度和軸向偏差。算法編程簡便，無需預先存儲大量代碼，通過軸向偏差在線計算、分析，實時調整采樣參數增量，控制刀具運動軌跡。該算法尤其適用于需要實時檢測加工狀態的微細特種加工技術。

1 恒精度變參數采樣法

1.1 算法原理

由于機床加工分辨率δ無法超過機床脈沖當量P，可以近似認為機床所能達到的最高極限加工精度為其脈沖當量P。實際上，零件加工受眾多誤差因素影響，難以達到等同于機床脈沖當量的極限加工精度。但是，通過對機床各軸脈沖當量運動的合理精準控制，能夠將機床加工精度最大化。

對于初始參數為t0的任意參數曲線方程曲線初始點坐標為P0[f(t0),g(t0)]，對參數t取增量 Δt得曲線離散采樣點P1[f(t0+Δt),g(t0+Δt)]。則曲線在x軸和y軸方向的增量分別為Δx1=f(t0+Δt)-f(t0)和Δy1=g(t0+Δt)-g(t0+Δt)。每個運動軸占用2個累加寄存器EA1和EA2，分別用來記錄該軸當前增量和預存儲下一增量。

設工件要求加工精度為δ，令δ=kP，k為精度控制系數 (k≥0.5)，將各軸向偏差|Δ| (|Δx|或|Δy|)分別與加工精度進行比較如下：

（1）當某一軸向偏差|Δ|≤kP時，該軸的下一步運動暫停。

（2）當軸向偏差kP＜|Δ|＜2kP時，該軸向逼近曲線方向運行一個步進距S(S=aP，a為脈沖數；機床運動步進距S應為脈沖當量P的整數倍，因此a∈N*。當k≤1時，取a=1；當k＞1時，a向上取整)，運行后刀具與目標點之間軸向偏差|Δ′|＜2kP-S。

（3）當各軸向偏差均小于kP或任意軸向偏差大于2kP時，說明采樣參數增量Δt選取過密或過疏，需要通過二分法重置Δt。

算法運行一步后，需要根據各軸運動步進距S計算當前刀具軌跡點坐標，然后重置參數增量Δt求解曲線下一采樣點，并重新根據采樣點與刀具坐標之前軸向偏差判斷各軸運動狀態。該算法用于具有短路回退機制的特種加工技術時，當發生短路時只需從寄存器中讀取曲線上一采樣點坐標，即可實現刀具原路徑回退控制。

該變參數在線采樣算法實現了“邊運動邊求解”，并不斷通過刀具軌跡坐標實時修正參數采樣增量，控制軸向偏差，保證曲線加工精度。因此，該算法編程十分簡單，無需預先存儲大量代碼，只需輸入曲線參數方程及精度控制系數即可完成復雜曲線的高精度加工，通用性極好。

1.2 算法流程

圖1為變參數在線采樣算法程序框圖，算法具體流程如下。

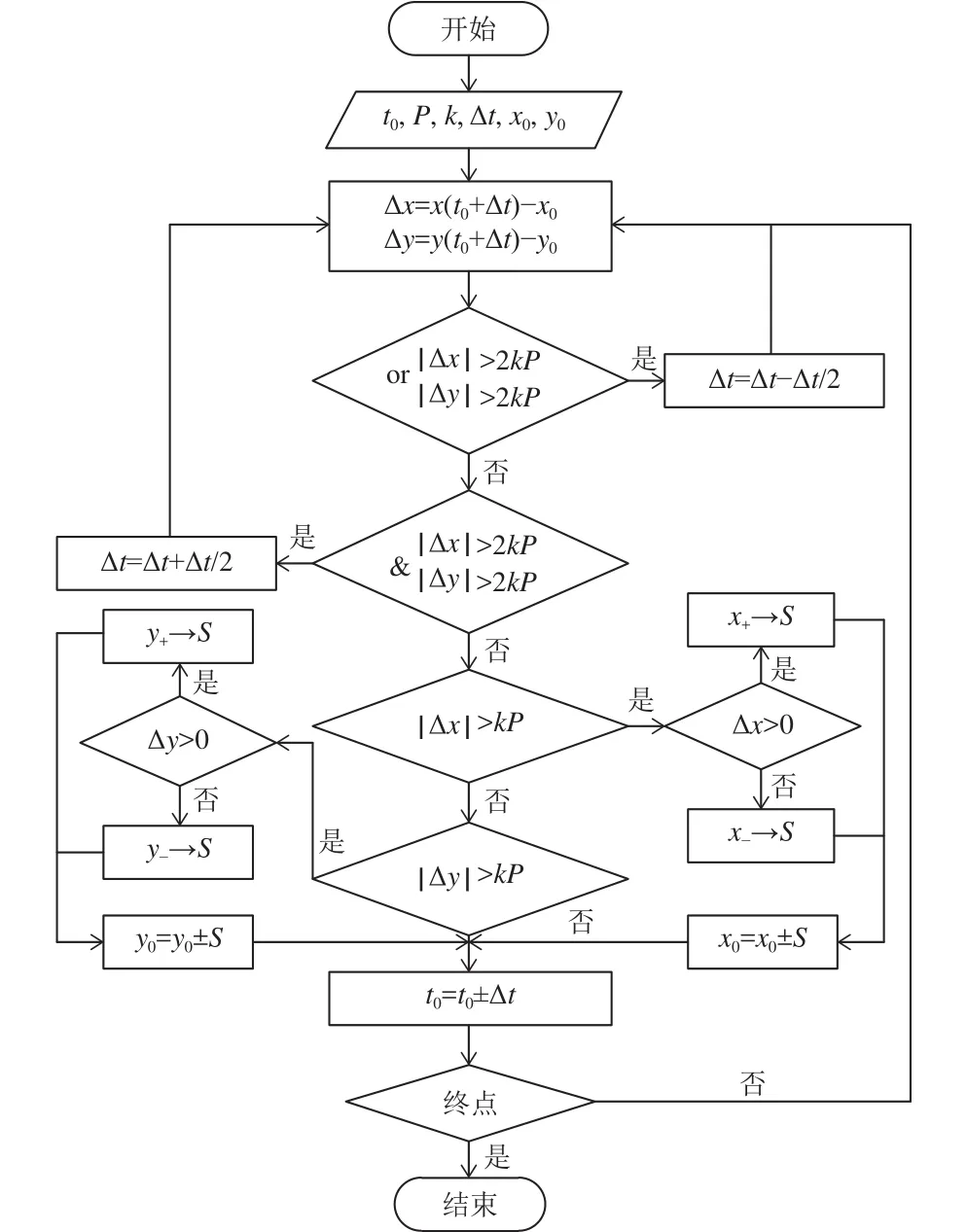
圖1 變參數采樣算法程序框圖

（1）確定初始參數t0、P和k，取Δt=kP。

（2）求解初始點坐標P0[x(t0),y(t0)]和取參數增量后點的坐標P1[x(t0+Δt),y(t0+Δt)]；并計算兩離散點軸向偏差 Δx=x(t0+Δt)-x(t0)和 Δy=y(t0+Δt)-y(t0)。

（3）根據|Δx|和|Δy|的值調整參數增量 Δt并控制各軸相應的運動，坐標軸向偏差|Δ|范圍及對應程序命令如表1所示。

表1 軸向偏差與程序命令執行表

（4）計算刀具運動點的坐標；根據各軸運動執行情況計算刀具當前坐標點Q，以Q點為初始點坐標重復步驟（2）和（3），直至加工完成。

在上述步驟（3）中，參數增量Δt的增大和減小采用二分法快速重置（增大，Δt=Δt+Δt/2；減小，Δt=Δt-Δt/2）。各軸的運動方向需要根據軸向偏差Δ的正負進行判別。以x軸方向為例（y軸方向同理），當Δx＞0時，說明采樣點Pi+1相對于初始點Pi位于x軸的正半軸方向，刀具要向x軸的正方向運動逼近目標采樣點Pi+1；反之，當Δx＜0時，刀具要向x軸的負方向運動逼近目標采樣點Pi+1。

1.3 算法加工仿真

以阿基米德螺旋曲線加工為例，取參數離散法與恒精度變參數采樣法，對二者加工軌跡和軸向偏差進行對比分析。所加工螺旋曲線參數方程為

為了便于加工曲線軌跡點的圖形化表達，取機床脈沖當量P=0.02 mm，工件加工精度δ=0.02 mm，精度控制系數k=δ/P=1。令參數初始值t0=0，參數增量Δt=kP=0.02。利用MATLAB對常用參數離散算法和變參數采樣算法進行仿真對比分析。

圖2是根據參數離散算法繪制的螺旋線加工離散點仿真圖，即將所加工曲線通過參數離散法求出各離散點坐標，然后通過兩相鄰點的直線加工近似代替曲線加工。從圖2a可以看出，雖然各離散點參數增量取值相同 (Δt=0.02)，但是由于所加工螺旋線曲率隨參數t的增大逐漸減小，其軸向偏差也隨之增大，兩相鄰離散點之間的距離（弦長）也會逐漸增加，導致加工曲線弓高誤差隨之增大。

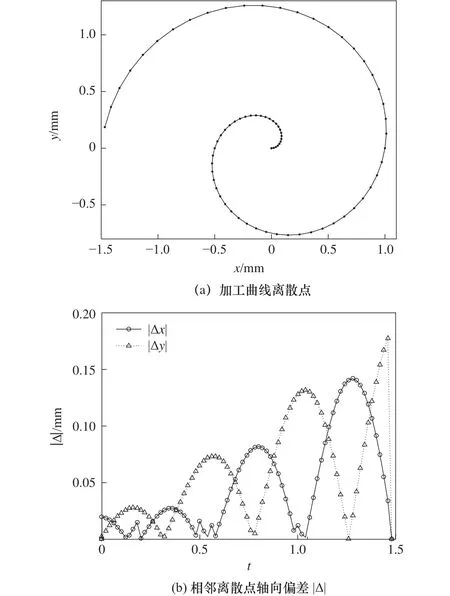
圖2 參數離散算法仿真

圖2b為采用參數離散算法時相鄰離散點軸向偏差圖。在t0初始位置，螺旋線曲率較大，參數離散點較密集，x軸和y軸均會出現軸向偏差小于機床脈沖當量P的情況。這不僅會影響加工效率，而且容易出現加工丟步現象，造成加工曲線局部失真。隨著參數t的增大，x軸和y軸向偏差逐漸增大，其最大值分別為 0.161 9 mm 和 0.177 6 mm，遠大于機床脈沖當量P。因此，當采用弦長逼近法加工該螺旋線時，會產生較大的形狀誤差。

圖3為采用變參數采樣算法加工螺旋線的采樣點仿真圖。從圖3a中可以看出，通過對采樣參數增量的在線調控，加工螺旋線任意兩相鄰軌跡點之間的距離不再隨曲率變化，兩相鄰離散點之間的距離十分均勻。通過兩相鄰軌跡點軸向偏差變化圖（圖3b）可以看出，隨著參數t的增大，相鄰軌跡點之間的軸向偏差|Δx|和|Δy|始終控制在 0.04 mm(2kP)內，其最大值分別為 0.039 9 mm 和 0.037 6 mm。在運行一個步進距S=aP=0.02 mm后，刀具坐標距曲線離散點之間軸向偏差最大值分別為|Δ′x|max=0.019 9 mm 和|Δ′y|max=0.017 6 mm，均小于機床脈沖當量P，且在加工精度δ要求之內。圖3b中軸向偏差|Δx|和|Δy|突變處，是由于兩相鄰離散點之間的軸向偏差|Δ|＞2kP時，對參數增量Δt重置后造成的。

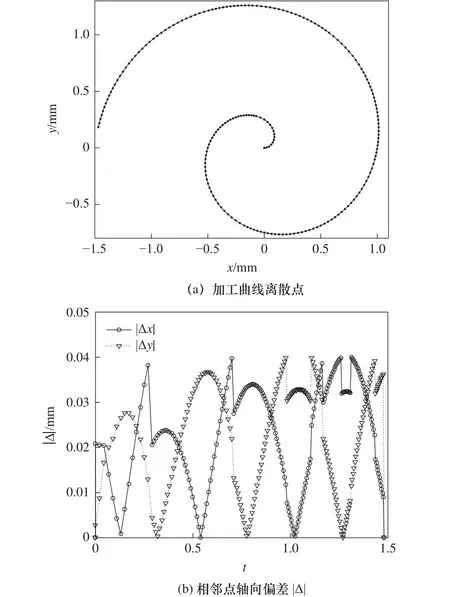
圖3 變參數采樣算法仿真

通過上述對比分析可以看出，變參數采樣法能夠根據加工精度要求控制相鄰采樣點的軸向偏差，自動優化刀具運行軌跡，在滿足加工精度的同時提高加工效率，更適用于精密微細尺寸零件的加工。

2 算法精度分析

2.1 精度控制系數對加工精度的影響

變參數采樣法通過對曲線采樣參數增量的在線實時調控，將復雜曲線兩相鄰離散點之間的軸向偏差控制在(kP, 2kP)內。在機床運行一個步進距S后，二者偏差|Δ′|＜2kP-S，將S=aP,δ=kP代入不等式得

當1/2＜k≤1時，a=1，代入不等式（2）得|Δ′|＜δ；當k＞1 時，a向上取整，則k≤a＜k+1，代入不等式（2）得|Δ′|≤δ。因此，無論k和P取何值，加工曲線與刀具之間軸向偏差始終控制在加工精度之內，實現復雜曲線加工的恒精度控制。利用不等式（2），圖4給出了曲線與刀具之間軸向偏差|Δ′|隨精度控制系數k的變化規律。

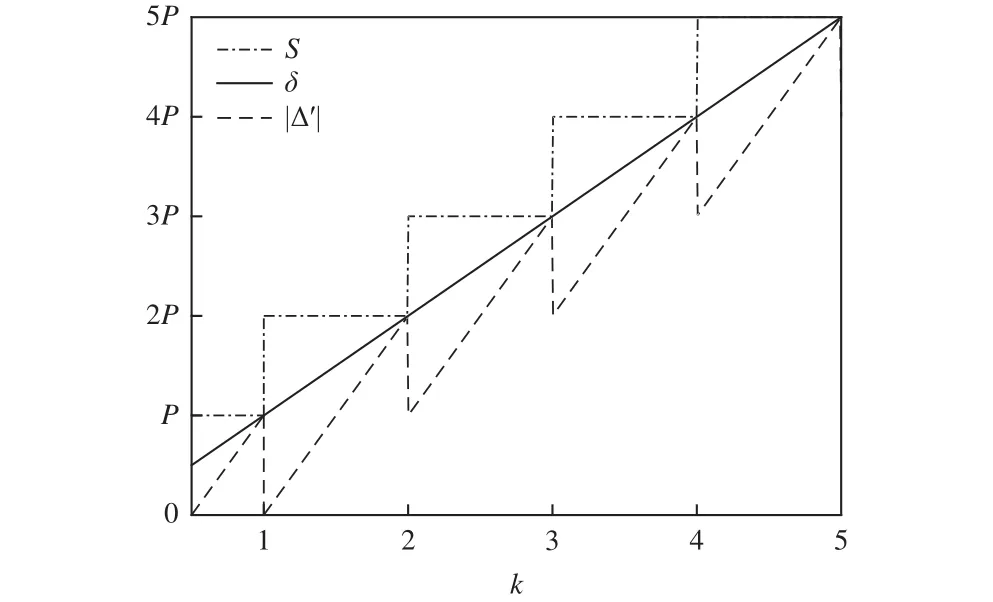
圖4 軸向偏差|Δ′|隨 k 的變化

從圖4可以看出，隨著精度控制系數k的增大，加工精度δ和偏差|Δ′|逐漸增大，步進距S成倍增加。在同一整數段內，k的取值越大，曲線與刀具之間軸向偏差|Δ′|越大，且始終小于要求精度δ。

例如：當k=0.8時，a=1，|Δ′|＜2kP-aP=0.6P＜kP；當k=2.2 時，a=3，|Δ′|＜2kP-aP=1.4P＜kP；當k=2.8時，a=3，|Δ′|＜2kP-aP=2.6P＜kP。因此，在給定加工精度要求后，能夠確定k的取值分段，在該分段內k越小，軸向偏差|Δ′|越小，加工精度越高。

為了進一步分析精度控制系數k對曲線加工精度的影響，分別取k=0.8和2，利用變參數采樣法對螺旋曲線加工進行仿真分析，如圖5所示。圖5b和5d中，|Δ′|為機床運行一個步進距S后，刀具中心點與曲線采樣點之間的軸向偏差。對比圖5a和5c可以看出，在進行同一尺度參數曲線加工時，精度控制系數k取值越小，曲線軌跡點越密集，弓高誤差越小，加工精度越高。當k=0.8時，刀具中心點與曲線離散點之間軸向偏差最大值|Δ′|max=0.011 9＜0.8P；當k=2 時，|Δ′|max=0.039 7＜2P。

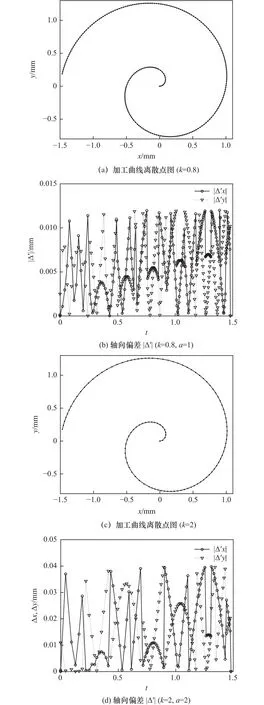
圖5 變參數采樣算法偏差|Δ′|仿真

通過上述分析可知，當加工曲線要求精度較高時，取精度控制系數k≤1 (k=δ/P)，能夠將曲線軸向偏差控制在脈沖當量以內，提高加工精度。當加工曲線所要求精度不高時，取精度控制系數k＞1，可以減少參數離散點的數量，增大機床步進距，提高加工效率。因此，通過對精度控制系數k的選取，本算法不僅能夠實現精密微細加工，也可以完成普通精度的高效加工，適用性廣。

2.2 算法形狀誤差

圖6是基于變參數采樣算法的曲線加工軌跡示意圖，圖中點Pi為曲線上的采樣點，點Qi為刀具運動軌跡點。圖中可以看出參數曲線的形狀誤差實際上就是刀具軌跡點偏離原加工曲線的最大距離[19-20]。其形狀誤差ε可以用刀具中心坐標點Qi到兩離散點Pi-1和Pi連線之間的垂直距離來衡量。令這三點的坐標分別為Q(ui,vi)，Pi-1(xi-1,yi-1) 和Pi(xi,yi)，則加工曲線形狀誤差ε為

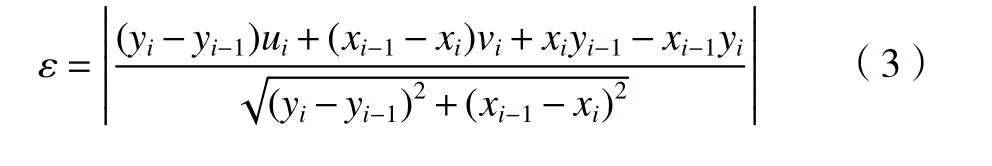
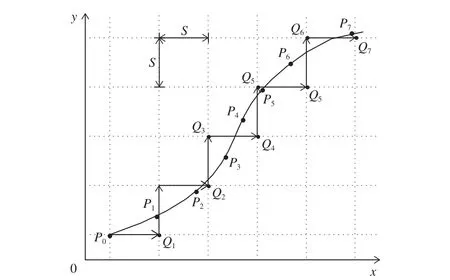
圖6 曲線加工軌跡示意圖

為了便于同加工實驗結果對比分析，取脈沖當量為微細電解加工實驗機床實際脈沖當量P=0.5 μm，要求加工精度δ＜0.5 μm，精度控制系數k=δ/P=1。取螺旋線螺距30 μm，利用變參數采樣算法進行螺旋曲線加工仿真分析，如圖7所示。圖7a中Pi為螺旋曲線上的采樣點，Qi為刀具軌跡點，在整個螺旋線加工過程中，刀具中心軌跡和加工曲線保持高度一致性。

圖7 算法加工形狀誤差

用點Qi偏離曲線的垂直距離描述其加工形狀誤差，由式2得到加工形狀誤差ε隨參數t變化的散點圖（圖7b）。從圖中可以看出，在整個曲線加工過程中，刀具中心點偏離加工曲線的最大距離εmax=0.346 μm≈0.69P（若取精度控制系數k＜1，曲線形狀誤差會隨之減小）。即利用本算法進行曲線加工所產生的最大形狀誤差只有機床脈沖當量的0.69倍，低于參數離散法的0.91P與單位弧長法的3P。該變參數采樣法通過對曲線參數增量Δt及軸向步進距S的在線實時調控，進一步提高了機床的微細加工能力，為該算法在精密微細加工中的應用提供理論基礎。

3 算法加工實驗

為了驗證精度自適應控制算法在微細加工領域的可行性，在電解加工實驗平臺上進行了螺旋線和圓形參數曲線微細加工實驗，實驗機床脈沖當量P=0.5 μm。基于變參數采樣法開發了參數曲線加工控制程序，如圖8所示。陰極電極用直徑0.1 mm的鎢絲通過電化學腐蝕加工制成，其末端直徑為10 μm（圖9）。陽極工件為厚度5 μm的X12CrNi177鎳基不銹鋼薄片，電解液取濃度0.1 mol/L的H2SO4溶液。在前期工藝參數優化研究的基礎上[21]，利用脈沖微細電解加工方法進行參數曲線微細電解加工實驗，實驗結果如圖10所示。

圖8 參數曲線加工控制程序

圖9 微細電解加工電極

圖10 基于變參數采樣算法的微結構加工

圖10a是通過阿基米德螺旋線加工得到的微曲梁結構，取算法精度控制系數k=0.8，則所能達到加工精度δ≤kP=0.4 μm。從圖中可以看出，通過精度自適應控制算法加工得到的螺旋微槽邊緣清晰、形狀規整，槽寬 10.56 μm，加工側隙約 0.25 μm。圖10b為通過弧形加工得到的圓形微振子結構，取算法精度控制系數k=1，則加工精度δ≤kP=0.5 μm。得加工圓槽寬 10.93 μm，加工側隙約 0.43 μm。取算法精度控制系數k=2 (δ≤kP=1 μm)，同樣進行阿基米德螺旋線加工，加工結果如圖10c所示，曲線槽寬 11.72 μm，加工側隙約 0.86 μm。

上述螺旋線和圓形參數曲線的微細電解加工均達到亞微米級加工精度，且在算法控制精度δ以內。實驗結果表明，該變參數采樣法加工精度隨精度控制系數k取值的增大而降低，通過減小系數k的取值，該算法能夠滿足精密微細加工技術的高精度要求。

4 結語

該恒精度變參數采樣插補算法通過對采樣參數增量及軸向步進距的在線實時調控，將加工刀具軌跡與曲線輪廓之間的軸向偏差始終控制在要求加工精度δ以內。引入精度控制系數k實現復雜參數曲線恒精度加工，k越小加工精度越高。最后，利用該算法進行螺旋線和圓形參數曲線微細電解加工實驗，獲得了亞微米級加工精度，實驗結果同理論分析數據吻合。

該變參數采樣插補算法有以下優點：

（1）算法編程簡單，通用性好，適用于任意復雜參數曲線加工。

（2）加工精度高，能夠獲得優于機床脈沖當量的加工精度；通過改變精度控制系數k，能夠完成精密加工和高效加工兩種模式之間的無縫切換。

（3）算法實現了“邊運動邊求解”，無需存儲大量程序代碼，通過刀具軌跡坐標實時修正參數采樣增量，自動優化調控刀具路徑。