基于改進閾值估計和改進閾值函數的局部放電信號降噪方法
劉志堅,趙浩益,劉 航,羅靈琳,宋 琪,李鵬程
(昆明理工大學 電力工程學院,昆明 650500)
超聲波檢測是一種經典的高壓電力設備局部放電故障源定位和類型識別的基礎方法,對于維護電力系統運行穩定性和安全性有重要意義[1-2]。然而運行經驗表明,現場工作環境中存在大量以白噪聲、電磁噪聲為代表的干擾源,造成局放信號的污染甚至淹沒。因此,如何準確、完整地提取原始超聲波信號,最大程度地抑制干擾成為局部放電監測的關鍵內容[3-5]。
小波變換方法具有多頻段分離、多分辨率分解的能力,在非平穩信號降噪處理中體現出較好的優勢而得到廣泛應用[6-7]。基于小波閾值的降噪方法基本步驟包括:①對原始信號進行小波分解;②對分解后的各系數組分進行降噪處理;③將處理后的各低噪系數組分重構,獲得降噪后的原始信號[8]。在步驟②中,閾值優化估計及閾值函數的選擇和設計是影響降噪效果的重要因素,現有的研究大多圍繞上述兩個關鍵內容來展開。
在閾值優化估計方面:文獻[9-11]構造了含閾值梯度的適應度函數,并基于啟發式算法搜索最優閾值,克服了降噪適應度函數對于標準信號的先驗依賴,為實現閾值梯度構造,此方法要求閾值函數在閾值鄰域內具有連續可導性,所以對于不連續、不可導的閾值函數不具備適應性;文獻[12-15]將時間序列樣本熵理論引入閾值估計中,以估計噪聲序列復雜度為依據,選取噪聲序列最大樣本熵值下的閾值作為最優閾值估計值。然而,這種閾值估計方法存在兩方面局限性:①最大樣本熵指標不能完整描述原始信號中全部噪聲的集合,最大樣本熵下估計的閾值存在偏小風險,使信號降噪不完全;②不同閾值步長下樣本熵極值的搜索精度和搜索速度存在矛盾性,估計的閾值容易陷入局部解。針對局限性①,目前鮮有相關研究和解決辦法;針對局限性②,有研究考慮采用啟發式算法優化最大樣本熵,避免人為選擇步長對尋優誤差的影響,但其基本原理仍然是基于最大樣本熵的閾值估計,并沒有克服局限性①帶來的問題。
在閾值函數改進方面:文獻[16]構建了一種在閾值處連續且可導的閾值函數,以改進傳統閾值函數存在的重構偏差和過度降噪缺陷;文獻[17-19]提出介于軟、硬閾值之間的連續閾值函數。上述提出的各種閾值函數改進形式不同,但均可以通過調整函數攜帶的參數在不同程度上實現對軟、硬閾值函數缺陷的改善,達到提升降噪效果的目的,但是存在著參數選擇討論不充分、函數臨界閾值處不可導、系數處理過渡不平滑的情況,在一定程度上影響了重構信號的質量。
在上述研究的基礎上,提出一種基于快速綜合熵和改進閾值函數的局部放電信號小波降噪方法。首先,建立了融合噪聲序列樣本熵和降噪序列樣本熵的綜合熵模型,使用二分變步長迭代方法實現了最優閾值的快速估計;進而,提出一種融合軟、硬閾值特征的新型閾值函數,該函數的連續平滑過渡特征能夠有效抑制原始信號的重構振蕩和重構偏差;最后,使用多個高壓電力設備局部放電超聲波脈沖信號開展仿真和測試,對本文所提降噪方法的有效性進行了驗證。
1 局部放電超聲波模型及小波降噪基本流程
1.1 局部放電超聲波信號數學模型
電力設備長期運行在高壓電磁環境下,隨著工作時間的增加,當設備絕緣出現局部缺陷時,會在該區域產生伴隨聲、光放射的放電現象,稱為局部放電(partial discharge,PD),簡稱局放。局放源屬于點源,其產生的超聲波信號以簡諧波的形式向周圍環境輻射,常見的局放超聲波信號數學模型如式(1)所示[20]
(1)
式中:A0為幅值;t0為初始時間;τ為衰減常數;f為衰減振蕩頻率。
根據式(1)模型,標準的局放超聲波時域仿真信號如圖1(a)所示,可見局放超聲波是一種高頻振蕩的衰減信號,運行環境中產生的局放超聲波信號往往會受到各種噪聲干擾,含噪的超聲波脈沖時域仿真信號如圖1(b)所示。實際上,在帶絕緣缺陷的電力設備運行中,并不是僅僅產生一次局放現象,而是在同一局放源處會以一定的時間間隔周期性地發生局部放電,時域仿真信號如圖1(c)所示。
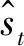
(2)
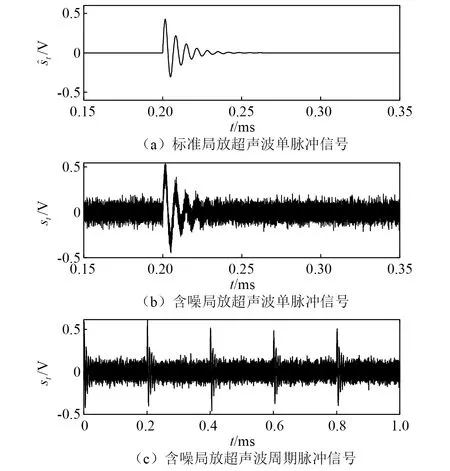
圖1 局部放電超聲波信號模型Fig.1 Model of partial discharge ultrasonic signal
1.2 基于小波理論的局放超聲波信號降噪過程
基于小波閾值的信號降噪基本過程如下:
步驟1小波分解——選擇合適的小波基與分解層數對原始信號進行尺度分解,得到各頻段的小波系數;
步驟2系數處理——確定系數處理的閾值,通過閾值函數對高頻小波系數去噪處理得到降噪系數;
步驟3信號重構——基于步驟2得到的降噪系數與低頻系數完成信號重組,實現信號降噪。
其中,步驟2的閾值選取和閾值函數設計反映了系數處理的映射規則,會對降噪質量產生重要影響,是小波閾值去噪的重要環節,本文從最優閾值估計和閾值函數改進兩個方面實現對傳統閾值函數降噪方法的優化。
2 基于綜合熵的最優閾值估計方法
2.1 基于樣本熵的閾值估計基本原理及不足
2.1.1 樣本熵基本理論及閾值估計應用
(1) 樣本熵基本理論
樣本熵通過計算一維時間序列中新模式的生成概率來反映序列混亂度,由于具有良好的噪聲序列復雜度表征能力而被廣泛引入到閾值估計中,針對長度為N的信號序列Xi={x1,x2,…,xN},其樣本熵值計算過程如下:
步驟1設定嵌入維數m和相似容限r,考慮維數為m的向量組{xm(1),…,xm(N-m-1)},其中
Xm(i)={x(i),x(i+1),…,x(i+m-1)}
(3)
步驟2設兩個向量Xm(i)和Xm(j)之間的距離d[Xm(i),Xm(j)]為向量之間對應元素之差絕對值的最大值,其表達式為
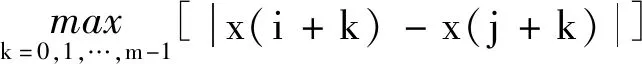
(4)
步驟3設定固定的Xm(i),對Xm(i)和Xm(j)之間的距離小于等于相似容限r的數目j(1≤i≤N-m,j≠i)進行統計,并記作Bi,定義兩個向量在相似容限下匹配m個點的概率,記作Bm(r),其表達式為
(5)
(6)
步驟4將嵌入維數增加到m+1,按照上述計算Xm+1(i)與Xm+1(j)之間的距離小于等于相似容限r的數目j(1≤i≤N-m,j≠i)進行統計,記為Ai,定義兩個向量在相似容限下匹配m+1個點的概率,記作Am(r),其表達式為
(7)
(8)
步驟5定義序列樣本熵(sample entropy,SE)為
(9)
實際信號中N通常為有限值,樣本熵估計為
(10)
根據上述步驟,樣本熵的計算與參數m,r取值有關,在實際應用中,一般取m=1或m=2,r=0.1std(X)~0.25std(X),std(X)為時間序列X的標準差。
(2) 基于噪聲序列最大樣本熵的閾值估計應用
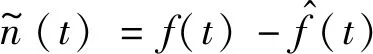
(11)
(12)
(3) 基于降噪序列最小樣本熵的閾值估計應用
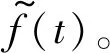
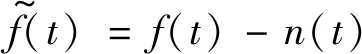
(13)
(14)
2.1.2 基于單樣本熵閾值估計方法的局限性
(1) 樣本熵值對噪聲集合完整度表征的影響
樣本熵值用于表征時間序列復雜度,卻無法描述序列集合的完整度,復雜度最大的噪聲序列并不一定是全部噪聲信號的完整集合。相反,完整集合的噪聲序列可能由于相似元素樣本量的增加導致樣本熵值下降。在降噪處理中,最大樣本熵值下的噪聲序列最復雜,可能不是全部噪聲的完整集合情況,所以根據噪聲序列最大樣本熵值估計得到的閾值存在保守、偏小的風險,得到的降噪信號去噪不完全。同樣的,基于降噪序列最小樣本熵估計閾值,隨著閾值增大降噪序列樣本熵降低,估計得到的閾值存在偏大的風險,使信號降噪程度過度加強,重構信號信息缺失。
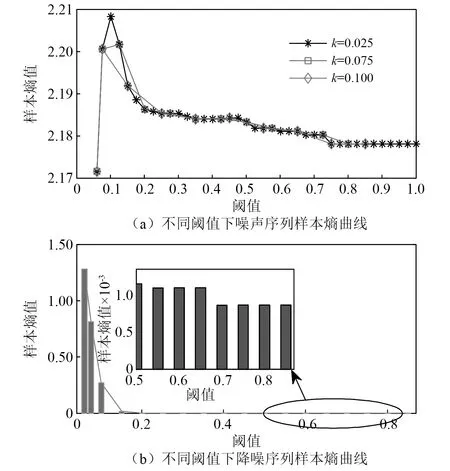
圖2 基于樣本熵極值的閾值估計模型Fig.2 Threshold estimation model based on sample entropy extreme value
以圖1(b)所示的局放單次脈沖含噪信號為試驗對象,噪聲估計信號和降噪估計信號的樣本熵曲線分別見圖2(a)和圖2(b)。按照最大熵原則選取閾值為0.101 0,在此閾值下對信號進行降噪,效果如圖3(a)所示,結果表明,基于噪聲序列最大樣本熵下的閾值進行小波降噪,得到的重構信號中仍然含有噪聲成分,降噪不完全;按照最小熵原則選取閾值為0.800 0,在此閾值下對信號進行降噪,效果如圖3(b)所示,結果表明,過度降噪造成重構信號故障信息缺失。
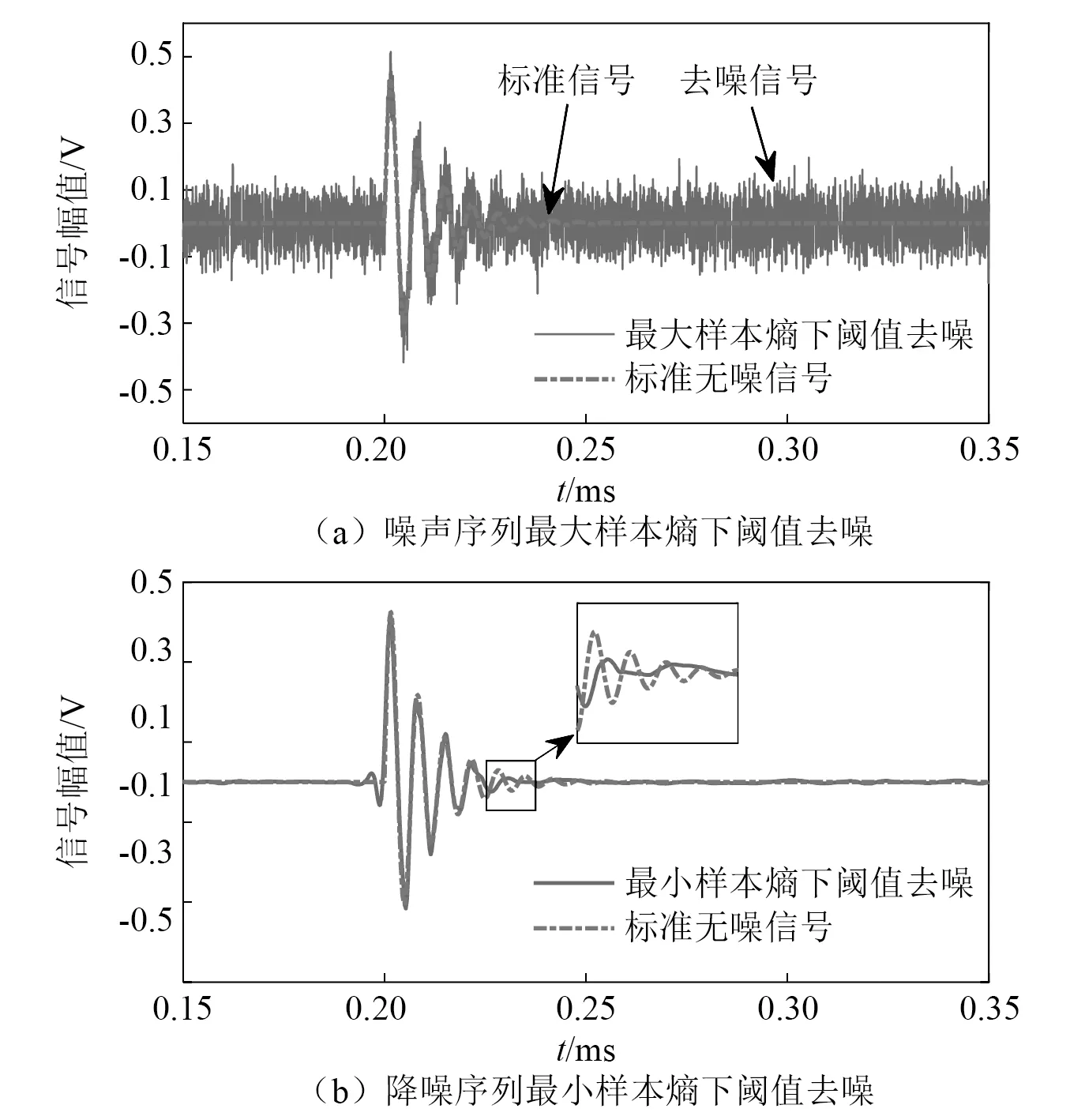
圖3 基于樣本熵極值下的閾值降噪效果Fig.3 Noise reduction effect based on the threshold under the extreme value of sample entropy
(2) 閾值步長對樣本熵極值搜索速度和精度的影響
在傳統樣本熵閾值估計算法中,閾值的慣性步長為一固定值,當步長設置過大時,容易影響全局搜索精度,使閾值估計值陷入局部最優;當步長設置過小時,會影響全局搜索速率,造成巨大計算資源消耗。針對圖1(b)所示的仿真信號,設置降噪閾值范圍為[0.01,1.01],不同步長下的最大樣本熵線性搜索結果如表1和圖2(a)所示。當閾值以步長k=0.025線性遞增時,獲得的樣本熵值曲線精度最高,但迭代次數最多,運算時間最長,最大樣本熵值的搜索速率低、計算負擔大;當閾值以步長k=0.100線性遞增時,運算時間變短,資源消耗相對減小,但搜索精度下降,得到的最大樣本熵值陷入了局部解。
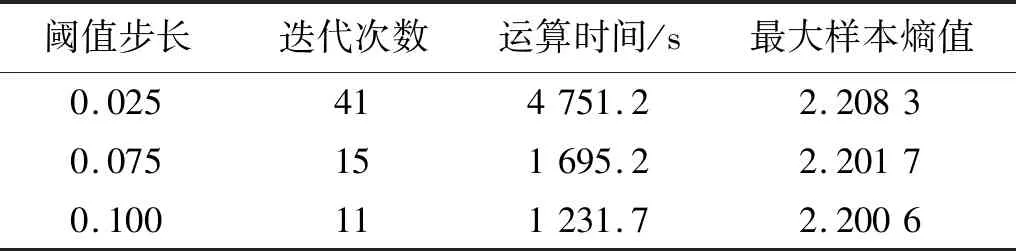
表1 不同步長下最大樣本熵線性搜索結果Tab.1 Linear search result of maximum sample entropy value under asynchronous length
2.2 綜合熵模型及其曲率拐點
針對上述2個局限性提出一種基于綜合熵的最優閾值快速估計方法。按照2.1.1節,選取樣本熵參數m=2,r=0.2std(X),計算降噪信號序列樣本熵值Sf,噪聲信號序列樣本熵值Sn,定義如式(15)所示的綜合熵(comprehensive entropy,CE)模型。
(15)
不同閾值作用下的降噪效果不一致,得到的綜合熵值也不同。在閾值域內,噪聲序列樣本熵值Sn先增后減,降噪序列樣本熵值Sf不斷減小,經過最優閾值節點后,信號降噪效果變化不明顯,樣本熵Sn和Sf值變化緩慢,使綜合熵Cλ值變化緩慢,研究認為最優閾值點位于綜合熵曲線變化走勢的拐點,稱其為曲率拐點Kmax。不同于單序列樣本熵最值估計問題,本文最優閾值的估計問題歸結為綜合熵曲率拐點的估計,如式(16)所示。
(16)
2.3 基于二分變步長非線性搜索的閾值快速估計
為了協調定步長線性迭代法存在的搜索精度與搜索速度的矛盾,本文引入非線性的慣性步長,采用二分變步長快速估計法,隨著搜索進行,步長逐漸縮小。搜索流程Ⅰ如圖4所示。首先,求解初始閾值對應的綜合熵曲率集;接著,以最大曲率對應閾值為中心,以二分閾值差為步長尋找中心域前后的閾值并考察其熵線曲率情況,不斷迭代逼近曲率拐點和最優閾值。值得說明的是,綜合熵是以信號處理后得到的降噪序列和噪聲序列為計算基礎,所以算法中需要提前確定閾值函數,而對于確定性序列,最優閾值往往是固定的,與閾值函數種類選取無映射關聯,為避免函數參量的影響,本文以硬閾值函數作為閾值尋優的試驗性函數,具體步驟如下:
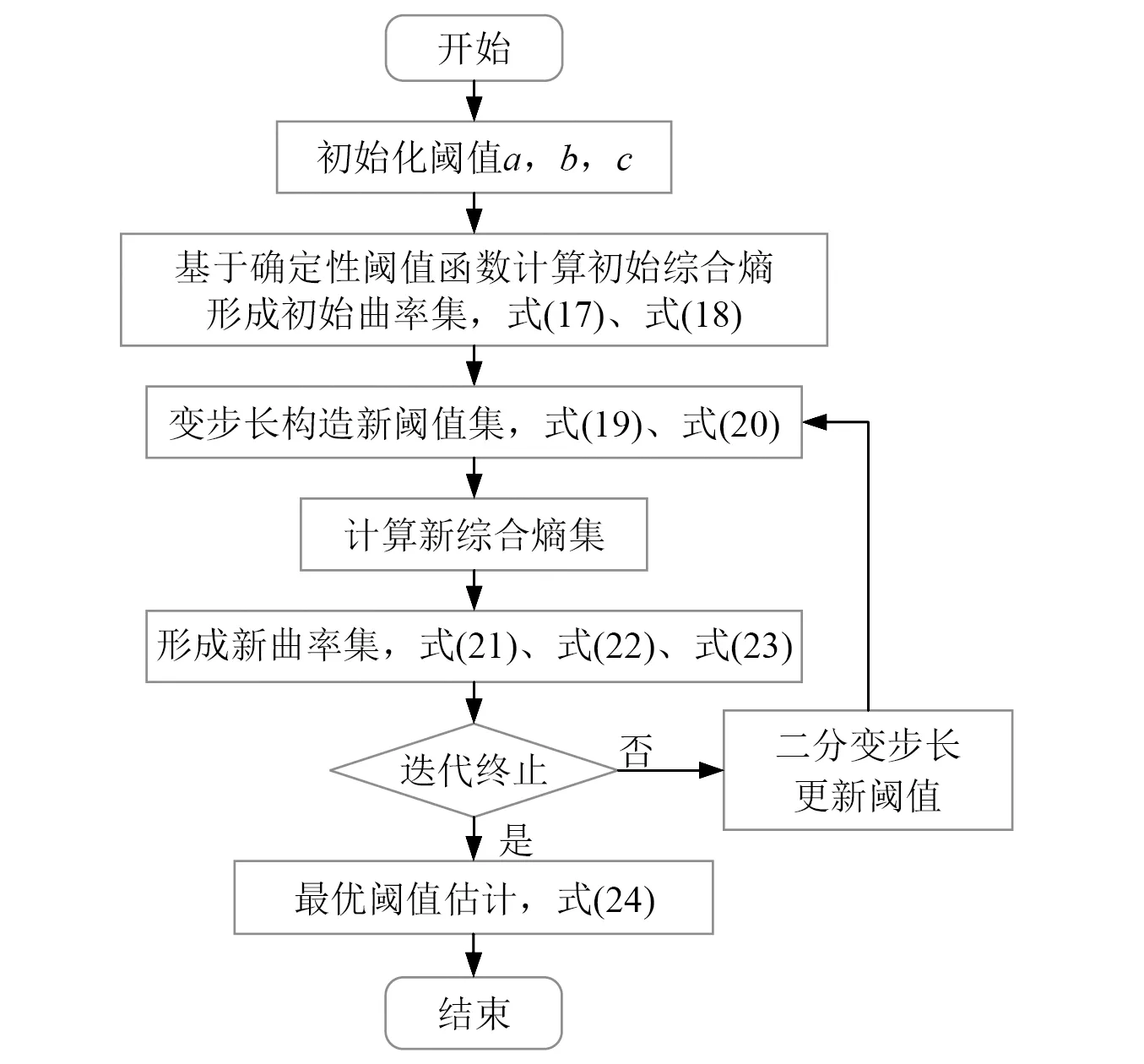
圖4 基于快速綜合熵的最優閾值估計(流程Ⅰ)Fig.4 Estimation of optimal threshold based on fast comprehensive entropy (Process Ⅰ)
步驟1設置閾值范圍λ?[a,c],迭代次數n,為使最優閾值有效地包含于該范圍中,λ的下限a應不大于“噪聲最大樣本熵法”得到的偏小估計值,上限c應不小于“降噪最小樣本熵法”得到的偏大估計值;
步驟2計算初始離散閾值域下的估計信號樣本熵,針對離散閾值集{a,b,c},b=(a+c)/2,基于試驗性函數估計各閾值下的降噪信號和噪聲信號,并計算其樣本熵值Sfa,Sna,Sfb,Snb,Sfc,Snc;
步驟3計算初始離散閾值域下的綜合熵曲率值,根據樣本熵計算閾值對應綜合熵Cza,Czb,Czc及其曲率Kb,Kc值,形成離散曲率集{Kb,Kc};
(17)
(18)
步驟4半步長構造新的離散閾值域,選擇當代最大曲率Kmax?{Kb,Kc}下對應的閾值b1,以b1為中心,閾值域b1的前位a1為首元素,(b1-a1)/2為步長構造新閾值a2,b2,順序形成下一代離散閾值集{a1,a2,b1,b2},若Kb=Kc,則取Kc下對應閾值b1為中心,(b1-a1)為步長構造新閾值;
(19)
(20)
步驟5考察新閾值集各元素對應曲率值,計算新一代各閾值下估計信號的樣本熵值Sfa1,Sna1,Sfa2,Sna2,Sfb1,Snb1,Sfb2,Snb2。進而計算a2,b1,b2閾值下綜合熵曲率值,形成新離散曲率域{Ka2,Kb1,Kb2};
(21)
(22)
(23)
步驟6終止迭代,判斷是否滿足迭代條件,若滿足則最大曲率值為估計曲率拐點,對應的閾值即為最優估計閾值,如式(24)所示;否則轉至步驟4基于半步長構造新一代離散閾值集,繼續考察新閾值處的曲率,不斷逼近最優閾值點。
(24)
3 改進閾值函數實現
3.1 經典閾值函數及改進
3.1.1 傳統閾值函數及其局限性
經典的小波閾值函數包括硬閾值函數和軟閾值函數,分別如式(25)和式(26)所示[21-25]。
(25)
(26)
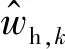
硬閾值函數表達如式(25)所示,將尺度系數絕對值與閾值比較,小于或等于閾值的系數置為0,大于閾值的系數保留不變,同閾值下的硬閾值函數降噪充分、效果明顯,但在正、負閾值處存在間斷的階躍點,使處理后的高頻尺度系數不連續,信號重構會產生振蕩。為此提出了如式(26)所示的軟閾值函數,尺度系數絕對值與閾值比較,小于或等于閾值的系數置為0,大于閾值的系數置為該點與閾值的差值,軟閾值函數實現系數在閾值處的連續性,抑制了重構信號振蕩,然而卻對系數的處理整體進行了收縮,重構信號較標準信號會存在恒定偏差。
3.1.2 改進閾值函數
(1) 改進閾值函數基本原理
針對上述軟、硬閾值函數存在的局限性,本文提出一種含參量的改進閾值函數,如式(27)所示。
(27)
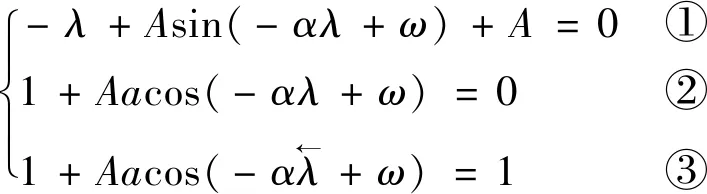
(28)
根據式(28)求得函數相關參數
(29)
(30)
(31)
一般取k1=k2=0,假設某閾值為5,根據式(27)~式(31),所提改進函數模型如圖5所示。
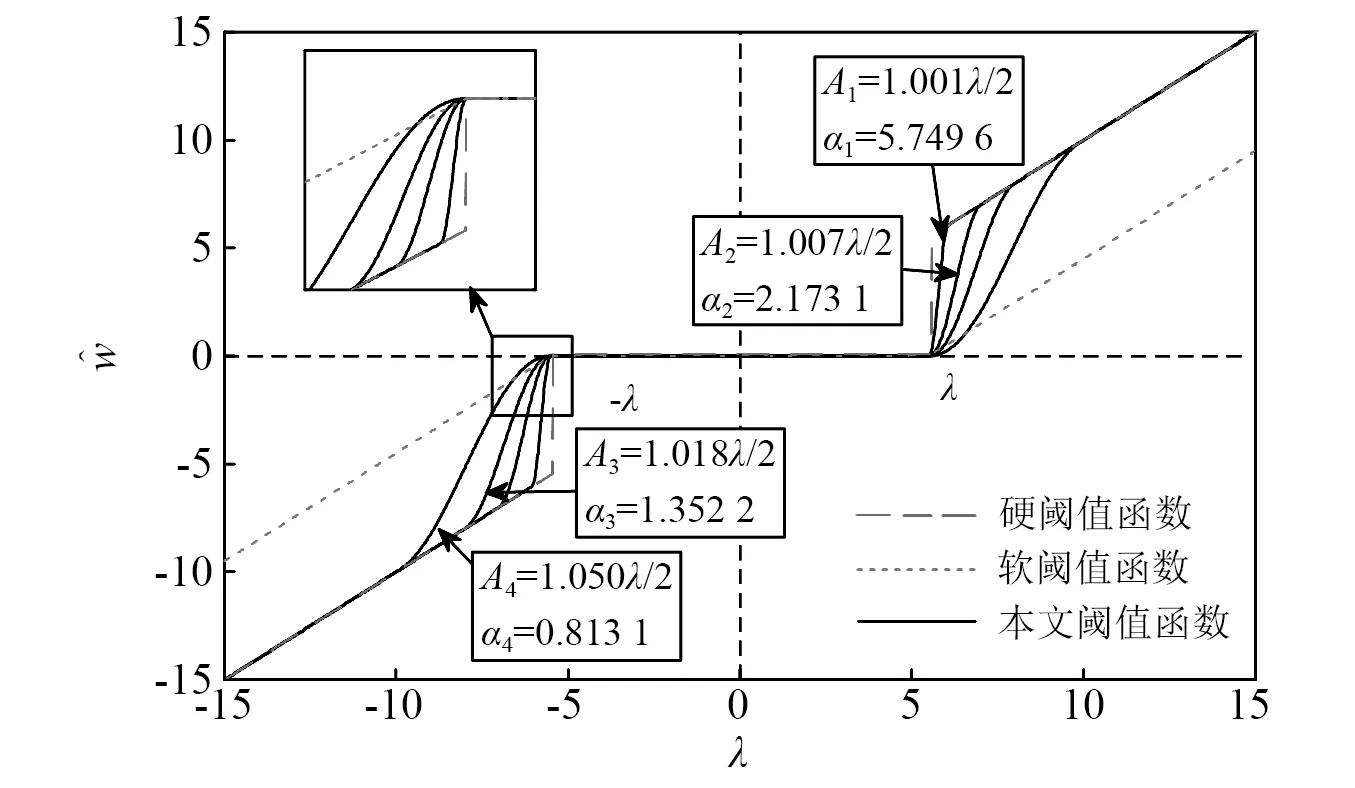
圖5 改進閾值函數模型Fig.5 Improved threshold function model
(2) 改進閾值函數特點
1) 連續性討論——在函數左半支對閾值點和前向閾值點處函數連續性討論如下:
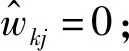
2) 可導性討論——在函數左半支對閾值點和前向閾值點處函數可導性討論如下:
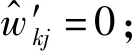
改進函數為關于原點對稱的奇函數,右半支函數同樣具有連續可導性。綜上,所提改進閾值函數在全閾值域內具有連續可導性。
3.2 基于平滑過渡數的函數參數選擇方法
改進閾值函數具有一個可調節的品質因子α參量(見圖5)。α值不會對函數的連續性與可導性產生影響,但決定了其他參量的取值,不同α下得到的改進函數不同,一定程度上約束了降噪效果和重構信號的品質,根據式(29),α可由式(32)估計得到
(32)
由式(32)可知,函數閾值幅度A越小,品質因子α值越大,函數越接近硬閾值函數特性,A越大,α值越小,函數越接近軟閾值函數特性,在閾值點不發生漂移的情況下,通過調整α值實現改進函數向軟、硬閾值函數平滑過渡和繼承。為快速完成對參量α的選擇,本文建立平滑過渡數模型,定義硬過渡數Ph和軟過渡數Ps表達式用以刻畫函數軟、硬化程度。
(33)
(34)
Ph+Ps=1
(35)
硬過渡數Ph和軟過渡數Ps取值范圍為0~100%,當閾值幅度A=λ/2時,過渡數Ph=1,Ps=0,表明函數100%繼承硬閾值函數特性,代入式(32)中可得α趨于無窮大;當閾值幅度A=λ時,過渡數Ph=0,Ps=1,表明函數100%繼承軟閾值函數特性,此時α=1/λ。
基于平滑過渡數的參數選擇示例:設置硬過渡數Ph=99.6%,軟過渡數Ps=0.4%,根據式(33)~式(35)有A=1.004λ/2;代入式(32)中得α≈1/0.063λ,閾值λ由最優閾值估計法獲取;基于α值,根據式(30)和式(31)計算其余參量,最終得到改進閾值函數,流程Ⅱ如圖6所示。
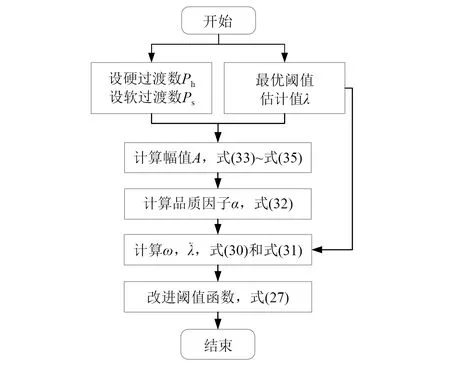
圖6 改進閾值函數參數計算(流程Ⅱ)Fig.6 Improve the parameter calculation of the threshold function(Process Ⅱ)
4 基于改進閾值估計和改進閾值函數降噪方法
4.1 改進降噪方法過程概述
基于快速綜合熵改進最優閾值估計和改進小波閾值函數實現對信號st的降噪過程,如圖7所示,具體步驟如下:
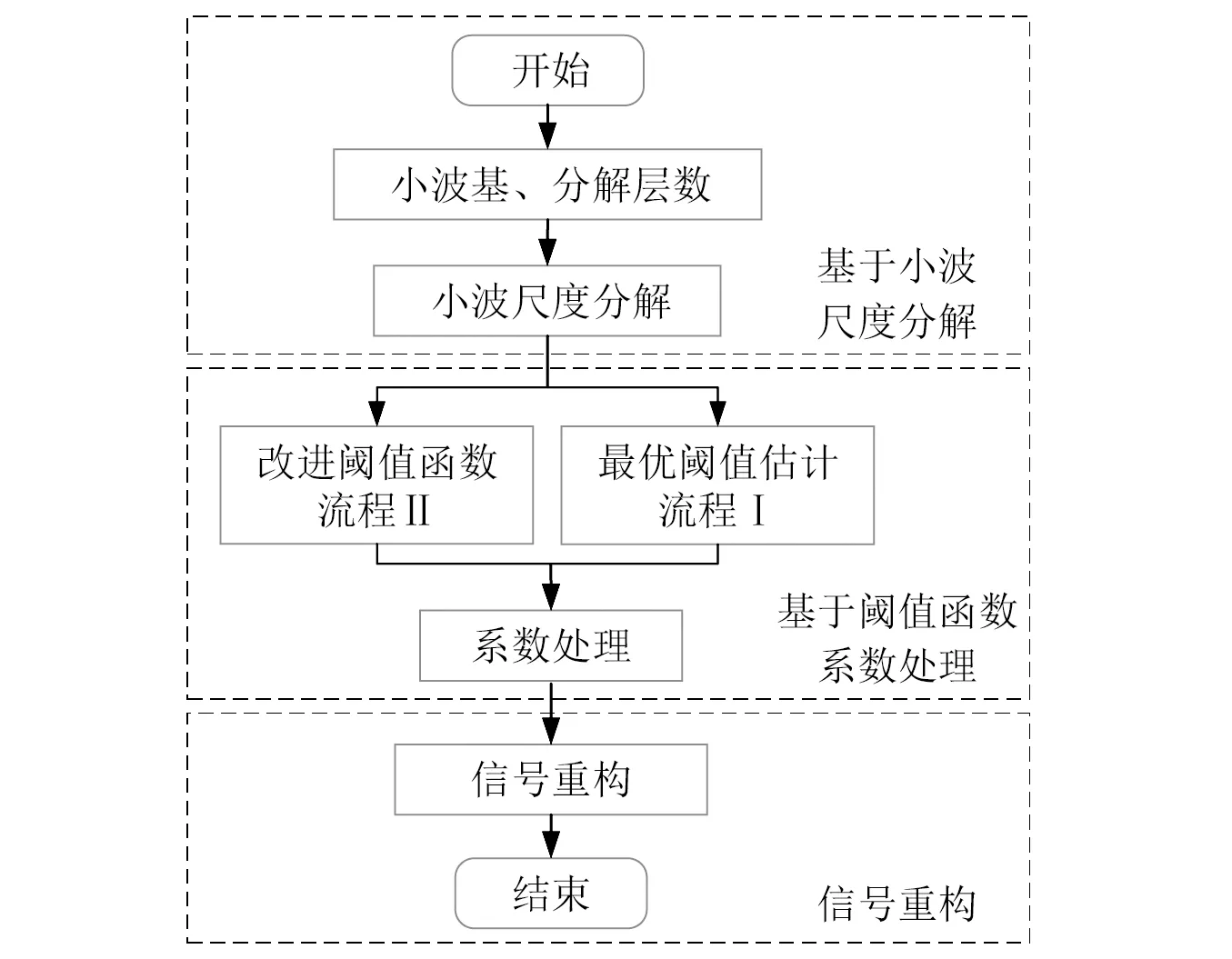
圖7 基于改進閾值估計和閾值函數的信號降噪過程Fig.7 Signal denoising process based on improved threshold estimation and improved threshold function
步驟1根據信號特性選取合適的小波基,確定信號分解層數,對含噪信號st進行小波尺度分解,得到低頻系數與高頻系數;
步驟2根據第2章,基于二分變步長非線性搜索法快速估計序列綜合熵曲率拐點,得到估計最優閾值λ;根據第3章,基于平滑過渡指數模型完成函數參數選擇,得到改進閾值函數;
步驟3基于最優閾值估計值λ和改進閾值函數,對高頻系數進行處理,得到降噪后的高頻系數;
步驟4基于分解的低頻系數與閾值處理后的降噪高頻系數進行小波重構,得到降噪后的信號。
4.2 降噪效果性能評估指標
為了驗證本文改進小波閾值方法的有效性,選擇信噪比(signal-noise ratio,SNR)、均方根誤差(root mean square error,RMSE)和皮爾遜相關系數(Pearson correlation coefficient,PCC)作為降噪效果評價指標,降噪后信號與標準信號的SNR越大,RMSE越小,PCC越大,表明降噪信號與標準信號相關度越好,降噪效果越好。
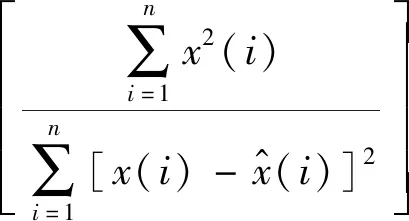
(36)
(37)
(38)
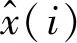
5 基于改進閾值估計和改進閾值函數降噪實例
5.1 實例一:基于MATLAB實驗室的局部放電超聲波仿真信號降噪應用
5.1.1 平臺環境與小波分解預處理
基于MATLAB實驗室環境搭建如圖1(b)和圖1(c)的含噪局放超聲波脈沖仿真信號,按照文獻[26]的方法基于互相關系數實現信號分解的小波基和分解層數優化選擇,分別計算不同db小波基(db2~db10)、不同分解層數(4層~11層)下降噪信號與標準信號的互相關系數值,以互相關系數最大值為目標優化選擇小波分解參數,試驗結果如圖8所示。圖8(a)表明,不同小波基函數下降噪效果不一致,得到的互相關系數值也不同;圖8(b)表明,隨著分解層數的增加,信號分辨率愈高,降噪效果愈好,互相關系數值增大,當超過最優分解層后,降噪效果提升不明顯甚至呈下降趨勢。根據試驗結果,針對單次局部放電超聲波仿真信號,小波參數選取為互相關系數值最優的db6小波、9層分解;針對周期局部放電超聲波仿真信號,則選取db5小波、7層分解。
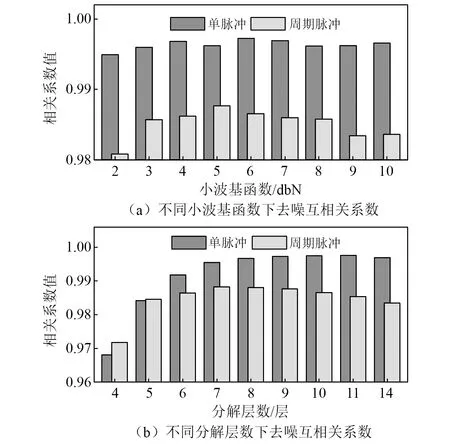
圖8 基于互相關系數的小波基和分解層數選取試驗Fig.8 Experiment on the selection of wavelet basis and decomposition level based on PCC
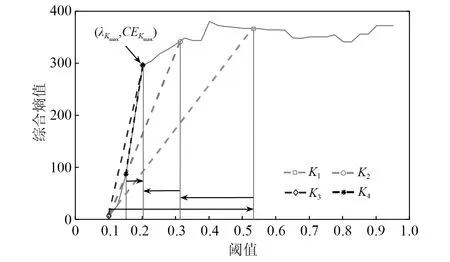
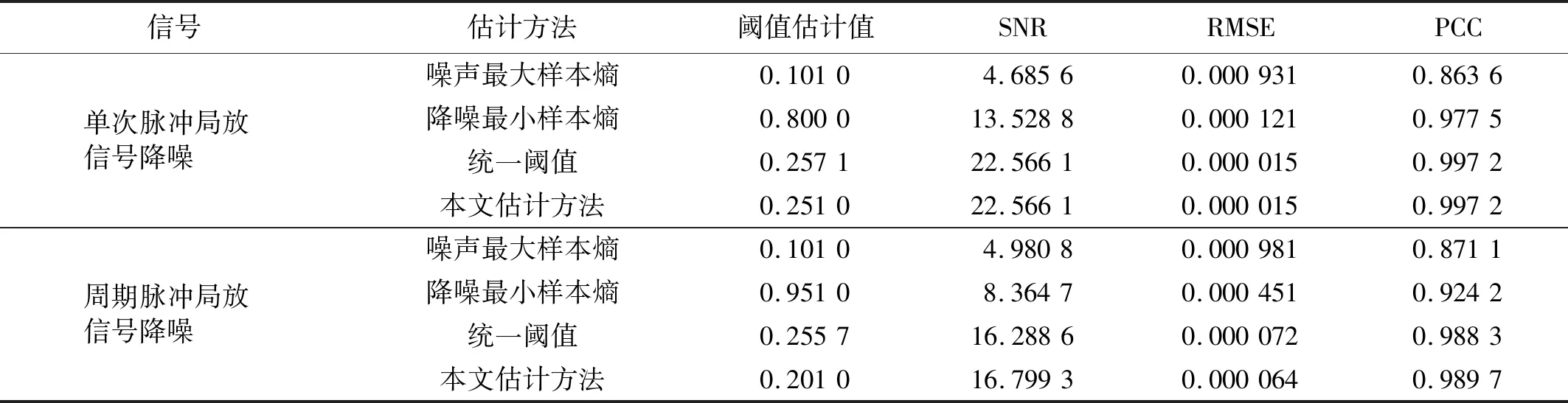
5.1.2 最優閾值估計試驗
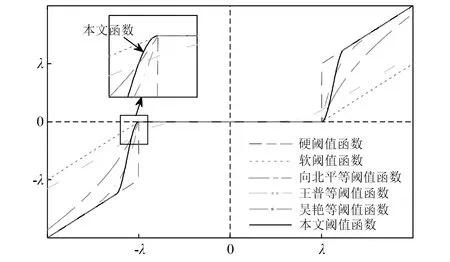
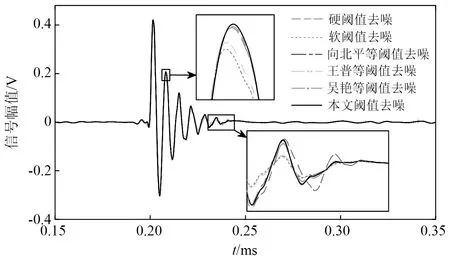
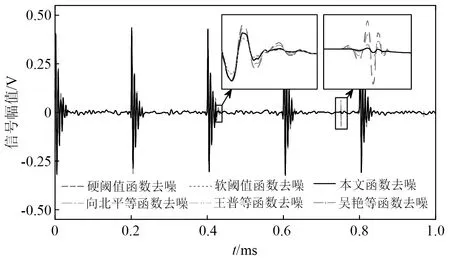
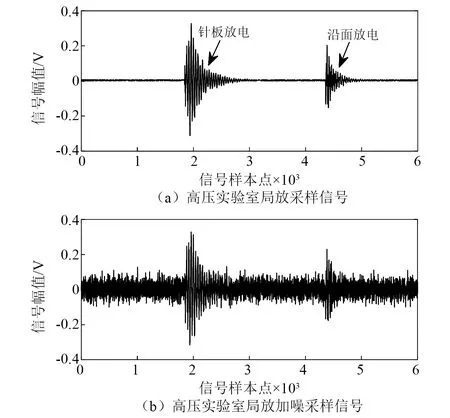
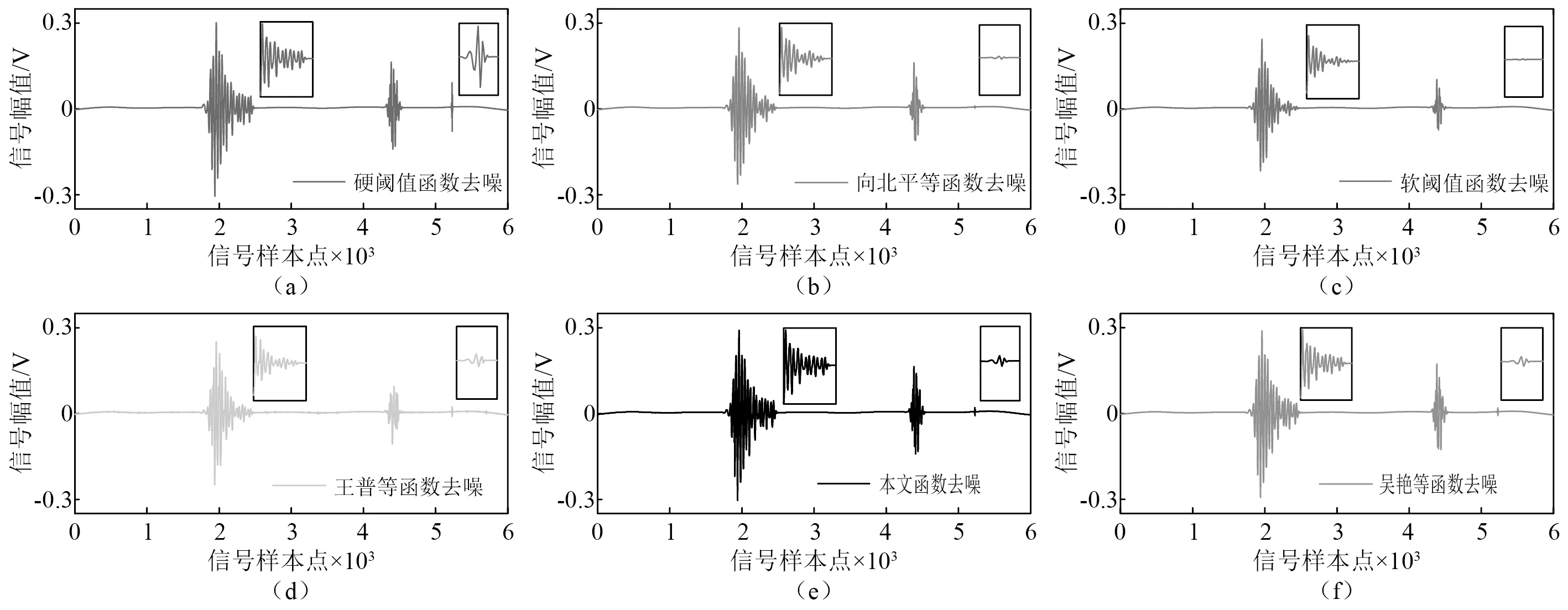
針對局放超聲波脈沖仿真信號,表2列出了各種方法下的閾值估計值。由表2可知:單脈沖工況下噪聲最大樣本熵法估計的偏小閾值為0.101 0,降噪最小樣本熵法估計的偏大閾值為0.800 0,根據閾值范圍選取原則(見2.3節),可設λ?[0.101 0,0.800 0],其綜合熵曲線如圖9所示;周期脈沖工況下閾值估計偏小值為0.101 0,偏大值為0.951 0,可設λ?[0.101 0,0.951 0],其綜合熵曲線如圖10所示。對曲率拐點的搜索,若采用小步長慣性迭代,搜索次數和計算負荷增大;若采用大步長慣性迭代則會導致搜索精度下降。本文所提的二分變步長非線性搜索法的尋優過程如圖9和圖10中矢量箭頭所示,5次搜索的熵曲率值大小為K1 為驗證所提快速閾值估計方法的有效性,分別與噪聲序列最大樣本熵閾值估計法、降噪序列最小樣本熵閾值估計法、經典統一閾值估計法[27]進行對比,不同估計方法下估計閾值的降噪效果見表2。由表2可知:不論是單脈沖還是周期脈沖的局放超聲波信號,基于噪聲序列最大樣本熵估計的閾值相對最小,由于小閾值作用信號使噪聲處理不完全,降噪后信號的SNR值相對最小,RMSE值相對最大,PCC值相對最小,降噪效果最不理想;而基于降噪序列最小樣本熵估計的閾值由于偏大而產生過度降噪,得到的降噪信號與標準信號仍然存在偏差;經典的統一閾值估計法簡單快速,但估計得到的閾值存在偏大風險,對于復雜的周期脈沖信號降噪效果不明顯;本文所提二分變步長非線性搜索法尋優收斂速度快、精度高,估計閾值作用下降噪信號的SNR值最大,RMSE值最小,PCC值最大,獲得了良好的信號降噪效果。 圖9 基于綜合熵的最優閾值估計(針對單次局放信號)Fig.9 Optimal threshold estimation based on comprehensive entropy(For a partial discharge signal) 圖10 基于綜合熵的最優閾值估計(針對周期局放信號)Fig.10 Optimal threshold estimation based on comprehensive entropy(For periodic partial discharge signal) 表2 不同閾值估計方法下的超聲波仿真信號降噪Tab.2 Noise reduction of ultrasonic simulation signal under different threshold estimation methods 5.1.3 改進閾值函數降噪試驗 為驗證所提改進閾值函數降噪方法有效性,針對局放超聲波脈沖仿真信號,分別采用硬閾值函數、軟閾值函數、向北平等、王普等、吳艷等所提改進閾值函數和本文改進閾值函數降噪方法進行對比,各閾值函數模型如圖11所示。按照參數選擇方法,設置硬過渡數Ph=99.96%,軟過渡數Ps=0.04%,得到A=1.004λ/2,α≈1/0.063λ,根據表2,兩種仿真信號的最優估計閾值λ分別取0.251 0,0.201 0,其中各閾值函數降噪得到的重構信號如圖12、圖13所示,降噪效果如表3所示。 圖11 各閾值函數模型對比Fig.11 Comparison of various threshold function models 圖12 基于改進閾值函數的信號降噪(針對單次局放信號)Fig.12 Signal noise reduction based on improved threshold function (For a partial discharge signal) 圖13 基于改進閾值函數的信號降噪(針對周期局放信號)Fig.13 Signal noise reduction based on improved threshold function (For periodic partial discharge signals) 表3 不同閾值函數方法下的超聲波仿真信號降噪Tab.3 Noise reduction of ultrasonic simulation signal under different threshold function methods 由圖11可知,幾種改進閾值函數均介于軟、硬閾值函數之間,試驗結果表3表明,相對于未去噪情況,所有降噪方法均有效提升了SNR值和PCC值,降低RMSE值,參數約束域內的降噪效果為:軟閾值<王普等<向北平等<吳艷等<本文<硬閾值函數降噪方法。 由表3可知:硬閾值函數降噪的SNR值和PCC值最大、RMSE值最小,降噪效果顯著,然而圖13所示結果表明此方法在0.75 ms左右處重構信號時出現了振蕩缺陷;軟閾值函數在閾值域內連續,有效抑制了重構振蕩,但圖12所示結果表明此方法在信號脈沖波峰處與標準信號存在恒定偏差,SNR值和PCC值較小、RMSE值較大,降噪效果有待提升;王普等所提函數特性最接近軟閾值函數,較其他改進方法其降噪效果提升不明顯;向北平等和吳艷等所提函數連續且接近硬閾值函數,降噪效果提升有效,但在閾值鄰域內存在函數不可導、系數過渡不平滑的局限性;而本文改進閾值函數在參數約束域內較其他改進方法SNR值和PCC值較大,RMSE值較小,降噪效果最好,對單脈沖、周期脈沖局放超聲波信號均具有良好的降噪適應性。 5.2.1 平臺環境與小波分解預處理 高壓電力設備在不同結構、不同區域處發生局部放電使絕緣缺陷類型多樣化,其中沿面放電、針板放電是兩種經典的局放類型[28]。基于高電壓實驗室搭建模擬這兩類局部放電的試驗場景,接線如圖14所示,220 V 交流電源接入電源控制箱,控制變壓器產生最高100 kV的高電壓,有效滿足高壓放電的要求,放電模型一端加載高壓,另一端通過地線接入大地,試驗用超聲波傳感器置于金屬支撐板完成信號捕捉,示波器用以傳感器信號接入與觀察。 圖14 基于高電壓實驗室的局部放電模擬試驗Fig.14 Partial discharge simulation experiment based on high voltage laboratory 本文高壓局放試驗中控制產生35 kV等級的高電壓,并分別加載在針板放電和沿面放電模型上,傳感器捕捉放電產生的超聲波信號,整理后獲得6 000個兩類局放信號采樣序列點,如圖15(a)所示,人工加噪后的局放超聲波信號如圖15(b)所示。對于該類型試驗信號,按照單脈沖局放仿真信號分解方法,選取db6作為小波基函數,信號分解層數設置為9層較為合適。 5.2.2 最優閾值估計試驗 針對含噪局放試驗超聲波脈沖信號,表4列出了各種方法的閾值估計值。由表4可知,噪聲最大樣本熵法估計的偏小閾值為0.074 0,降噪最小樣本熵法估計的偏大閾值為0.181 0,根據閾值范圍選取原則(見2.3節),可設λ?[0.074 0,0.181 0]。基于本文非線性搜索法估計最優閾值,尋優過程如圖16中矢量箭頭所示,經過8次快速搜索后的綜合熵曲率值如圖16所示,得到最優估計閾值為0.151 0。 圖15 局部放電超聲波試驗信號Fig.15 Partial discharge ultrasonic experimental signal 圖16 基于綜合熵的最優閾值估計(針對局放試驗信號)Fig.16 Optimal threshold estimation based on comprehensive entropy (For partial discharge experimental signal) 以圖15(a)所示信號為標準信號,采用多個閾值估計方法進行對比試驗,結果見表4。由表4可知:基于噪聲序列最大樣本熵估計的閾值較為保守,降噪后信號的SNR值和PCC值相對最小,RMSE值相對最大,降噪效果相對最差;基于降噪序列最小樣本熵估計法和經典統一閾值估計法得到的閾值存在偏大風險,降噪效果并非最優;而基于本文所提二分變步長非線性搜索法估計閾值相對最優,降噪后信號的SNR值和PCC值最大,RMSE值最小,降噪效果相對最優。 5.2.3 改進閾值函數降噪試驗 為驗證所提改進閾值函數對局放超聲波信號降噪的工程應用性,仍然采用如圖11所示的硬閾值函數、軟閾值函數、向北平等、王普等、吳艷等所提閾值函數和本文閾值函數降噪方法進行對比,根據表4最優閾值λ取0.151 0。其中各閾值函數降噪方法的重構信號如圖17所示,各閾值函數下降噪效果如表5所示。 表4 不同閾值估計方法下的超聲波試驗信號降噪Tab.4 Denoising of ultrasonic experimental signals under different threshold estimation methods 圖17 局部放電超聲波試驗信號降噪Fig.17 Partial discharge ultrasonic experiment signal noise reduction 表5 不同閾值函數方法下的超聲波試驗信號降噪Tab.5 Denoising of ultrasonic experimental signals under different threshold function methods 由表5可知,在硬閾值函數降噪方法下由于降噪充分,重構信號的SNR值和PCC值最大,RMSE值最小,降噪效果相對最優。圖17表明,該函數作用降噪重構信號保留了較為完整的脈沖波峰信息,但在5 300左右采樣點處存在重構振蕩現象,會對下一階段的局放故障識別與處理造成信息干擾。而軟閾值函數去噪能有效地抑制振蕩現象,但由于對尺度系數的收縮處理,重構信號的脈沖幅值被消減,脈沖波峰信息完整性缺失,降噪效果不理想,同樣會對故障識別與處理造成信息干擾。表5表明,向北平等、王普等和吳艷等改進方法的降噪效果并非最優,而本文改進閾值函數在抑制重構振蕩的同時最接近硬閾值函數降噪品質,保留了較為清晰完整的故障信息,相較其他改進函數,本文所提改進函數具有良好的降噪充分性。 文中提出一種基于改進最優閾值估計和改進閾值函數的小波閾值降噪優化方法,并實現高壓電力設備局部放電超聲波信號降噪應用,通過仿真及試驗驗證,得出如下結論: (1) 在融合噪聲序列和降噪序列樣本熵信息基礎上,建立綜合熵模型,以綜合熵曲率拐點對應的閾值為最優閾值,克服了單序列樣本熵極值估計閾值存在局部解的情況。同時提出二分變步長非線性閾值搜索法,有效地協調了傳統定步長閾值搜索存在搜索速度和精度的矛盾。試驗結果表明,所提搜索方法較傳統方法具有顯著的搜索速度和精度優勢。 (2) 提出了介于軟、硬閾值函數之間的改進閾值函數,該函數具有全閾值的連續可導性,通過定義的平滑過渡數模型Ph和Ps實現函數參數快速選擇,優化所提函數從軟特性到硬特性的繼承和過渡。 (3) 基于MATLAB實驗室與高電壓實驗室分別將改進方法應用于單次局放與周期局放信號,針板局放與沿面局放信號降噪場景。結果表明,所提降噪方法有效地繼承了軟、硬閾值函數優勢,在抑制重構振蕩的同時具有降噪充分性,重構信號保留了較為完整的故障信息。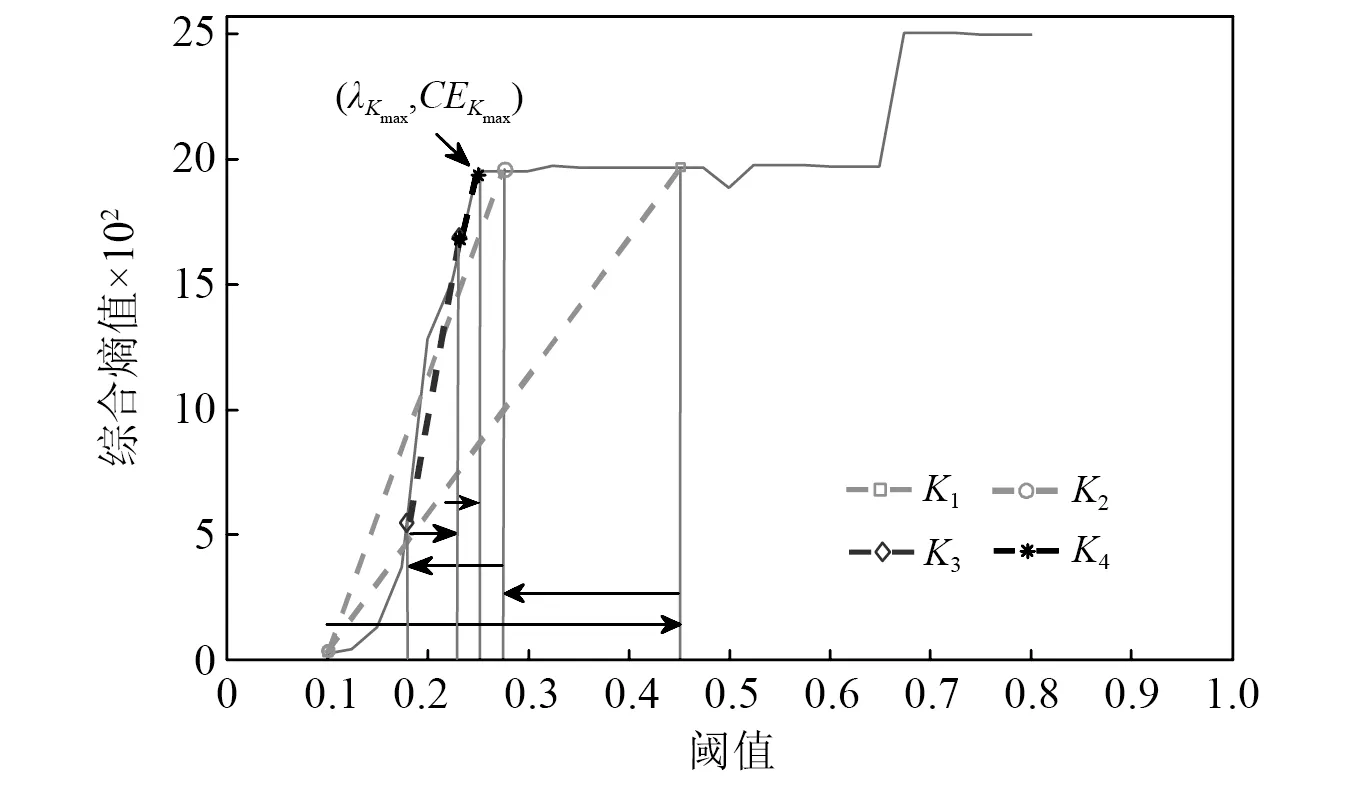

5.2 實例二:基于高電壓實驗室的局部放電超聲波試驗信號降噪應用




6 結 論

