基于不同截面形狀的螺旋彈性管束換熱器傳熱特性分析

季家東，周 蓉，高潤淼，張經緯，鄧 旭，李飛揚

(1.安徽理工大學 機械工程學院，安徽 淮南 232001；2.安徽理工大學 人工智能學院，安徽 淮南 232001)

振動強化傳熱無需消耗額外能量，屬于無源強化傳熱技術[1-2]，是換熱器研發、設計領域的主要內容之一。彈性管束換熱器是一種利用振動實現強化傳熱的典型設備，其利用紫銅元件替代傳統不銹鋼元件，在保證使用壽命的同時，大幅提高傳熱性能。與傳統平面彈性管束不同[3-4]，螺旋彈性管束便于在換熱器內實現順/逆向密集布置，有利于換熱器的總體傳熱性能的提高[5]。螺旋彈性管束的截面形狀改變，會影響換熱器內殼、管程流體的流動特性，進而影響螺旋管束的振動和傳熱特性。因此，基于管束的不同截面形狀，研究螺旋彈性管束的傳熱性能，對于螺旋彈性管束換熱器的設計和研發具有重要的理論和工程意義。

關于傳統彈性管束及其換熱器，大量科研人員[6-11]基于流體誘導振動、振動強化傳熱、管束結構改進等方面進行了許多卓有成效的研究。研究表明：傳統彈性管束在低流速流體誘導下振動強化傳熱效果明顯，且流體誘導振動的主因為殼程流體，振動主要表現為垂直于管束平面的面外振動。關于螺旋彈性管束換熱器，Wu等[12]通過對一種螺旋管束換熱器在殼程流體誘導下綜合性能的研究發現：由于大量渦流的存在，增強了殼程流體的湍流特性，進而提高了換熱器的綜合傳熱性能。Ji等通過對換熱器內單層雙螺旋彈性管束傳熱性能的研究發現：螺旋管束的振動主要表現為垂直方向，換熱器內上部管束的平均傳熱系數比下部管束的平均傳熱系數高約2.2倍。Khosravi-Bizhaem等[13]通過研究螺旋管中脈動流對傳熱特性的影響發現：在脈動流作用下，壓降增加了3%～7%，換熱性能提高了約39%。關于截面形狀方面，Su等[14]基于三種截面形狀對管束渦激振動特性和傳熱機理進行了研究，研究發現：在較低流速下，漩渦脫落力影響水平橢圓管的振動特性；當流體速度較大時，局部壁面渦流使得局部換熱系數明顯提高。

為探究截面形狀對螺旋彈性管束傳熱性能的影響，本文以螺旋彈性管束四種截面形狀(四邊形、六邊形、橢圓形和圓形)為出發點，以雙向流固耦合(fluid structure coupling，FSC)計算的順序求解法為基本手段，對單層四螺旋彈性管束在不同入口速度條件下的振動和傳熱特性進行了研究。

1 數值計算方法

1.1 螺旋彈性管束

單層四螺旋彈性管束換熱器示意圖，如圖1所示。

圖1 螺旋彈性管束換熱器Fig.1 Spiral elastic tube bundle heat exchanger

如圖1所示，四根尺寸一致的螺旋彈性管束等間距的安裝在換熱器左右管板上，管程熱流體從左側管程入口流入換熱器左封頭區域，通過左管板孔流入四根螺旋彈性管束，經右管板孔流入換熱器右封頭區域，從右側管程出口流出。殼程冷流體從底部殼程入口流入換熱器內部，沖刷螺旋彈性管束后從頂部殼程出口流出。冷熱流體相互作用，耦合誘導螺旋彈性管束振動，進而實現強化傳熱。

1.2 流體域和結構域

圖2所示為螺旋彈性管束流體域及結構域。因殼程流體為管束振動的主因，計算僅保留殼程流體。圖2中：L為流體域或螺旋管長度；P為螺距；Dh為螺旋直徑；M為殼程出、入口距離流體域左、右端間距；R1為殼程出、入口流體域半徑；R2為流體域半徑。為便于說明，將管束編號為1～4，并標記為i(i=1～4)。此外，為分析管束截面圓周的局部傳熱性能，選取四個截面位置為分析對象(圖示Ⅰ、Ⅱ、Ⅲ、Ⅳ)，編號與管束編號相對應。

計算過程中，結構參數設置如下：L=600 mm，P=100 mm，Dh=100 mm，M=30 mm，R1=20 mm。為便于對比，不同截面形狀的管束設置相同的壁厚(δ=1.0 mm)和相同的截面積(S=78.5 mm2)。

螺旋彈性管束的材料為紫銅，物性參數為：密度ρp=8 900 kg/m3，彈性模量Ep=1.29×1011Pa，泊松比υp=0.33。

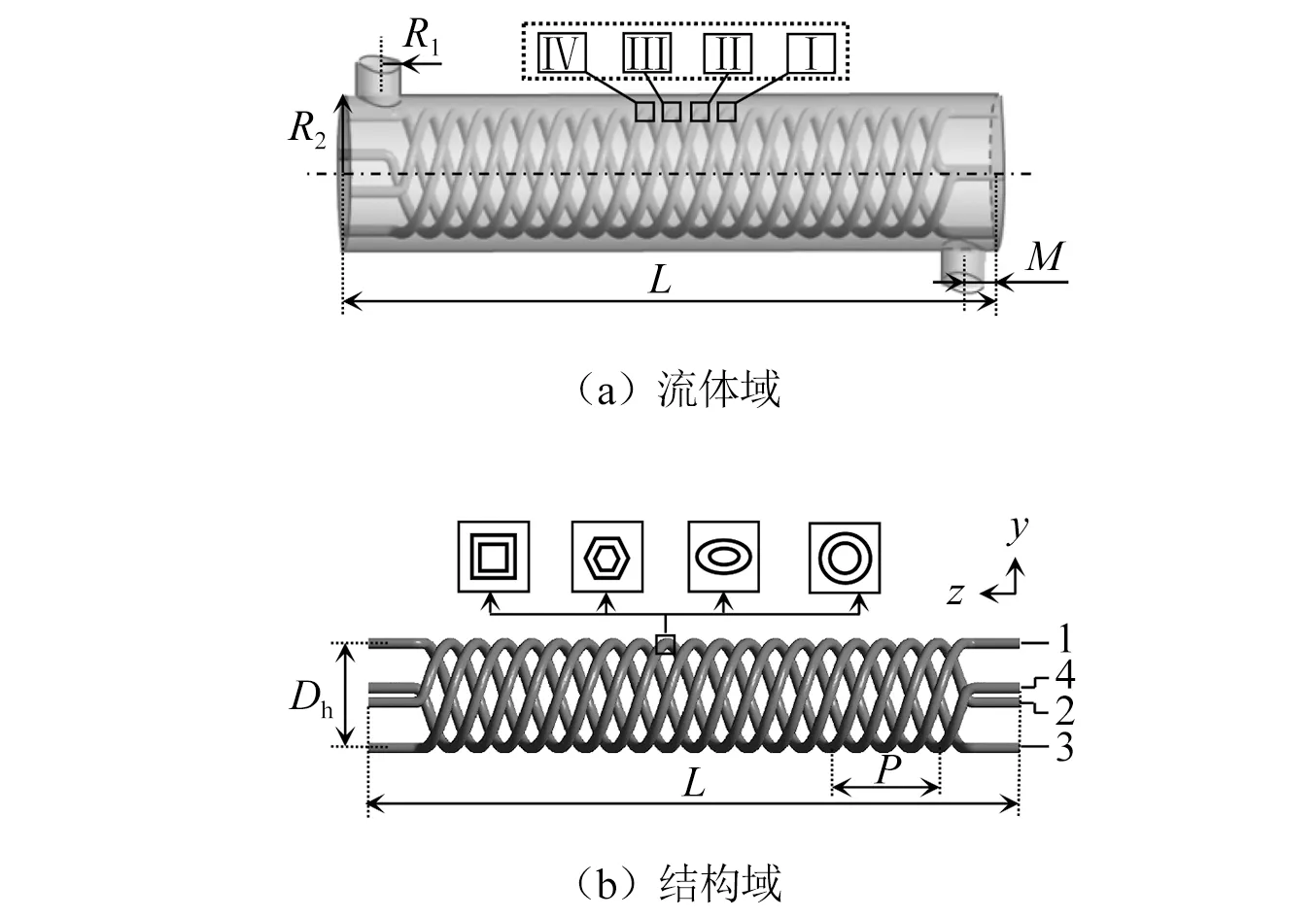
圖2 流體域和結構域Fig.2 Fluid domain and structural domain

1.3 數值方法

計算過程中，流體介質為不可壓縮流體——水。熱物性參數取決于流體平均溫度，且不考慮熱損失。流體域計算采用ANSYS CFX軟件，結構域計算采用ANSYS Workbench平臺的Transient Structural模塊。流體域邊界設置：入口設置為“Inlet”，給定入口流體速度(vin=0.1 m/s，vin=0.4 m/s，vin=0.7 m/s)和溫度(Tin=293.15 K)；出口設置為“Outlet”，給定出口 相對壓力(Pre=0)；設置與管束接觸的壁面為FSC交界面，給定壁面溫度(Twall=333.15 K)。結構域邊界條件：螺旋彈性管束的兩端面均設置為“Fixed Support”；螺旋彈性管束的壁面均設置為FSC交界面，對應于流體域的FSC交界面；設置重力加速度方向為-y方向，其值為：9.807 m/s2。

基于考慮FSC交界面的能量損失，系統有限元波動方程為

(1)

基于哈密爾頓原理，含流體力的結構力學方程為

(2)

式中：下標f為流體；下標p為結構；M，C，K分別為質量、阻尼和剛度矩陣；u為速度矢量；p為流體動壓；RT為FSC交界面的耦合矩陣；Fp和Ff分別為結構場內部作用力和流體作用力。

聯立式(1)和式(2)，可得FSC問題的有限元離散方程為

(3)

FSC計算時，流體域和結構域的數據傳遞通過FSC交界面實現，且遵循如下守恒

nfτf=npτp

(4)

sf=sp

(5)

式中：n為FSC交界面的法向矢量；τ為FSC交界面的壓力；s為FSC交界面的位移。

計算滿足如下條件時，計算結束。

(6)

為得到穩定流場的傳熱數據，將計算過程分兩步進行：粗算和精算。粗算：基于流場初始邊界條件，啟動CFX解算器對流體域進行計算，直至殼程流場獲得充分發展。精算(計算流程見圖3)：① 以粗算后流場條件為初始條件，啟動CFX解算器對流體域進行第一步計算，將計算后的壓力通過FSC交界面傳遞到結構域；② 以FSC交界面傳遞的流體力為初始條件，結合結構域初始邊界條件，啟動ANSYS解算器對結構域進行第一步計算，將計算后的位移通過FSC交界面傳遞到流體域；③以FSC交界面傳遞的位移為初始條件，結合第一步計算的流場條件，啟動CFX解算器對流體域進行第二步計算，將計算后的壓力通過FSC交界面再次傳遞到結構域；④ 以FSC交界面傳遞的流體力為初始條件，結合結構域第一步計算的結果，啟動ANSYS解算器對結構域進行第二步計算，將計算后的位移通過FSC交界面再次傳遞到流體域；⑤ 如此交替計算，直至完成所有時間步。

圖3 FSC計算(精算)流程Fig.3 Process of FSC calculation (accurate calculation)

粗算過程中，為使流場獲得充分發展，設置計算時間為300 s，時間步長為0.1 s。經驗證，該時間及步長設置能夠使本文計算流速條件下(vin=0.1 m/s，vin=0.4 m/s，vin=0.7 m/s)的流場獲得充分發展。精算過程中，為捕捉到精確的振動波，設置計算時間為1.2 s，時間步長為0.001 s。經驗證，該時間及步長設置滿足計算要求(參見1.5節結果驗證)。

1.4 網格劃分

圖4所示為流體域和結構域網格，網格劃分采用ANSYS Workbench平臺的Meshing模塊執行。結構域劃分為六面體網格，流體域劃分為四面體網格，且流體域內部近壁區設置6層邊界層網格。

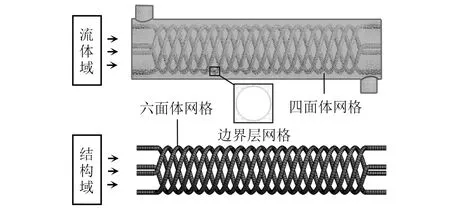
圖4 流體域和結構域網格Fig.4 Grids of fluid domain and structural domain

基于不同截面形狀的流體域和結構域的網格數和節點數，如表1所示。經試算，進一步增加網格數目和邊界層數對計算結果的影響不大，網格滿足獨立性。

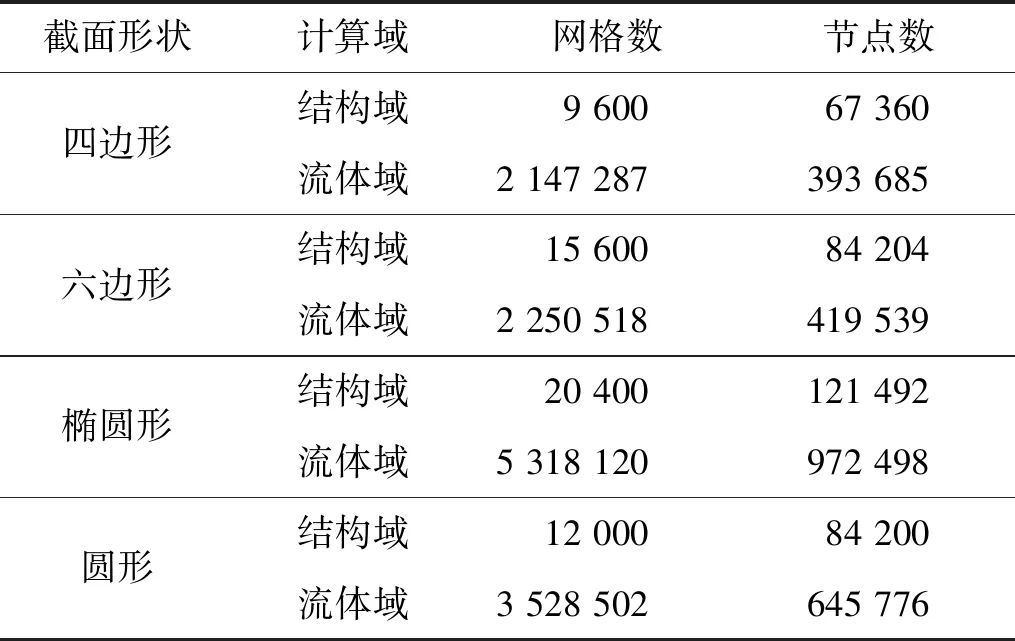
表1 網格數和節點數Tab.1 Number of grids and nodes

1.5 數據處理

管束在振動條件下面均傳熱系數的表達式為

h=q/ΔT

(7)

其中，

(8)

式中：q為壁面熱流密度；ΔT為對數平均溫差；Tin和Tout分別為殼程進出口流體的平均溫度；Twall為壁面溫度。

此外，為分析換熱器內所有管束的平均傳熱性能，定義平均傳熱系數為

(9)

式中：i為管束編號；n為管束數目；hi為管束i的面均傳熱系數。

1.6 結果驗證

文獻[15]研究了螺旋管束殼程振動強化傳熱特性，所用螺旋管束與本文螺旋彈性管束的結構、材料、流體介質均一致。為驗證本文計算結果的有效性，基于Jamshidi等建立的單螺旋彈性管束計算模型，采用本文粗算加精算的計算方法和網格劃分方法，對振動條件下的努塞爾數(Nu)進行了計算，并與試驗結果進行了對比，如圖5所示。

圖5 模擬結果與試驗結果的對比Fig.5 Comparison between simulation results and experimental data

從圖5可以看出，不同雷諾數Re條件下模擬結果與試驗結果的差距不大，最大相對誤差僅為3.05%。這說明，本文粗算加精算的計算方法和網格劃分方法是合理的且有效的。

2 結果與討論

2.1 振動響應分析

圖6所示為基于管束不同截面形狀的速度矢量圖。圖示截面為y-z面，vin=0.1 m/s。

從圖6可以看出：

(1) 流體進入換熱器后，首先沖擊殼程入口附近管束，而后沖擊換熱器內壁，改變流動方向后近似螺旋向左推進，最后從殼程出口流出。

(2) 不同截面形狀管束的速度分布不同，流體域上側流動更加強烈，且由于管束繞流作用，在流場內產生大量回流及渦流。

(3) 局部放大圖顯示，殼程流體主要以軸流方式沖刷管束，同時也會在其尾流區域產生一定的螺旋流。

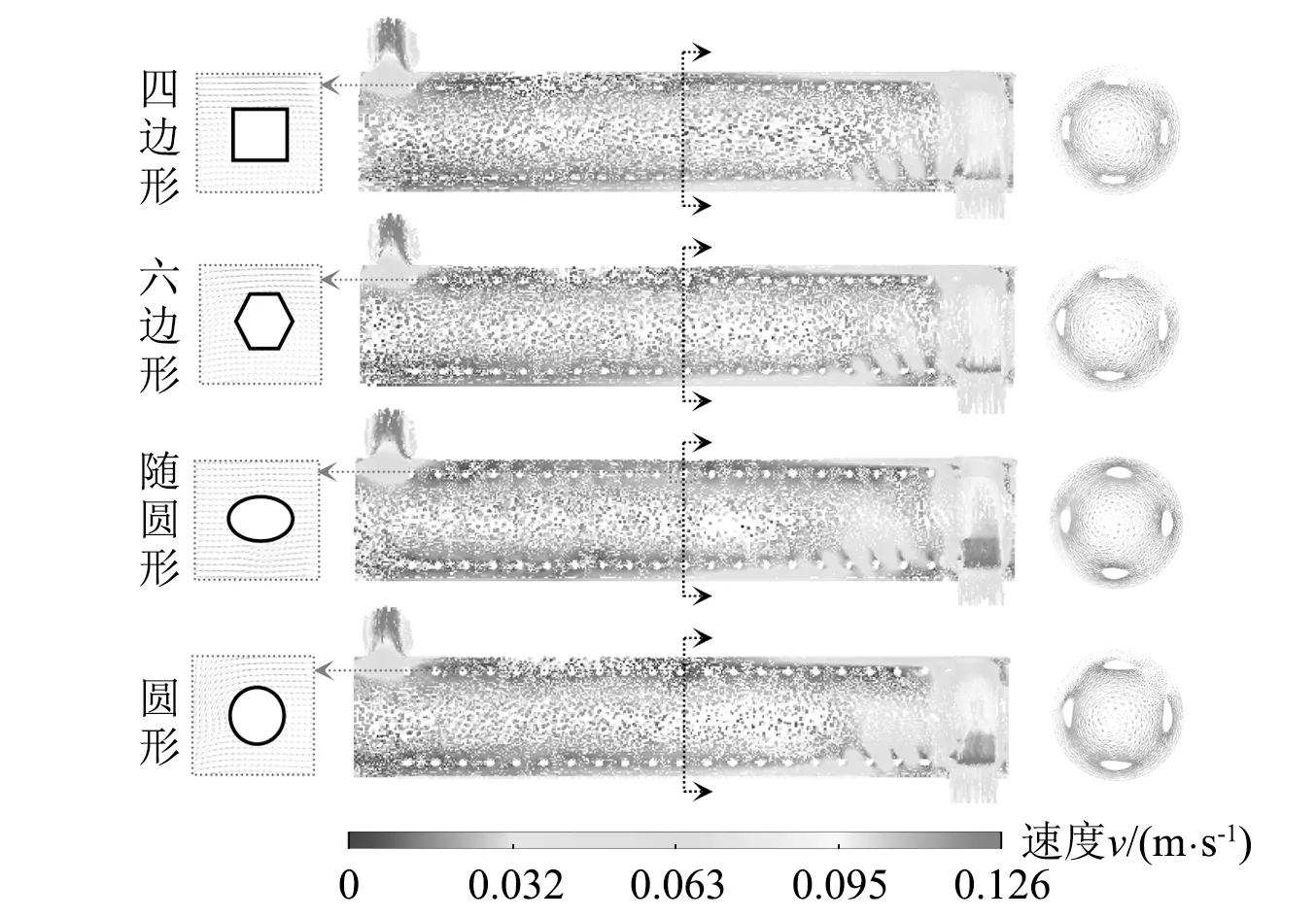
圖6 基于不同截面形狀的速度矢量圖Fig.6 Velocity vector diagram based on different section shapes

為了對殼程流體誘導下螺旋彈性管束的振動響應進行分析，在每根管束的中心位置設置監測點。表2所示為不同截面形狀下監測點的振幅(A)和頻率(f)情況。其中，vin=0.1 m/s。

表2 不同條件下監測點的頻率和幅值Tab.2 Frequency and amplitude of monitoring points under different conditions

從表2可以得出：

(1) 對于四邊形和六邊形截面，管1、管4的振動較劇烈，且振動頻率略低；對于橢圓形和圓形截面，管2、管3的振動較劇烈，且振動頻率略低。

(2) 對于管1、管4而言，振幅由高到低，截面形狀依次為：四邊形、六邊形、橢圓形、圓形；對于管2、管3而言，振幅由高到低，截面形狀依次為：橢圓形、四邊形、圓形、六邊形。

綜上，由于殼程流場的作用，不同截面形狀的螺旋彈性管束在換熱器內不同安裝位置的振動響應有明顯的不同。對于管1、管4而言，截面為四邊形的螺旋彈性管束的振動最劇烈，對于管2、管3而言，截面為橢圓形的螺旋彈性管束的振動最劇烈。

2.2 不同截面形狀的傳熱性能

圖7所示為基于管束不同截面形狀的溫度場分布云圖。圖示截面為y-z面，vin=0.1 m/s。

從圖7可以看到：

(1) 由于螺旋彈性管束的振動傳熱作用，殼程入口的低溫流體逐漸被加熱后從殼程出口流出。

圖7 基于不同截面形狀的溫度場分布云圖Fig.7 Temperature distribution nephogram based on different section shapes

(2) 截面為四邊形、六邊形和圓形的管束在頂部靠近殼程出口處存在高溫流體集中區域。

(3) 截面為橢圓形的管束溫度場的過度更加均勻，且在頂部的高溫流體集中區域很小。

圖8所示為振動條件下基于管束不同截面形狀的單根管束傳熱系數(hi)分布情況。其中，vin=0.1 m/s。

圖8 基于不同截面形狀的振動傳熱系數Fig.8 Vibration heat transfer coefficients based on different section shapes

從圖8可以看到：

(1) 相同截面形狀條件下，管1在振動條件下的傳熱系數均最高，說明管1的傳熱性能最佳。

(2) 不同截面形狀條件下管束的傳熱性能不同，截面為橢圓形的管束在振動條件下的傳熱系數最高、圓形次之、四邊形最低，說明管束截面形狀為橢圓時的傳熱性能最佳。

為了進一步分析螺旋彈性管束的振動強化傳熱性能，基于不同的截面形狀，計算了管束在不振動條件下的平均傳熱系數(ha)，并與振動條件下的平均傳熱系數進行了對比，如圖9所示。其中，vin=0.1 m/s。

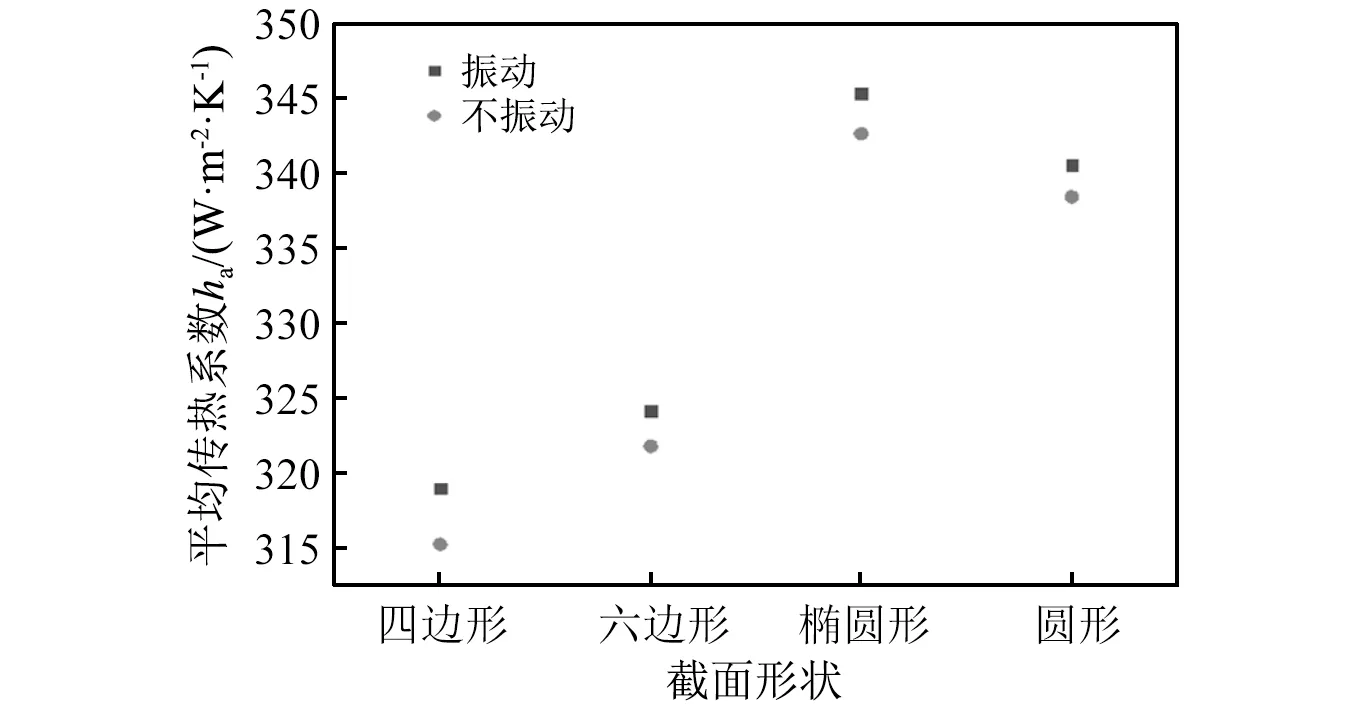
圖9 振動與不振動條件下不同截面形狀管束的平均傳熱系數Fig.9 Average heat transfer coefficients of tube bundle with different cross-sections under vibration and non-vibration conditions

從圖9可以看到：

(1) 振動條件下下管束的平均傳熱系數均高于不振動條件下的平均傳熱系數，說明流體誘導管束的振動實現了強化傳熱。

(2) 振動和不振動條件下截面為橢圓形的管束的平均傳熱系數均為最高，進一步說明管束截面形狀為橢圓時的傳熱性能最佳。

結合前面對振動響應的分析，對于管1、管4，截面為四邊形的螺旋彈性管束的振動最劇烈，但截面為橢圓形管束的傳熱性能最佳；對于管2、管3，截面為橢圓形的螺旋彈性管束的振動最劇烈，且截面為橢圓形管束的傳熱性能最佳。這說明，振動能夠實現強化傳熱，但振動劇烈的管束其傳熱性能并不一定是最佳，這種結論區別于Duan等、Ji等(2021年、2018年)的研究結論。因此在進行螺旋彈性管束換熱器設計時，并不是要一味追求高強度的振動，還要綜合考慮螺旋彈性管束的安裝位置和截面形狀。

2.3 不同入口流速的傳熱性能

圖10所示為振動條件下基于不同殼程入口流速的管束平均傳熱系數(ha)的分布情況。

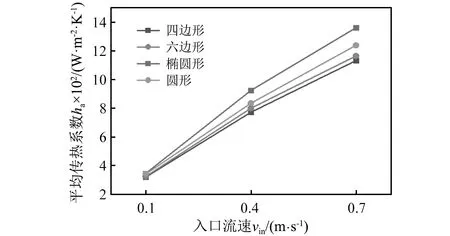
圖10 不同入口流速條件下不同截面形狀管束的平均傳熱系數Fig.10 Average heat transfer coefficients with different cross-sections under different inlet flow rates

從圖10可以看到：

(1) 不同截面形狀管束的平均傳熱系數均隨流速的增加而增加，當流速0.1 m/s從增加到0.7 m/s時，截面為四邊形、六邊形、橢圓形和圓形的平均傳熱系數分別提高了254.9%，259.2%，294.3%和263.8%，說明截面為橢圓形的管束的傳熱性能受流速的影響最大。

(2) 同一流速條件下，截面為橢圓形的管束的平均傳熱系數均為最高。當vin=0.7 m/s時，其相對于截面為圓形、六邊形和四邊形管束的平均傳熱系數分別提高了20.3%，17.0%，9.9%。說明不同流速條件下橢圓形管束的傳熱性能始終為最優。

為了進一步分析螺旋彈性管束的振動強化傳熱性能，基于不同的殼程入口流速，計算了截面為橢圓形的管束在不振動條件下的平均傳熱系數(ha)，并與振動條件下的平均傳熱系數進行了對比，如圖11所示。

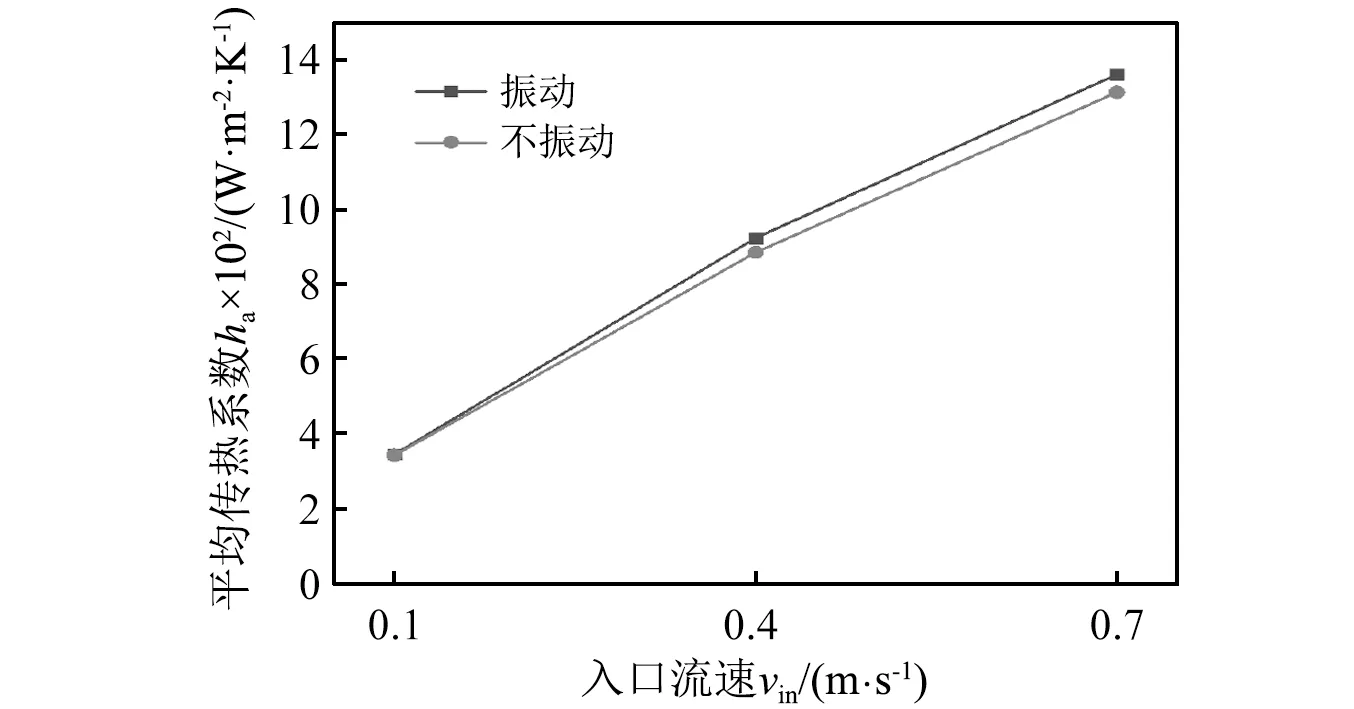
圖11 橢圓形管束振動與不振動時的平均傳熱系數Fig.11 Average heat transfer coefficients of tube bundle with elliptical cross section under vibration and non-vibration conditions

從圖11可以看到：

(1) 不同流速條件下，截面為橢圓形的管束在振動條件下的平均傳熱系數分別提高了0.8%，4.2%和3.5%，振動條件下的平均傳熱系數均高于不振動條件下的平均傳熱系數。

(2) 當流速0.1 m/s從增加到0.7 m/s時，不振動條件下的平均傳熱系數增加了283.4%，振動條件下的平均傳熱系數增加了294.3%，說明管束在振動條件下傳熱性能受流速的影響更加明顯。

(3) 結合前面的分析(見圖10)，與振動強化傳熱相比，管束截面形狀的改變對管束的傳熱系數影響更大。

2.4 截面圓周局部傳熱性能

為了分析管束在截面圓周上的局部傳熱性能，基于圖2所示的四個截面位置Ⅰ、Ⅱ、Ⅲ、Ⅳ，分析了不同截面形狀條件下管束截面圓周的局部傳熱性能，如圖12所示。其中，vin=0.7 m/s。

圖12 不同條件下的局部傳熱系數Fig.12 Local heat transfer coefficients under different conditions

從圖12可以看到：

(1) 同一截面位置處，截面形狀為橢圓形的管束圓周上的局部傳熱系數均為最大，說明截面為橢圓形的管束局部傳熱性能最優。

(2) 不同截面位置處，基于相同截面形狀的圓周上的局部傳熱系數大小不一，這是由于不同截面處管束周圍流體的流動方向和大小不同所致。

(3) 總體來看，截面圓周270°(或90°)處局部傳熱系數為最大，180°處局部傳熱系數為最小。這是由于殼程流體繞流管束后引起的低壓及回流現象所致。

3 結 論

為探究截面形狀對螺旋彈性管束傳熱性能的影響，基于四種截面形狀(四邊形、六邊形、橢圓形和圓形)，采用雙向FSC計算，對單層四螺旋彈性管束在不同入口速度條件下的振動和傳熱特性進行了研究。主要結論如下：

(1) 由于螺旋彈性管束的繞流作用，在換熱器殼程流場內產生大量回流及渦流，致使不同截面形狀的螺旋彈性管束在換熱器內不同安裝位置的振動響應有明顯的不同。

(2) 不同流速條件下，截面為橢圓形的螺旋彈性管束在振動和不振動條件下的傳熱系數最高，說明管束截面形狀為橢圓時的傳熱性能最佳。

(3) 振動能夠實現強化傳熱，但振動劇烈的管束其傳熱性能并不一定最佳，在進行螺旋彈性管束換熱器設計時，并不是要一味追求高強度的振動，還要綜合考慮螺旋彈性管束的安裝位置和截面形狀。

(4) 同一截面位置處，截面形狀為橢圓形的螺旋彈性管束截面圓周均具有最大的局部傳熱系數。由于殼程流體繞流管束引起的低壓及回流現象，截面圓周270°(或90°)處的局部傳熱系數為最大，180°處的局部傳熱系數為最小。