潛水一維非穩定流方程的數值求解與工程應用

李 茹，魯海峰

(安徽理工大學 地球與環境學院，安徽 淮南 232001)

0 引言

研究潛水非穩定運動規律對于工程建設、地下水動態預報都有著重要的意義。潛水一維非穩定流方程在基坑降水水位、區域地下水流水位、溝渠流水位等預測預報方面有著廣泛應用。目前眾多學者針對潛水一維非穩定流方程的求解問題開展了大量的研究，如任紅蕾等[1]建立了含階梯函數型源匯項的溝渠附近潛水非穩定滲流模型，應用Laplace變換性質，求出了模型解析解，并利用數值法驗證了解析解的可靠性；秦志忠[2]建立基坑降水有限元模型，探究了基坑周邊水位降深變化曲線；王照亮、郭昆等[3-4]通過建立數學模型以及水文地質概念模型，利用FEFLOW數值模擬軟件研究了地下水流場、分層的均衡性、潛水埋深、潛水水位；徐進、劉能勝等[5-6]基于Neuman模型，利用伽遼金法與正交解析函數族推導了解耦形式的加權余量方程式，并在編制Fortran計算程序實現數值求解的基礎上，提出了潛水非穩定流的半解析數值求解格式；張年學等[7]提出了一種新的解析方法，對隔水層正傾和反傾兩種情況，選取適當坐標，將含水層分為上下兩部分，根據層間越流流量變化率相等原理與質量守恒定律，導出全微分方程，獲得了解析解；夏強等[8]針對河渠間潛水的一維非穩定運動，考慮了補給強度的時變性，根據Boussinesq方程的第一線性化方法，應用Duhamel原理得到了方程的解析解。

上述研究成果在一定程度上對于潛水一維非穩定流方程的求解及應用起到了積極的指導作用，但聯合采用解析解和數值解系統探討此類水流方程的求解精度以便更好地指導實際工程的研究成果則較少。為此，本文采用分離變量法與有限差分法，以一類邊界條件為例，系統探討潛水一維非穩定流方程的求解方法與精度變化規律，擬為工程實踐提供理論指導。

1 潛水一維非穩定流方程模型及求解

1.1 方程建立

在描述河間區域地下水流、排水溝渠等地下水頭隨時間變化的非穩定滲流場時，一般可建立潛水一維非穩定流方程，在初始條件下地下水頭有一個二次函數形式的降深時，潛水一維非穩定流方程模型初始降深曲線如圖1所示。

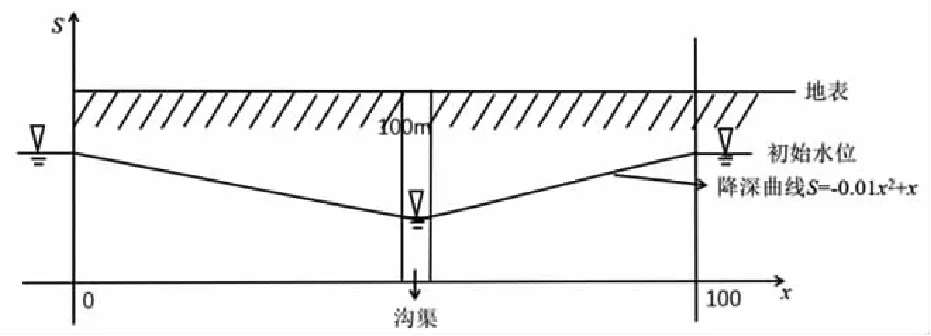
圖1 一維非穩定流方程模型初始降深曲線

在一類邊界條件[9]下，潛水一維非穩定流的偏微分方程及其定解條件為：

(1)

式中，T為含水層導水系數(m2/d)，μ為潛水含水層給水度，S為水位降深(m)，x為含水層寬度方向坐標(m)，t為時間(d)，L為研究潛水含水層水頭降深變化的范圍長度。

1.2 方程求解

偏微分方程的求解方法一般有解析法和數值法等[10]，解析法通常采用分離變量法，數值法通常采用有限差分法。本文同時采用這兩種方法求解，對數值解的精度進行系統討論和分析，并將顯式差分法和隱式差分法不同網格密度的數值解與解析解進行對比。

1.2.1 解析法

由式(1)可知，該方程為二階偏微分方程，邊界條件為一類邊界條件，且此邊界條件為齊次[11]。所以這里采用分離變量法來求解，具體求解過程如下。

將二階齊次偏微分方程轉化為兩個常微分方程。假設給定方程的解具有以下形式：

S(x，t)=X(x)T(t)，

(2)

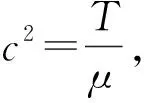
(3)

由式(1)中的邊界條件可得：

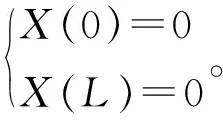
(4)

將方程(3)分為兩個部分進行求解，結合給出的邊界條件，根據λ取值的正負，最后推出給定問題的特征值是：

(5)

對應的特征函數分別具有以下形式：

(6)

這里Cn是任意常數。

由式(6)得到的方程通解及式(1)中的初始邊界條件S(x，0)=-0.01x2+x，可得：

(7)

由此解析解方程可表示為：

(8)

取L=100 m，T=51 m2/d，μ=0.3，根據式(8)，運用Matlab軟件求解出降深S隨時間t變化的規律曲線，如圖2所示。

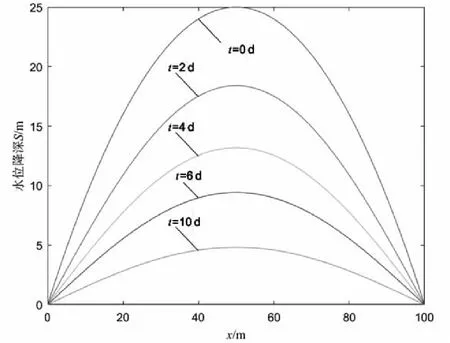
圖2 解析法求出的降深隨時間變化的規律曲線

由圖2可以看出，在一定時間內，降深S在含水層區間范圍內呈規律性變化，降深在邊界處的水位不變，在區間中部最大。由于含水層區間兩側有水源的徑流，可補給該潛水含水層，因此降深隨時間的增大而減小，經過第10 d后，最大降深已經小于5 m，水位恢復較快。

1.2.2 數值法

解析法一般只能針對方程以及邊界較為簡單的情形求解，隨著計算機技術的飛速發展，數值法已成為偏微分方程的主要求解方法。本文分別采用顯式差分和隱式差分兩種方法進行數值法求解[12]，并將求解結果與解析解進行對比，進而討論求解精度。

1.2.2.1 顯式差分法

將式(1)中的x方向分成n個節點，共有(n-1)個間隔；將t分成m個節點，共有(m-1)個間隔；將偏微分方程寫成差分方程，x方向步長為h，t方向步長為k。可得到如下方程：

(9)

由式(1)和方程(9)聯立可得：

(10)

進一步對式(10)中的步長h和k進行變換，得：

(11)

Si，j+1-Si，j=γ(Si+1，j+Si-1，j-2Si，j)。

(12)

將式(12)變換，得：

Si，j+1=γSi+1，j+(1-2γ)Si，j+γSi-1，j。

(13)

式(13)為該模型的顯式差分方程式。運用Matlab軟件求解出降深S隨時間t變化的規律曲線，如圖3所示。

圖3 顯式差分法求出的降深隨時間變化的規律曲線

由于顯式差分法剖分的網格數會對計算結果產生較大的影響[13]，為探討網格數對精度的影響規律，本文分別設置三種不同密度的網格。低密度網格時間t的步長為0.2 d，x的步長為10 m，結果為圖3中的虛線部分，從中可以看出，在時間開始時刻即t=0 d時，函數圖像曲線較為曲折，與解析法模擬出的結果相差較大；在t=6 d時函數圖像曲線較為光滑，可近似擬合解析法計算結果。中密度網格時間t的步長為0.02 d，x的步長為1 m，中密度網格顯式差分圖像如圖4所示。由圖4可以看出，當方程中的參數γ≥0.5時，計算結果不收斂，無法給出方程的解，這是由顯式差分法的固有缺陷造成的[14]。高密度網格時間t的步長為0.002 d，x的步長為1 m，結果為圖3中的實線部分，從中可以看出，函數圖像曲線整體光滑，在x=0處的同一時刻，通過此方法模擬出的結果與解析法模擬出的結果基本吻合；在接近區間中點即x=50 m時，得到的結果準確度較低。

圖4 中密度網格下顯式差分法計算結果

1.2.2.2 隱式差分法

由于顯式差分法對網格剖分有著較高的要求，下面討論隱式差分法的求解過程。將式(1)寫為隱式差分格式，可得：

(14)

由式(1)和方程(14)聯立可得：

(15)

Si，j+1-Si，j=γ(Si+1，j+1+Si-1，j+1-2Si，j+1)。

(16)

將式(16)變換后為：

(1+2γ)Si，j+1-γSi+1，j+1-γSi-1，j+1=Si，j，

(17)

式中，i=2，3，…，n-1，共(n-2)個節點。由此可建立方程組為：

(18)

根據此方程可變換為以下矩陣形式：

(19)

根據式(19)，采用追趕法在Matlab軟件中進行求解，并給出降深S隨時間t變化的規律曲線，結果如圖5所示。

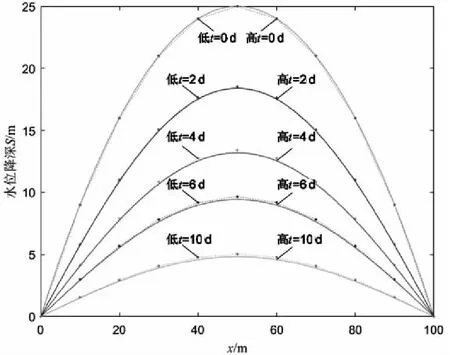
圖5 隱式差分法求出的降深隨時間變化的規律曲線

為探討網格數對精度的影響規律，同顯式差分法一樣采用三種不同密度的網格。低密度網格時間t的步長為0.2 d，x的步長為10 m，結果為圖5中的虛線部分，從中可以看出，在網格密度過低時，計算結果存在較大的偏差。高密度網格時間t的步長為0.002 d，x的步長為1 m，計算結果為圖5中的實線部分，從中可以看出，隨著網格數的增加，曲線更為光滑，計算結果更為精確，當t=0 d時，所呈現的曲線為初始降深，初始最大降深為25 m，隨著時間的增加，在地層同一點處的降深不斷減小。

為了與顯式差分法進行對比，同樣采用顯式差分法中的中密度網格，時間t的步長為0.02 d，x的步長為1 m，結果如圖6所示。對比圖6和圖4可以看出，隱式差分的網格剖分不受γ取值的限制，在不滿足γ<0.5時，計算結果依然收斂，由此顯示出隱式差分法的優越性。

圖6 中密度網格下隱式差分法計算結果

1.3 結果對照

為反映各種計算方法的精確度，選取其中一組數據進行誤差對比。這里選取時間為6 d時的數據，對照結果如表1所示。

表1 部分節點降深取值對照表 m

2 實例應用

下面對潛水一維非穩定流方程在一類邊界下的各種求解方法進行實例運用。某地鐵線路在建設施工過程中，在基坑開挖時遇到了潛水含水層，這將會對工程建設以及基坑開挖產生重大影響[15]。圖7為某地鐵線路建設過程中基坑開挖示意圖。基坑開挖寬度為20 m，深度為15 m，長度為100 m，可視為潛水一維非穩定滲流。根據巖土勘察結果，場地潛水含水層水位埋深為3 m，含水層厚度為17 m，巖性主要為粉砂，含水層滲透系數K=5.1 m/d。工程設計時采用井點抽水方式對基坑進行降水，為準確掌握抽水停止后水位恢復情況，采用潛水一維非穩定流方程進行求解。

2.1 建立模型

假設抽水一定時間后，地下水位的降深曲線滿足二次函數形式(如圖7所示)，以下將討論抽水停止后基坑水位恢復情況，其水位降深方程為：

(20)

其定解條件可描述為：

(21)

含水層滲透系數K=5.1 m/d，含水層厚度M=20 m，給水度μ=0.3，將潛水含水層線性化[16]，可得到含水層導水系數T=K(M/2)=51 m2/d。

圖7 某地鐵線路基坑開挖示意圖

2.2 求解方程

根據前面的研究結果，采用解析法和隱式差分法進行求解，圖8為隱式差分法和解析法模擬抽水停止后水位恢復的動態演變過程。

圖8 某地鐵線路基坑降深恢復曲線

通過圖8可知，地鐵工程的不同時間段對地下水位的影響程度不同。停止抽水時，該基坑地下含水層中部即x=50 m處的水頭降深最大，為25 m。隨著時間的變化，地下水位慢慢恢復，在停止抽水后第4 d水位恢復速率減慢，到第10 d水位基本恢復，直至最后地下水降落漏斗消失，水位恢復到初始狀態，且地下水環境趨于平穩。根據結果分析可知，基坑停止抽水1 d后基坑中部水位已上升到坑底。

3 結論

(1)對潛水一維非穩定流水位降深規律進行研究，建立降深隨時間變化的方程模型，借助分離變量法和有限差分法求解方程的解析解和數值解，對數值解剖分不同密度的網格，采用顯式差分法和隱式差分法進行求解，以此討論計算精度變化規律。

(2)顯式差分和隱式差分求解方法的模擬結果相差不大，在相同密度網格剖分下，顯式差分法較隱式差分法的求解精度要高，但顯式差分法存在網格約束條件，在實際應用時需注意網格剖分密度。

(3)實例應用表明，潛水一維非穩定流方程可很好地用于實際工程，為工程建設過程中地下水滲流計算提供理論基礎。