重載長行程機械臂設計及力學性能分析

程 燚，吳斌方，石 康

(湖北工業大學機械工程學院，湖北 武漢 430068)

侯保林等[1]利用Houboult法求解重載高速送料機械臂的運動方程，針對做大剛體運動的典型機械系統獲得具有普遍意義的運動規律。張莉[2]運用D-H參數法在靜力學和模態分析基礎上對重載冗余機械臂進行實操模擬和樣機實驗研究。武欣竹等[3]從伺服諧振和機械共振的角度對某桁架機械手的抖動現象進行分析，發現減速器輸出軸連接鍵結構強度差是造成橫梁振動的根本原因。畢厚煌等[4]設計出一種可實時調整碳棒電極高度的懸臂式起重機構，將絲杠機構柔性化以建立懸臂式起重機的剛柔耦合模型，對比剛體模型與剛柔耦合模型的仿真結果，獲得更加接近實際運行情況的數據，為整體結構進一步優化打下基礎。王相兵等[5]運用多柔體動力學理論，結合拉格朗日定理、虛功原理等，建立挖掘機機械臂柔性體模型，并對其進行仿真和數值求解，對比兩種不同操作結果驗證建模的正確性，同時，數值求解得到模態相關參數為結構的進一步優化提供參考。為了實現重載和長行程的生產需求，本文設計了一款全新的送料機械臂。

1 送料機械臂設計工作原理及應用

1.1 送料機械臂

由于棒料芯模較重，采用對稱的雙臂結構可有效增強機械臂承載能力。考慮到該棒料芯模兩端均有低精度的圓柱面，芯模長5～13 m不等，采用對稱聯合作業的機械臂設計，不僅可以根據芯模實際長度調整距離，還能保證芯模在運輸過程中的平穩性。此外，通過上部機械臂的左右運動將芯模在機床與機械臂間來回運輸，機械臂底座上安裝的軌道輪，可以實現在軌機械臂上的芯模長距離內外往復運輸。機械臂整體行程不得低于2600 mm，上部機械臂行程設計為2380 mm，才能滿足實際使用要求。送料機械臂主要由底座、伸縮系統及舉升系統組成(圖1)。

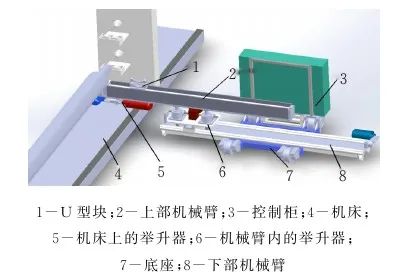
圖1 送料機械系統結構

1.2 機械臂橫梁構件

為了研究上部機械臂的固有頻率和振型，將其從裝配體中分離開來。上部機械臂主要包括兩端的絲桿支撐座、連接舉升機構的連接板、連接板兩側的加強筋和在導軌上滑動的滑塊等幾個部分組成(圖2)。該結構主要為鋼材焊接，在焊接后進行熱處理以消除應力，在對其進行力學模型仿真分析時，可忽略焊接應力的影響，建模過程將其視為一個整體進行分析。

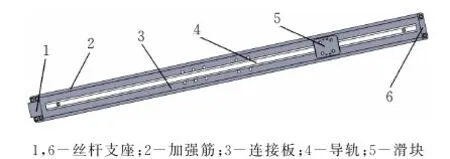
圖2 上部機械臂組成結構

送料機械臂主要結構參數如表1所示。

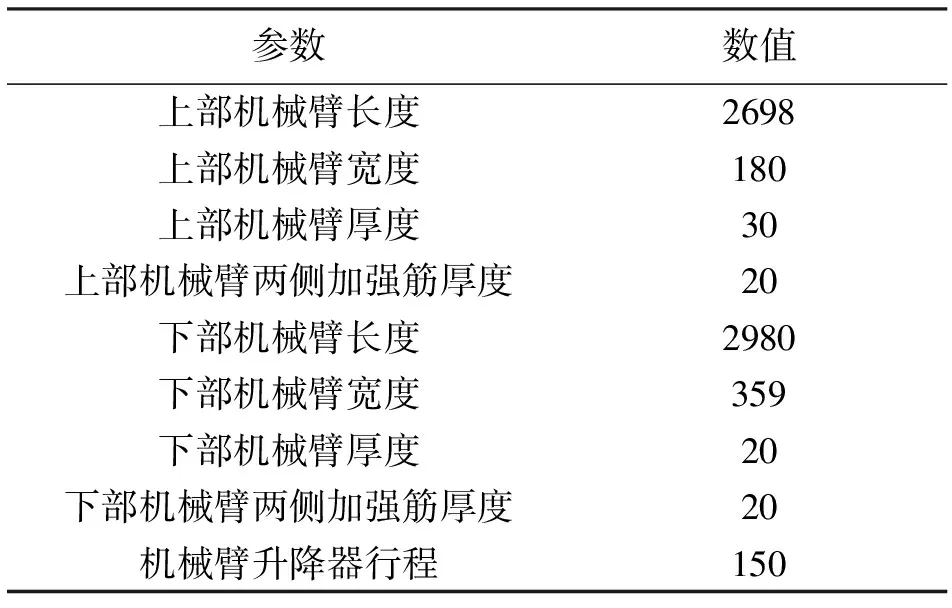
表1 機械臂的主要結構參數 mm

1.3 重載長行程機械臂

考慮到兩機床中心距長達4938 mm，運行軌道距兩側機床中心距分別為2410 mm和2528 mm，而生產中心的門寬僅為3 m，故該機械臂設計為上下伸縮式結構，以保證送料機械臂滿足同時運輸兩側芯模的要求。芯模為階梯軸類棒料芯模，芯模兩端為可運輸端，精度低；中間部位為纏繞成型區，精度極高。故考慮用U形塊來承接該棒料芯模，利用對稱機械臂進行聯合作業，將棒料芯模運送到指定地點。圖3、4為2～12 t棒料芯模的實物以及機床原始位置擺放。

圖3 棒料芯模實物

圖4 機床原始位置擺放

2 上部機械臂有限元分析

2.1 有限元模型的建立

在有限元分析之前，在不影響求解精度的條件下，對模型進行適當簡化處理，忽略主體結構中的凹槽、倒角、小孔等加工細節，避免產生應力集中的現象。在不影響機械臂橫梁強度的前提下，通過SolidWorks建立模型，并導入至ANSYS Workbench中，以滿足有限元分析的要求。得到簡化后的模型如圖5所示。

圖5 上部機械臂有限元分析模型

2.2 有限元模型網格劃分

上部機械臂總體呈現細長梁形狀，總長2698 mm，寬180 mm，高240 mm。由于上部機械臂主要用于承重，故最終選用的材料為結構鋼Q235以保證機械臂的抗彎和承載能力。上部機械臂主要使用板材焊接。為保證其網格劃分的質量，采用手動精細的網格劃分方法以增加求解結果精度。劃分成后，網格節點共計123311個，網格單元45614個。劃分完成后的模型如圖6所示。

1.2 儀器與設備 GC-MS-2010-plus型氣相色譜-質譜聯用儀，配有EI源，四級桿質量分析器；GC-MS Solution，日本島津公司；NIST05版質譜圖庫；DHG-9070A型電熱恒溫鼓風干燥箱，上海一恒科學儀器有限公司；57330U型手動SPME萃取手柄及65 μm聚二甲基硅氧烷-二乙烯基苯(PDMS/DVB)萃取探頭；20 mL精密螺紋口透明玻璃頂空進樣瓶，美國Supelco公司。

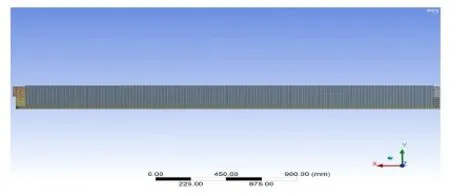
圖6 A級機械臂網格劃分

2.3 約束條件及邊界條件設置

定義上部機械臂中連接板方向為X方向，右端為正，沿著重力方向為Y方向，方向豎直向上，Z方向為絲桿支座方向，朝著操作者的方向為正。

對機械臂橫梁臂添加約束。由于上部機械臂與舉升機構相連接，故在上部機械臂上將位于下底面中心的10個孔位進行固定端約束。同時，當上部機械臂向左側伸出，運載型芯時，機械臂左側會擱置在機床上，防止型芯過重而導致機械臂發生側翻。故在機械臂左側設置固定端約束(圖7)。

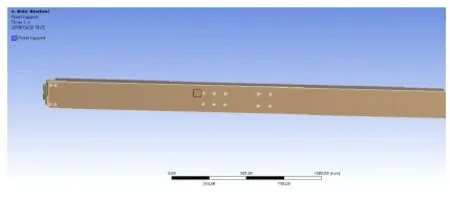
圖7 上部機械臂約束

由于該機械臂的主要外力來源于型芯的壓力以及自重，且型芯自重為12 t，為保證機械臂的正常使用，分析時將其設計為16 t；考慮到該機械臂采用一對對稱的機械臂進行聯合作業，對稱的機械臂同時運載型芯時，每個機械臂均受到8 t外加載荷以及自身重力。根據上部機械臂的結構，當滑塊位于上部機械臂右側中點時，為上部機械臂的危險狀態。對橫梁添加的外力和重力如圖8所示。

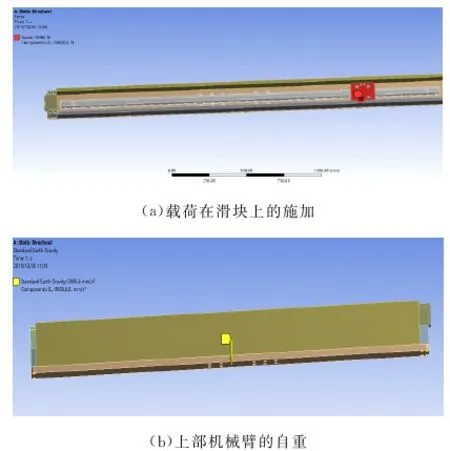
圖8 橫梁有限元分析載荷設置

2.4 有限元分析

對上部機械臂機械應力應變分析。上部機械臂在靜力作用下的最大應力應變如圖9所示，其中最大應變為0.090493 mm，最大應力為90.08 MPa，遠小于材料的許用應力應變值。故結構強度符合機械臂的使用要求，不會出現在應力作用下被破壞的情況。

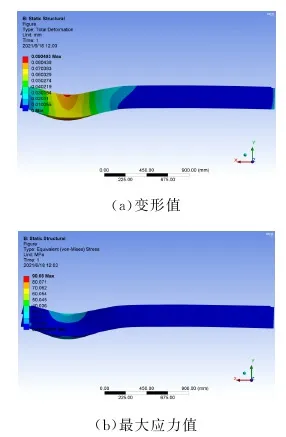
圖9 機械臂在靜力作用下的應力應變

對上部機械臂進行應力應變分析后，還需對其進行模態分析。圖10為上部機械臂前六階的振型云圖，可知其固有頻率在67.4671～312.61 Hz之間。

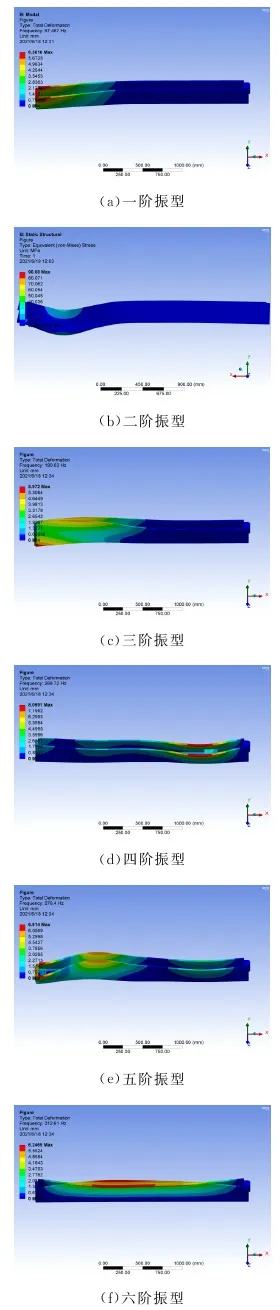
圖10 上部機械臂的的前六階振型云圖

可以看出第一階振形沿Z軸方向向內彎曲，第二階振形沿Y軸方向向上彎曲，一、二階振形最大變形量均發生在機械臂橫梁左側；第三階振形是沿Z軸方向彎曲扭轉，最大變形發生在機械臂橫梁左側；第四階振形是繞Y軸扭轉，橫梁右側變形較大；第五階振形為Y、Z軸方向的扭轉，最大變形量發生在機械臂橫梁左側；第六階振形是沿Z軸扭轉，最大變形出現在橫梁中心附近。

3 上部機械臂的諧響應分析

在工作過程中由于軌道不平穩，上部機械臂受到來自外加載荷產生的周期性作用力，當作用力的頻率與機械臂的固有頻率相同時，將發生共振。

諧響應分析的通用方程

(1)

力矩陣F和位移矩陣{u}是簡諧的，頻率為ω，用復數形式表示為：

{F(t)}={Fmaxeiφ}eiωt=({F1}+i{F2})eiωt

(2)

{u(t)}={umaxeiφ}eiωt=({u1}+i{u2})ei?t

(3)

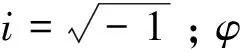
φ為位移函數的相位角；實部u1=umaxcosφ；虛部為u2=umaxsinφ。

諧響應分析的運動方程為：

(-ω2)[m]+iω[C]+

[K]({u1}+i{u2})=({F1}+{F2})

(4)

諧響應運動的求解方法主要有：完全法和模態疊加法，其中最快速的求解方法是模態疊加法。模態疊加法計算原理是將模態分析中的特征向量乘以因子，然后求和即可。

對上部機械臂進行諧響應分析時，在滑塊上施加一個激振力F，大小為68 600 N，在Workbench的Harmonic Response模塊中觀察上部機械臂在0～500 Hz頻率范圍內不同頻域下最大變形趨勢(圖11)。

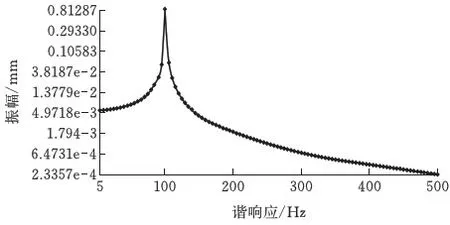
圖11 上部機械臂0～500 Hz諧響應

由圖11可知，在0～500 Hz的激振頻域范圍內，上部機械臂頻率在100 Hz處時，最大變形為0.1194 3mm，此時上部機械臂發生共振現象。

4 上部機械臂的模態試驗

通過模態分析結果可知，共振對上部機械臂及其兩側加強板影響最大，這將直接影響機械臂運輸過程中的平穩性，甚至對機械臂整個系統造成破壞。因此，通過諧響應分析判定機械臂的持續動力特性，確保整個機械臂能夠承受各種不同頻率的正弦載荷。

為驗證有限元模態分析結論的可靠性，對橫梁進行力錘單點敲擊，通過獲取其他點多點響應的測試方法進行了模態試驗(EXP)。試驗過程中，將軟繩連接懸梁并連接至模態分析傳感器，通過傳感器得到橫梁主要部位的振動位移信號。將采集到的激勵信號進行記錄后，通過分析軟件識別系統的模態參數。試驗所得結果(FEM)與有限元計算結果對比(FEW)如表2所示。

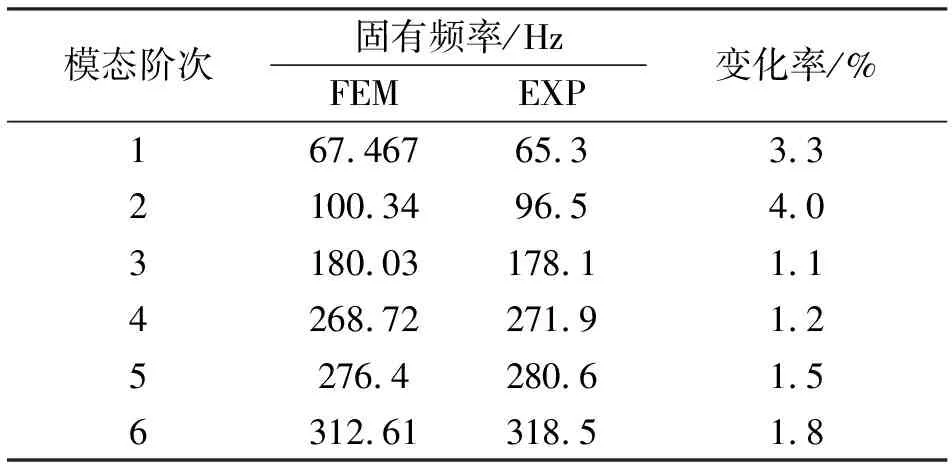
表2 橫梁模態試驗與有限元計算結果對比

由表2可知，模態試驗與模態分析計算結果相比較，最大誤差4.0%發生在第二階模態分析處。該試驗結果與有限元分析結果較為吻合，充分證明了采用有限元分析方法對自動上料機械臂進行模態分析時具有快速、可靠的優點。通過刺激頻率和計算頻率進行比較，避開固有頻率，可以有效防止系統共振帶來的影響，在一定程度上證明了本次試驗方法對于機械臂設計的參考價值。

5 結論

1)根據生產需求，設計了一款重載長行程送料機械臂，并且通過有限元軟件進行靜態分析，得出最大應變為0.090 493 mm，最大應力為90.08 MPa，遠小于材料的許用應力應變值，結構強度滿足2～12 t棒料2700 mm長行程輸送的設計要求。

2)通過六階模態分析云圖可以看出，上部機械臂的最大位移約為6 mm，位移距離較大，故需對各板材進行不同程度加厚，或者在合適的部位添加加強筋來保證機械臂的剛度。通過諧響應分析可以看出，當上部機械臂頻率在100 Hz時，最大變形為0.119 43 mm。

3)對該送料機械臂進行模態實驗研究，對比有限元分析結果，得出最大誤差為4.0%，發生在第二階模態分析處。該試驗結果與有限元分析結果較為吻合，為避免共振提供了數據支持，為解決類似問題提供很好的借鑒。