基于TPE-LSTM的區域超短期風電功率預測

查雯婷 閆利成 陳 波 李亞龍 楊 帆

1(中國礦業大學(北京)機電與信息工程學院 北京 100083)2(內蒙古電力科學研究院 內蒙古 呼和浩特 010020)

0 引 言

風能作為一種不確定性電源，隨著其在電力系統中的比例逐年升高，大規模集群入網的方式對系統調度帶來了巨大的挑戰[1-2]。同樣電力系統的不確定性也急劇增加，如何提高風電功率的預測精度成為該領域的研究熱點之一[3]。然而目前的研究對象多為單一風電場，鮮有對大區域的風電功率預測研究[4]。高精度的區域級超短期風電功率預測對風電并網、風電定價等方面有著重要的參考價值[5]。區域風電場和單一風電場的功率預測情況有所不同。單一風電場的研究數據可選用歷史功率數據、天氣預報(NWP)數據和風電場周圍的物理信息數據等。但區域預測時由于不同地區的差異性導致大多特征數據都難以適用，只能選用歷史功率數據作為研究對象，故預測難度也更高。因此能否從歷史數據中挖掘到有用信息成為提高區域風電功率預測精度的關鍵。

目前區域級風電功率預測的方法或模型還很少，文獻[6]通過氣象預測數據與歷史數據的相似程度，采用加權平均外推法得到區域功率預測值。文獻[7]通過預測基準風電場功率而映射出各子區域功率，通過疊加再得到區域的風電功率。文獻[8]采用統計升尺度方法獲取區域風電功率。這些方法存在的問題是模型相對簡單，而區域風電功率數據的規律性較差，傳統的統計學習和機器學習模型難以獲得較高的預測精度。隨著大數據技術的進步和并行計算能力的提升，深度學習技術取得重大突破，神經網絡在時序預測領域得到廣泛應用[9]。其中循環神經網絡(RNN)正是一種處理時序數據的神經網絡，LSTM是RNN的改進模型，可以解決RNN在使用中存在的問題，同時兼顧數據的時序性和相關性[10]，能充分反映時間序列數據中的長期歷史信息[11]。文獻[12]使用LSTM預測居民用電負荷，并論證了LSTM相較于傳統預測方法的優越性。文獻[13]使用LSTM預測PM2.5的變化情況，實驗結果表明該模型既可以較準確地預測變化趨勢，又可以響應波動變化。文獻[14]提出了一種基于LSTM的股票預測模型，并對損失函數做正則化處理，結果表明該模型可以獲得較高的擬合程度。LSTM在時序預測領域中的廣泛應用，也為區域風電功率預測提供了可能。

超參數是指在開始學習過程之前設置的參數集，它的選取將直接決定網絡模型的拓撲結構。LSTM模型在構建過程中同樣需要設置很多超參數。為了找到最合適的超參數組合，并盡量降低時間資源和計算資源的消耗。文獻[15]提出了一種貝葉斯優化算法的變型，名為TPE(Tree-structured Parzen Estimator)的調優理論。貝葉斯優化算法可以看成通過先驗分布使用啟發式手段的一種間接的尋優方法，與網格搜索遍歷參數空間和隨機搜索[16]利用隨機數去求函數近似的最優解明顯不同。貝葉斯優化在搜索過程中會參考之前的參數信息，不斷更新先驗分布，因此可以迭代更少的次數，但精度更高。

為了提高區域超短期風電功率預測精度，本文采用TPE算法對LSTM模型中比較重要的部分超參數自動尋優，借助歷史風電功率數據完成模型的訓練。此外為了減小預測過程中存在的誤差，加入誤差校正環節對預測結果完成校正。為驗證TPE-LSTM網絡的預測精度，加入實際的工程預測數據、BP網絡和RNN網絡與其比較。同時為了進一步證實TPE算法對模型超參數尋優的有效性，將參考模型中重要的超參數同樣采用TPE算法尋優。

1 算法原理與方法

1.1 長短期記憶網絡

LSTM相比RNN在內部結構上多了一種自環結構的記憶單元(Memory Cell)。這樣的設計雖然提高了模型的復雜度，但可以很好地解決RNN在使用過程中存在的梯度消失或梯度爆炸等問題，能夠深入挖掘在時間序列中蘊含的內在規律。LSTM基本單元模型如圖1所示。

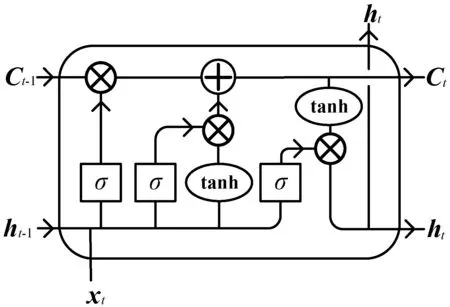
圖1 LSTM基本單元模型

記憶單元中的三個控制門：輸入門(Input Gate)、遺忘門(Forget Gate)和輸出門(Output Gate)。輸入門有條件地決定單元中存儲的信息，遺忘門確定計算單元歷史狀態信息的保留，輸出門控制信息輸出。Sigmoid激活函數可以將控制門的輸出映射到區間[0，1]內，當輸出值越接近0時，表示上一狀態的信息被舍棄得越多；當輸出值越接近1時，表示上一狀態的信息被保留得越多。LSTM的原理可以由式(1)-式(6)進行描述。

ft=Sigmoid(wf·[ht-1,xt]+bf)

(1)

it=Sigmoid(wi·[ht-1,xt]+bi)

(2)

ot=Sigmoid(wo·[ht-1,xt]+bo)

(5)

ht-1=ot×tanh(Ct)

(6)

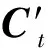
1.2 TPE算法原理

超參數尋優的目的是最大程度提高模型的性能或效果。優化過程如式(7)所示，其中配置空間X由所有需要優化的超參數組成，經過不斷調節模型的超參數，可以得到一組最優值x*。

x*=argminf(x)

(7)

式中:X是配置空間；f(x)是目標函數；x*是X中使得目標函數f(x)取得最小值的一組超參數。

貝葉斯優化是一種對模型超參數自動尋優的搜索方法，原理是基于目標函數在先前的評估結果建立以概率模型為依據的替代函數。與其他搜索算法相比，貝葉斯優化將搜索問題轉換成一個優化問題，并且在每次更新超參數時都會參考先前的觀測空間和優化結果。在文獻[15]中，Bergstra等提出一種貝葉斯優化的變體TPE算法來優化模型的超參數，其采用對p(x|y)和p(y)同時建模的方式代替只對p(y|x)建模。其中：p(y)代表解的分布情況；p(x|y)代表已知解的情況下，參數x的分布情況。此外引入優化標準EI用于引導搜索配置空間。p(x|y)計算如下：

式中：y′是已經定義好的閾值；l(x)表示觀測值x(i)的損失函數比y′小的密度估計值；g(x)表示觀測值x(i)的損失函數比y′大的密度組成。

為了防止在尋優過程中陷入局部最優，確保能夠遍歷所有有希望的配置區域。EI正好可以滿足這樣的要求，它可以理解為相對于閾值y′，新的超參數所對應的解所能提高的幅度。EI的定義如式(9)所示。

從式(10)可以看出，在最大化EI尋找更優的超參數過程中，EI應該逐步迭代到使g(x)/l(x)更小的值，即逼近最大概率的l(x)和最小概率的g(x)。

1.3 最小二乘多項式擬合校正

超參數尋優后的LSTM模型雖然具有強大的泛化能力，但是仍然存在一定的誤差。為了盡可能縮小模型預測誤差，采用最小二乘多項式以n階多項式擬合預測數據前的s個數據，擬合完成后得到擬合曲線并求取右端點外一個數據點的數值f(x′)。擬合過程使用的多項式如式(11)所示，具體的誤差校正過程如式(12)所示。

2 模型構建

為了實現風電功率預測，需要構建合適的神經網絡模型，以達到理想的預測效果。具體包括數據的修復及預處理、超參數優化、預測流程的確定和模型預測精度評價指標的選取。

2.1 數據的修復及預處理

由于獲取的數據中存在部分缺失，按照缺失數據時間間隔的長短分別采用線性插值和相似天填補的方法完成修復，并對其完成降噪以提高信噪比。

確保數據的完整性后，需要對數據進行歸一化處理。歸一化是一種無量綱的數據處理手段，把帶有單位的物理量線性映射到區間[0,1]內，處理成不含單位的相對值。此過程有利于降低運算量、加快收斂的速度和降低量值之間因為量綱和數量級的差異而帶來的影響。計算公式如式(13)所示。

式中:P′為歸一化后的風電功率值；Pt為當前的風電功率值；Pmax和Pmin為當組實驗數據中的風電功率數據的最大值和最小值。

2.2 超參數優化

使用TPE算法對LSTM網絡尋優時，首先應確定需要尋優的超參數和各超參數的取值范圍。本文模型主要優化的超參數包括輸入時間長度L、隱含層層數N和隱含層節點個數J等。輸入時間長度L表示訓練和預測過程中的歷史數據序列長度，其數值確定既需考慮歷史時序信息的完備利用，也需考慮預測模型的有效訓練。隱含層層數N即LSTM層的層數，它的選取需要衡量數據規模和訓練時間。隱含層節點個數J即LSTM層每一層中的神經元數量，可依據經驗公式得到取值范圍。經驗公式如式(14)所示。

式中：nh為隱含層的節點數；n為輸入層的節點個數；l為輸出層的節點個數：α為[1,10]之間的常數。

此外學習率R、迭代次數Epochs和批次大小Batch_size同樣很重要。其中，合適的學習率及批次大小設置有助于顯著提升深度學習模型迭代收斂速度與預測精度。

2.3 預測流程

考慮到風電功率受天氣和政治經濟等因素的影響，在超短期內具有一定的規律性。因此選取連續的一段數據作為數據集，并將其按照t∶v∶e的比例將數據劃分成訓練集、驗證集和測試集。訓練集和驗證集同為n∶l的多輸入、多輸出訓練模式，在完成訓練和驗證過程后保存最佳的模型，使用此模型實現對測試集的數據預測，完整的預測過程如圖2所示。

圖2 預測過程

網絡的輸出層采用LSTM網絡與全連接層連接的方式，并將此層的激活函數設為線性激活函數，目的是將具有強非線性特征的預測問題簡化成線性回歸問題。完整的模型預測流程如圖3所示。

圖3 模型預測流程

2.4 模型預測精度評價指標

以輸出層節點長度為單位統計每一次的預測結果，建立以均方根誤差(RMSE)、平均絕對百分誤差(MAPE)和合格率Q為評價指標的評價體系。RMSE和MAPE的計算如式(15)、式(16)所示，合格率的計算如式(17)、式(18)所示。

式中：Pp是風電功率預測值；Pr是風電功率真實值；n是目標預測數量；Sop為開機總容量。3個不同的評價指標均能反映模型的預測精度，其中：ρRMSE和ρMAPE越小表示預測誤差越小；Q則是越大表示預測誤差越小。

3 實驗與結果分析

根據上文建立的LSTM模型，選取北方某區域所有風力發電廠在2018年9月至2018年11月中旬共76天的歷史風電功率數據(時間分辨率為15分鐘)作為實驗數據。按照7 ∶3 ∶6的比例劃分成訓練集、驗證集和測試集。本文將測試集的比例提高是因為預測過程中用到的模型是已訓練好的模型，模型不需要重復訓練，提高測試集的比例以證明模型的泛化能力。模型的輸出尺度為4，將預測結果反歸一化后得到的數值即代表在未來1個小時的預測功率值。

3.1 LSTM網絡模型的確定

在超參數尋優過程中為了降低主觀判斷對模型預測精度的影響，在設置各超參數的選取范圍時盡可能做到廣泛、全面，這樣才能尋找到最佳的超參數組合。理論上3層的網絡已經可以逼近任何的非線性函數，從而將LSTM層數控制在4層以內。依據前文中需要確定的超參數，對超參數的取值范圍設置如表1所示。

表1 模型超參數取值范圍

經過TPE尋優得出的超參數配置如下。輸入節點個數為16；LSTM的層數為2，其中第一層LSTM網絡的節點個數為9，第二層LSTM網絡的節點個數為6，構成一個16- 9- 6- 4的四層神經網絡；激活函數為Sigmoid；Epochs為78；Batch_size為8；優化算法為Adam。

3.2 網絡模型對比實驗

為了驗證經TPE算法優化得到的LSTM模型可以更好地提升預測精度，進行對比實驗的BP和RNN同樣使用TPE算法尋優。由于受到數據數量級大小的影響，實驗結果的RMSE較大。模型預測精度如表2所示。

表2 模型預測精度對比

可以看出，TPE-LSTM模型與工程預測數據相比均方根誤差、平均絕對百分誤差分別只低了3.993、0.231百分點，合格率也高了2.015百分點，這說明TPE-LSTM已經超過了工程預測數據的預測精度，但是還比較有限。為進一步研究誤差校正對模型預測精度的影響。根據式(11)、式(12)對預測數據進行誤差校正。表3給出了TPE-BP、TPE-RNN和TPE-LSTM算法經過誤差校正之后的RMSE、MAPE和合格率。

表3 誤差校正后模型預測精度

為了更好地對比誤差校正對預測精度的影響，將TPE-BP、TPE-RNN和TPE-LSTM三種模型校正前后的數據結果進行對比，如圖4、圖5和圖6所示。

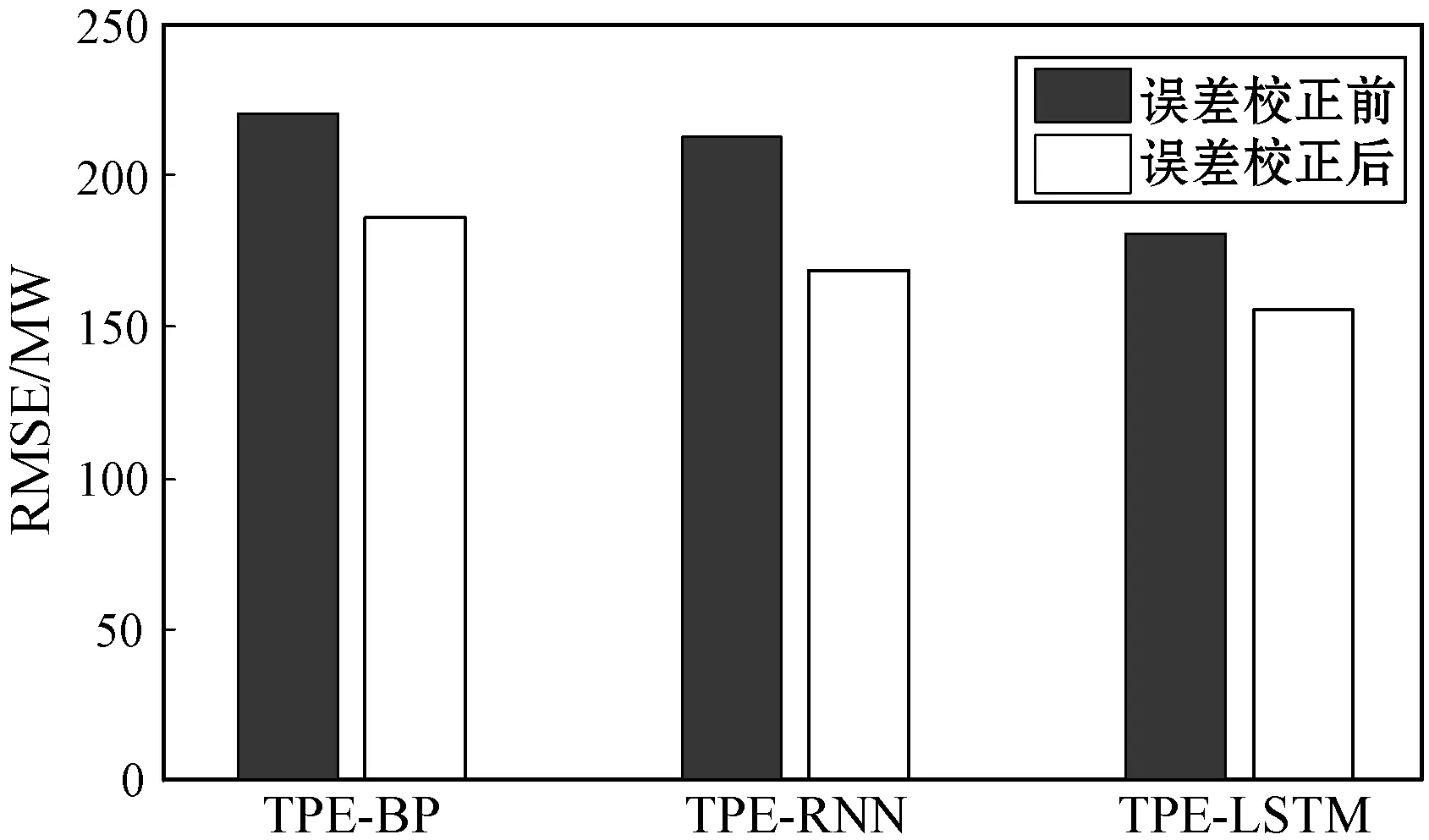
圖4 誤差校正前后RMSE對比

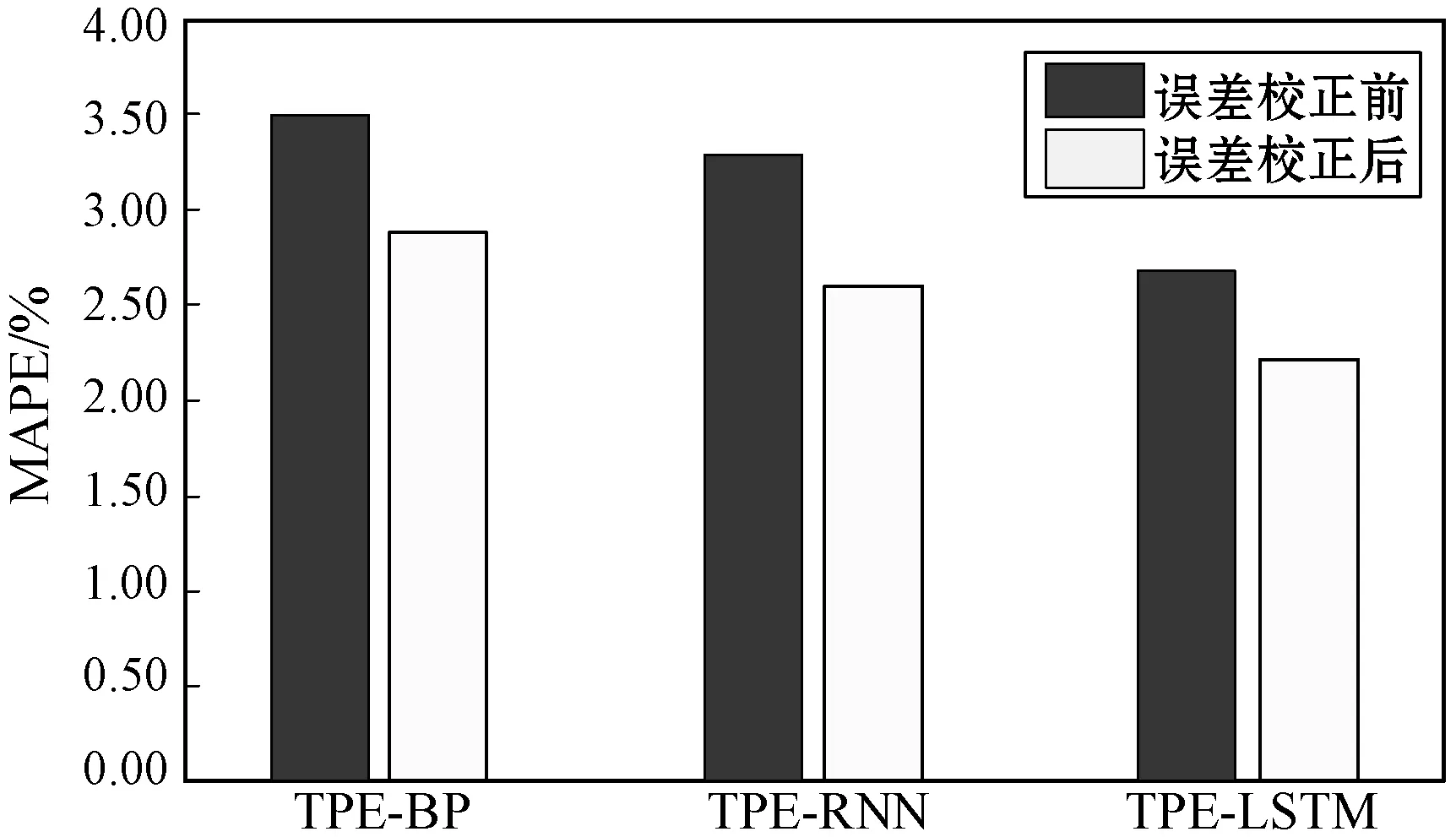
圖5 誤差校正前后MAPE對比

圖6 誤差校正前后合格率對比

可以看出誤差校正前后，三種模型的RMSE和MAPE均有不同程度的降低，合格率也均有不同程度的提升，其中TPE-LSTM的RMSE相較于誤差校正前降低了25.504，相較于工程預測數據較低了30.396；TPE-LSTM的RMSE相較于誤差校正前降低了0.497百分點，相較于工程預測數據較低了0.728百分點。從圖6中可以看出誤差校正前后，三種模型的合格率也均有不同程度的提升，其中TPE-LSTM的合格率相較于誤差校正前提高了2.579百分點，相較于工程預測數據提高了4.594百分點，此外TPE-BP和TPE-RNN的預測精度也同樣有較大的提升。實驗結果表明，誤差校正策略能夠有效降低算法預測誤差，提高算法的預測精度。

3.3 誤差校正有效性分析

為了驗證誤差校正可以有效減小模型在預測過程中存在的誤差，真正提升模型的預測精度。此節著重對比誤差校正后TPE-BP、TPE-RNN和TPE-LSTM三種模型的預測數據與工程預測數據之間的差異，對RMSE和MAPE以每4個數據為統計長度統計每次預測結果的RMSE和MAPE，統計后的RMSE分布情況如圖7所示，MAPE分布情況如圖8所示。

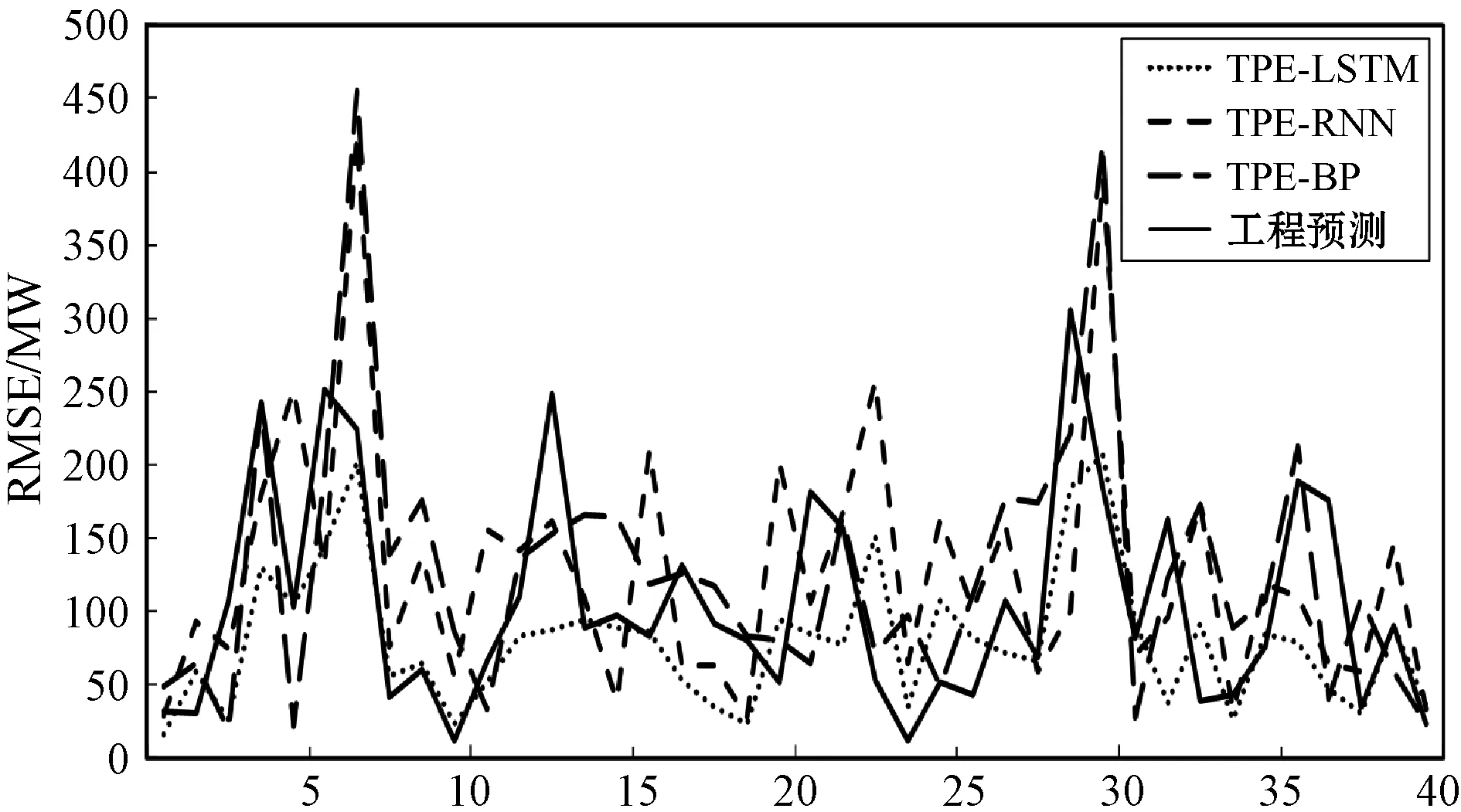
圖7 前40次預測結果的RMSE

圖7給出了誤差校正后TPE-LSTM、TPE-RNN、TPE-BP和工程預測數據在前40個預測點的RMSE對比。可以看出，TPE-LSTM的RMSE在四種模型中總體變化穩定且幅值也更小，這同時也證明TPE-LSTM模型的預測結果變化趨勢與真實數據更接近。

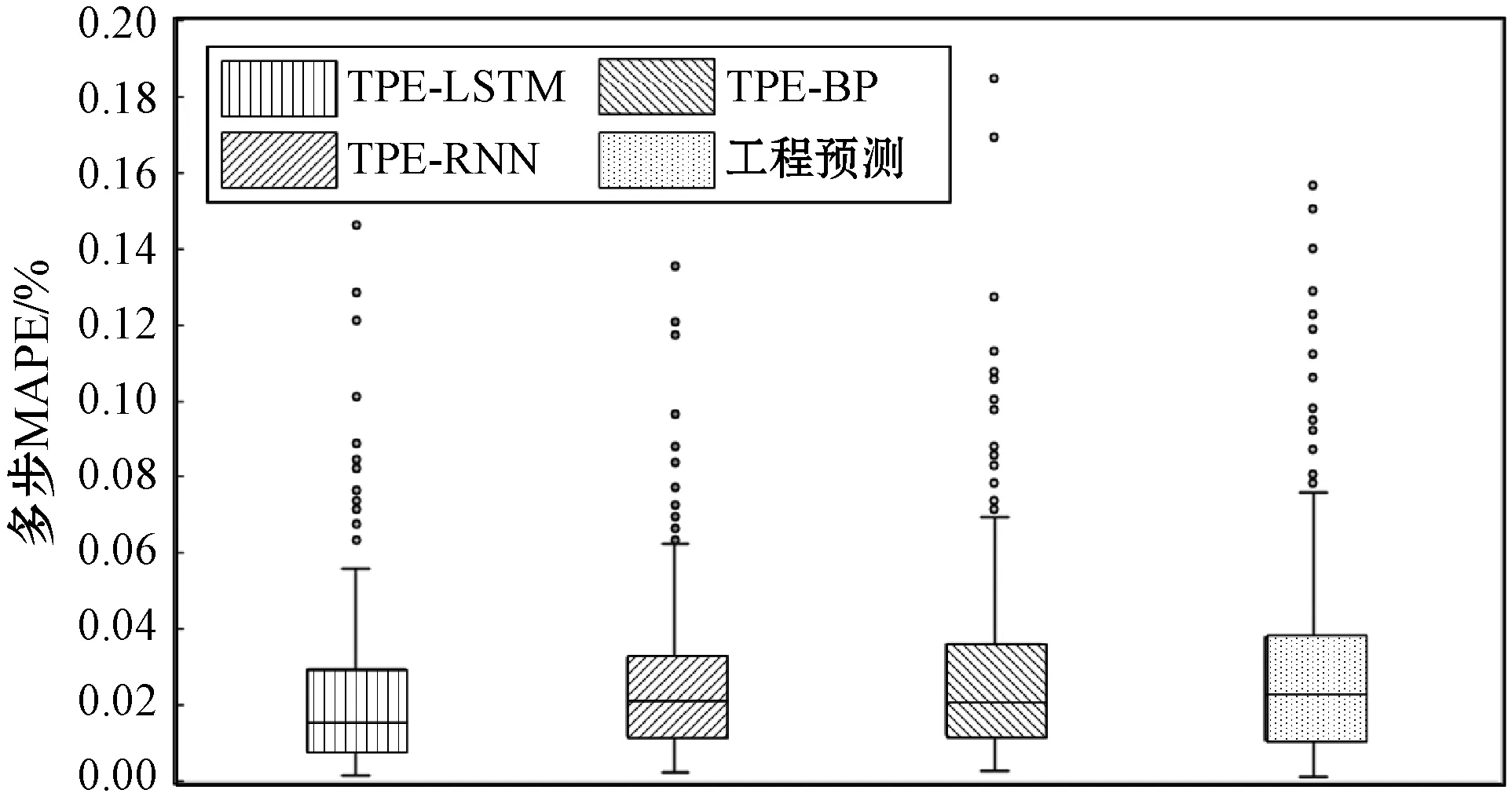
圖8 MAPE分布情況

從圖8中可以看出，誤差校正后TPE-LSTM數據的誤差分布情況更集中。其上邊緣、上四分位數、中位數和下四分位數也都是4種模型中最低的，并且其異常值也并不大，因此可以推斷出誤差校正后TPE-LSTM的MAPE應該也是最低的，表3中的數據也證明了這一點。因此相比之下，TPE-LSTM算法的預測效果具有更好的擬合效果和預測精度。

以上實驗結果表明，本文提出的TPE-LSTM模型預測結果精度更高，且預測結果波動小，誤差相對穩定，驗證了該算法的有效性。

4 結 語

利用歷史風電功率數據，提出一種基于TPE算法和LSTM的區域超短期風電功率預測方法，結果表明基于貝葉斯優化方法中的TPE算法可以解決神經網絡模型的超參數優化問題，具有迭代次數少、用時短等優勢。依據尋優后的超參數組合搭建的LSTM網絡模型具有較強的泛化能力，在區域超短期風電功率預測方面相較工程預測數據和其他模型具有較高的預測精度，是一種實際且可行的方法，在此領域中具有較好的應用前景。