基于徑向基函數的無網格法分析非均勻左手介質填充波導

翁倩茹 盧楚杰 潘思辰 謝恩德

1(成都工業學院智能制造學院 四川 成都 611730)2(廣東工業大學計算機學院 廣東 廣州 510006)

0 引 言

左手介質是一種介電常數ε和磁導率μ均為負數的新型人工介質，在這種介質中電場(E)、磁場(H)和坡印亭矢量(S)三者的方向呈現左手螺旋方向[1]。Pendry等[2]結合周期性排列的開口諧振環(Split ring resonators,SRRs)和金屬桿，首次物理實現了具有負折射的左手介質，自此之后，左手介質的理論和應用研究呈現爆發式的增長。其中一個重要的研究方向，就是用左手介質代替傳統介質應用于各種微波毫米波器件。近年的研究發現，在波導中填充非均勻左手介質會表現出奇異的傳播特性。例如在填充左手介質的矩形波導和圓波導中，都發現了低于截止頻率傳播的后向波傳播特性[3-7]。而這些奇異的電磁特性在小型化波導、后向波天線等毫米波集成電路器件中具有非常高的應用價值。

近年來，具有連續變化折射率的非均勻左手介質(又稱為梯度折射率左手介質)受到研究人員的廣泛關注。這種新型人工介質可以改變電磁波的傳播方向和傳播相位，在變換光學、調整電磁波束和電磁波隱身結構設計方面具有廣泛應用[8-10]。對于波導中左手介質非均勻性的精確求解，是各種毫米波和光波集成電路元器件設計和最優化的基礎。

除了一些特殊情況(例如均勻左手介質加載或內襯波導[3-4,6])，大多數非均勻左手介質填充波導結構不能求解析解。因此需要利用數值方法對于波導的特征值進行近似計算，常用的數值計算方法包括有限元法、時域有限差分法、矩量法和變分法等[11-13]。

然而，對于有限元法和時域有限差分法等方法，需要對研究區域進行網格的劃分，其未知數分布在整個研究區域中。并且非均勻介質區域需要高質量的網格劃分，其求解精度與網格劃分的質量密切相關，因而這些基于網格劃分的數值方法占用大量的計算、存儲和時間資源。

近幾年，基于徑向基函數(Radial basis functions,RBFs)的無網格方法受到了學界的廣泛關注[14-15],這項數值方法已經應用于各種電磁學問題如邊界問題[16]、反向散射問題[17]、波導分析[18]。這種方法的優點是不需要對研究區域進行網格生成，而是采用空間節點離散處理的方法。這種方法對于分析復雜結構，例如非均勻材料和不連續結構等，具有非常好的效果,因此對于非均勻左手介質結構的數值分析具有天然的優勢。

利用基于RBFs的無網格法分析非均勻左手介質時有兩個問題需要注意。(1) RBFs形狀參數的選取，采用唯一的形狀參數，會導致特征值的求解精度極其依賴于配置點的位置，進而造成特征值精度的降低。因此本文采用具有特定統計分布的高斯型隨機RBFs。(2) 采用點匹配技術分析非均勻介質時，會導致一個非對稱的特征問題，造成特征方程求解困難。因此本文采用變分法和無網格法結合的方法得到對稱的特征方程。

本文首次將基于RBFs的無網格法應用于非均勻左手介質填充波導特征值的計算中，并與解析法求得的精確結果和利用基于有限元法的電磁分析軟件HFSS得到的仿真結果進行對比，驗證了本文提出的無網格法在分析非均勻波導結構時的精確性和高效性。

1 數值方法及算法實現

1.1 場方程和基于徑向基函數的無網格法

非均勻左手介質填充矩形波導的橫截面面積A=a×b,Γ是矩形波導橫截面的邊界，該結構磁場H(x,y,z)的麥克斯韋方程組為：

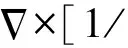
(1)

(4)

式中：ωpe和ωpm是等離子體頻率；Γe和Γm是阻尼系數；h(x)和g(x)是非均勻介質的剖面函數，描述非均勻介質的非均勻特性。

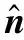
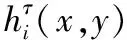
RBFs有各種類型，例如，高斯型、復二次函數型和反二次方程型，本方法采用文獻[20]中定義的高斯型RBFs：

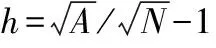
1.2 算法實現

利用基于RBFs的變分無網格法計算非均勻左手介質波導傳播特性的算法流程如圖1所示。本文算法由MATLAB編程實現。

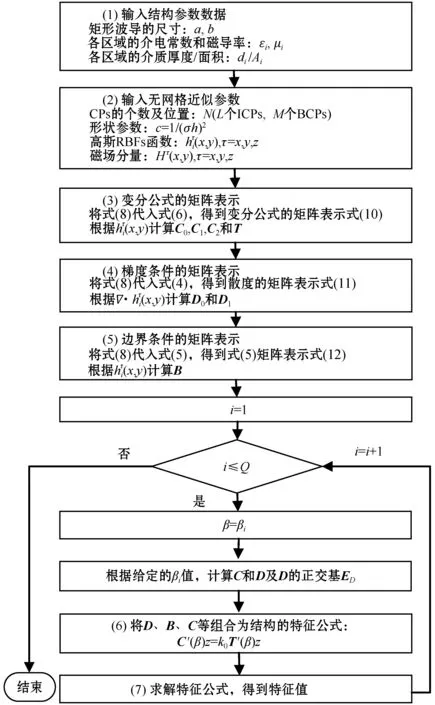
圖1 基于RBFs無網格法的算法流程

步驟(1) 輸入結構參數，包括波導的尺寸、波導中各非均勻區域的介電常數和磁導率，及各區域的厚度或面積。

步驟(2) 輸入無網格法的相關參數，包括CPs的定義、形狀參數的選取和RBFs函數的輸入，根據以上參數計算得到的磁場分量Hτ(x,y)。

步驟(3)-步驟(5) 將Hτ(x,y)代入式(6)、式(4)及式(5)的矩陣表示，如式(9)-式(13)所示。

Da=0

(10)

Ba=0

(11)

其中：

C=C0+βC1+β2C2

(12)

D=D0+βD1

(13)

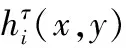
步驟(6)β-循環開始，計算β相關的矩陣C、D。之后，將式(9)-式(13)組合成特征方程，通過求解特征方程計算傳播常數β，Q為β值的計算次數。β-循環停止即表示所有的β值已經求解完畢，對應的傳播曲線繪制完成。

2 數值結果

本節利用基于徑向基函數的變分無網格法計算了三種典型的非均勻左手介質填充矩形波導結構的傳播特性。這三種結構在濾波器、耦合器、超材料特性的測量等方面都具有廣泛的應用，而且這三種結構是規則填充的情況，因此可以求得解析解。本文的計算結果分別與解析解和HFSS的仿真結果進行對比，通過對比可以得到以下兩點結論：

(1) 解析法得到的結果是特征值的精確解，因此與本文得到數值計算結果對比可以對無網格法的準確性和可行性進行分析。

(2) HFSS是目前最常用的基于有限元法的電磁數值分析工具，在相同精度要求下，對比無網格法和HFSS分析所需的時間，可以對無網格方法的效率進行分析。

這些結構作為微波電路的關鍵器件使用時，主要工作在主模式的狀態下，而非均勻矩形波導的主模式是縱剖面電模式(longitudinal-section electric mode,LSE mode),因此本文主要對非均勻波導結構的LSEn0模式進行分析。

2.1 單層左手介質加載矩形波導

本文研究的第一個例子如圖2所示，加載的左手介質將矩形波導分割為兩個區域，區域I為真空區域，其中：εr1=1，μr1=1；區域II中左手介質的介電常數、磁導率和厚度分別為εr2=-4，μr2=-1及d2/d1=1/3。LSEn0模式的傳播特性曲線如圖2所示，其中：黑色實線代表解析法的計算結果；黑色方塊代表無網格法的計算結果；黑色圓圈代表HFSS的仿真結果。該結構LSEn0模式的解析式為：

k2tan(k1d1)=-k1tan(k2d2)

(14)

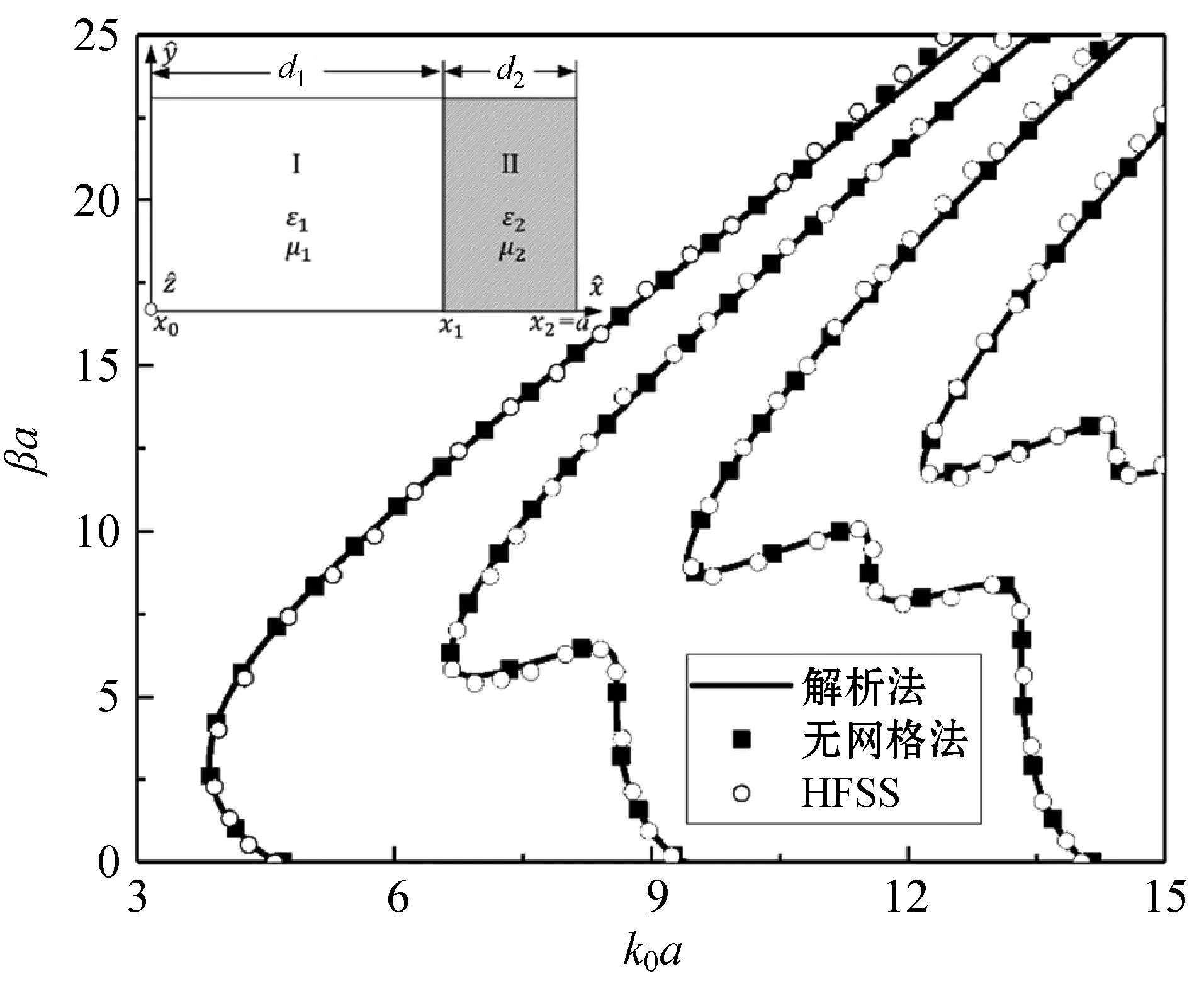
圖2 單層左手介質加載矩形波導的傳播特性曲線

利用式(14)可以求得該結構傳播特性曲線的精確解。對于無網格法，CPs的數量為N=100，其中ICPs的數量為70，BCPs的數量為30，計算96個特征值的代碼運行時間為6 s。作為對比，利用相同的工作站，HFSS仿真耗時接近3 min(180 s)。因此，相比于HFSS的分析時間，無網格法的數值分析效率非常高。圖2中，無網格法的數值解、解析法的精確解和HFSS的仿真結果具有非常好的一致性，因此說明無網格法的準確性。

通過圖2可以觀察到，一些頻段的群速度為負值(?k0/?β<0)，這與傳統波導中正群速度(?k0/?β>0)的傳播特性不同。在文獻[4]中，將這種負群速度的傳播特性稱為“左手傳播特性”。研究表明負群速度可能產生后向波傳播特性，因此如果在圖2所示的波導結構上適當開槽(slot)可以用作后向波輻射天線。

2.2 兩層左手介質對稱加載矩形波導

本文研究的第二個例子為如圖3所示的兩層左手介質對稱加載矩形波導，其中區域I和區域III為左手介質(εr1=εr3=-4，μr1=μr3=-1，d1=d3=0.15a)，區域II為真空區域(εr2=1，μr2=1)。LSEn0模式的傳播特性曲線如圖3所示，其中:黑色實線代表解析法的計算結果；黑色方塊代表無網格法的計算結果；黑色圓圈代表HFSS的仿真結果。該三層矩形波導結構的LSEn0模式的解析式為：

k2k3tank1d1+k1k3tank2d2+k1k2tank3d3-

利用式(15)可以求得傳播特性曲線的精確解。對于無網格法，CPs數量為N=326，其中ICPs的數量為282,BCPs的數量為44。計算87個特征值的代碼運行時間為8 s。作為對比，利用相同的工作站分析同樣的三層波導結構，HFSS仿真時長接近5 min(300 s)。圖3中，無網格法的數值解、解析法的精確解和HFSS的仿真結果具有非常好的一致性，說明無網格法分析該三層結構的準確性。

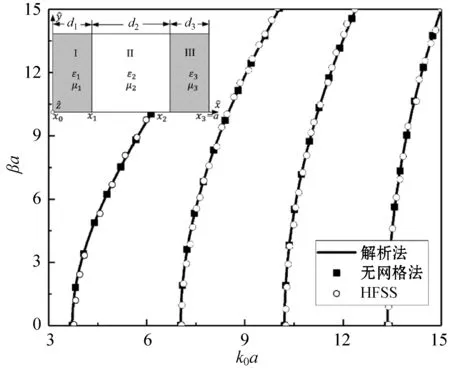
圖3 兩層相同的左手介質對稱加載矩形波導的傳播特性曲線

2.3 單層左手介質中心填充矩形波導

本文研究的第三個例子是對如圖4所示的單層左手介質中心填充矩形波導進行分析。填充的左手介質將矩形波導分割為3個區域，其中區域II為左手介質(εr2=-4，μr2=-1，d2=0.4a)，區域I和區域III為真空區域(εr1=εr3=1，μr1=μr3=1)。LSEn0模式的傳播特性曲線如圖4所示，其中：黑色實線代表解析法的計算結果；黑色方塊代表無網格法的計算結果；黑色圓圈代表HFSS的仿真結果。其中變分無網格法的CPs設定與2.2節中的設定相同，即CPs數量為N=326，ICPs的數量為282,BCPs的數量為44，而三層介質填充波導的特征方程依然為式(15)。計算79個特征值的代碼運行時間為6.5 s。作為對比，利用相同的工作站分析同樣的中心填充波導結構，HFSS仿真時長接近5 min(300 s)。圖4中，無網格法的數值解、解析法的精確解和HFSS的仿真結果具有非常好的一致性。在這種結構中在某些頻段中可以觀察到負群速度的“左手傳播特性”。

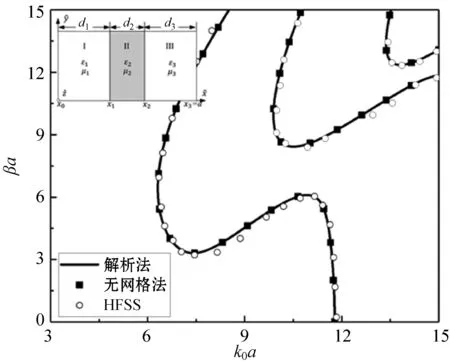
圖4 一層左手介質中心填充矩形波導的傳播特性曲線

3 結 語

本文將基于徑向基函數的變分無網格方法推廣到非均勻左手介質填充波導的數值計算中，這種方法的優勢在于無須對研究區域進行網格生成，大大節省了計算和存儲資源。特別是在包含非均勻介質、尖角及突變的復雜結構的分析中，無須對復雜區域進行額外的高質量高密度的網格劃分。因此該方法尤其適用于非均勻介質和不連續結構的數值分析。本文詳細地分析了三種具有代表性的非均勻左手介質波導結構，并且將無網格法得到的結果分別與精確的解析解和有限元法的仿真結果進行對比，說明無網格法在分析非均勻左手介質填充波導時具有精確度高和計算時間短的優點。分析結果得出，部分填充左手介質的矩形波導在某些頻段支持具有負群速度的后向波傳播模式(左手傳播模式)，為具有后向波輻射天線的設計提供了一種新結構。

在之后的研究中，計劃利用無網格法分析更加復雜的波導結構，例如近年提出的基片集成波導結構(SIW)和懸置微帶線結構等。此外，也計劃利用該方法分析更加多樣的新型介質。本文研究的左手介質是一種新型的人工電磁介質，而近年來各種各樣的人工電磁介質層出不窮，例如具有漸變折射率的人工電磁媒質、具有各種特性的光子晶體等，這些介質及含有這些介質波導的分析同樣需要準確的數值計算方法。因此，本文提出的無網格法為復雜波導和新型介質的數值分析提供一種高效而精確的方法。