基于人臉特征的可搜索加密方案

徐慧華 楊 雄

1(福建師范大學協和學院經濟與法學系 福建 福州 350117)2(福州大學至誠學院計算機工程系 福建 福州 350002)

0 引 言

一個典型的人臉識別系統首先采集人臉圖像，對其進行一些預處理后提取高維特征。在用戶注冊過程中，這些特征向量和用戶的身份標簽一起存儲于數據庫中。在用戶身份認證過程中使用該數據庫來驗證一個人所聲稱的身份，身份驗證過程即通過計算所聲稱身份的用戶人臉特征與該身份標簽在數據庫中所對應的人臉特征之間的相似度來完成。針對人臉識別系統最直接的攻擊點就是網絡傳輸的人臉特征和人臉特征數據庫。因此，若將人臉特征直接以明文形式進行網絡傳輸和存儲于數據庫中，會嚴重影響注冊用戶的隱私和認證系統的安全性。

為了提高人臉識別系統的安全性，可利用密碼系統對網絡傳輸和數據庫中存儲的人臉特征進行加密。然而，一般的加密方案還需要將人臉特征密文進行解密才能夠完成人臉匹配所需的基本算術運算。而同態加密方案支持對密文進行人臉匹配所需的算術運算[1]，能夠在加密域中實現人臉匹配，不需要對人臉特征密文解密，進一步提升了安全性。同態加密系統分為部分同態加密(Partially Homomorphic Encryption,PHE)[2]、somewhat同態加密[3]和全同態加密(Fully Homomorphic Encryption,FHE)[4]。雖然全同態加密在加密域支持無限的加法和乘法運算，比部分同態加密和somewhat同態加密在實際場景中更為通用，但隨之帶來的計算復雜度也更高。

目前流行的人臉匹配方法大多為基于深度神經網絡的方案，這些方案通過卷積神經網絡模型[5-7]從人臉圖像中提取出高維人臉特征后，計算人臉特征向量之間的歐氏距離，取最小距離所對應的人臉圖像的身份作為測試人臉圖像的身份。但在加密域中進行人臉匹配時，數百到上千維的人臉特征向量需要非常耗時的同態操作，導致其不適合在高維向量空間中進行運算[8]。

本文基于全同態加密方案CKKS[9]提出了一種高效的解決方案，探索了使用全同態加密的人臉特征進行人臉匹配的實用性。首先將典型的人臉匹配度量(歐氏距離)分解為一系列加法和乘法運算的組合；接著，利用中國剩余定理和批處理技術，通過旋轉加密向量，以logn個同態加法的代價實現n個同態加法，降低計算復雜度；最后，再利用近似最近鄰算法，以O(logN)的代價實現1 ∶N的人臉匹配，滿足實際應用場景的需求。

1 方案設計

一個典型人臉識別系統的人臉特征數據庫包含了由已注冊用戶人臉特征組成的集合。當進行身份認證時，需要將測試人臉特征向量與集合中的各個人臉特征向量進行歐氏距離的計算，計算結果即為特征向量間的相異程度。假設待測試人臉的特征向量為x，集合中待匹配的人臉特征向量為y，將x和y之間的相異度定義為d(x,y)，那么d(x,y)為：

(1)

式中：n為所提取的人臉特征維度。

從式(1)可知，人臉的匹配過程包含了n個向量元素的減法(x1-y1)、n個向量元素的乘法(平方)和n個向量元素的累加求和。

在全同態加密方案中定義加密函數f對人臉特征z進行加密:ε(z)=f(z;θp)，其中θp為公鑰；同時z=g(ε(z);θs)，其中g(.;θs)為帶私鑰θs的解密函數。在保護原始人臉特征z的同時，也必須保證在加密域中進行計算而不會損失精度，即：

d(ε(x),ε(y))=d(f(x;θp),f(y;θp))

g(d(ε(x),ε(y));θs)≈d(x,y)

(2)

1.1 用戶注冊和身份認證協議

本節描述基于全同態加密方案的用戶注冊和身份認證協議。考慮具有兩個實體的場景：一個用戶和一個數據庫。

在系統初始化階段，需要執行以下步驟：生成一對公私密鑰對，公鑰為θp，私鑰為θs；將私鑰保存在認證服務器中，對外發布公鑰。

1.1.1注冊協議

在注冊階段，標識為c的用戶需要執行如下步驟：

(2) 使用公鑰θp加密用戶的人臉特征值yc，將人臉特征的同態密文ε(yc)與該用戶身份標簽一起保存到數據庫中。

注冊過程如圖1所示。

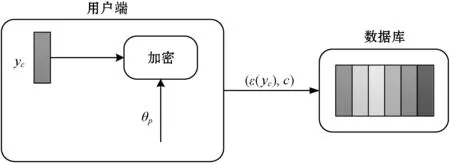
圖1 用戶注冊過程

1.1.2身份認證協議

在此階段，將通過以下步驟對用戶進行身份認證：

(1) 采集待認證用戶的人臉圖像并提取其特征值x，并使用公鑰θp加密。

(2) 計算待認證用戶的加密人臉特征ε(x)與數據庫中的所有加密人臉特征ε(y)之間的相異度d(ε(x),ε(y))。

(3) 使用私鑰θs分別對各個密文的計算結果進行解密，將滿足閾值要求的最小相異度對應的用戶身份標簽返回。

身份認證過程如圖2所示。

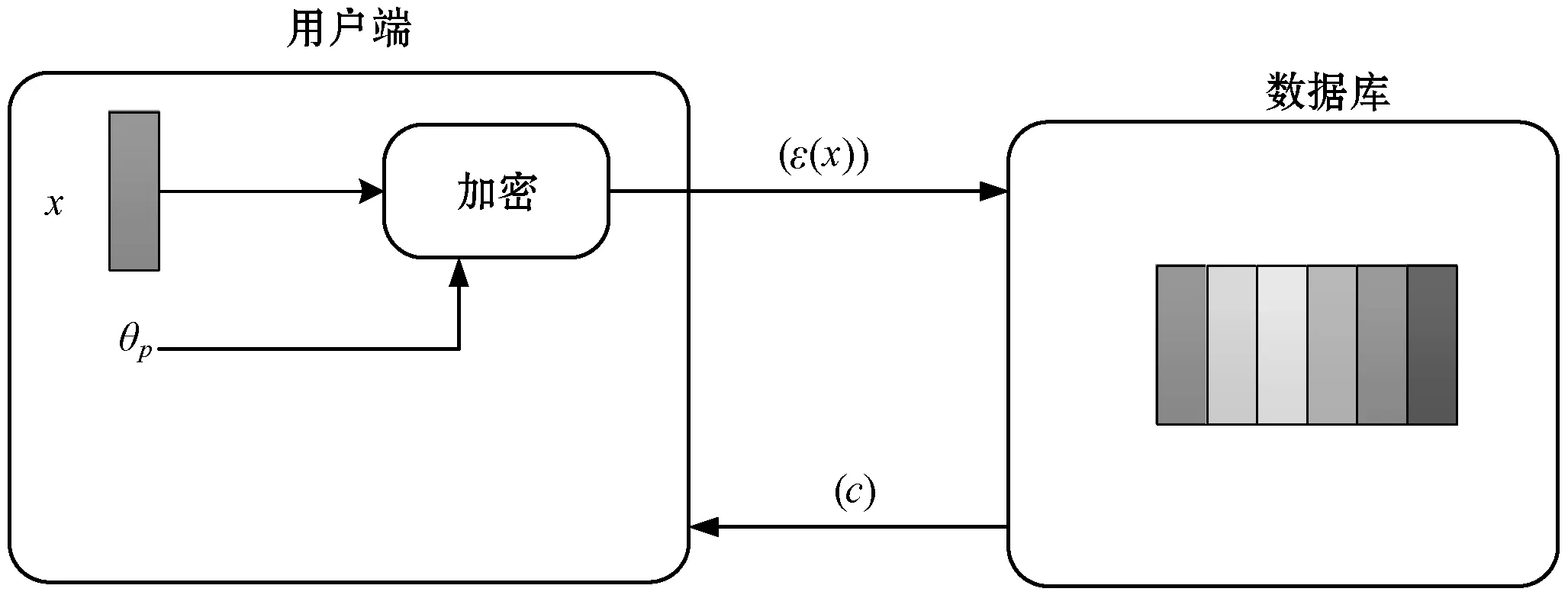
圖2 用戶身份認證過程

1.2 基于CKKS方案的高效人臉匹配

1.2.1全同態加密方案

由于人臉特征值是以浮點數表示，因此全同態加密選用支持浮點數的CKKS方案。

本系統的全同態加密方案包含以下5個步驟：

(1)GenKey(λ)：生成一對公私鑰。根據輸入的安全參數λ生成公鑰θp和私鑰θs。

(2)Encrypt(m,θp)：使用公鑰θp加密消息m，計算生成密文c。

(3)Add(c0,c1)：輸入兩個密文c0和c1，計算求得這兩個密文的和c0+c1。

(4)Multiply(c0,c1)：輸入兩個密文c0和c1，計算求得這兩個密文的乘積c0×c1。

(5)Decrypt(c′,θs)：根據密文c′，利用私鑰θs計算出明文m′。

1.2.2加密域中的人臉相異度的計算

式(1)中描述的人臉相似度可在加密域中描述為：

d(x,y)≈d(cx,cy)

(3)

式中：cx和cy分別為特征向量x和y的密文。d(cx,cy)的歐氏距離的計算為：

式中：n為人臉特征維度

該計算可分別為3個步驟：

(1) 對密文cx和cy進行減法運算：cz=Add(cx,-cy)。

(2) 對密文減法運算的結果進行乘法運算：cz=Multiply(cz,cz)。

(3) 最后還需要對cz中各個元素進行累加運算，得到歐氏距離的平方。由于全同態加密不支持平方根操作，因此在加密域中僅求得歐氏距離平方的密文。

那么在加密域中計算歐氏距離則需要n次的加密乘法運算和n-1次的加密加法運算。但由于每次對加密數據的乘法運算量很大，導致在加密域中計算人臉相似度的速度非常緩慢，尤其在人臉特征高維度表示的場景下該問題會進一步加劇。

1.2.3批處理

在加密域進行人臉匹配的主要瓶頸在于計算人臉相異度時所需的全同態加乘法次數與特征維度n呈線性關系。Brakerski等[10]提出了一種可針對數字向量進行同態加密和解密的技術，而不是每次僅使操作單個數字。該技術利用中國剩余定理(Chinese Remainder Theorem,CRT)將n個數編碼到同一個多項式上。那么對于兩個n維的人臉特征向量x和y，通過將包含n個向量元素的特征向量通過批處理整體加密至單個密文中，將n個向量元素密文的加法和乘法操作轉換為單個向量密文的加法和乘法操作，即在單次同態計算操作的時間內完成n次同態加法或乘法運算。因此，隨著一次批處理數量的增加，可顯著提高計算效率。通過批處理技術可完美完成加密域中人臉相異度計算的步驟(1)和步驟(2)。

但由于批處理方案是將向量整體加密，導致無法訪問加密后向量中的各個元素，也就無法完成步驟(3)中的各個元素累加運算，存在一定的局限性。但可以通過Gentry等[11]提出的循環旋轉logn次向量并累加，獲得加密向量中的各元素之和。

以4維向量為例，通過循環旋轉計算各元素和的過程如圖3所示。

對于512維的人臉特征向量，原先步驟(3)中511次同態密文的加法運算現在只需9次的循環和加法運算，進一步減輕了計算負擔。

綜上，基于CKKS方案的人臉匹配計算的實現關鍵代碼如下：

(1) 生成密鑰：

parms=EncryptionParameters(scheme_type.CKKS)

poly_modulus_degree=8192

parms.set_poly_modulus_degree(poly_modulus_degree)

parms.set_coeff_modulus(CoeffModulus.Create(

poly_modulus_degree,[60,40,40,60//))

context=SEALContext.Create(parms)

scale=pow(2.0,40)

keygen=KeyGenerator(context)

evaluator=Evaluator(context)

public_key=keygen.public_key()

secret_key=keygen.secret_key()

relin_keys=keygen.relin_keys()

gal_keys=keygen.galois_keys()

在本方案中使用的多項式模度poly_modulus_degree為8 192，配合近似最近鄰搜索方法中每個集合最多剩余4個點。

(2) 使用公鑰對人臉特征向量進行加密：

encryptor=Encryptor(context,public_key)

face_vector=np.loadtxt(data,delimiter=′,′)

inputs=DoubleVector(face_vector)

plain=Plaintext()

encoder.encode(inputs,scale,plain)

encrypted=Ciphertext()

encryptor.encrypt(plain,encrypted)

(3) 在加密域中計算人臉相異度：

#向量密文的減法操作，結果存入x_encrypted

evaluator.sub_inplace(x_encrypted,y_encrypted)

#向量密文的乘法操作，結果存入x_encrypted

evaluator.square_inplace(x_encrypted);

evaluator.relinearize_inplace(x_encrypted,relin_keys)

rotate_encrypted=Ciphertext()

result_encrypted=x_encrypted

#通過循環旋轉和累加計算元素密文和

i=1

while i<512:

evaluator.rotate_vector(result_encrypted,i,gal_keys,rotate_encrypted)

evaluator.add_inplace(result_encrypted,rotate_encrypted)

i*=2

(4) 使用私鑰獲取特征向量歐氏距離的平方和：

decryptor=Decryptor(context,secret_key)

plain_result=Plaintext()

decryptor.decrypt(result_encrypted,plain_result)

result=DoubleVector()

encoder.decode(plain_result,result)

return(result[0]**0.5)

1.3 基于Annoy搜索算法的人臉識別

人臉識別身份認證的過程就是將待認證用戶的人臉特征與數據庫中的所有人臉特征一一進行相異度的比較，將滿足閾值要求的最小相異度所對應的用戶身份標簽返回。倘若對每一個人臉都進行比較，那計算的時間復雜度為O(n)。由于相同的人臉得到的人臉特征索引都是比較類似，因此可以采用高效的Annoy(Approximate Nearest Neighbors Oh Yeah)算法對人臉特征創建索引。

Annoy算法的目標是建立一棵(群)二叉樹的數據結構，基于該數據結構能夠在較短的時間內找到任何查詢點的最近點，其查詢的平均時間復雜度為O(logn)。

(1) 建立索引。以2維數據集為例，Annoy算法首先隨機選擇兩個數據點，并以這兩個點為初始中心節點，執行聚類數為2的KMeans聚類，產生收斂后的兩個聚類中心點。在中心點的連線上(灰色短線)建立一條垂直線(黑色粗線)把數據空間分成兩部分。在多維空間中該黑色粗線即為等距垂直超平面。如圖4所示。

圖4 建立索引過程

然后在劃分的兩個子空間中繼續進行遞歸迭代，直到每個子空間中最多只剩下K個數據節點。在該方案中K值為4。

最終，通過多次遞歸迭代劃分，原始數據點會形成一個二叉樹結構。二叉樹的葉子節點記錄原始數據節點，中間節點則記錄的是分割超平面的信息。

(2) 查詢過程。完成索引建立之后，對一個數據點進行查找相似節點集合過程就是二叉樹的根節點不停向葉子節點遍歷的過程。通過對二叉樹每個中間節點(分割超平面相關信息)和查詢數據節點進行距離度量來確定二叉樹遍歷過程是繼續往這個中間節點的左子樹還是右子樹遍歷。

建立索引和查詢依賴于節點之間的距離度量。本方案在開源庫中歐氏距離方式的基礎上增加了全同態密文的歐氏距離度量方式，其實現代碼與在加密域中計算人臉相異度類似。二叉樹中間節點(等距垂直超平面)通過兩個聚類中心點各維度上的均值得到，在加密域中通過一次加法和乘法操作(乘以0.5)即可完成。

(3) 1 ∶K批量計算。上述查找過程完成后，返回的葉子節點中包含了至多K個人臉特征密文，最后還需要計算待認證用戶的人臉特征與該葉子節點中各個人臉特征的歐氏距離。

在全同態加密方式中使用的多項式模度poly_modulus_degree為8 192，其支持整體加密的向量長度最大為4 096。因此可通過旋轉操作將葉子節點中的所有人臉特征密文(以至多4個為例)構造于同一個密文中，合并后的密文結構如圖5所示。

圖5 合并后的密文結構

在合并后的密文結構中各個密文向量之間分別填充一個全0的512維向量，待認證用戶的人臉特征同樣構造上述密文結構，最后就可以利用批處理技術就可以同時計算單個待認證用戶人臉特征密文與K個人臉特征密文的歐氏距離。

2 系統測試

在系統仿真測試中基于人臉數據集(LFW)和基于深度神經網絡的人臉模型FaceNet(512維)進行測試。

本系統的服務端使用Python語言在Centos 7上開發，測試處理器為騰訊云單核2 GB配置的云服務器，CPU型號為Intel(R) Xeon(R) CPU E5- 26xx v4。同態加密算法采用微軟開源的簡單加密算法函數庫SEAL(Simple Encrypted Arithmetic Library)的Python版本PySEAL。

2.1 準確率測試

人臉數據集(LFW)中共包含了13 233幅人臉圖像，獲取數據集中的所有人臉特征信息后，將未加密情況下兩個人臉特征向量之間的歐氏距離與它們在加密域中計算出來的歐氏距離進行比較，部分數據如表1所示。

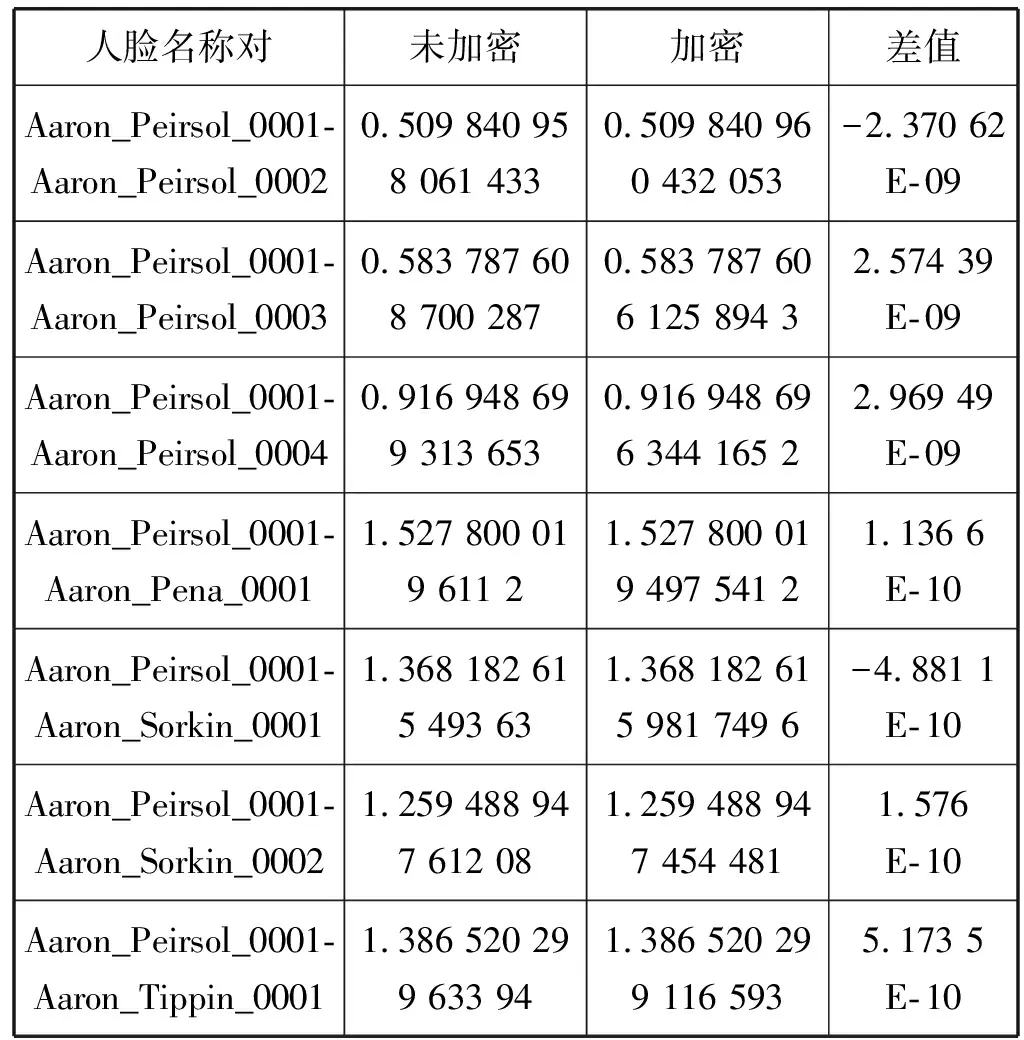
表1 未加密與加密人臉特征向量歐氏距離對比

從表1可知，加密后計算的人臉特征的歐氏距離能夠達到未加密人臉特征的水準，因此能夠保持原生算法的人臉識別準確率。

2.2 全同態性能

測試全同態計算過程中加密、歐氏距離計算(1 ∶4)和解密的用時情況，并與未加密情況進行對比，部分數據的操作用時如表2和表3所示。

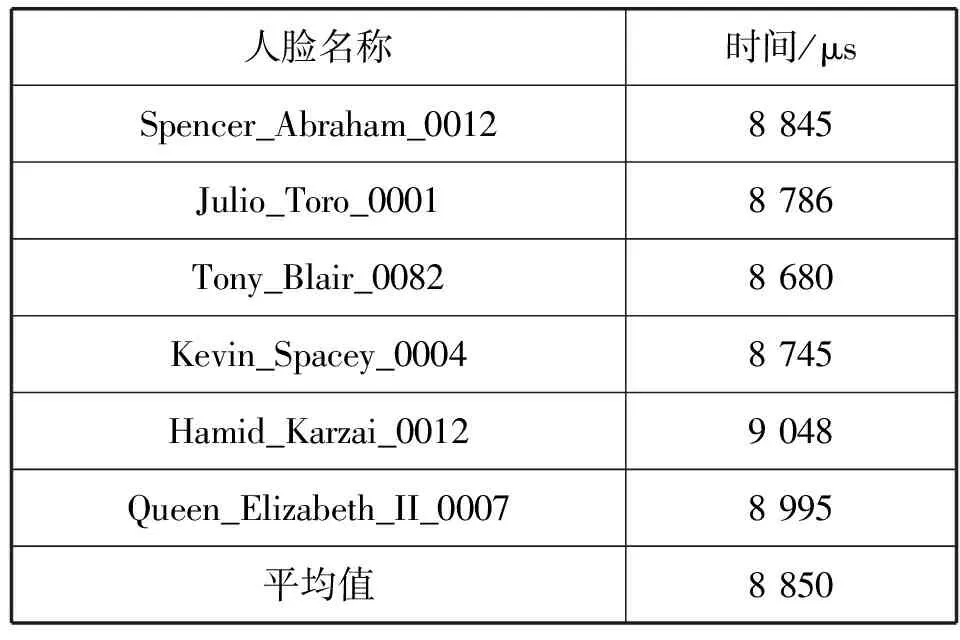
表2 加密過程用時

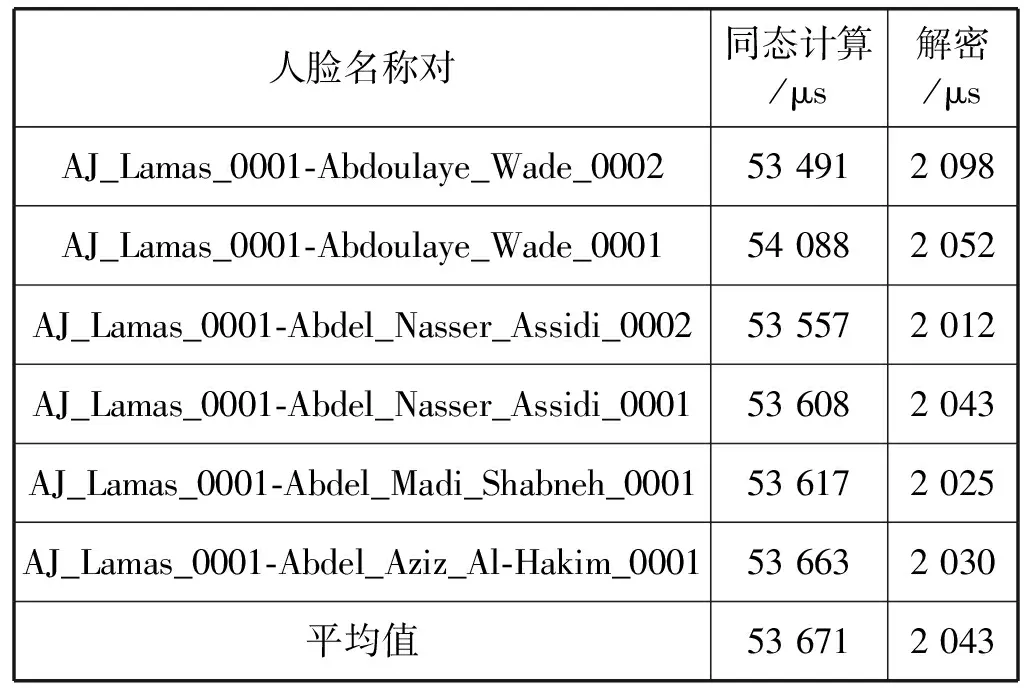
表3 加密域中同態計算和解密操作用時

從表2可知，在注冊過程中的人臉特征加密的平均用時為8 850 μs。

從表3可知，在認證過程中一對密文向量歐氏距離的同態計算用時平均為53 671 μs，密文解密時間平均為2 043 μs。在本方案的安全參數配置下，1 ∶4密文向量的同態計算用時與一對密文向量計算用時是一致的，因此在Annoy所建立的二叉樹中葉子節點中密文特征向量個數為4的情況下一對人臉特征密文歐氏距離的平均用時為13 418 μs。

未加密情況下一對人臉特征向量直接進行歐氏距離的平均用時為546 μs。綜上，未加密與加密情況下人臉特征距離的用時情況如表4所示。

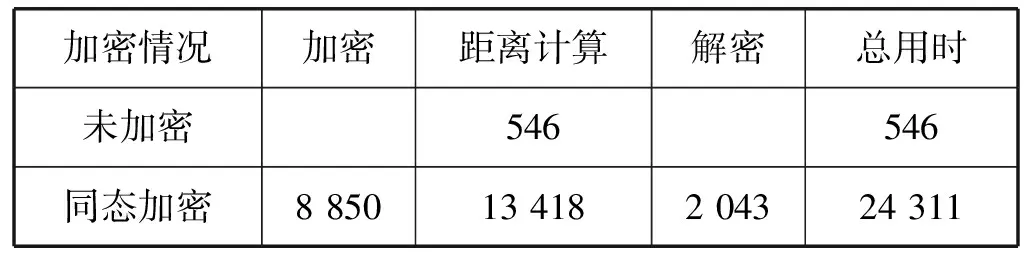
表4 未加密與加密情況下歐氏距離計算用時 單位：μs

從表4可知，在實驗環境中，使用全同態加密后一對人臉特征之間的歐氏距離計算的總用時大約為0.02 s，是未加密的45倍左右。

系統的整體架構為C/S架構，其中客戶端為用戶提供了注冊和登錄服務，服務器端提供了全同態計算和人臉認識服務。不考慮攝像頭采集人臉所花費的時間，以LFW數據集中的人臉模擬系統的注冊和登錄。加密前后人臉注冊的全過程用時如表5所示。

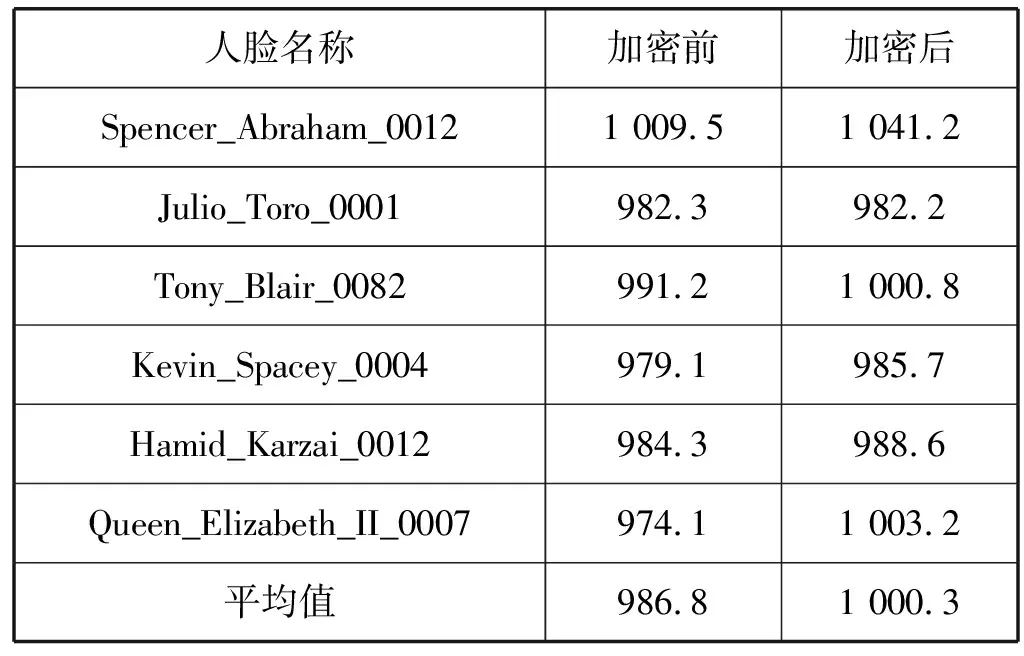
表5 注冊全過程用時 單位：ms

人臉數據庫中已存儲1 000個人臉特征密文，認證全過程用時如表6所示。

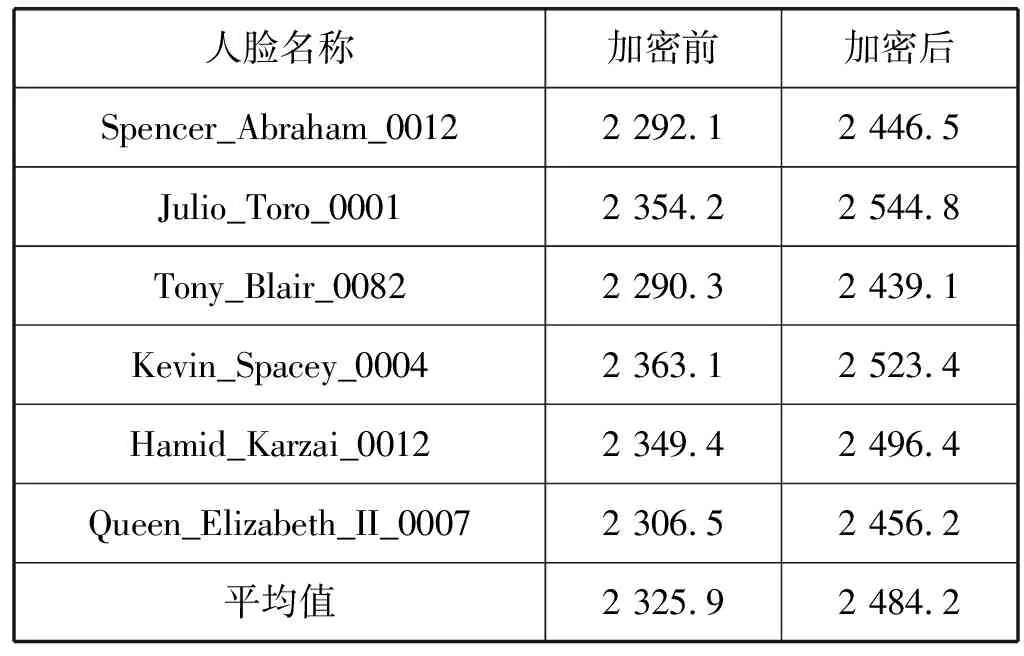
表6 認證全過程用時 單位：ms

測試結果表明：注冊過程中，加密后的平均用時為1 000.3 ms，相比加密前大約增加了13.5 ms，提高了不到2%，占注冊總用時的1.3%。而在認證過程中，加密后總用時平均為2 484.2 ms，相比加密前大約增加了158.3 ms，提高了6.8%，占認證總用時的6.37%。

從系統整體視角分析，圖形界面載入用時和網絡通信部分的用時最長，而同態加解密和計算用時占總用時大約5%。因此對人臉特征密文進行全同態計算的效率是能夠滿足實際應用需求的。

3 結 語

隨著信息技術的快速發展，信息安全已成為人們重點關注的領域。本文探討了使用全同態加密來保護人臉特征的實用性。首先，利用了一個批處理方案，實現了在單次同態計算操作的時間內完成n次同態加法或乘法運算，提高了在加密域中人臉匹配的效率；進一步利用近似最近鄰搜索算法，顯著提高了人臉識別的效率。在提供人臉模板保護、防止信息泄漏和保護用戶隱私的同時，基于全同態人臉的匹配能夠保持原生算法的人臉識別準確率，在性能上也可滿足實際應用的需求。