基于Hadamard 矩陣的最優局部修復碼構造

王 靜，田松濤，雷 珂，王相隆，任亞倩

(1. 長安大學信息工程學院 西安 710064；2. 西安郵電大學通信與信息工程學院 西安 710199)

隨著全球互聯網的全面普及，海量數據隨之產生，如何高效地管理和可靠地存儲海量數據成為當前的研究熱點。海量數據主要采用分布式存儲系統，為了維護系統的可用性和可靠性需引入冗余策略，最常見的冗余策略有復制策略和糾刪碼策略[1]，但都存在一定的局限性。隨后，文獻[2]將網絡編碼應用到分布式存儲系統中，提出了再生碼的概念。再生碼雖然在一定程度上減小了修復帶寬開銷，但修復故障節點過程中需連接大量存活節點，增加了系統的磁盤I/O 開銷。

為了解決上述問題，文獻[3]提出了局部修復碼(locally repairable codes, LRC)，有效降低了故障節點的修復局部性。文獻[4]研究了信息位具有局部性和可用性的局部修復碼的最小距離限，但關于修復局部性的邊界條件沒有研究。進一步地，文獻[5-6]分別研究了局部修復碼的構造并且協作局部修復碼，降低了存儲開銷并降低了修復局部性。文獻[7]研究了局部性為2 且可用性不等時的局部修復碼。

最小距離和碼率是衡量局部修復碼性能的兩個主要性能指標[8]，其中最小距離最優的局部修復碼一般簡稱為最優局部修復碼。文獻[9]利用射影平面和仿射平面理論構造了3 種局部性和可用性相等的局部修復碼，達到了最優最小距離邊界。基于部分幾何構造的最優局部修復碼[10]，通過交換點集和線集的關聯結構得到部分幾何的對偶，進而構造局部性和可用性不等的局部修復碼。基于Gilbert 方法的最優二元單校驗局部修復碼[11]，通過結合循環置換矩陣構造了一種新的LDPC 碼，將其與單位矩陣級聯形成校驗矩陣，進而構造出滿足最小距離界的二元單校驗局部修復碼。這3 種構造出的局部修復碼都可達到最優最小距離邊界，但是碼率較小。

除最小距離和碼率之外，在局部修復碼中也考慮維度這一參數。有學者基于生成矩陣、校驗矩陣和圖論相關理論構造局部修復碼來提高碼率，但都沒有分析維度是否達到維度最優的邊界條件。文獻[12]使用組合設計構造了最優二元局部修復碼，運用BIBD 和DBBD 區組設計構造出的局部修復碼在碼率上更優，但碼長略大。文獻[13]使用打包設計構造了最優局部修復碼，限制了碼長和維度的參數條件，無法靈活地構造不同情況下的局部修復碼。文獻[14]構造了最優單校驗二元局部修復碼，但其維度沒有達到維度最優的邊界條件。利用圖論相關理論來構造局部修復碼，主要是從二分圖的角度出發構造二元局部修復碼[15-16]，雖然能達到最優最小距離，但是構造算法略復雜。

針對以上問題，本文提出一種基于Hadamard矩陣的最優局部修復碼的構造方法。首先基于Hadamard 矩陣構造局部修復碼的校驗矩陣，通過校驗矩陣構造局部修復碼，構造的局部修復碼能達到最優最小距離界，但是維度沒有達到最優維度邊界條件。為了進一步提高維度，將校驗矩陣中的關聯矩陣0 和1 元素互換得到新的關聯矩陣，通過和新的關聯矩陣級聯進行擴展，構造的擴展局部修復碼不僅能達到最優最小距離界，且能達到維度最優的邊界條件。此外，基于Hadamard 矩陣構造的擴展局部修復碼的碼率也更逼近局部修復碼最優碼率的邊界，參數選擇更加靈活。

局部修復碼作為廣義上的糾錯碼，適用于分布式存儲系統。分布式存儲系統中存儲的文件采用局部修復碼進行編碼，并將編碼后的信息存于存儲節點中。當有部分存儲節點故障，則可以利用其余存活節點修復故障節點，實現分布式存儲系統中數據的可靠存儲。本節主要介紹局部修復碼的一些相關原理。

1.1 ( r,t)可用性

定義1[8]在有限域Fq上的 [n,k,d]q線性分組碼中，給定[n]={1,2,···,n} ， 碼字c=(c1,c2,···,cn)。如果其中一個編碼符號ci具 有局部性r和可用性t，需滿足下列條件：

稱φj(i)(j∈[t])為ci的修復集合。如果局部修復碼的所有信息位碼元都具有 (r,t)可用性，那么稱該碼為具有 (r,t)可 用性的局部修復碼，記作(n,k,r,t)iLRC。若每個信息位碼元的每個修復集只有一個校驗位碼元，則這個碼稱作單校驗 (n,k,r,t)iLRC。本文主要研究單校驗 (n,k,r,t)iLRC，該碼由關聯矩陣和單位矩陣拼接而成，其中關聯矩陣的行重為局部性r，列重為可用性t。

1.2 最小距離

定理1[10]若一個線性分組碼C是信息位具有局部性r和可用性t的局部修復碼，最小距離應滿足：

定理2[13]若局部修復碼的所有信息位碼元的每一個修復集中只含有一個校驗位，且該單校驗(n,k,r,t)iLRC 的最小距離滿足：

1 局部修復碼相關概念

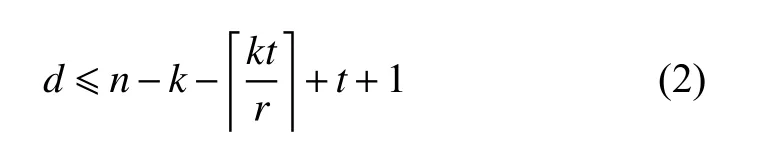
稱達到邊界(2)的局部修復碼是最小距離最優的單校驗(n,k,r,t)iLRC。

1.3 碼率和維度

一般地，每個碼的信息位個數k與碼元數n之間的比值稱作碼率，用R=k/n表示。

定理3[17]若 (n,k,r,t) L RC 具有 (r,t)可用性，且該碼碼率滿足：

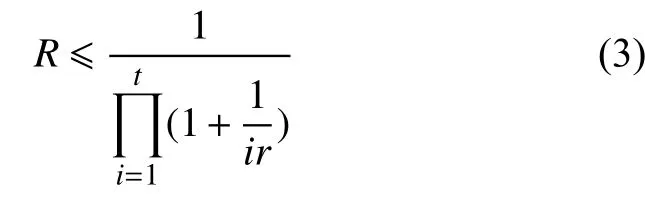
則達到邊界(3)的局部修復碼的碼率最優。

定理 4[18]特別地，可用性t=2的最優碼率的(n,k,r,t=2)單校驗局部修復碼滿足的碼率邊界條件為：

定理 5[19](維度C-M 邊界限)在有限域GF(q)中的(n,k,r)單校驗局部修復碼的維度應滿足：

2 最優局部修復碼的構造

2.1 基于Hadamard 矩陣的局部修復碼構造

構造基于Hadamard 矩陣的局部修復碼，關鍵在于構造局部修復碼的校驗矩陣。局部修復碼的校驗矩陣用H=[M|I]表 示，I是單位矩陣，單位矩陣的列對應局部修復碼的校驗位符號；M是對應的關聯矩陣，關聯矩陣的列對應信息位符號。碼字和校驗矩陣的關系為c·H⊥=0，通過此關系可知每個信息位碼字的修復集，一個基于校驗矩陣構造的具有可用性(r,t)的 局部修復碼，它的關聯矩陣的行重r用來保證局部性，列重t用來保證可用性。

本節主要基于Hadamard 矩陣構造關聯矩陣，關聯矩陣級聯單位矩陣生成校驗矩陣，通過校驗矩陣來構造局部修復碼。

定義2k′階 方陣Hk′，若其元素為1 或-1，且滿足：

稱Hk′為k′階 Hadamard 矩陣，其中Ik′是k′階單位陣。

若Hk′首 行首列均為全1 向量，則該Hk′為標準Hadamard 矩陣。本文所涉及的Hadamard 矩陣均為標準Hadamard 矩陣。

5) 將矩陣H(2k′-1)×(4k′-2)作為局部修復碼的校驗矩陣，構造得到(n=4k′-2,k=2k′-1,r=k′,t=k′)局部修復碼，其中可用性t為2 的倍數。

推論1 構造1 中(n=4k′-2,k=2k′-1,r=k′,t=k′)局部修復碼為最小距離最優的局部修復碼，且碼的最小距離d=t+1。

證 明：將 (n=4k′-2,k=2k′-1,r=k′,t=k′)局部修復碼的參數代入邊界條件(2)，有：

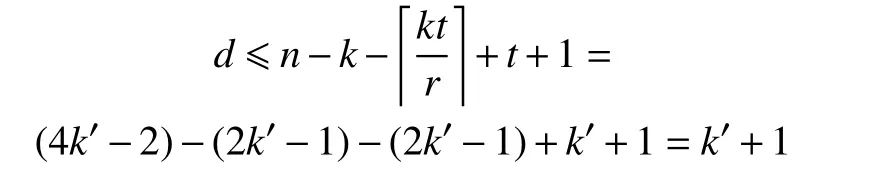
因 為k′=t，則d≤t+1。 又 根 據 式(1)得d≥t+1， 所以d=t+1，可得到基于Hadamard 矩陣構造的局部修復碼的最小距離d=t+1，滿足邊界條件(2)，則該碼是最小距離最優的局部修復碼。

構造1 中的局部修復碼的碼率R=n k= 1

2，沒有達到式(3)中最優碼率的邊界條件，故該碼不是碼率最優的局部修復碼。

例1 令k′=4，得到方陣：

利用步驟 2) 可得到M8×8， 將M8×8的首行和首列全部刪除，得到一個7 階的關聯矩陣M7×7：

2.2 基于Hadamard 矩陣的擴展局部修復碼構造

上述基于Hadamard 矩陣構造的局部修復碼的局部性和可用性相等，且能夠達到最優最小距離界，但是該局部修復碼的碼率較小，沒有達到維度最優的邊界條件。為了進一步提高碼率和維度，將上述構造中的關聯矩陣M(2k′-1)×(2k′-1)進行擴展，得到碼率更高并且維度最優的擴展局部修復碼。

構造2 基于Hadamard 矩陣的擴展局部修復碼的具體構造步驟如下。

1) 首先將Hadamard 矩陣的1 元素全部換為0 元素，-1 元素全部換為1 元素，得到一個k′階方陣，記為Mk′×k′；

2) 根據k′階 方陣Mk′×k′構造：

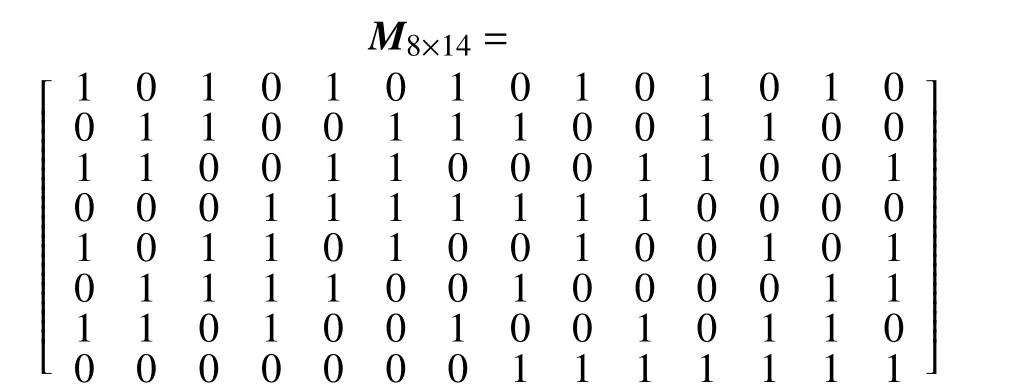
最后將M8×14作為擴展局部修復碼的關聯矩陣，和 單 位 矩 陣I8級 聯 生 成 校 驗 矩 陣H8×22=[M8×14|I8]， 由 此 可 構 造 出 單 校 驗(n=22,k=14,r=7,t=4)局 部修復碼，此碼的最小距離d=5，碼率R=7/11，與構造1 相比，有效地提高了局部修復碼的碼率。

故障節點的修復方法為：若信息位c1發生故障，由c·HT=0 可知，信息位c1可 根據c1=c15-c3-c5-c7-c9-c11-c13=c17-c2-c5-c6-c10-c11-c14=c19-c3-c4-c6-c9-c12-c14=c21-c2-c4-c7-c10-c12-c13進 行修復，那么信息位c1的修復集可表示為φ1={3,5,7,9,11,13,15} ，φ2={2,5,6,10,11,14,17} ，φ3={3,4,6,9,12,14,19} 和φ4={2,4,7,10,12,13,21}，各 個修復集都只有一個校驗位符號。同理，其他信息位符號也可用相同的方法進行修復。

3 性能分析

3.1 最小距離和維度分析

推論2 構造2 得到的(n=6k′-2,k=4k′-2,r==2k′-1,t=k′)局部修復碼是最小距離最優的局部修復碼，且碼的最小距離d=t+1。

證明：將(n=6k′-2,k=4k′-2,r=2k′-1,t=k′)局部修復碼的參數代入邊界條件(2)，可得：

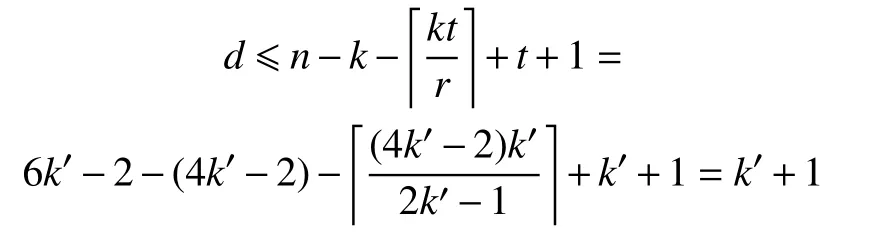
因為k′=t，即d≤t+1。 又根據式(1)得d≥t+1，所以d=t+1，可以得到構造2 中的局部修復碼的最小距離d=t+1。該局部修復碼的最小距離滿足邊界條件(2)，則該碼是最小距離最優的局部修復碼。

推論3 構造2 得到的(n=6k′-2,k=4k′-2,r=2k′-1,t=k′)局部修復碼是維度最優的局部修復碼，且碼的維度k≤4k′-2。

證明：當式(1)中最小距離d為最大值時，可以將式(5)簡化如下：

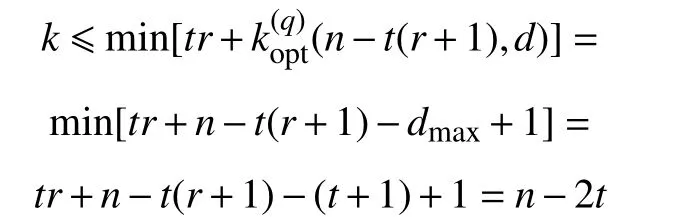
將(n=6k′-2,k=4k′-2,r=2k′-1,t=k′)LRC 的參數條件代入簡化的公式中，可得k≤4k′-2，對于?k′，基于Hadamard 矩陣構造的擴展局部修復碼的維度都可達到最優維度邊界條件的上界。

3.2 與現有局部修復碼的對比分析

基于Hadamard 矩陣構造的擴展局部修復碼的碼率為：

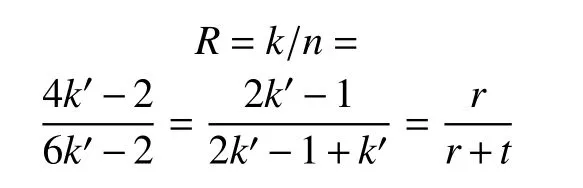
則本文構造2 中局部修復碼的碼率大于基于直積碼構造的局部修復碼碼率。

表1 不同局部修復碼參數對比

圖1 所示為t=4時，不同局部修復碼的碼率R隨著局部性r的變化曲線，也容易看出構造2 的碼率是最逼近局部修復碼最優碼率界限的。

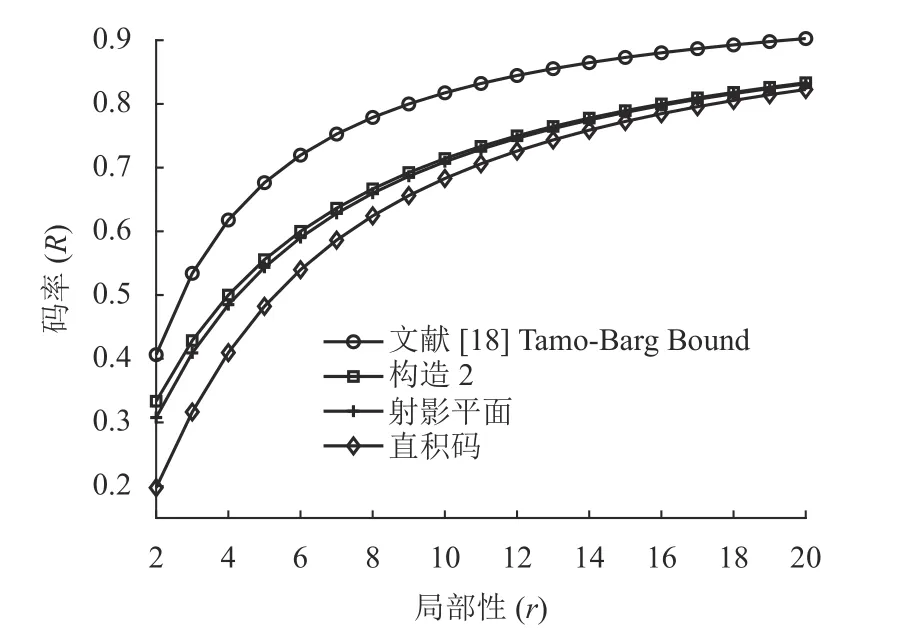
圖1 t =4情 況下，碼率R 的對比

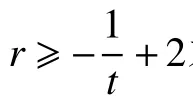
表2 不同局部修復碼關于維度參數的對比

4 結 束 語

為了滿足在最優最小距離邊界條件下，局部修復碼的維度也能達到最優，本文首先構造了基于Hadamard 矩陣的局部修復碼，此局部修復碼能達到最優最小距離界，但是維度沒有達到維度最優的邊界條件。為了提高維度，將校驗矩陣中的關聯矩陣0 和1 元素互換得到新的關聯矩陣，通過和新的關聯矩陣級聯進行擴展，構造的擴展局部修復碼不僅能達到最優最小距離界，且能達到維度最優的邊界條件。將基于Hadamard 矩陣構造的擴展局部修復碼和現有的局部修復碼相比，本文的構造在碼率上更逼近局部修復碼最優碼率的界限。

本文得到長安大學大學生創新創業訓練計劃項目(G202010710031)資助，在此深表感謝！