K-Means 算法最優(yōu)聚類數量的確定

何選森，何 帆，徐 麗，樊躍平

(1. 廣州商學院信息技術與工程學院 廣州 511363；2. 湖南大學信息科學與工程學院 長沙 410082；3. 北京理工大學管理與經濟學院 北京 海淀區(qū) 100081)

在大數據時代[1]，數據分類是數據應用的基礎，由于無監(jiān)督的分類(unsupervised classification)或聚類(clustering)[2]不需要對數據進行訓練，因而獲得了廣泛應用。聚類是采用多元統計方法，依據數據間的相似性或距離測度直接把性質相近的數據歸為一類，性質差異較大的樣本歸屬于不同的類。聚類分析中的聚類結構有3 種：分區(qū)(partitional)聚類、層次(hierarchical)聚類和單個(individual)集群。層次聚類又分為凝聚層次聚類[3]和分裂層次聚類[4]。常用的聚類法有模糊C 均值聚類[5]、密度基(density-based)聚類[6]以及K-均值(K-Means)類的聚類[7]等。

在無先驗知識情況下對數據分析的關鍵是找出數據中的固有劃分(inherent partitions)，盡管聚類算法可以劃分數據，但不同算法或同一種算法采用不同的參數將產生出不同的數據劃分或揭示不同的聚類結構(clustering structures)。因此，客觀、定量地評價算法的聚類結果就顯得十分重要。換句話說，由一種聚類算法得到的聚類結構是否有意義，即聚類驗證(cluster validation)非常重要。層次聚類是基于鄰近矩陣(proximity matrix)將數據組織到層次結構中，其結果通常用樹狀圖[8]表示。與層次聚類相比，分區(qū)聚類將一組數據對象分配到沒有任何層次結構的k個聚類中[9]，而且這個過程通常伴隨著對一個準則函數的不斷優(yōu)化。在分區(qū)聚類算法中，應用最廣泛的一種準則函數是平方誤差和準則(sum-of-squared-error criterion)[2]。使得平方誤差和為最小的劃分被認為是最優(yōu)的，一般稱其為最小方差(minimum variance)劃分[7]。數據的聚類是指：在同一類中數據對象具有很高的相似度(similarity)，而不同聚類之間的數據則具有較高的相異性(dissimilarity)[10]。顯然，相似性與相異性(或稱距離)可概括為鄰近性，它既可以描述數據點之間、數據類之間的遠近關系，又可以描述數據點與數據類之間的遠近關系。對于聚類分析，常用的距離是歐幾里得(歐氏)距離，利用歐氏距離形成的聚類對特征空間中的平移和旋轉變換具有不變性[11]。

1 K-均值算法與聚類有效性分析

K-均值屬于分區(qū)聚類的結構，目標是將數據組織成若干類，并且任一數據點只能屬于一個類而不能同時屬于多個類，這就意味著K-均值算法生成的是特定數量、互不相交、非層次的聚類。K-均值算法通過迭代優(yōu)化步驟，利用最小化平方誤差和準則來尋求數據的最佳劃分，屬于爬山(hill-climbing)類算法的范疇[7]。本質上，K-均值就是期望最大化(expectation maximization, EM)算法的經典范例。EM 算法的第一步是尋找與聚類相關的期望點，第二步是利用第一步的知識改進對聚類的估計，重復這兩個步驟直到算法收斂。

K-均值算法中，數據對象之間采用歐氏距離來度量相異性。設數據集有n個樣本，它的p維觀測為：

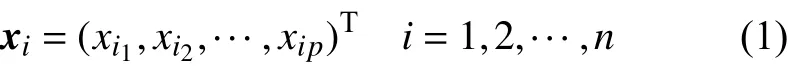
任意兩個樣本點xi,xj(i,j=1, 2, ···,n)之間的歐氏距離表示為dij=d(xi,xj)。如果將n個樣本分成k個聚類，則選擇全部數據之間距離最遠的兩個(序號為i1,i2)樣本作為初始聚類中心(聚點)：

然后再確定下一個聚點(序號i3)，使得i3與i1,i2距離最小者等于所有其他點與i1,i2較小距離中的最大者：

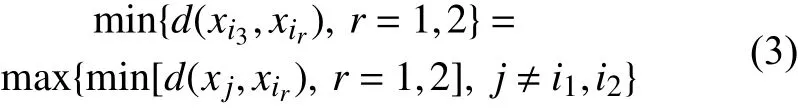
不斷重復以上過程，即可確定全部k個初始聚點。因此，K-均值算法的基本過程可以歸納如下。

1) 設隨機選取的k個初始聚點的集合為：

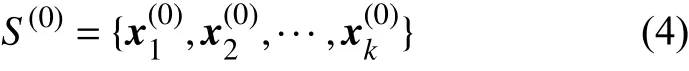
對于任意的數據點x，對它的劃分原則為：

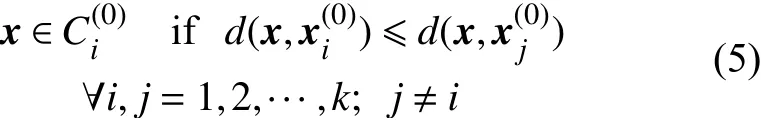
即將所有樣本分成不相交的k個類，得到初始分類：

顯然，K-均值聚類算法的基本思想是將數據空間首先隨機地劃分為事先指定的k個類，然后通過迭代計算不斷更新每個類的質心。當相鄰兩次迭代計算的結果基本相同時，則算法收斂。盡管K-均值算法被證明是收斂的[12]，然而困擾K-均值聚類的第一個問題是它的迭代優(yōu)化過程不能保證算法收斂到全局最優(yōu)。由于K-均值算法可以收斂到局部最優(yōu)[7]，不同的初始劃分將導致不同的收斂質心。第二個問題是K-均值算法對數據中的異常值也即野值(outliers)以及噪聲(noise)很敏感[2,7]，在迭代計算聚點的過程中算法卻是考慮了所有的樣本。即使某個樣本點離質心很遠，但K-均值算法仍然將該點強行納入最鄰近的類中用于計算其質心，這樣就造成了聚類形狀的扭曲。另外，K-均值類算法要求用戶事先指定聚類數量，這在實際中很難做到。聚類數量是否正確將直接影響聚類效果，確定最優(yōu)的聚類數量也稱為聚類有效性分析(clustering validity analysis)[13]。因此，在聚類分析中，一個必不可少的步驟是驗證聚類結果并確保它能正確地反映數據的本質結構。基于統計理論對算法生成的聚類結構進行評估，強調以客觀和定量的方式對聚類結果進行評價，這就是聚類趨勢分析(clustering tendency analysis)[14]。

分區(qū)聚類、層次聚類和單個集群的結構所對應的聚類有效性測試標準分別為外部的(external)、內部的(internal)和相對的標準(relative criteria)[15]，這3 種標準的適用范圍不同。外部與內部標準都涉及到統計方法和假設檢驗[16]，這將導致計算開銷增加。而相對標準則無須進行統計檢驗，它致力于比較不同的聚類結果。因此，相對標準可用于比較K-均值類算法一系列不同聚類數量k的聚類效果，以便找出數據劃分最適合的k值，這個問題也被稱為聚類有效性的基本問題(fundamental problem)[17]。

K-均值類算法包括一系列聚類方法，如Kmedoids 算法[18]和K-均值算法，它們的適用范圍和特點各不相同。K-均值的時間復雜度為O(nkpT)，其中，n為樣本數量，k為聚類數量，p為數據維數，T為算法迭代次數，由于k,p,T通常都比n小很多，因此K-均值的時間復雜度為近似的線性關系[2,7]，因而它以低計算復雜度體現出高效率[18]，但它的聚類結果很大程度上受數據中噪聲與異常值的影響。為了解決K-均值算法的這個缺陷，Kmedoids 算法以中心點(medoids)作為聚類中心，對噪聲及異常點處理能力優(yōu)秀且具有較強的魯棒性。然而它的缺點是計算復雜度較高，因此學者們致力于改進K-medoids 算法，以期在計算效率上追趕K-均值算法[18]。在眾多改進的K-medoids 方法中，圍繞中心點劃分(partitioning around medoids,PAM)算法[19]被認為是最有效的K-medoids 算法之一。但PAM 算法的迭代次數較多，時間效率低[19]。在不考慮迭代次數的情況下，K-medoids 和PAM算法的時間復雜度都為O(k(n-k)2)[18]，即為二次函數。對于這3 種經典的K-均值類聚類算法，僅從時間開銷的角度來看，K-均值算法的計算速度是最快的。另外，這3 種算法的共同缺點仍是聚類數量k作為算法的參數必須事先指定。聚類數量k過大或過小的估計都將嚴重影響最終的聚類質量。過多的聚類數量造成真正的數據聚類結構變得復雜，使得對聚類結果的解釋和分析變得困難，而過少的聚類數量將損失信息并造成錯誤的聚類結果。

本文主要研究經典K-均值聚類算法中最佳聚類數量的確定問題，因此，其基本的思路為：對于具體的數據集，首先在聚類數量的可能范圍內，采用不同的聚類數量來運行K-均值算法以獲得相應的聚類結果；然后以聚類數量k為自變量構造一種聚類有效性函數(指標)對K-均值的聚類結果進行評估，通過優(yōu)化聚類有效性函數來確定最優(yōu)的聚類數量。

2 聚類有效性評價函數

對于理想的聚類效果，從相似性角度要求類內樣本點之間盡可能相似，同時類與類之間的樣本點盡可能相異。從距離的角度則要求類內樣本點之間距離的代數和應盡量小，而在不同類之間樣本點距離的代數和應盡量大。在整個數據空間中，樣本點與它所在類的聚點之間的距離，要比它與其他類的聚點間的距離都要小。滿足這個條件的聚類就是有效的數據劃分。

對于全部的n個數據點，其樣本均值(質心)為：

在所有的數據中，假設第i個聚類Ci中有ni個數據對象，則定義該類的樣本質心(中心)為：

從定義1 的表達式可看出，當所有樣本都屬于同一個類(即聚類數量k=1)時，則這個類的中心就是全體數據的質心xˉ。在這種情況下，類間質心距離之和Dbetw取值為0，即取Dbetw(k)的極小值。隨著聚類數量k的增加，類間質心距離之和函數Dbetw(k)是遞增的。

定義2 類內距離之和 在聚類空間I 上，由每個類中的各樣本到該類中心的歐氏距離之和為同一類的內部距離，而所有k個聚類的內部距離之和則定義為類內距離之和：

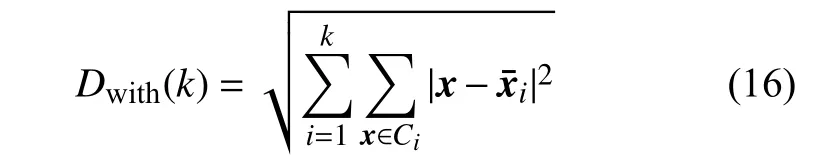
從定義2 可知，當整個數據集的樣本屬于同一個類(聚類數量k=1)時，Dwith就是所有數據點與其質心xˉ的距離之和，即取Dwith(k)的極大值。隨著聚類數量k的增加，類內距離之和函數Dwith(k)是遞減的。

定義3 聚類有效性評價函數 在聚類空間I上，基于類間質心距離之和Dbetw與類內距離之和Dwith，定義一種綜合評價函數(指標)：

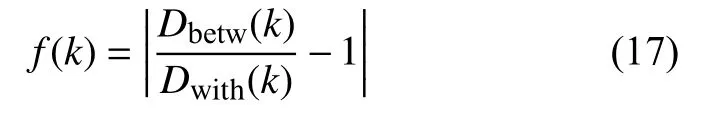
式中，|?|表示取絕對值。當所有數據樣本點都屬于同一類(聚類數量k=1)時，由于Dbetw(k)=0，則f(k)=1。顯然，隨著聚類數量k的變化，函數f(k)的值也發(fā)生相應變化，即f(k)是以聚類數量k為自變量的函數。對于K-均值算法，最好的聚類效果意味著聚類數量k是最優(yōu)的，因此將f(k)稱為聚類有效性評價函數(指標)。

在統計學中，經驗規(guī)則(empirical rules)[20]常用來預測最終的結果，它也稱為3σ 規(guī)則或68-95-99.7 規(guī)則。經驗規(guī)則表明：對于正態(tài)分布，幾乎所有的觀測數據X都將落在平均值E[X]的3 個標準差σ 之內。具體地說，68%的數據落在平均值的1 個σ 之內，95%的數據落在平均值的2 個σ 之內，99.7%的數據落在平均值的3 個σ 之內[21]。在某些情況下，獲取數據的分布可能很耗時，甚至是不可能的，因此正態(tài)概率分布可以作為一種臨時啟發(fā)式(heuristic)方法，如當一家公司正在審查其質量控制措施或評估其風險暴露(risk exposure)時，風險價值(value-at-risk)作為常用的風險工具，假設風險事件的概率服從正態(tài)分布，對于服從其他分布的觀測數據來說，將經驗規(guī)則推廣為經驗貝葉斯規(guī)則(empirical Bayes rules)[22-23]，則可實現對具有k類的觀測數據總體進行推斷。因此，在計算出數據的均值和標準偏差之后，經驗規(guī)則可用于粗略地估計觀測數據總體中所隱含的數據類k的數量范圍。

定理 最佳聚類數量準則 在聚類空間I 上，根據經驗規(guī)則，可以估計出聚類數量k可能的最小值kmin和最大值kmax，因而獲得k的取值范圍[kmin,kmax]。當k在[kmin,kmax]變化時，如果聚類有效性評價函數f(k)獲得最小值，則K-均值算法的聚類效果為最優(yōu)，即對應的最佳聚類數量k為：

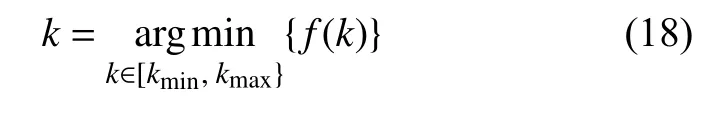
證明：由定義1 可知，類間質心距離之和Dbetw(k)是聚類數量k的單調增函數，由定義2 可知，類內距離之和Dwith(k)是k的單調減函數。因此隨著k取值的變化，由定義3 可知，聚類有效性評價函數f(k)存在極小值，但并不存在有限的極大值。換句話說，函數f(k)可能取值為無窮大，此時對應的聚類數量k是不合理的。

在實際應用中，聚類數量k只能取正整數，而且函數Dbetw(k)和Dwith(k)也都只能取正實數值(非負值)。在k的有限取值范圍[kmin,kmax]內，函數f(k)一定存在有全局的極小值，即最小值。顯然，聚類有效性評價函數的最小值所對應的k值就是數據集的最優(yōu)聚類數量。由定義3 可知，只有當Dbetw(k)和Dwith(k)的取值相等或二者非常接近時，函數f(k)才能取得最小值。換句話說，通過調整聚類數量k的取值使得Dbetw(k)和Dwith(k)達到最接近的程度，K-均值聚類的效果才是最佳的，此時對應的聚類數量k值就使得數據的分類達到最優(yōu)。因此，利用聚類有效性評價函數f(k)作為確定最佳聚類數量k的準則，也就是確定f(k)的最小值準則。

為了找到K-均值算法的最佳聚類數量k，從可視化的角度，在k值的可能變化范圍[kmin,kmax]內，通過繪制聚類有效性評價函數f(k)隨聚類數量k的變化曲線，直觀地搜尋函數f(k)的最小值點所對應的聚類數量k，即為最佳的聚類數量。

3 驗證與分析

為了驗證本文提出的聚類有效性評價函數的性能以及由此獲得的最佳聚類數k是否符合數據本身內在的分類結構，利用加州大學歐文分校的機器學習庫(UC Irvine machine learning repository)中的多個數據集進行仿真實驗。

仿真PC 機的CPU 為：Intel(R) Celeron(R)1007U-1.5 GHz，內存4 GB，操作系統為Windows 10，仿真是在MATLAB 9 (R2016a)上運行。

對于數據的分類與聚類問題，最常用的UCI數據集有Iris、Seeds 和Wind 數據集。這3 種數據集的數據樣本數量、屬性(特征)數量以及數據真實的聚類數量如表1 所示。

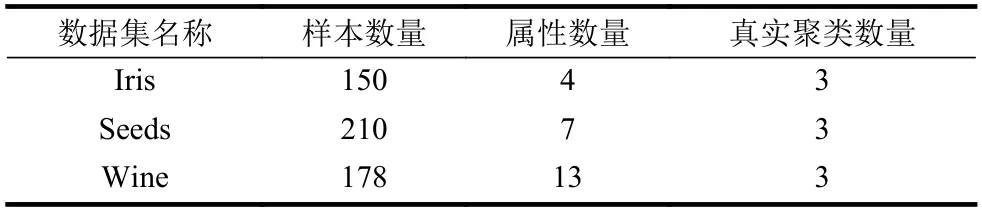
表1 3 種UCI 數據集的有關信息

仿真的基本過程為：對于每一種數據集，根據經驗規(guī)則估計數據的可能聚類數量范圍[kmin,kmax]。在這個范圍內的每個k值，首先分別運行K-均值算法一次，并計算相對應的聚類有效性評價函數f(k)。然后多次運行K-均值算法以觀察函數f(k)的變化趨勢，從而對聚類有效性評價指標f(k)的平均性能進行測試。

3.1 數據集Iris 的仿真

鳶尾花Iris 數據集記錄了3 種花setosa、versicolor 和virginica 的4 種屬性，即萼片長(sepal length)表示為x1、萼片寬(sepal width)表示為x2、花瓣長(petal length)表示為x3、花瓣寬(petal width)表示為x4。3 種花各記錄了50 組特征(即屬性)的數據，按照setosa、versicolor 和virginica 的順序存放。

為了觀察Iris 數據集對應特征的統計中心位置，即不同屬性值的分布范圍所圍繞的大致中心，首先計算出每種鳶尾花的4 個屬性，即變量x1,x2,x3,x4的均值，如表2 和圖1 所示。

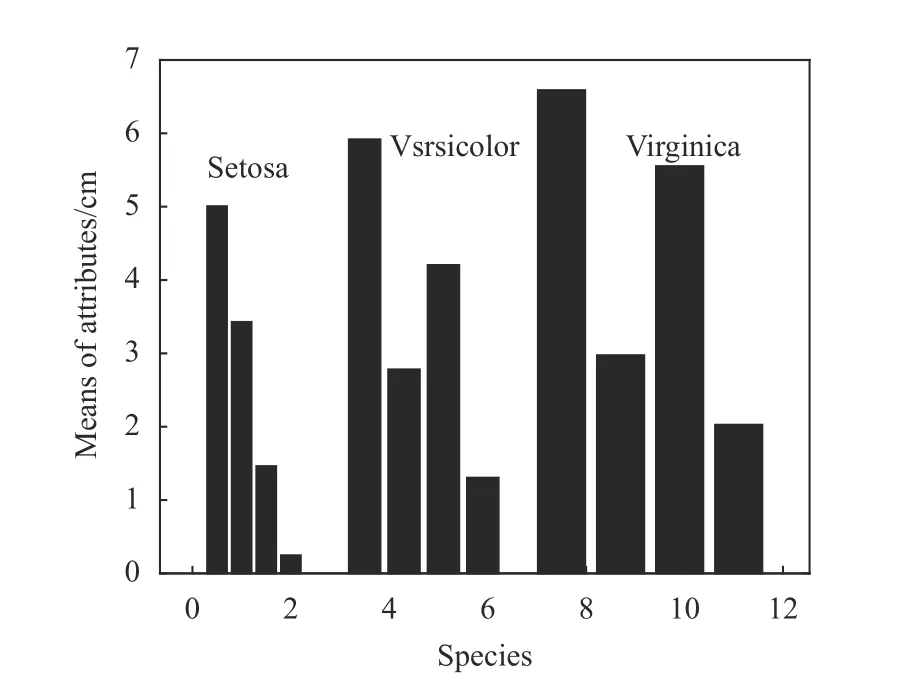
圖1 3 種鳶尾花特征變量均值的條形圖

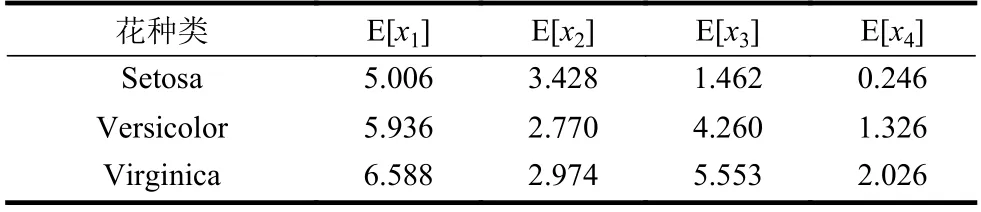
表2 3 種花4 個屬性的均值 cm

根據數據樣本數量以及經驗規(guī)則，設Iris 數據可能的聚類數量范圍為[kmin,kmax]，其中kmin=2，kmax=12。對于[kmin,kmax]中的每個k值，運行K-均值算法一次，并計算出相對應的聚類有效性評價函數f(k)的值，其結果如表3 和圖2 所示。

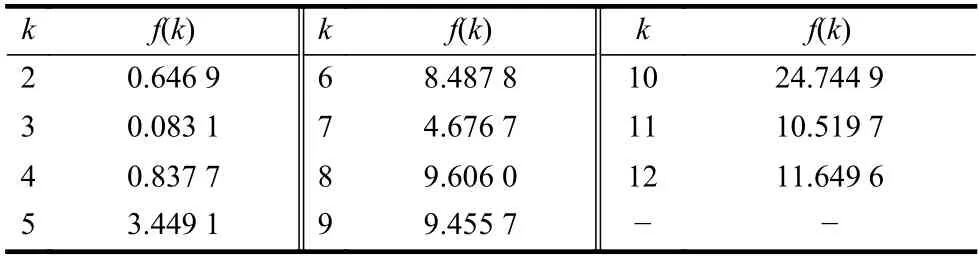
表3 Iris 數據的f(k)與k 的對應表

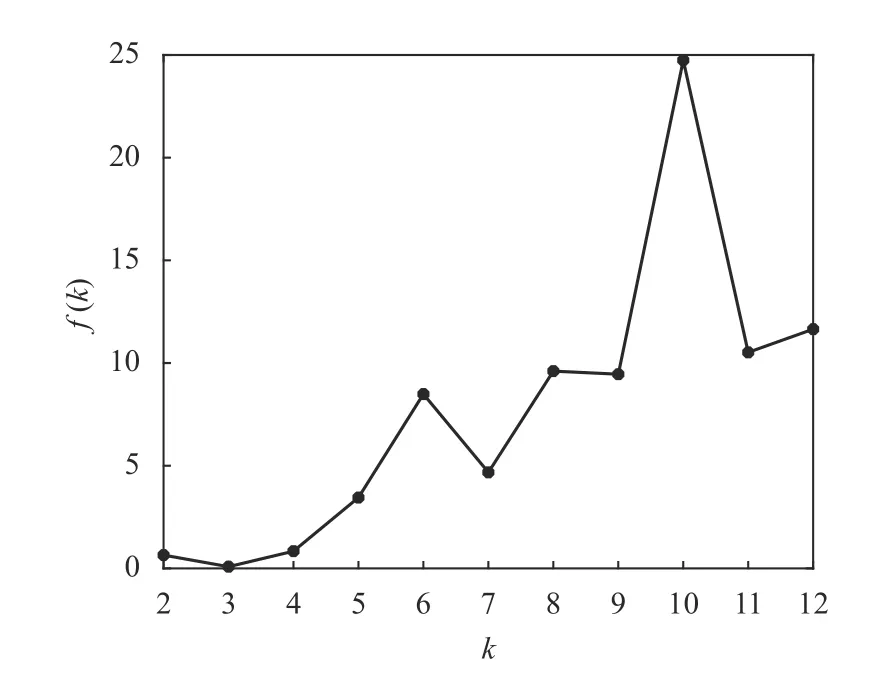
圖2 Iris 數據的f(k)隨聚類數量k 的變化曲線

從圖2 和表3 可以看出：1)函數f(k)隨著k值做相應變化，這就說明聚類有效性評價函數f(k)用來對聚類數量k的選擇進行評價是有效的；2)當k=3 時，f(k)取得最小值，即最佳的聚類數量為3。這個結果證明聚類有效性評價函數f(k)能夠從Iris 數據集中找出最佳的聚類數量，即真實的鳶尾花所包含的種類。

這里需要說明，K-均值算法的另一個缺陷是它可以收斂到局部最優(yōu)，而且每次運行K-均值算法時，初始的聚類中心是從所有數據中隨機選取的。因此算法要求必須有一個合理的初始化，在實際應用中這是不現實的。對于不同的初始劃分，將導致K-均值算法收斂到不同的質心位置。一種解決方案是通過重復運行K-均值算法多次，并以多次運行的平均結果來降低隨機初始化的影響。為此，將K-均值算法按照上述的仿真條件重復運行10次，每次分別記錄下對應的聚類有效性評價函數f(k)的值。為觀察方便，這里僅繪制出每次運行中函數f(k)隨聚類數量k的變化曲線，其結果如圖3所示。

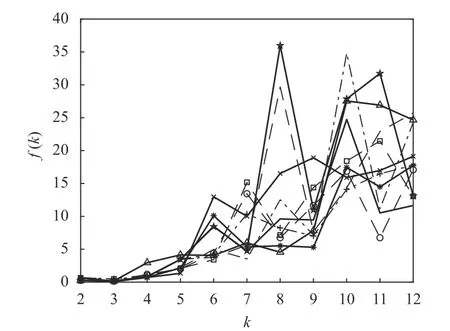
圖3 10 次運行中Iris 數據的f(k)隨k 變化的曲線

從圖3 可以看出，雖然K-均值算法的10 次運行結果各不相同，但在每次運行中，聚類有效性評價函數f(k)的最小值都是在k=3 時取得的，這是不變的。圖3 的結果說明f(k)對于確定最佳聚類數量是有效的。

在多次運行K-均值算法的基礎上，再考慮聚類有效性評價函數f(k)的平均性能。對于每個可能的k值，將10 次運行的f(k)求平均值可得到E[f(k)]，其結果如表4 和圖4 所示。可以看出，聚類有效性評價函數f(k)在K-均值算法10 次運行中的平均值E[f(k)]仍然在k=3 時取得最小值，這也反映了Iris 數據集中真實的鳶尾花品種為k=3。另外，由于K-均值算法對數據采用隨機的初始劃分，使得每次運行獲得的聚類中心位置并不相同，但從多次運行的結果來看，E[f(k)]仍然能夠準確地反映Iris 數據集的本質結構。即聚類有效性評價函數對K-均值的隨機初始化具有魯棒性(robustness)。

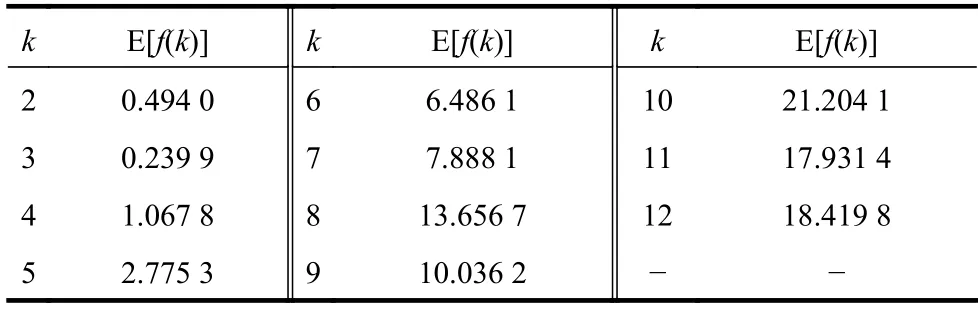
表4 Iris 數據的E[f(k)]值與k 的對應表

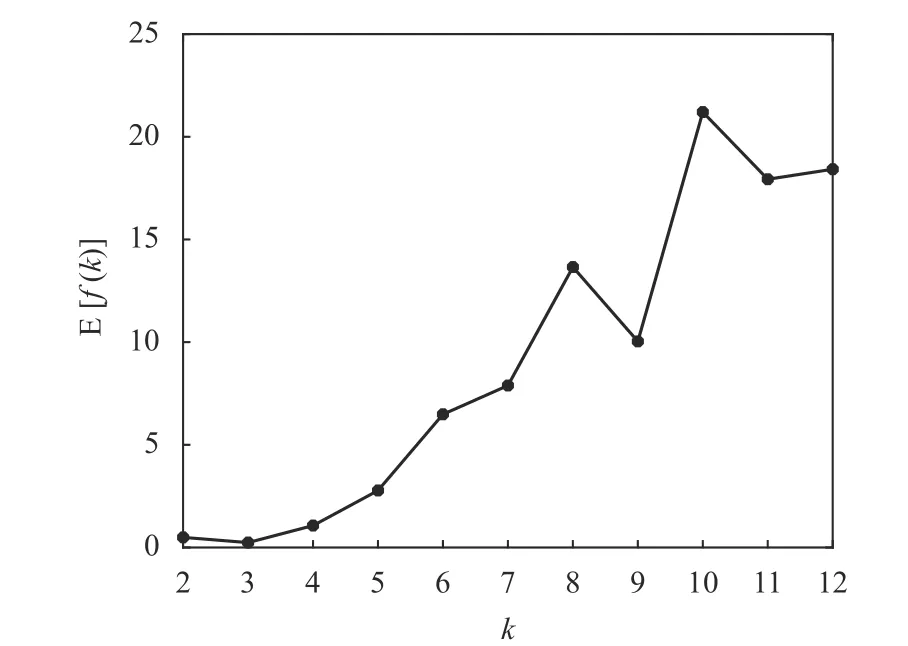
圖4 10 次運行中Iris 數據的E[f(k)]隨k 變化的曲線

3.2 數據集Seeds 的仿真

種子(Seeds)數據包括3 種小麥粒(wheat kernels)的7 個幾何參數(屬性)：面積(area)x1、周長(perimeter)x2、密度(compactness)x3、長度(length)x4、寬度(width)x5、不對稱系數(asymmetry coefficient)x6、溝槽長度(length of kernel groove)x7。顯然，這些屬性的度量單位是不相同的。Seeds 數據集對每一類小麥分別記錄了70 組特征的數據，按照類標簽1、2、3 的順序存放。

對于Seeds 數據，分別計算3 類(class 1, 2,3)小 麥7 個 屬 性x1,x2, ···,x7的 均 值，如 圖5 所示。以上均值給出的是3 類小麥所有樣本幾何參數的分布中心。根據數據集的樣本數量以及經驗規(guī)則，設Seeds 數據集中可能的聚類數量范圍為[kmin,kmax]，其中kmin=2，kmax=13。對于[kmin,kmax]中的每個k值，運行K-均值算法一次，并計算出相對應的聚類有效性評價函數f(k)，其結果如圖6所示。

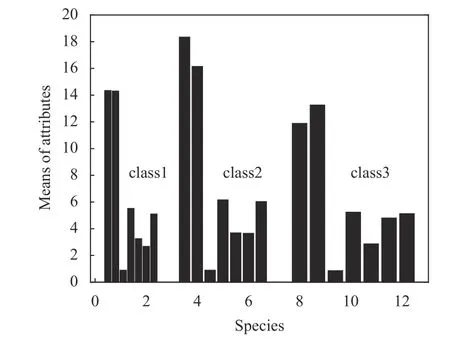
圖5 3 種小麥特征變量均值的條形圖

由聚類有效性評價函數(指標)的定義可知，若所有數據都屬于同一類(即k=1)，則指標f(k)=1。為了便于觀察和比較，在圖6 中還給出了k=1 的波形。可以看出，當k=3 時，聚類有效性評價指標f(k)取得一個最小值0.327 1，即給出了K-均值算法的最佳聚類數量為3。這一結果與Seeds 數據集的實際情況是一致的。

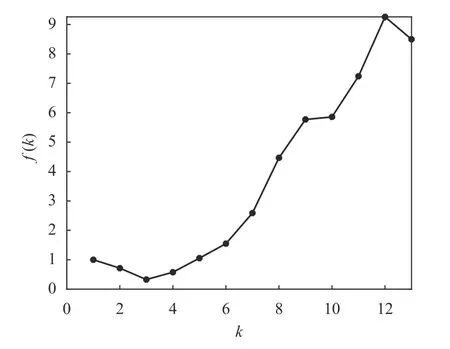
圖6 Seeds 數據的f(k)隨聚類數量k 的變化曲線

同樣地，為了考察K-均值算法在重復多次運行情況下的整體性能。對于Seeds 數據集，在k的可能取值范圍[kmin,kmax]內重復運行K-均值算法15 次，每次運行記錄和保存聚類有效性評價函數f(k)的對應值，其結果如圖7 所示。可以看到，在K-means 算法的15 次運行中，盡管每次運行f(k)的取值以及取值的分布情況都不相同，但是指標f(k)的最小值毫無例外地在k=3 時獲得。這表明聚類有效性評價函數f(k)在確定最優(yōu)聚類數量方面的性能是非常穩(wěn)定的。

對于每個可能的k值，把上述15 次K-均值算法運行所得到的f(k)值取平均得到E[f(k)]，繪制出E[f(k)]隨k值變化的曲線如圖8 所示。

由圖8 可以看出，從聚類有效性評價函數的平均性能E[f(k)]仍然可以清晰地識別出Seeds 數據集的真實聚類結構(k=3)。另外，從圖7 和圖8 的結果可知，在最優(yōu)聚類數量的確定方面，指標f(k)以及其平均值E[f(k)]的性能不會受到K-均值算法隨機初始化的影響。

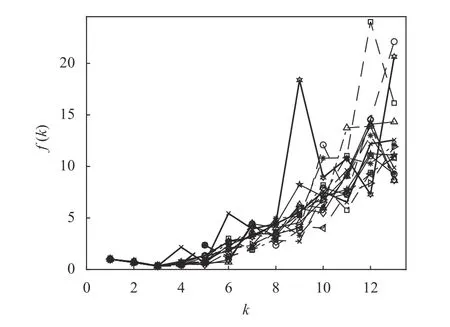
圖7 15 次運行中Seeds 數據的f(k)隨k 變化的曲線

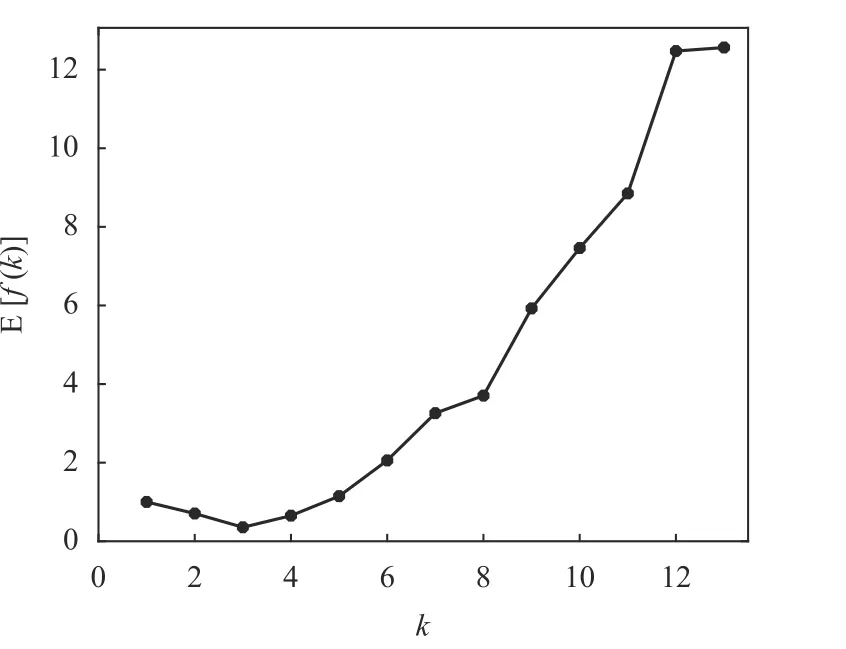
圖8 15 次運行中Seeds 數據的E[f(k)]隨k 變化的曲線

3.3 數據集Wine 的仿真

葡萄酒(Wine)數據是對在意大利同一地區(qū)種植，但來自3 個不同品種的葡萄酒進行化學分析的結果。這種分析確定了3 種類型的葡萄酒中所含13 種成分(屬性、特征)的含量。這些屬性分別為酒精(x1)、蘋果酸(x2)、灰(x3)、灰分堿度(x4)、鎂(x5)、總酚(x6)、黃酮素類化合物(x7)、非黃酮類酚類(x8)、原花青素(x9)、顏色強度(x10)、色調(x11)、稀釋葡萄酒的OD280/OD315(x12)和脯氨酸(x13)。這些特征值的度量單位是不相同的。Wine數據集中共記錄了178 組數據，3 種類型葡萄酒的類標簽分別為1, 2, 3，它們各自的樣本數分別為59, 71, 48。對于Wine 數據集，由于不同屬性(變量)的取值之間差距太大(相差3 720 倍)，無法用圖形表示變量的均值。這里僅給出全部13 個變量的平均值(包括所有葡萄酒的種類)，其結果如表5所示。

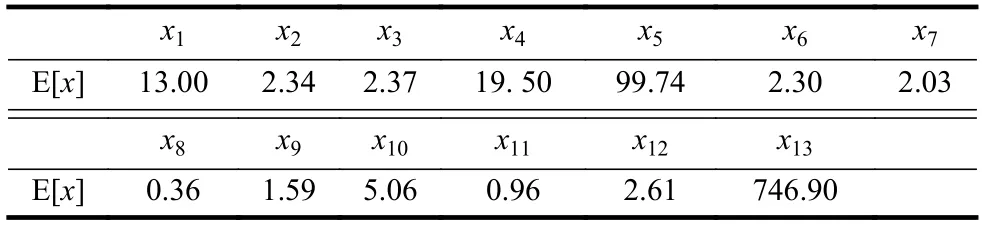
表5 Wine(全部種類)數據各屬性的平均值

Wine 數據的均值給出了各屬性值分布的大致統計中心。考慮到Wine 數據集的屬性較多，根據經驗規(guī)則將數據可能的聚類數量設置為kmin=2,kmax=16。首先對于區(qū)間[kmin,kmax]中的每個k值，運行K-均值算法一次，并計算出相對應的聚類有效性評價函數f(k)的值，其結果如表6 和圖9 所示。

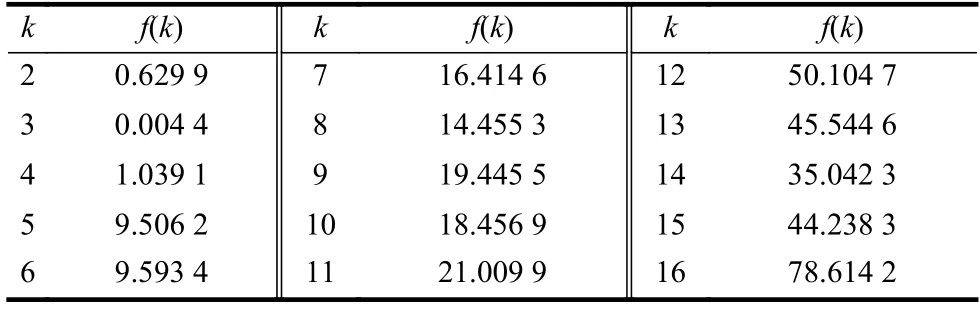
表6 Wine 數據的f(k)與k 的對應表

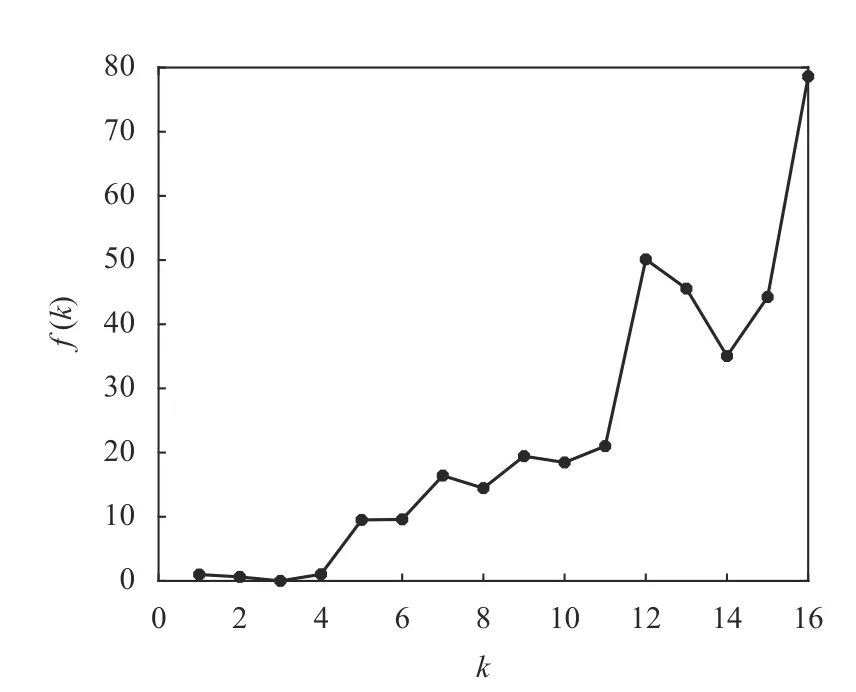
圖9 Wine 數據的f(k)隨聚類數量k 的變化曲線

為觀察方便，圖9 也給出了k=1 對應的數據。由于f(k)取值的范圍較大，最小值附近其差別不易區(qū)分，為此把圖9 中的數據列在表6 中。從表6 中的數據可知，f(2)是f(3)的143 倍，f(4)是f(3)的236 倍。顯然，k=3 是指標f(k)的最小值點，即k=3 是最優(yōu)的聚類數量，這與Wine 數據本質結構是一致的。

類似地，對于Wine 數據集，在可能的聚類數量范圍[kmin,kmax]內重復運行K-均值算法15 次，計算并記錄每次運行中指標f(k)的取值，其結果如圖10 所示。

從圖10 也可看出，在運行K-均值算法的過程中，由于指標f(k)的取值范圍較大，在它的最小值點附近的指標f(k)取值也不易區(qū)分。為此，考慮15 次運行K-均值算法得到的平均性能E[f(k)]，其結果如圖11所示。

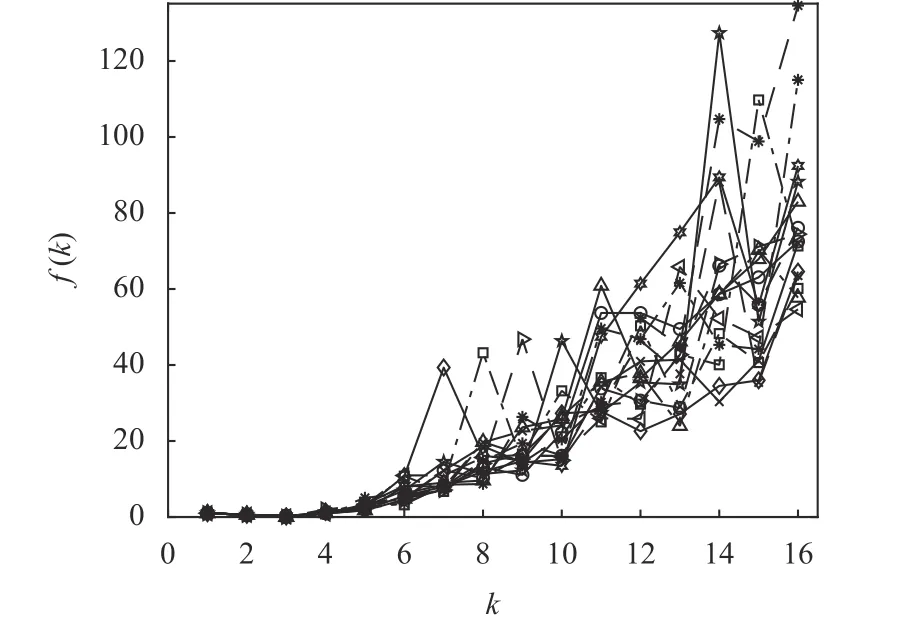
圖10 15 次運行中Wine 數據的f(k)隨k 變化的曲線

從圖11 可以看出，對于Wine 數據，隨著聚類數量k值的增加，指標的平均值E[f(k)]曲線變化的大致趨勢是：當k＜3 時，E[f(k)]曲線是遞減的；當k＞3 時，E[f(k)]曲線是遞增的，因此在k=3 時取得E[f(k)]的最小值。為了更清楚地比較在E[f(k)]最小值附近數值上的差別，將圖11 中的E[f(k)]值列在表7 中。可以看出，E[f(2)]大約是E[f(3)]的3.65 倍，而E[f(4)]大約是E[f(3)]的6.8 倍。

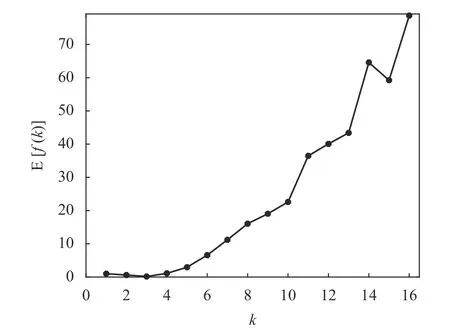
圖11 15 次運行中Wine 數據的E[f(k)]隨k 變化的曲線

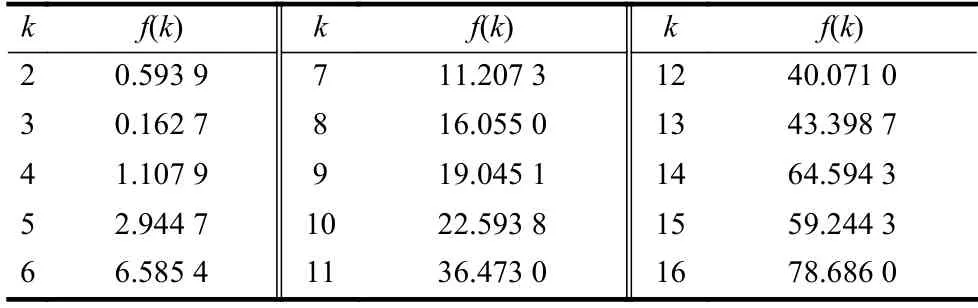
表7 Wine 數據的E[f(k)]值與k 的對應表

盡管Wine 數據集的平均性能E[f(k)]的取值范圍相當大，但從它的全局極小值即最小值來說，仍然能辨別出k=3 是Wine 數據集最優(yōu)的聚類數量。

從以上對3 個UCI 數據集(Iris, Seeds, Wine)的仿真結果可知，利用聚類有效性評價函數f(k)，不僅能夠對原始數據集提供最優(yōu)的聚類數量，而且從多次重復運行K-均值算法的效果來看，函數f(k)還能夠對隨機初始化提供很強的魯棒性。

4 結 束 語

為了克服K-均值聚類算法需要用戶預先指定聚類數量的缺陷，本文對K-均值算法的基本迭代步驟和聚類有效性進行了分析；然后，基于數據點的歐幾里得距離，給出了類間質心距離之和、類內距離之和的定義，用于度量不同聚類間和同一聚類的數據距離；最后，提出了一種由類間質心距離之和與類內距離之和構造而成的聚類有效性評價函數，用以確定數據最優(yōu)的聚類數量。在數據可能的聚類數量范圍內，利用求解聚類有效性評價函數的最小值來確定K-均值算法的最佳聚類數量。通過對UCI 中Iris、Seeds 和Wine 數據集的仿真，證明了所提出的聚類有效性評價函數不僅能夠準確地反映原始數據的真實聚類結構，而且還能有效地降低K-均值算法對隨機初始化的敏感性。