適用于中點鉗位H橋五電平逆變器的快速SVPWM算法

吳宇濤， 賈何飛， 鄧焰

(浙江大學 電氣工程學院，浙江 杭州 310027)

0 引 言

多電平逆變器具有輸出電壓等級高、單個功率器件承受電壓應力小、開關損耗小、輸出電壓諧波含量低等優勢，在中高壓大功率領域的應用備受學者青睞[1-5]。

目前主流的多電平逆變器的拓撲有：中點鉗位型(neutral point clamped,NPC)、飛跨電容型(flying capacitor,FC)、級聯H橋型(cascaded H-bridge,CHB)以及立足于上述拓撲的混合改進型[6-7]。多電平逆變器輸出性能的重要影響因素是其采用的調制技術。當下普遍應用的調制技術包括：正弦脈寬調制(sinusoidal PWM,SPWM)技術[8-10]、選擇性消諧波脈寬調制(selective harmonic eliminate PWM, SHEPWM)技術[11]以及空間矢量脈寬調制(space vector PWM,SVPWM)技術[12-20]。SPWM技術算法簡單、計算量小，但缺陷是直流電壓利用率低，線性調制區的最大直流電壓利用率僅為0.707。SHEPWM技術的優勢是能夠消除給定次數的諧波。然而，該技術若在線運算，則需求解非線性超越方程組，計算量龐大；若預先儲存開關角，則控制靈活性降低。SVPWM技術具有概念清晰，直流電壓利用率高的特點[19]。線性調制區的最大直流電壓利用率比SPWM提升了15%。綜上所述，在某些多電平逆變器的調制領域，SVPWM技術具有顯著優勢[20]。

多電平SVPWM技術的復雜度高于兩電平SVPWM技術，且電平數越高，算法復雜度越高。這是因為多電平SVPWM技術的電壓矢量數目與電平數呈三次方關系，扇區內小三角形數目與電平數呈平方關系[21]。因此，多電平SVPWM技術的簡化受到學術界的廣泛關注[12-18]。文獻[12]以直角坐標系為基礎，提出了一種拉伸坐標系。基于拉伸坐標系的算法雖然消除了根號運算，但無法避免正弦運算。文獻[13]立足于坐標變換方法，提出了開關序列映射SVPWM技術。該技術通過坐標變換判斷參考矢量的位置，通過映射表安排開關序列。然而，該方法的不足之處是在五電平及更高電平數領域，開關序列大幅增加，映射表內容隨之擴充且映射時間也顯著增加。文獻[14]提出了一種將多電平SVPWM簡化為三電平SVPWM，并利用扇區旋轉對稱的特點進一步減小計算量的技術。不過簡化后的三電平SVPWM計算過程仍然比較復雜，包含了大量正弦運算。文獻[15-16]分別針對級聯型拓撲和一種新型五電平拓撲，提出了簡化多電平SVPWM技術，但是這兩種算法對其他多電平拓撲的通用性不強。文獻[17-18]的簡化思路是將三電平SVPWM分解為兩電平SVPWM。這兩種方案都只能局限于三電平逆變器，因為分解出的兩電平空間矢量圖的位置隨參考矢量的移動而變化，在電平數更多的場合，這兩種算法的計算量依然較大。

為簡化五電平SVPWM技術算法，提出一種適用于五電平逆變器的快速SVPWM算法。首先，分析傳統五電平SVPWM算法的原理，得出傳統算法復雜度高的本質原因。其次，在分析五電平空間矢量圖的基礎上，提出一種扇區分割方案，將五電平空間矢量圖分割為若干個位置固定的兩電平空間矢量圖，應用兩電平SVPWM的參考矢量位置判斷和基本矢量作用時間計算的方法，從而將五電平SVPWM簡化為兩電平SVPWM，實現運算量的減小。最后，實驗驗證新算法的可行性和快速性。

1 傳統五電平SVPWM算法

傳統五電平SVPWM算法(以下簡稱為傳統算法)由兩電平SVPWM算法推廣而得。五電平空間矢量圖如圖1所示。

圖1 五電平空間矢量圖

設逆變器直流母線電壓為Vdc。圖中的數字0～4分別對應五電平逆變器每相可以輸出的5種電平“Vdc、Vdc/2、0、-Vdc/2和-Vdc”，因此三相五電平逆變器共計可以輸出53=125個電壓矢量，不過由于存在作用效果相同的電壓矢量，因此，只有61種不同位置的電壓矢量，稱之為基本矢量。Vref是參考矢量，其幅值不變，在空間矢量圖中勻速旋轉。空間矢量圖被劃分為6個扇區，用羅馬數字Ⅰ至Ⅵ表示。每個扇區包含16個小三角形，用數字1～16表示。

傳統算法的實現過程一般分為3個步驟：確定參考矢量的位置、計算基本矢量的作用時間、安排開關序列。由于各個扇區旋轉對稱，因此只需分析扇區Ⅰ即可。首先應確定參考矢量Vref位于哪個小三角形中，傳統算法的判斷方法是建立直角坐標系，求出坐標系中每個小三角形邊界的表達式。通過邊界條件法，判斷參考矢量位于16個小三角形的哪個小三角形中，如圖2所示。

圖2 傳統算法位置判斷

其次，根據伏秒平衡原理以及幾何關系，求出每個小三角形中基本矢量的作用時間公式。由于每個小三角形的位置都不相同，因此共有16組公式，且每組公式都包含正弦運算，如表1所示。最后，安排開關序列，產生驅動信號。

表1中：t0、t1和t2為基本矢量的作用時間；Ts是載波周期；A、B和C的表達式為：

表1 傳統算法基本矢量作用時間

式中θ是參考矢量與x軸的夾角，如圖2所示。

傳統算法雖然思路清晰，但計算量較大。原因有以下兩點：一是為判斷參考矢量的位置，最多需要應用16次邊界條件法；二是共有16組基本矢量作用時間的計算公式，且每組公式都包含正弦運算。對于微處理器而言，實現正弦運算需調用math函數，因此，所需時間遠遠超過加減乘除運算。

2 新型扇區分割方式

基于扇區分割的快速五電平SVPWM算法(以下簡稱為扇區分割算法)的3個基本步驟與傳統算法相同：第一步，確定參考矢量的位置；第二步，計算基本矢量的作用時間；第三步，安排開關序列。其中，第三步的原理與傳統算法完全相同，而第一步和第二步是扇區分割算法的主要簡化對象，簡化的思路是將五電平空間矢量圖分割為若干個兩電平空間矢量圖。在此基礎上，首先判斷參考矢量位于哪個兩電平空間矢量圖中。其次，運用兩電平SVPWM算法判斷參考矢量所處位置，并計算基本矢量的作用時間。

多電平空間矢量圖的扇區是旋轉對稱的。換言之，可以通過單個扇區的旋轉對稱，得到完整的空間矢量圖。由此可以得到區別于傳統扇區設計方式的另一種設計方式，如圖3所示，稱之為四邊形扇區設計方式。

圖3 四邊形扇區設計方式

以四邊形扇區設計方式為基礎，將每個扇區分割為若干個完整或不完整的兩電平空間矢量圖。然而，扇區分割的方案具有不唯一性。以扇區Ⅰ為例，扇區分割的示意圖如圖4所示。

圖4 扇區分割示意圖

可以看出，圖4所示的兩種分割方法分別將扇區分割成了6個區域和7個區域。為了減少在判斷參考矢量位于哪個區域的步驟中的計算量，分割出的區域數目應盡量少。因此，以扇區Ⅰ為例，本文提出了一種四區域分割方案，如圖5所示。這4個區域用字母A到D表示，區域的中心點用字母a～d表示。每個區域都不是完整的兩電平空間矢量圖，4個區域緊密貼合，共同組成了一個完整的扇區。各區域的邊界表達式將在后文給出。

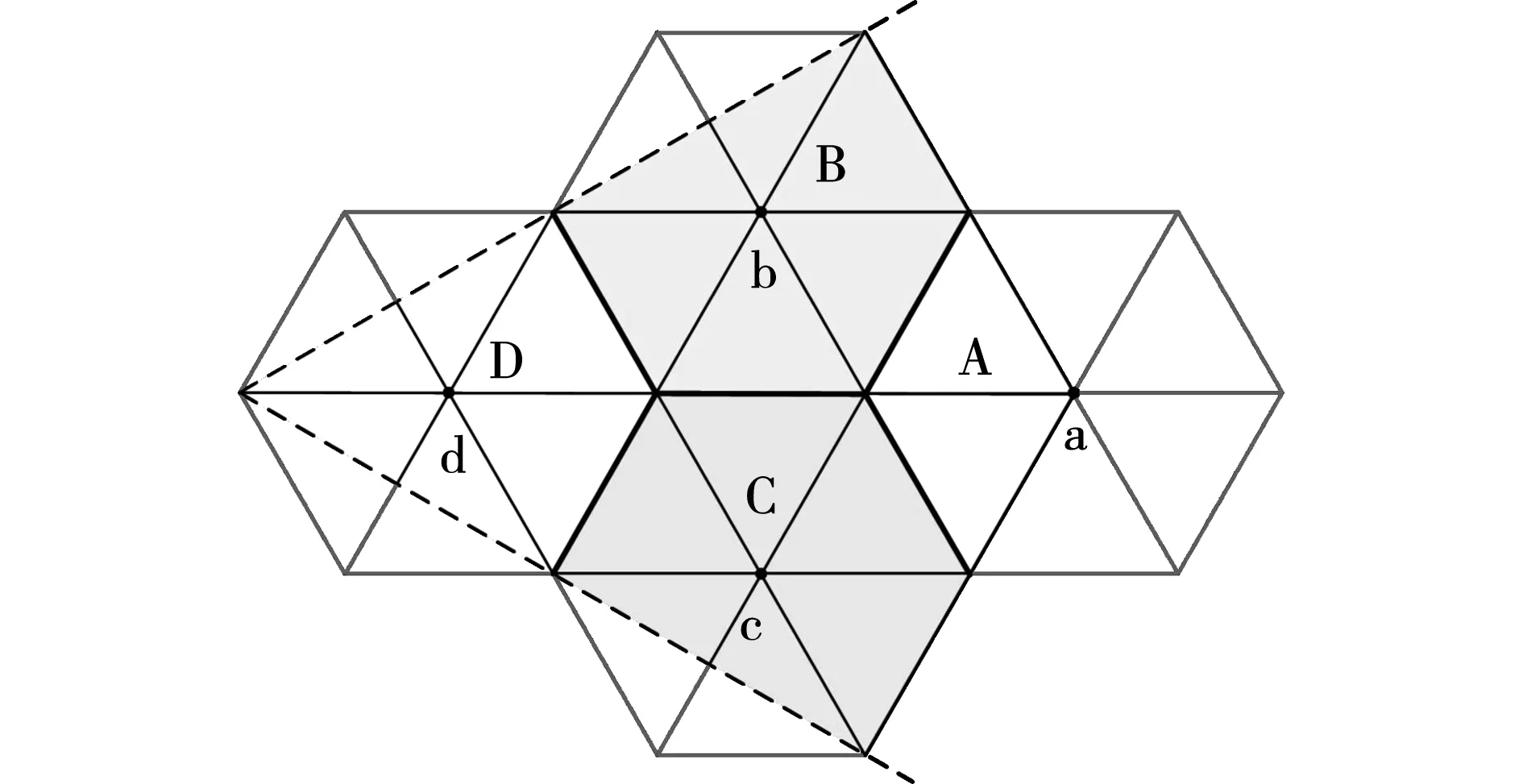
圖5 扇區的分割方案

至此，通過重新設計并分割扇區，實現了將五電平空間矢量圖等效為4個兩電平空間矢量圖組合的目標。

3 扇區分割算法

接下來將依據上文提出的扇區分割方案，詳細闡述扇區分割算法的原理。

以零矢量為原點，扇區Ⅰ的角平分線為x軸，建立直角坐標系，如圖6所示。

圖6 新算法位置判斷

參考矢量Vref的坐標是(Vx,Vy)。圖6中各區域的邊界對應的直線表達式如表2所示。根據邊界條件法，即可判斷參考電壓在A、B、C或D哪個區域中。判斷條件如表3所示。

表2 邊界表達式

表3 區域判斷

以參考矢量Vref所在區域的中心點坐標(即圖6中的a、b、c或d點)為基準，修改Vref的坐標(Vx,Vy)，修改后的新參考矢量Vrefm的坐標為(Vxm,Vym)，其表達式為：

如圖6所示，以A區為例，β為新參考矢量Vrefm的角度，則有

根據tanβ的大小和Vym的正負，即可判斷新參考矢量Vrefm位于哪一個小三角形中。

綜上可見，本文所提出的扇區分割算法最多只需應用4次邊界條件法，就可以判斷出參考矢量的位置。然而，傳統算法需應用至多16次邊界條件法。相較于傳統算法，新算法的計算量顯著減少。

確定參考矢量所在小三角形的目的是以小三角形頂點所在的3個基本矢量來合成參考矢量。3個基本矢量的作用時間分別記為t0，t1和t2。由圖1可見，所有的小三角形都可以被分為兩類，正三角形和倒三角形。t0、t1以及t2與小三角形頂點的基本矢量的對應關系如圖7所示。

圖7 兩類小三角形

兩電平空間矢量圖如圖8所示。運用兩電平SVPWM的基本矢量作用時間公式(如表4所示)，即可計算出基本矢量的作用時間。

圖8 兩電平空間矢量圖

表4 扇區分割算法基本矢量作用時間

表中：Ts是載波周期；k、p和q的表達式分別為：

對比表1和表4可見，本文所提出的扇區分割算法的基本矢量作用時間公式僅有6組，且每組公式都只含加減乘除運算，不含正弦運算，而傳統算法共有16組基本矢量作用時間公式，且每組公式都包含正弦運算。

4 實驗驗證

為驗證扇區分割算法的正確性和快速性，搭建了一臺三相NPC/H橋五電平逆變器樣機。樣機實拍圖如圖9所示。樣機的電路拓撲如圖10所示。

圖9 逆變器樣機

圖10 逆變器拓撲

圖10中直流源V1、V2和V3互相隔離且輸出電壓都為Vdc。NPC/H橋五電平逆變器一共有24個開關管，因此需要24路獨立的PWM控制信號。然而，DSP芯片最多只能提供12個獨立的PWM輸出口。為解決這一矛盾，樣機控制器采用雙層控制結構。上層芯片為STM32F429，其任務是運行調制程序，并將計算結果發送給下層芯片。下層芯片為兩個TMS320F28069型號的DSP芯片，其任務是接收上層芯片的計算結果，產生PWM脈沖信號。其中一個DSP控制A相和B相功率板，另一個DSP控制C相功率板。上下兩層芯片之間的通信通過光纖完成。

樣機采用的IGBT型號為IHW30N160R5，驅動光耦為UCC5310MCDR，負載為三相對稱星型電阻負載。樣機的實驗參數如表5所示。實驗結果如圖11和圖12所示。

表5 實驗參數

為了驗證所提方法的有效性和優越性，在直流母線電壓為150 V、參考矢量幅值為170 V的工況下，對傳統算法和本文所提的扇區分割算法進行實驗比較。

圖11(a)和圖12(a)是輸出電壓波形圖，從圖可以看出，傳統算法和扇區分割算法的輸出電壓波形幾乎相同。圖11(b)和圖12(b)是輸出電壓頻譜圖，從圖可以看出，兩種方法的輸出線電壓幅值非常接近，分別為292.70 V和292.62 V，近似等于理論值294.45 V。總諧波畸變率(total harmonic distortion，THD)同樣非常接近，都為0.79%(本文中總諧波畸變率計算到50次)，諧波含量非常低。

圖11 傳統算法實驗結果

圖12 扇區分割算法實驗結果

綜上所述，就輸出電壓波形和基波諧波性能而言，本文所提的扇區分割算法具有和傳統算法同樣優越的性能。這是因為扇區分割算法的底層原理與傳統算法相同，只是計算過程不同。

為驗證本文所提的扇區分割算法的快速性，在樣機上開展了程序耗時對比測試實驗。如前文所述，傳統算法和扇區分割算法都分為判斷參考矢量位置(以下簡稱為步驟一)、計算基本矢量的作用時間(以下簡稱為步驟二)以及安排開關序列(以下簡稱為步驟三)3個步驟。為保證程序耗時對比的準確性，兩者的程序都按統一的框架，即上述3個步驟編寫。兩種算法程序的編寫思路如圖13所示。分別針對傳統算法和扇區分割算法，在不同調制度下各做100次實驗，求出各部分程序的平均耗時。以傳統算法的總耗時為基準，歸算程序的耗時數值，如表6和圖14所示。

圖14 程序各部分耗時歸一化對比

表6 程序各部分耗時歸一化對比

圖13 兩種算法的程序流程圖

對各部分而言，扇區分割算法的步驟一耗時相較于傳統算法有所縮短。這是因為傳統算法在步驟一中最多需應用16次邊界條件法才能判斷出參考矢量的位置，而扇區分割算法至多只需4次邊界條件法；扇區分割算法的步驟二耗時相較于傳統算法大幅縮短。這是因為傳統算法計算基本矢量作用時間的公式中包含正弦運算，而扇區分割算法僅包含簡單的加減乘除運算；兩種算法的步驟三耗時近似相等，因為三者的安排開關序列的算法完全相同。 就整體而言，扇區分割算法的耗時為傳統算法的55.27%，運算時間大幅縮短。

5 結 論

本文針對傳統五電平SVPWM算法計算量大的問題，提出了一種基于扇區分割的快速五電平SVPWM算法。實驗驗證了新算法的可行性和快速性。本文所提出的新算法具有以下優勢：

1)就程序的運算速度而言，新算法的程序運行耗時為傳統算法算法的55.27%，運算速度相較于傳統算法大幅提升。

2)新算法在簡化運算，減小計算量的基礎上，保持了與傳統算法同樣優越的的輸出電壓的基波和諧波性能。