特殊環境下雙饋風力發電機電刷磨損量建模

趙帥， 馬宏忠， 程龍

(河海大學 能源與電氣學院，江蘇 南京 210098)

0 引 言

電刷滑環作為雙饋電機靜止和運動部件之間電能轉換的重要部件，其本身的運行特性極其復雜，電刷損耗快，需定期更換，其工作性能極易受環境影響[1]。在復雜的海洋環境下，鹽霧沉積影響電刷滑環接觸面的摩擦系數，電刷的磨損量增大，電刷更換周期縮短，預測電刷的磨損量具有一定現實意義[2]。

當前國內外學者對電刷的磨損已經取得一些成果。文獻[3]通過對單極發電機電刷滑環系統機械環境測試，研究了大電流密度下陽極刷和陰極刷的接觸電阻，并對兩極電刷不同的磨損率進行量化，發現陽極刷的磨損率是陰極刷的兩倍。文獻[4]從摩擦學出發，建立電刷滑環系統的磨損過程曲線，在環境變化時，會出現過渡期，并且可以觀察到多個穩定磨損階段。文獻[5]通過威布爾分布的統計分析評估電刷滑環的使用壽命以及最優的定期檢測方案，減少不必要的維修計劃，增加了系統的可靠性。文獻[6]研究了石墨碳刷與鋼滑環和銅滑環之間的電壓-電流特性，研究表明鋼滑環的電壓飽和特性與銅滑環的電壓飽和特性有很大不同。文獻[7]研究了電刷滑環系統中不同銀含量的電刷在特定工況下的接觸壓降以及磨損情況，實驗表明，銀含量在60%～80%之間，電刷的接觸壓降以及磨損性能比較好，不同銀含量的電刷在相同的工況下，電氣磨損及機械磨損的占比有所不同。文獻[8]研究了實際工況中以及實驗室條件下電刷滑環系統在不同的電流密度下的磨損率，研究發現電刷滑環運行期間勵磁電流在并聯的電刷之間分布不均。電接觸過程中摩擦模型建模也取得了一些成果，文獻[9]提出一種能夠準確描述運動狀態下的摩擦力模型；文獻[10-11]通過引進Stribeck函數建立改進的摩擦力模型；文獻[12]提出了兼具靜摩擦和庫侖摩擦基本摩擦特性的改進的Dahl模型；文獻[13-14]從波動載荷出發，研究波動載荷與滑動電接觸摩擦力之間的關系，建立關于波動載荷下的滑動電接觸摩擦力模型。以上研究分別研究了電刷滑環系統的磨損特性以及電接觸下摩擦力建模，但未將摩擦力模型和磨損量預測結合，未涉及海洋環境下電刷磨損量預測研究。

隨著雙饋電機在海洋風電上的發展，針對電刷滑環系統故障診斷上取得突出成就，文獻[15-17]基于振動信號提取，提出合理的滑環燒蝕故障診斷方法，但針對電刷滑環的研究仍有很多問題，如海洋環境下電刷磨損加劇更換周期難以確定等。基于文獻[18]中海洋環境下鹽霧對風電機組的影響以及文獻[19]中對鋁合金在鹽霧環境中的腐蝕機理的分析，為研究海洋環境下電刷滑動電接觸下的磨損量，設計了基于鹽霧試驗機的雙饋電機電刷滑環系統磨損量研究實驗平臺，采用改進的庫倫-粘性摩擦力模型，結合磨損理論，建立電刷的磨損量預測模型，然后，基于粒子群算法，對磨損量模型中接觸電流、接觸壓力、鹽霧濃度、運行速度以及實驗溫度相關的參數進行辨識，建立能夠預測不同接觸電流、接觸壓力、鹽霧濃度、運行速度以及實驗溫度工作條件下電刷的磨損量預測模型，并利用實驗數據驗證該模型的可靠有效。

1 實驗裝置與實驗方案

1.1 實驗裝置

圖1是基于鹽霧試驗機的電刷滑環系統磨損試驗平臺，主要包括鹽霧試驗箱、異步電機、變頻器、調壓器、電網系統、電刷滑環系統以及傳感器等實驗設備。鹽霧試驗箱可以改變實驗環境，通過配置1%～5%NaCl溶液，實現腐蝕環境的改變；異步電機和變頻器的結合實現電刷滑環系統在0～1 500 r/min轉速范圍內變化；調壓器可以改變電刷的加載電流，創造出不同的工況條件；傳感器可以實現設備的檢測和保護。

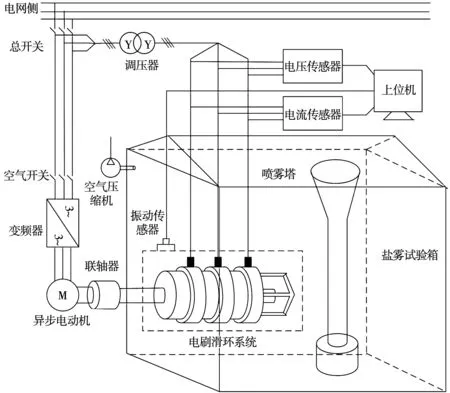
圖1 基于鹽霧試驗機的電刷滑環系統磨損試驗平臺

實驗中的電刷滑環系統為YKYF1500-4異步空冷雙饋式風力發電機電刷滑環系統。碳刷種類繁多，可選擇性較廣，不同材質的碳刷磨損性能不同，選取Cu含量為10%的碳刷作為研究對象，尺寸如表1所示。

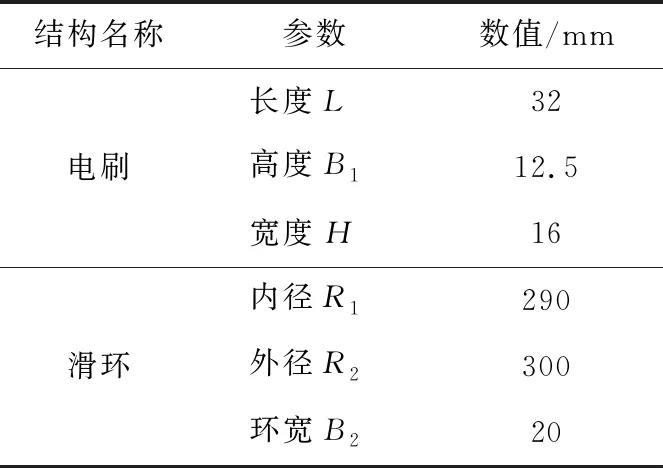
表1 電刷滑環的結構參數

1.2 實驗方案

基于控制變量法，進行接觸電流、接觸壓力、鹽霧濃度、溫度與滑動速度實驗，共計64組實驗，每組實驗6 h，每組實驗后用0.1 mg精確度的電子天秤測量電刷在該實驗時間內的磨損量。根據電刷滑環的工況條件以及鹽霧試驗箱的相關實驗標準，將實驗條件確定為：轉動速度為300、600、900、1 200 r/min；電流大小為10、20、30、40 A；壓力大小為：15、20、25、30；鹽霧濃度為1%、3%、5%、7%；實驗環境溫度為32、35、38、41 ℃。每次實驗后對電刷進行沖洗、烘干和稱重，減少鹽霧試驗箱中鹽霧沉積及水汽對實驗結果的影響。

圖2為金相顯微鏡下電刷磨損前后形貌對比。由圖2(a)知，磨損前的電刷表面比較光滑，磨損后，由于電刷與滑環之間滑動摩擦，電刷表面會有較明顯的擦痕，另外由于鹽霧沉積等腐蝕環境的影響，電刷表面會有較明顯的點蝕坑，由載流腐蝕與鹽霧腐蝕共同作用形成，如圖2(b)所示。由以上分析可知，海洋環境下，電刷的磨損由機械磨損和電氣磨損共同決定。

電刷滑環系統高速運轉，滑環表面溫度升高，高溫環境下銅與氧氣結合形成氧化膜，其反應式子如下：

(1)

(2)

一般情況下氧化膜的形成具有一定的潤滑作用，減少電刷磨損。海洋環境下，暴漏在空氣中的電刷滑環表面會被一層水膜覆蓋，在電場作用下會被電解，游離出氫氧根離子和氫離子，即

(3)

鹽霧沉積至使電刷滑環表面形成NaCl顆粒，溶于水后析出鈉離子和氯離子，在水和氧的共同作用下，產生電化學腐蝕，形成腐蝕坑。其反應式子[20]如下：

(4)

(5)

由反應式子可知，海洋環境下，受環境影響，電刷工作性能改變，鹽霧腐蝕造成電刷磨損加劇。

2 磨損模型的建立

2.1 摩擦力模型

1)傳統庫倫-粘性摩擦力模型。

隨著流體力學的發展，用庫倫-粘性模型來表征滑動摩擦力F(v)，該摩擦模型是由粘性模型和庫倫模型結合而成，可以表示[21]為

F(v)=Fc+fvvsgn(v)。

(6)

式中：Fc為庫侖摩擦力；fv為粘性摩擦系數。

庫倫-粘性摩擦模型的摩擦力與速度的關系如圖3所示。由圖可知，摩擦力隨速度增大而增大，此模型中摩擦力與速度呈簡單的線性關系。實際上，摩擦力與速度之間非簡單的線性關系。

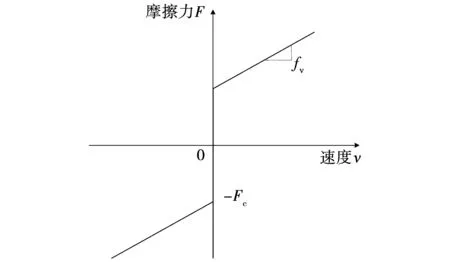
圖3 庫倫-粘性摩擦模型

2)改進庫倫-粘性摩擦力模型。

由庫倫定理知，庫侖摩擦力Fc與速度沒有關系，對式(6)庫倫-粘性模型中的粘性部分改寫，即將式(6)中fvvsgn(v)改寫為

Fv=σv1(eσv2|v|-1)sgn(v)。

(7)

將式(7)代入式(6)，摩擦力與相對滑動速度之間的非線性的庫倫-粘性摩擦力模型[13]為

F(v)=Fc+σv1(eσv2|v|-1)sgn(v)。

(8)

式中：σv1為粘性摩擦斜率因子；σv2為粘性摩擦變化因子。從式(8)中可知摩擦力隨速度非線性變化，能更好地反映滑動速度與滑動摩擦力之間的關系。

2.2 磨損量建模

根據磨損理論，用單位摩擦功的體積磨損量來衡量磨損能量與磨損量之間的關系，電刷滑環系統中電刷的磨損量可表示[22]為

M=qW。

(9)

式中：M為體積磨損量；q為能量磨損率；W為摩擦功。

式(9)表示了體積磨損量M和摩擦功W之間的關系，摩擦功可表示為

W=F(v)vt。

(10)

式中F(v)為接觸摩擦力。

實驗中，電刷磨損之后測量質量比較直觀簡潔，式(9)改寫為

Ma=Mρ=ρqF(v)vt。

(11)

式中：Ma表示時間t內電刷的磨損量；ρ為材料密度。

進一步將式(11)改寫為

(12)

其中Mb表示單位時間磨損量。從式(12)中可看出：電刷單位時間磨損量與物質本身的密度ρ；能量磨碎損率q；以及運行速度v和接觸摩擦力F(v)相關。其中密度ρ和能量磨損率q是電刷材料的性質，通過查閱材料手冊或者簡易實驗很容易得。速度v和接觸摩擦力F(v)與電刷的具體運行工況相關，不同的工況下取值不同。將式(8)代入式(12)可得電刷的單位時間磨損量為

Mb=ρqv(Fc+σv1(eσv2|v|-1)sgn(v))。

(13)

可見，電刷單位時間磨損量由電刷的密度ρ、能量磨損率q、運行速度v、庫侖摩擦力Fc、粘性摩擦斜率因子σv1、粘性摩擦變化因子σv2確定。

2.3 反映相關變量的磨損量模型

在速度為v=300、600、900、1 200 r/min，接觸電流I=10、20、30、40 A，接觸壓力F=20 N，鹽霧濃度C=5%，實驗環境溫度T=35 ℃的實驗條件下，進行磨損量與接觸電流之間的關系實驗，實驗結果如圖4所示。隨著施加在電刷上的電流的增大，電刷的磨損量先減小后增大。

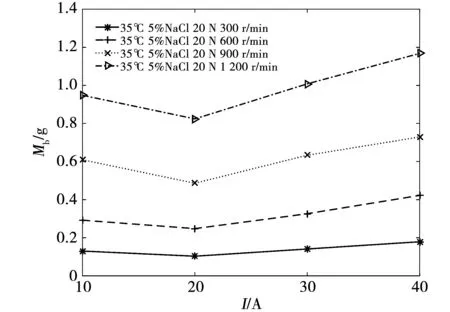
圖4 磨損量與接觸電流的關系

在速度為v=300、600、900、1 200 r/min，接觸壓力F=15、20、25、30 N，接觸電流I=20 A，鹽霧濃度C=5%，實驗環境溫度T=35 ℃的實驗條件下，進行磨損量與接觸壓力之間的關系實驗，結果如圖5所示。結合磨損量的計算公式，磨損量隨著接觸壓力的增大而增大，這與圖5中的的實驗結果相一致。

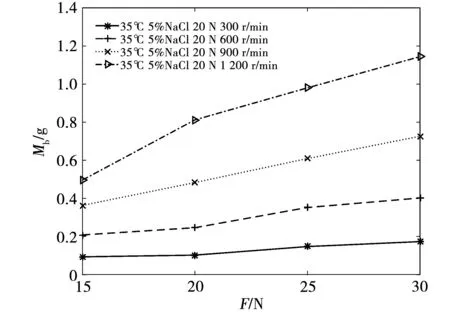
圖5 磨損量與接觸壓力的關系

在速度為v=300、600、900、1 200 r/min，接觸壓力F=20 N，接觸電流I=20 A，鹽霧濃度C=1%、3%、5%、7%，實驗環境溫度T=35 ℃的實驗條件下，進行試驗磨損量與鹽霧濃度之間的關系實驗，實驗結果如圖6所示。環境中NaCl濃度會對碳刷的磨損量造成一定的影響，契合了海洋環境下碳刷磨損加劇的現象。

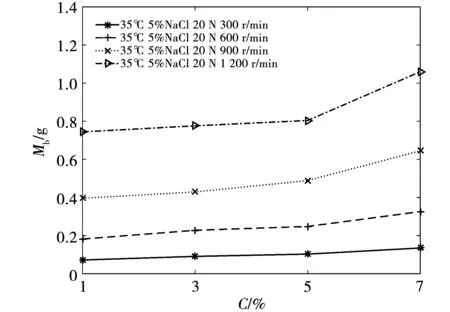
圖6 磨損量與鹽霧濃度的關系

在速度為v=300、600、900、1 200 r/min，接觸壓力F=20 N，接觸電流I=20 A，鹽霧濃度C=5%，實驗環境溫度T=32、35、38、41 ℃的實驗條件下，進行試驗磨損量與環境溫度之間的關系實驗，實驗結果如圖7所示。電刷滑環系統的溫度比環境溫度高，環境對電刷磨損性能的影響不如鹽霧濃度、電流及接觸壓力劇烈，該曲線增長平緩。

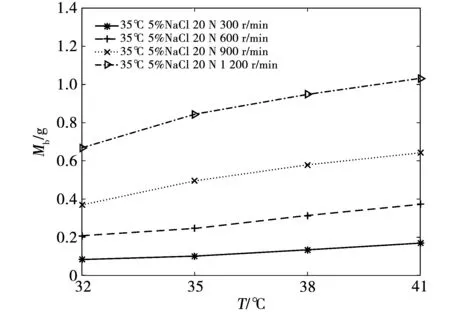
圖7 磨損量與環境溫度的關系

利用I、F、C、T分別表示接觸電流、接觸壓力、鹽霧濃度、環境溫度，基于庫倫-粘性摩擦力的磨損量模型可以改寫為：

(14)

式中Mb為改進模型的單位時間磨損量。

3 磨損量模型參數辨識

3.1 粒子群參數辨識

本文采用粒子群參數辨識方法對模型中Fc、σv1、σv2進行辨識，適應度函數定義[23]為：

(15)

e[Mb,Mbi]=Mb-Mbi。

(16)

式中：e[Mb,Mbi]為第i次磨損量的預測值與實驗值之間的誤差；Mbi為第i次磨損量的實驗值；N=4為試驗次數。

當I=10、20、30、40 A，F=20 N，C=5%，T=35 ℃；F=15、20、25、30 N，I=20 A，C=5%，T=35 ℃；F=20 N，I=20 A，C=1%、3%、5%、7%，T=35 ℃；F=20 N，I=20 A，C=5%，T=32、35、38、41 ℃時，分別用粒子群算法對基于改進的庫倫-粘性摩擦力的磨損量模型中的參數進行辨識。其中：參數為sizpop=60；maxgen=600；學習因子C1=2，C2=2；慣性權重ω=0.7；搜索空間維數D=3。對Fc、σv1、σv2進行最優辨識，結果如表2所示。

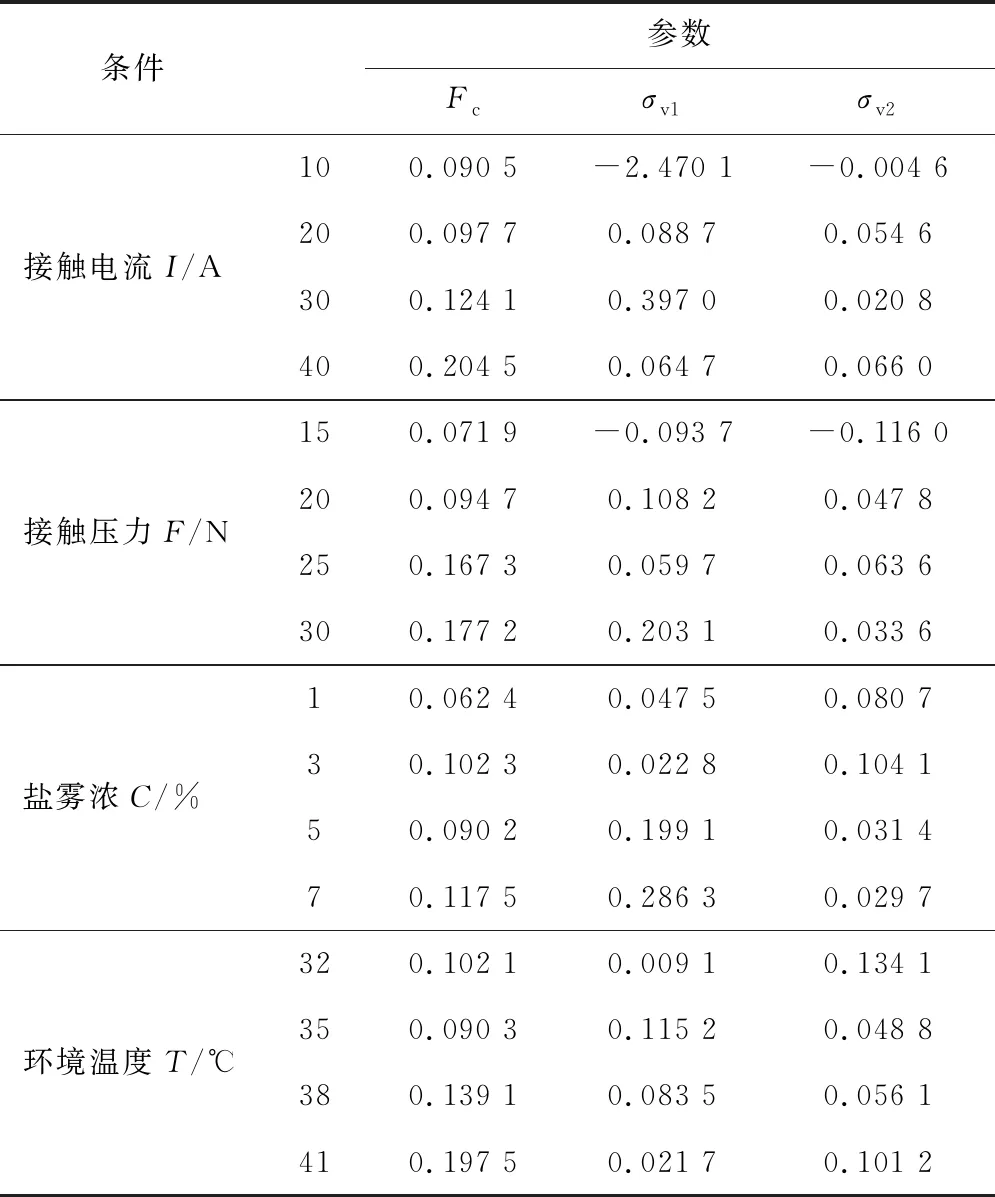
表2 辨識出的參數結果

3.2 磨損量模型參數辨識結果

為了確定Fc(I,F,C,T)、σv1(I,F,C,T)、σv2(I,F,C,T)中參數I、F、C、T最高項的次數，利用MATLAB擬合工具，通過I、F、C、T分別對Fc、σv1、σv2參數進行多項式擬合，辨識結果和擬合結果如圖8～圖10所示。

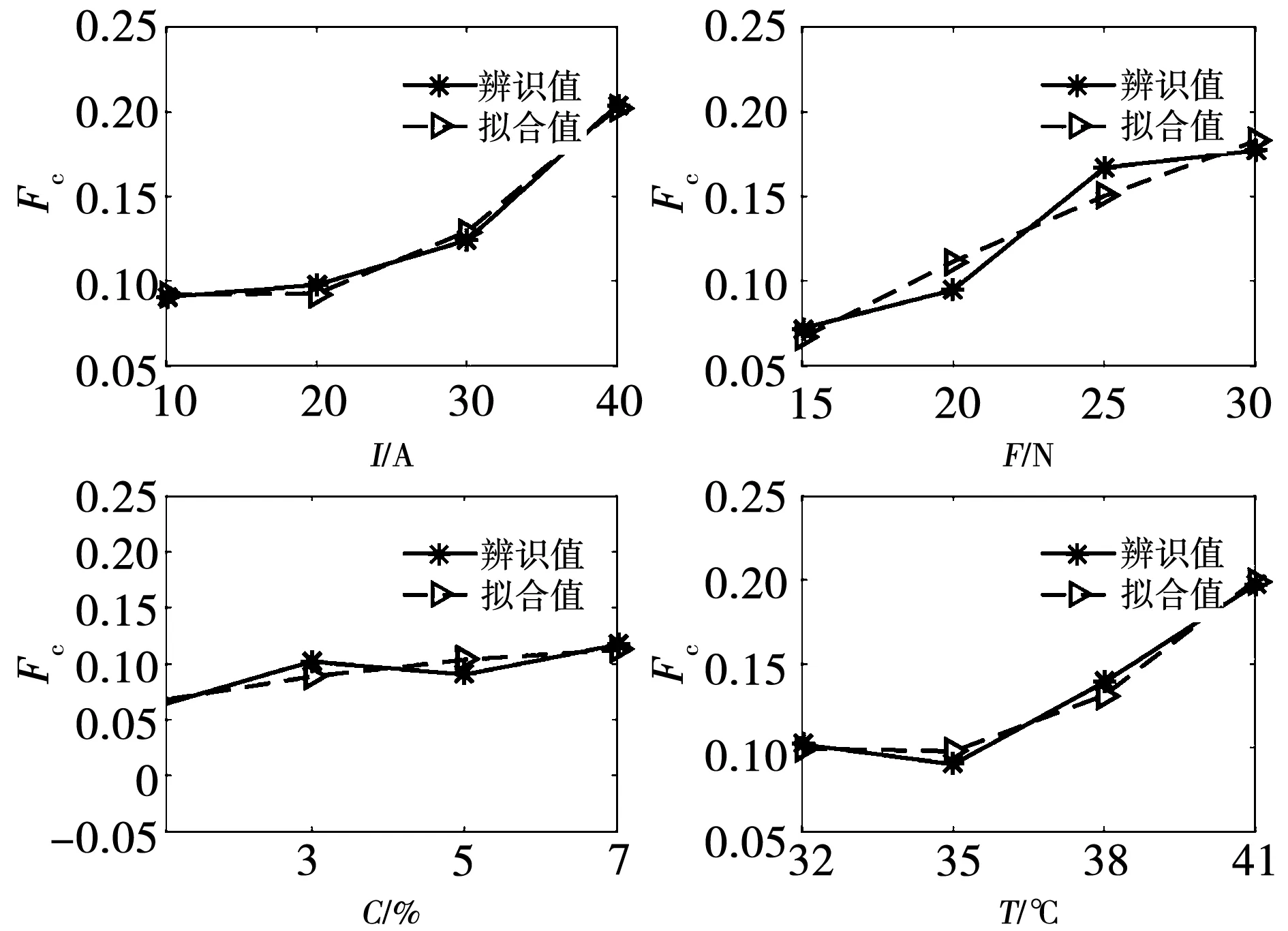
圖8 Fc與I、F、C、T多項式擬合

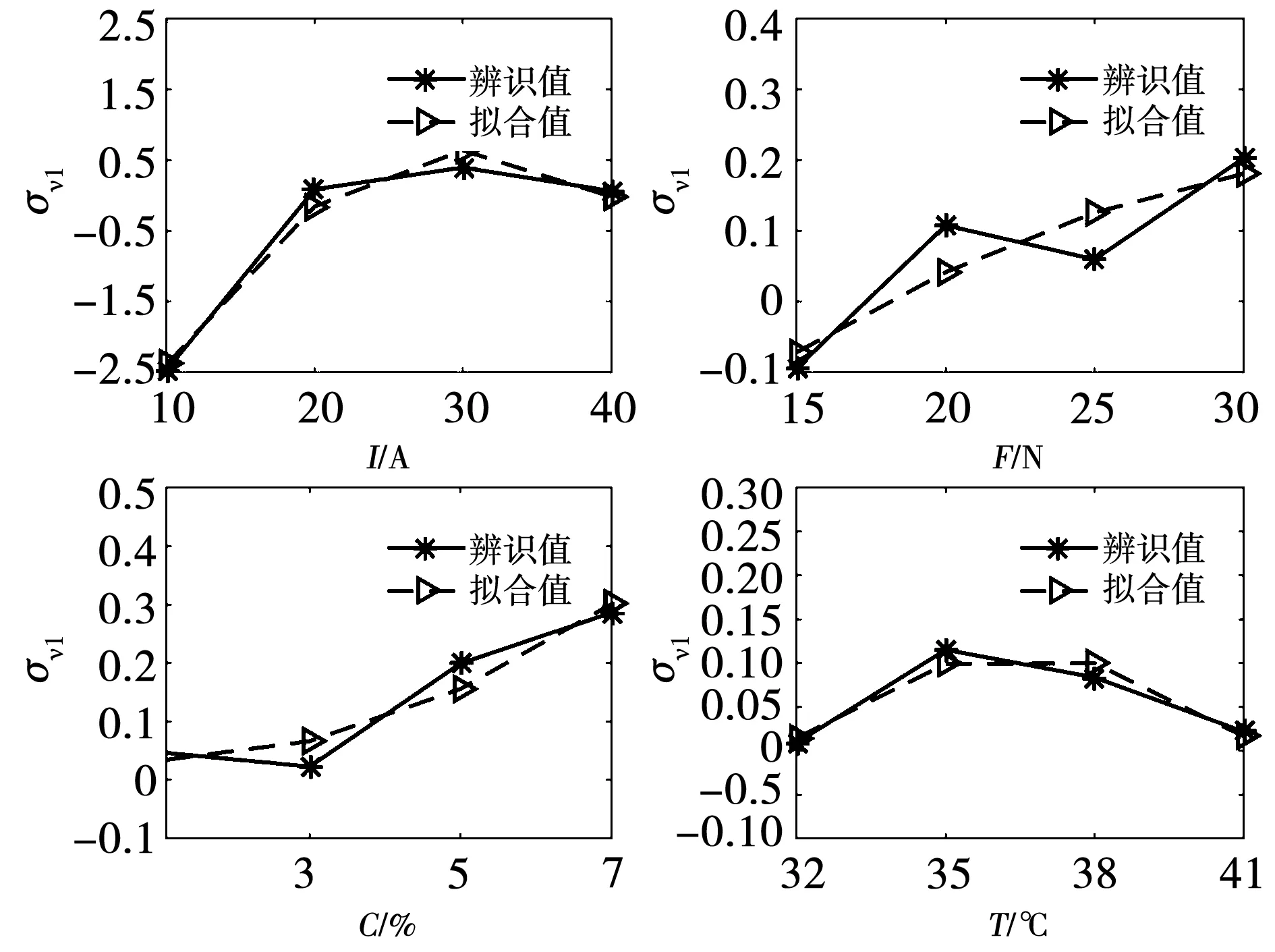
圖9 σv1與I、F、C、T多項式擬合

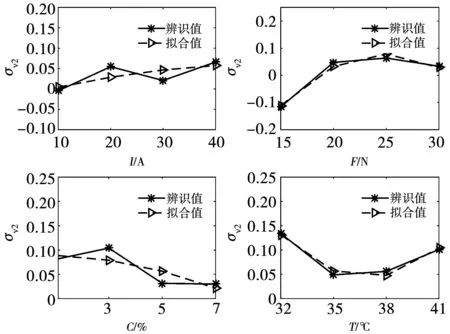
圖10 σv2與I、F、C、T多項式擬合

從圖可知，接觸電流I與參數Fc、σv1、σv2對應二次關系關系；接觸壓力F與參數Fc、σv1、σv2對應二次關系關系；鹽霧濃度C與參數Fc、σv1、σv2對應二次關系；環境溫度T與參數Fc、σv1、σv2對應二次關系關系。因此將Fc(I,F,C,T)、σv1(I,F,C,T)、σv2(I,F,C,T)中參數I、F、C、T最高項的次數為二次，Fc(I,F,C,T)、σv1(I,F,C,T)、σv2(I,F,C,T)可以表示為：

(17)

經過MATLAB多項式擬合，對數據進行分析后，系數如表3所示。由表4知Fc、σv1、σv23個系數的統計量，相關系數R較大，說明有較強相關性；統計量F比較大，說明通過檢驗可能性越大；卡方系數遠小于0.05，說明通過假設檢驗概率為95%；殘差平方和較小，說明擬合效果較好。綜上所述，通過式(17)對參數Fc、σv1、σv2的多項式擬合是正確的。

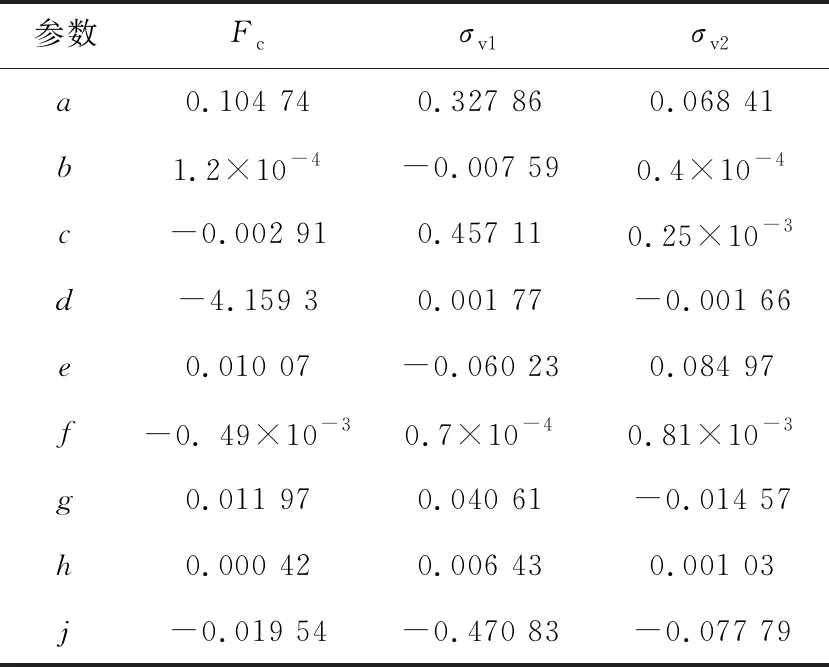
表3 參數Fc、σv1、σv2多項式擬合結果

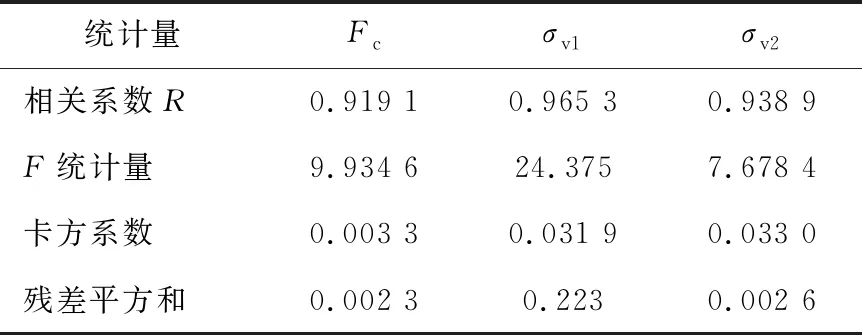
表4 Fc、σv1、σv2的回歸統計量

4 實驗驗證

為了驗證模型的正確性，利用64組實驗數據，計算出普通殘差。繪制殘差圖如圖11所示。

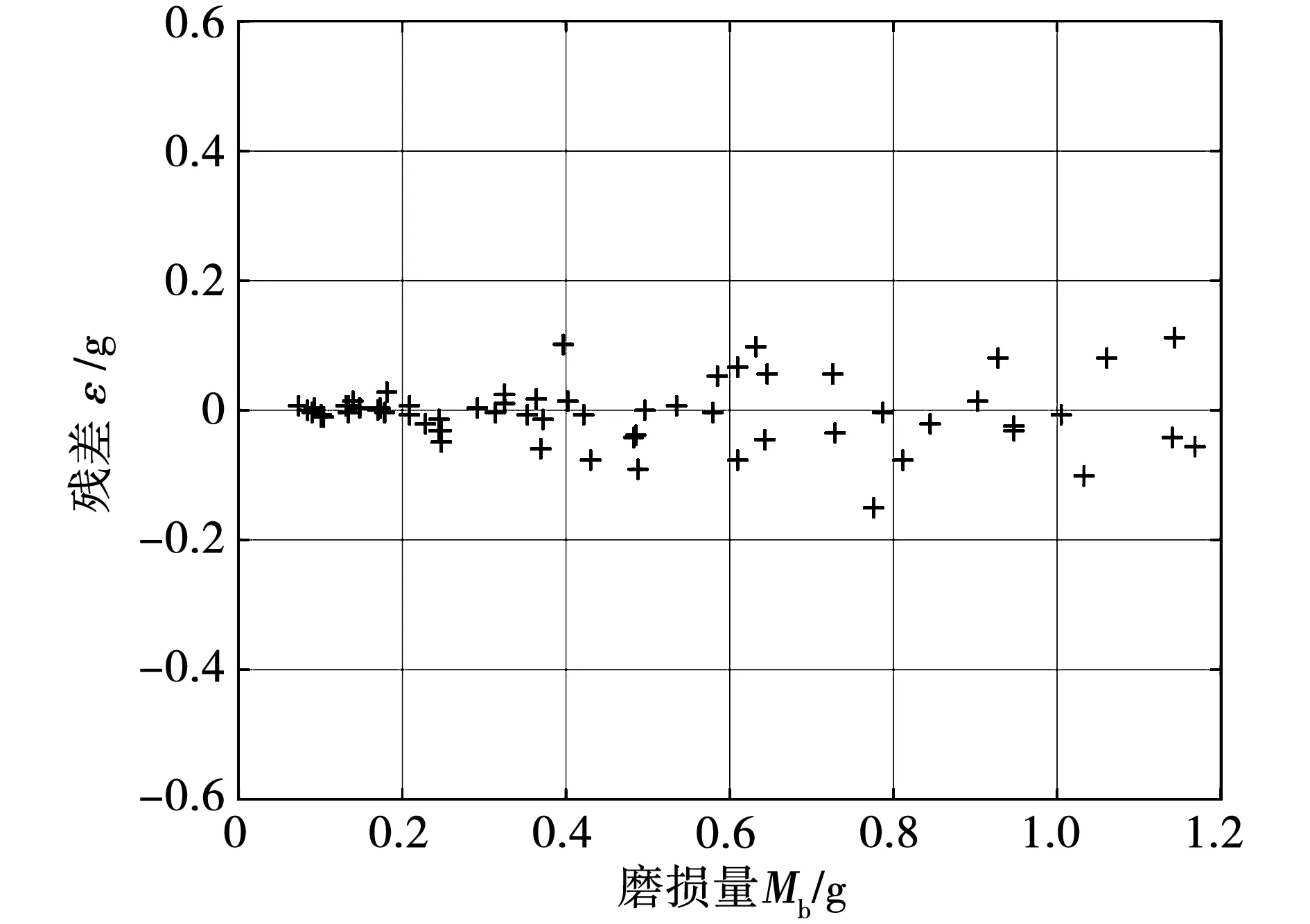
圖11 實驗數據的殘差圖

殘差的計算公式為

(18)

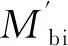
由圖11知，實驗點的誤差都坐落在|εi|≤0.2帶域內，誤差較小，變化規律不規則，文中建立的基于改進的庫倫-粘性摩擦力的磨損量模型可以對鹽霧試驗下的電刷磨損量進行預測。

當I=15 A、F=20 N、C=5%、T=35 ℃；I=25 A、F=20 N、C=5%、T=35 ℃；I=20 A、F=20 N、C=2%、T=35 ℃；I=20 A、F=20 N、C=4%、T=35 ℃時，分別在速度為v=300 r/min(4.7 m/s)、600 r/min(9.4 m/s)、900 r/min(14.1 m/s)、1 200 r/min(18.8 m/s)進行試驗，以滑環圓周線速度為橫坐標，電刷的磨損量為縱坐標，實驗結果以及預測結果如圖12所示。

從圖12知，實驗結果分布在所建立的基于改進的庫倫-粘性摩擦力的磨損量模型曲線附近，最大誤差出現在電流較小速度較大的測量點處，該處絕對誤差達到4.9%，在允許誤差范圍之內，因此該模型可以用來預測電刷在不同條件下的單位時間的磨損量。由于實驗設備及實驗條件所限，該模型的適用速度范圍不超過實驗中采用的異步電機額定轉速1 500 r/min。壓力在電刷滑環系統恒壓彈簧壓力20 N附近，電流在電刷滑環工作電流20 A附近，鹽霧濃度在中性鹽霧試驗標準5%NaCl濃度附近，環境溫度為海洋環境下電刷滑環工作環境溫度38 ℃附近。

5 結 論

1)文中搭建了基于鹽霧試驗機的雙饋電機電刷滑環系統磨損量實驗平臺，該平臺實現了電刷滑環系統和鹽霧試驗機的結合，模擬出海洋環境下電刷滑環系統不同工況下的腐蝕磨損情況，該設備實現了海洋環境下電刷的磨損實驗，實驗結果更加接近真實情況。

2)根據磨損理論，將改進的庫倫-粘性摩擦力模型與電刷磨損量模型結合，建立電刷的磨損量預測模型，實驗表明，接觸電流，接觸壓力，鹽霧濃度，實驗溫度以及速度影響電刷磨損。磨損量建模需將影響磨損量的接觸電流，接觸壓力，鹽霧濃度，實驗溫度以及速度因素引入模型，使模型更加準確。

3)采用粒子群算法進行參數辨識，可以辨識出模型中與接觸電流，接觸壓力，鹽霧濃度，實驗溫度相關的參數，經多項式擬合，得出電刷磨損量的預測模型。經由實驗驗證，該模型正確可靠，可以為運維人員提供一定的運維指導。

由于實驗數據的有限性，該模型預測的結果與實測值之間存在一定的誤差，但在允許范圍之內，加大實驗量和優化預測模型，可使得預測結果更加準確。更深遠地，可以研究故障條件下電刷的磨損量模型。