基于改進灰狼優(yōu)化算法的PMSM滑模自抗擾控制

趙希梅， 陳廣國， 金鴻雁

(沈陽工業(yè)大學 電氣工程學院，遼寧 沈陽 110870)

0 引 言

永磁同步電動機(permanent magnet synch-ronous motor，PMSM)具有高效率、大扭矩慣性比、結(jié)構(gòu)簡單、可控性好的優(yōu)點，在工業(yè)伺服系統(tǒng)中得到廣泛應用[1]。由于PMSM本身具有時變性、非線性、強耦合的特點，當系統(tǒng)受到外部擾動、參數(shù)變化的影響時，傳統(tǒng)的PID控制很難滿足高精確度控制的需求[2-3]。

由我國的韓京清學者提出來的自抗擾控制(active disturbance rejection control，ADRC)一種新的非線性控制方法，因其控制過程中不需要知道控制對象的精確數(shù)學模型和對不確定因素具有強魯棒性而得到廣泛應用[4-5]。文獻[6]提出了一種增強型線性自抗擾控制器，該控制器由兩個線性擴張狀態(tài)觀測器(extended state observer，ESO)組成，對外部擾動和參數(shù)變化具有很好的抑制作用，而不需要精確的PMSM數(shù)學模型。但是傳統(tǒng)ESO的峰值問題沒有得到解決，容易影響觀測精確度。文獻[7]提出一種基于非線性ESO的PMSM全速范圍控制策略，可以快速估計不確定因素并進行補償，相比線性ESO提高了觀測精確度，同時具有更小的峰值。文獻[8]提出一種基于增益連續(xù)ESO的PMSM電流解耦控制方法，增益連續(xù)ESO克服了非線性函數(shù)fal()切換點的突變問題，具有較好的觀測精確度。由于控制器參數(shù)較多，很難認為調(diào)整到最佳性能，同時，灰狼優(yōu)化算法(grey wolf optimizer，GWO)因其算法簡單、需要調(diào)節(jié)參數(shù)少、搜索能力強等優(yōu)點備受青睞[9-10]。文獻[11]提出了一種基于GWO的轉(zhuǎn)矩預測控制方法，采用GWO優(yōu)化了PMSM低速運行時的轉(zhuǎn)矩跟蹤，振動較小，實現(xiàn)了轉(zhuǎn)速和轉(zhuǎn)矩的平滑切換。但是GWO仍然存在一般元啟發(fā)式算法的問題，需要平衡其局部搜索和全局搜索的能力，避免陷入局部最優(yōu)，同時提高搜索速度。由于滑模控制(sliding mode control，SMC)具有對外部擾動和參數(shù)變化不敏感、快速響應的優(yōu)點，本文將SMC代替自抗擾控制中的非線性狀態(tài)誤差反饋(non-linear state error feedback，NLSEF)來提高系統(tǒng)的魯棒性。

基于此，本文提出一種基于改進灰狼優(yōu)化算法(improved grey wolf optimizer，IGWO)的滑模自抗擾控制(sliding mode active disturbance rejection control，SM-ADRC)方案，抑制不確定性的影響并提高PMSM伺服系統(tǒng)的收斂速度。首先，設計(variable gain extended state observer，VGESO)抑制初始峰值，提高觀測精確度；然后依據(jù)觀測值設計滑模控制器，以此提高系統(tǒng)的魯棒性和收斂速度；使用IGWO優(yōu)化SM-ADRC中滑模控制部分的參數(shù)，充分發(fā)揮所設計控制器的性能。通過仿真實驗證明，所提出的控制方案可以在短時間內(nèi)將PMSM的轉(zhuǎn)速跟蹤到給定轉(zhuǎn)速，抑制不確定性因素對系統(tǒng)性能的影響，同時也有效地削弱抖振。

1 PMSM數(shù)學模型

使用Park變換，可以得到d-q坐標下的表貼式PMSM的電壓方程為：

(1)

其中：id、iq和ud、uq分別是d軸和q軸的定子電流和定子電壓；Ld、Lq是d軸和q軸的定子電感，其中Ls=Ld=Lq；ψf是永磁體磁鏈；R是定子電阻；ωe表示轉(zhuǎn)子電角速度。

表貼式PMSM的運動方程為:

(2)

其中：J是轉(zhuǎn)動慣量；ω是機械角速度；Te是電磁轉(zhuǎn)矩；B是粘滯摩擦系數(shù)；TL是負載轉(zhuǎn)矩；p是極對數(shù)。

在id=0的解耦控制下，轉(zhuǎn)矩方程為

(3)

考慮參數(shù)變化和外部擾動，表貼式PMSM的運動方程改寫為

(4)

其中：b0=3Pψf/2J是電流iq的增益項；b1=B/J是轉(zhuǎn)速ω的增益項；b2=1/J是負載轉(zhuǎn)矩TL的增益項。Δ0、Δ1、Δ2為對應增益項的擾動。式(4)可以改寫為

(5)

其中F=Δ0iq-Δ1ω-(b2+Δ2)TL是系統(tǒng)受到的內(nèi)外擾動的總和。

2 PMSM控制系統(tǒng)設計

2.1 傳統(tǒng)ADRC

ADRC是一種對系統(tǒng)內(nèi)外未知擾動實時觀測并進行補償?shù)目刂品椒ǎǜ櫸⒎制?tracking differentiator，TD)、ESO、NLSEF三部分；一階ADRC的結(jié)構(gòu)框圖如圖1所示。

圖1 一階ADRC結(jié)構(gòu)框圖

TD的表達式如下：

(6)

其中：r為ω*的跟蹤信號；R為速度跟蹤因子。

ESO的表達式如下：

(7)

其中：z1是ω的跟蹤信號；z2是擾動總和F的觀測值；β1、β2是誤差校正因子。

NLSEF的表達式為：

(8)

(9)

其中:ex是誤差；αx是非線性因子；δx是濾波因子；x=r、ω、n。

2.2 SM-ADRC設計

傳統(tǒng)ADRC待調(diào)節(jié)的參數(shù)較多，同時由于PMSM速度控制是一階的，不需要二階變量，為了簡化設計，所以設計過程中舍棄TD部分。基于IGWO的PMSM控制系統(tǒng)框圖如圖2所示。

圖2 基于IGWO的PMSM控制系統(tǒng)框圖

由于fal(ex,αx,δx)是分段函數(shù)，是通過切換條件來切換不同的表達式，且切換點的不可導性會使得動態(tài)增益出現(xiàn)突變，嚴重時會導致觀測出來的狀態(tài)量發(fā)生抖振，為了克服這一問題，這里采用一種誤差校正函數(shù)fac()，其表達式為

(10)

其中λ為誤差增益。根據(jù)反正切函數(shù)特性，該函數(shù)可以不用再根據(jù)ex的大小切換表達式，具有連續(xù)可導性。為了獲得“大誤差小增益，小誤差大增益”的校正特性，選取αx=0.5，λ=5 000。

(11)

其中r(t)為變增益，定義為

(12)

VGESO的結(jié)構(gòu)框圖如圖3所示。

圖3 VGESO的結(jié)構(gòu)框圖

在式(11)中，令

(13)

于是式(11)可以改寫為：

(14)

(15)

令eF=z2-x2，L1=β1G1，L2=β2G2，根據(jù)式(14)和式(15)得：

(16)

令γ1=eω，γ2=eF-L1eω，得：

(17)

當忽略擾動F時，上式的特征方程為

λ2+L1λ+L2=0。

(18)

根據(jù)Hurwitz定理，二階系統(tǒng)穩(wěn)定的充分必要條件是L1>0和L2>0。

因為

(19)

則G1、G2>0，推導出當β1、β2>0時，L1和L2大于0，VGESO是穩(wěn)定的。

當系統(tǒng)存在干擾總和F時，系統(tǒng)存在穩(wěn)態(tài)誤差。系統(tǒng)達到平衡狀態(tài)之后，有：

(20)

觀測器的穩(wěn)態(tài)誤差可以表示為

(21)

因此只要β2比ω0大很多，ESO的觀測誤差就會很小，以滿足精確度要求。其中ω0為VGESO的帶寬。

本文，將SMC代替ADRC中的NLSEF，提高此環(huán)節(jié)的魯棒性。為了抑制抖振，采用積分型滑模面

(22)

式中：e0=ω*-z1是期望角速度(ω*)和角速度觀測值(z1)之間的誤差，c是大于0的任意變量。用z2代替擾動總和F，結(jié)合式(5)得

(23)

使用改進型趨近率

(24)

結(jié)合式(23)和式(24)，得

(25)

穩(wěn)定性分析：Lyapunov函數(shù)為

(26)

則

(27)

因此系統(tǒng)穩(wěn)定的。

2.3 IGWO設計

GWO是最近受灰狼的包圍行為和狩獵行為啟發(fā)而提出來的優(yōu)化算法，同時GWO具有等級制度。根據(jù)灰狼的社會行為劃分了4個等級，其中α狼為領導狼，代表最好的最優(yōu)解；以及β狼和δ狼，分別代表第2個和第3個最優(yōu)解，在決策過程中為領導狼提供幫助；而γ狼按照命令行動。GWO的各狼等級如圖4所示。

圖4 灰狼等級圖

包圍行為可以用數(shù)學模型表示為：

D=|CXp(t)-X(t)|；

(28)

X(t+1)=Xp(t)-AD。

(29)

其中：Xp(t)和X(t)分別代表獵物和灰狼的位置，D為獵物與灰狼的距離，X(t+1)為灰狼根據(jù)獵物位置進行包圍行為的下一個位置。A和C為控制系數(shù)，為：

A=2ar1-a；

(30)

C=2r2。

(31)

其中：r1和r2為[0,1]的隨機變量。收斂因子a在迭代過程中從2線性下降到0。

狩獵行為可以用數(shù)學模型表示為：

(32)

(33)

(34)

定義目標函數(shù)為

(35)

其中N為采樣總數(shù)。

由于，收斂因子a是線性遞減的，沒有充分發(fā)揮灰狼的探索能力，容易造成早熟問題。所以采用改進收斂因子

(36)

其中：t為當前的迭代次數(shù)；tmax為最大迭代次數(shù)；rand()為0到1的任意值。

3 系統(tǒng)仿真實驗分析

為了驗證IGWO的求解能力，本文選擇5個標準測試函數(shù)，分別采用IGWO、GWO、粒子群(particle swarm optimization，PSO)進行求解。標準測試函數(shù)如表1所示。

表1 標準測試函數(shù)

在MATLAB上對進行測試，最大迭代次數(shù)設置為500，得到如圖5所示的函數(shù)值收斂曲線。

圖5 函數(shù)值收斂曲線

從函數(shù)值收斂曲線可以得出，在5種標準測試函數(shù)測試下，IGWO的收斂速度比GWO、PSO更快，同時IGWO的求解精確度也比GWO、PSO的更高。

采用Link-RT半實物仿真平臺進行實驗驗證，半實物仿真平臺如圖6所示。主要包括上位機、Link-BOX實時仿真機、扭矩傳感器、伺服電機、伺服驅(qū)動器等。

圖6 半實物仿真平臺

為了驗證本文的改進SM-ADRC的有效性，PMSM伺服系統(tǒng)分別采用ADRC、傳統(tǒng)SM-ADRC(傳統(tǒng)滑模+ESO)、改進SM-ADRC進行實驗對比。基礎條件可以設置為：逆變器的給定電壓為Udc=311 V；SVPWM的開關切換頻率設置可以為f=10 kHz，采樣周期Ts=10 μs，相對誤差可以設置為0.000 1。PMSM的參數(shù)如表2所示。

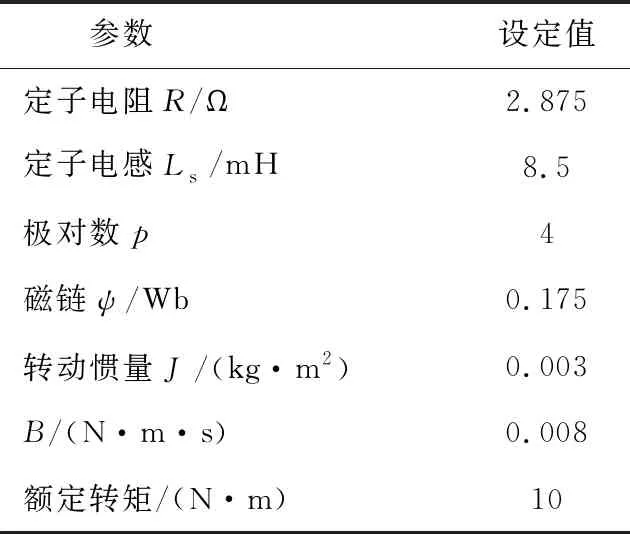
表2 電機參數(shù)

為了充分發(fā)揮控制器的性能，采用IGWO分別對ADRC、傳統(tǒng)SM-ADRC、改進SM-ADRC的參數(shù)進行優(yōu)化，優(yōu)化流程如圖7所示。IGWO的最大迭代次數(shù)tmax=100，運行程序得到ADRC的控制參數(shù)為：R=6 500，αr=0.4，δr=0.01，β1=8 500，β2=500 000，αω=0.9，δω=0.01，β3=5 000，αn=0.9，δn=0.01；傳統(tǒng)SM-ADRC的控制參數(shù)：c=50，η=204.09，k=326.21，β1=8 500，β2=500 000，αω=0.9，δω=0.01。改進SM-ADRC的控制參數(shù)：c=2 527.4，ε=0.1，η=1 451，K=0.3，β1=8 500，β2=90 000 000。

圖7 IGWO算法參數(shù)優(yōu)化流程圖

工況一，為了驗證改進SM-ADRC的跟蹤性能，PMSM伺服系統(tǒng)空載，在0時刻給定轉(zhuǎn)速設置為1 000 r/min，0.2 s時刻給定轉(zhuǎn)速設置為1 500 r/min，3種控制方法的空載轉(zhuǎn)速響應曲線如圖8、圖9、圖10所示。從圖8可知，在空載的情況下，ADRC轉(zhuǎn)速上升到1 000 r/min時的超調(diào)為3 r/min，在0.07 s時刻電機轉(zhuǎn)速穩(wěn)定在設定值1 000 r/min；ADRC轉(zhuǎn)速上升到1 500 r/min時的超調(diào)為1 r/min，在0.21 s時刻電機轉(zhuǎn)速穩(wěn)定在設定值1 500 r/min。從圖9可知，傳統(tǒng)SM-ADRC轉(zhuǎn)速上升到1 000 r/min時的超調(diào)為1 r/min，在0.012 s時刻電機轉(zhuǎn)速穩(wěn)定在設定值1 000 r/min；傳統(tǒng)SM-ADRC轉(zhuǎn)速上升到1 500 r/min時的超調(diào)為0.5 r/min，在0.21 s時刻電機轉(zhuǎn)速穩(wěn)定在設定值1 500 r/min。從圖10可知，改進SM-ADRC轉(zhuǎn)速在接近1 000 r/min時趨近速度降低，沒有出現(xiàn)超調(diào)，在0.009 s時電機轉(zhuǎn)速能穩(wěn)定在1 000 r/min；改進SM-ADRC轉(zhuǎn)速在接近1 500 r/min時趨近速度降低，又沒有出現(xiàn)超調(diào)，在0.21 s時電機轉(zhuǎn)速能穩(wěn)定在1 500 r/min。說明空載情況下，改進SM-ADRC下PMSM的速度可以快速跟蹤設定值，同時有效地抑制了峰值問題，沒有出現(xiàn)超調(diào)。

圖8 ADRC空載轉(zhuǎn)速響應曲線

圖9 傳統(tǒng)SM-ADRC空載轉(zhuǎn)速響應曲線

圖10 改進SM-ADRC空載轉(zhuǎn)速響應曲線

工況二，為了驗證改進SM-ADRC的抗干擾能力，初始給定轉(zhuǎn)速設置為1 000 r/min，在0.2 s時刻加10 N·m的固定負載轉(zhuǎn)矩，3種控制方法的負載轉(zhuǎn)速響應曲線如圖11、圖12、圖13所示。從圖11、圖12、圖13可知，施加10 N·m固定負載轉(zhuǎn)矩后，ADRC的轉(zhuǎn)速下降到959.8 r/min，在0.25 s才回到設定值；傳統(tǒng)SM-ADRC的轉(zhuǎn)速下降到980 r/min，在0.203 s轉(zhuǎn)速回到設定值；改進SM-ADRC的轉(zhuǎn)速下降到982 r/min，在0.203 s轉(zhuǎn)速就回到了設定值。說明改進SM-ADRC具有更好的抗干擾能力。

圖11 ADRC負載轉(zhuǎn)速響應曲線

圖12 傳統(tǒng)SM-ADRC負載轉(zhuǎn)速響應曲線

圖13 改進SM-ADRC空載轉(zhuǎn)速響應曲線

工況三，在工作環(huán)境發(fā)生變化時，PMSM的內(nèi)部參數(shù)會受到外界因素的影響，為了驗證改進SM-ADRC在參數(shù)變化之后轉(zhuǎn)速的跟蹤性能和抗干擾能力，將控制器中的電機參數(shù)(J和B)調(diào)整為原來的2倍，在0時刻給定轉(zhuǎn)速設置為1 000 r/min；然后在0.2 s處，對PMSM施加10 N·m的固定負載擾動，得到3種控制方法的轉(zhuǎn)速響應曲線如圖14、圖15、圖16所示。從圖14可知，ADRC轉(zhuǎn)速的超調(diào)為3 r/min，在0.06 s才穩(wěn)定在設定值；ADRC在受到10 N·m的固定負載轉(zhuǎn)矩后，轉(zhuǎn)速下降到959.4 r/min，在0.26 s時轉(zhuǎn)速才回到設定值。從圖15可知，傳統(tǒng)SM-ADRC的超調(diào)為0.5 r/min，振蕩0.004 s后才達到穩(wěn)定；傳統(tǒng)SM-ADRC在受到10 N·m的固定負載轉(zhuǎn)矩后，轉(zhuǎn)速下降到982 r/min，在0.201 s時轉(zhuǎn)速才回到設定值。從圖16可知，改進SM-ADRC轉(zhuǎn)速沒有超調(diào)，且在0.01 s就穩(wěn)定在設置值；改進SM-ADRC在受到10 N·m的固定負載轉(zhuǎn)矩后，轉(zhuǎn)速下降到984 r/min，之后迅速回到設定值，沒有振蕩和穩(wěn)態(tài)誤差。說明改進SM-ADRC在電機參數(shù)發(fā)生變化之后，相比ADRC和傳統(tǒng)SM-ADRC超調(diào)小，對負載轉(zhuǎn)矩擾動的響應速度快且不造成振蕩，對參數(shù)變化具有很好的抑制作用。

圖14 ADRC參數(shù)變化轉(zhuǎn)速響應曲線

圖15 傳統(tǒng)SM-ADRC參數(shù)變化轉(zhuǎn)速響應曲線

圖16 改進SM-ADRC參數(shù)變化轉(zhuǎn)速響應曲線

4 結(jié) 論

為了提高PMSM伺服系統(tǒng)的抗干擾能力，本文提出了一個基于IGWO的改進SM-ADRC方法。采用VGESO觀測PMSM伺服系統(tǒng)所受到的不確定因素，同時抑制峰值問題對觀測精確度的影響；采用SMC代替NLSEF提高了控制系統(tǒng)的魯棒性。然后用IGWO對參數(shù)進行優(yōu)化，充分的顯示出本文的改進SM-ADRC比ADRC、傳統(tǒng)SM-ADRC具有更好的魯棒性，為實際的伺服系統(tǒng)應用提供了新方法。