基于三次貝塞爾曲線的軌跡規劃方法

廈門大學航空航天學院 江浩 彭俠夫

四足機器人在復雜環境下既能夠實現靜態行走，又能夠以動態方式高速運動，具有較高的研究價值。而足端軌跡研究則是四足機器人運動的基礎。對四足機器人建立了簡化模型，并對單腿的運動學和動力學進行建模。然后在運動學上根據彈簧負載倒立擺模型選取落腳點，軌跡上選取三次貝塞爾曲線進行改進由彈簧負載倒立擺模型和三次貝塞爾曲線生成足端軌跡，彈簧負載倒立擺模型獲取足端落地平衡點保證機器人支撐相與擺動相切換時的平穩。三次貝塞爾曲線結合地形生成規避障礙物的足端軌跡，對曲線生成方式進行改進使其符合零沖擊步態的規劃，在動力學上應用拉格朗日方程獲得了驅動力矩與足端軌跡的映射關系，最后通過傳感器計算實際足端軌跡與規劃足端軌跡的誤差建立虛擬動力學方程實現反饋控制，提高了四足機器人抗干擾能力，降低了單腿高速擺動及落地沖擊對機身運動狀態的影響。

腿足仿生機器人根據腿的數量又分為雙足、四足、六足等多足機器人。參照哺乳類四足動物設計的仿生四足機器人相較于雙足仿生機器人更穩定、靈活、負載高，相較于六足等多足仿生機器人結構復雜度低、易于控制，在復雜環境下既能夠實現靜態行走，又同時能夠以動態方式高速運動。綜合運動特性及結構復雜度，四足機器人的適應性更廣，可研究價值更高[1，2]。

1 四足機器人模型

1.1 四足機器人簡化模型

根據四足機器人簡化模型確定世界坐標系和機身坐標系。機身質心位置為機身坐標系原點，設計足端軌跡時，足端軌跡坐標以初始站立姿態足端相對機身坐標系的固定位置為足端軌跡坐標原點，整機的運動方向為正方向。單腿可視作具有三自由度的三連桿，四足機器人的簡化模型及坐標系定義如圖1所示。

1.2 D-H 法運動學方程

對連桿系統進行建模的一種通用方法為D-H 法，在各個連桿上設置坐標系，根據連桿的連接結構與空間關系建立變換矩陣，從連桿一端根據連桿間的變換矩陣逐步計算下一連桿一端的空間矩陣，最終計算出連桿兩端間的空間變換矩陣，即四足機器人的運動學方程。

坐標系的變換矩陣T 由坐標系旋轉變換矩陣R 和坐標系位移矩陣P 組成，旋轉矩陣R 是指兩坐標系原點重合對應的坐標系、三軸的方向余弦，位移矩陣P 是變換后的坐標系相對于參考坐標系的三個方向位移。其變換矩陣構成如公式（1）所示。

連桿間的坐標系變換由連桿偏距di、連桿長度li、連桿扭轉角φi、連桿間旋轉角θi四個運動學模型參數來描述，連桿長度和連桿扭轉角為連桿自身的物理參數，連桿偏距和連桿間夾角為連桿連接物理參數。在四足機器人單腿模型中，腿部連桿均不存在扭轉，由此可以確定單腿從機身和大腿連接處到足端的坐標變換矩陣。各物理參數如圖1所示，機身與單腿連接處即臀關節為初始坐標系，臀、大腿、小腿長度分別為l1、l2、l3，臀部與機身關節、臀部與大腿關節、大腿與小腿關節角度分別為θ1、θ2、θ3，D-H 法的參數表如表1所示。

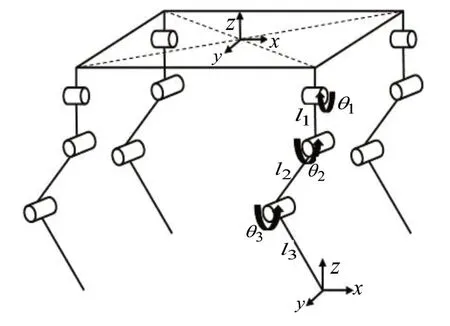
圖1 四足機器人簡化模型Fig.1 Simplified model of quadruped robot

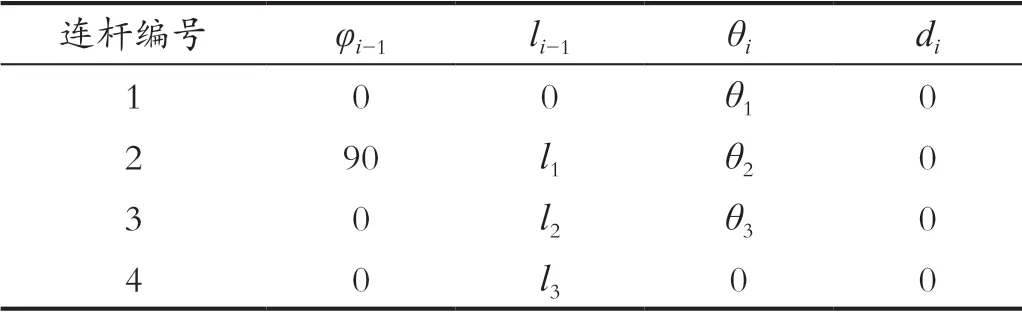
表1 四足機器人機身到足端的D-H 參數Tab.1 D-H parameters from the quadruped robot body to the foot end

根據D-H 參數法建立關節角度、角速度、角加速度與足端位移、速度、加速度間的映射關系，為動力學模型計算提供基礎。

2 足端軌跡規劃

2.1 虛擬彈簧負載倒立擺

倒立擺模型最早用于雙足機器人步態控制，該理論提出以倒立擺接觸點為核心，根據落點與平衡位置的關系來控制彈簧倒立擺的加速、勻速、減速運動。若落足點位于平衡點后方則為減速狀態；若落足點位于平衡點前方則為加速狀態；若落足點位于平衡點則為勻速運動狀態[3]。在四足機器人運動過程中，分為支撐相與擺動相，可將擺動相的腿虛擬為彈簧負載倒立擺，根據機身狀態及指令計算足端軌跡擺動相落點控制四足機器人機身跟蹤狀態指令運動。彈簧負載倒立擺如圖2所示。

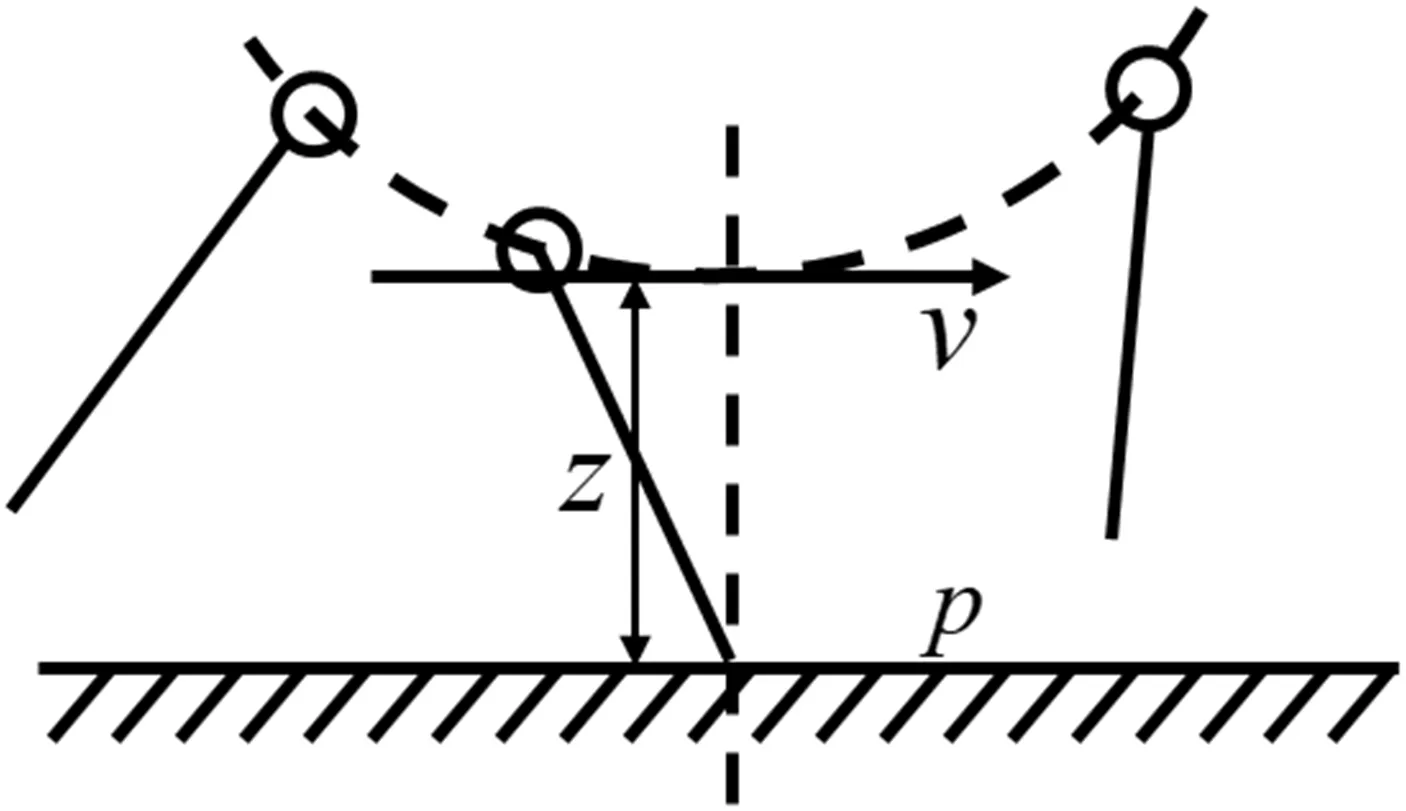
圖2 彈簧負載倒立擺模型Fig.2 Spring-loaded inverted pendulum model

四足機器人擺動腿虛擬為彈簧負載倒立擺，其平衡點取決于機身速度v、擺動周期Tsw、擺動腿的最大抬腿高度hsw、指令機身速度vref，此處計算速度機身x、y方向平衡點位置如公式（2）所示：

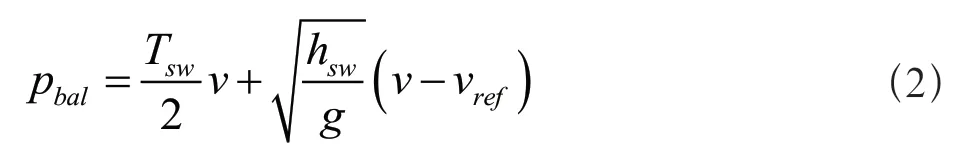
2.2 三次貝塞爾曲線

根據腿部傳感器可以計算出四足機器人支撐相切換為擺動相時腿部足端的位置，結合彈簧負載倒立擺模型可計算得四足機器人落地平衡點。四足機器人為適用于復雜地形設計的機器人，在其結合三維地圖傳感器或激光雷達傳感器生成三維地圖時，四足機器人擺動相軌跡及落點需要靈活根據地圖調整，保持機身平穩性。

三次貝塞爾曲線是應用于二維圖形的數學曲線，通常是用于計算機矢量作圖，n次貝塞爾曲線是由n+1 個點組合而成，曲線可以通過改變節點位置生成。在曲線生成過程中也可以通過拖動節點實時更改未完成的曲線軌跡，應用于四足機器人擺動相軌跡的生成，既能夠結合彈簧負載倒立擺模型生成軌跡，還能夠在運行過程中根據三維地圖實時調整軌跡。三次貝塞爾曲線的基本方程如公式（3）所示：

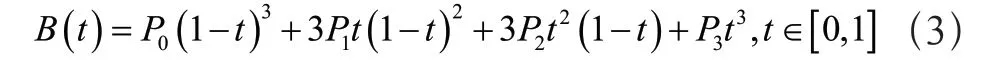
其中P0、P1、P2、P4為軌跡生成的四個基礎坐標，P0為支撐相切換為擺動相時足端所處位置，P4為根據彈簧負載倒立擺生成的落足點位置，通過調整P1、P2的位置可以控制足端擺動的高度等參數，以此來實現規避障礙物等功能。在原方程中t為每一段中點位置位于當前線段中的比例，若直接將其作為擺動周期時間的等比例縮放，在求導后獲取擺動相軌跡的速度時，其速度初始不為零，此處將原式中的t替換為與時間有關的比例公式，則方程如公式（4）所示：

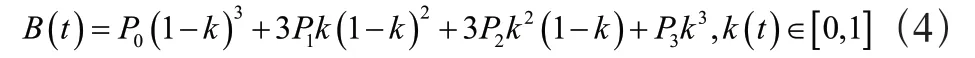
此處時間t為單腿從支撐相切換到擺動相開始到擺動相結束。四足機器人關節控制方式為力控制，因此加速度可突變，不考慮初始加速度為零的情況，僅考慮求導后兩端點值均為零，且該函數為從0 到1 為遞增函數，本文采用的比例函數如公式（5）所示：

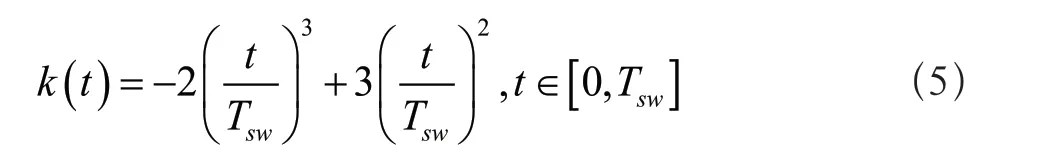
將替換后的三次貝塞爾曲線對時間求導可以得到足端軌跡速度、加速度。如公式（6）、公式（7）所示：

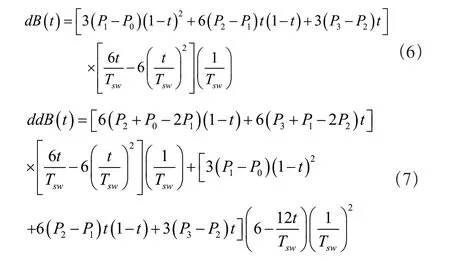
由此獲得初始速度和終點速度均為零的三次貝塞爾曲線方程及速度、加速度方程。該方程用于規劃擺動相的足端軌跡，獲取擺動腿末端的運動狀態，結合運動學方程的逆解可得到關節轉角所需的角度、角速度、角加速度作為關節控制的目標量，然后通過單腿動力學計算電機的按照規劃的三次貝塞爾曲線運動所需的力矩。

3 實驗

3.1 ADAMS 與Simulink 聯合仿真

四足機器人為強非線性、強時變系統，該系統用力控制方法在地面行走時具有不確定性，四足機器人在行走中參數不斷變化，與地面交互接觸面小，系統必須能夠準確及時的對四足機器人的四條腿、機身的所有狀態共49 個狀態量進行反饋并實現閉環控制。在進行實物樣機運行前，必須由計算機仿真調整控制參數使得近似的建模模型具有理想的控制效果。建立整機模型的程序框圖如圖3所示。

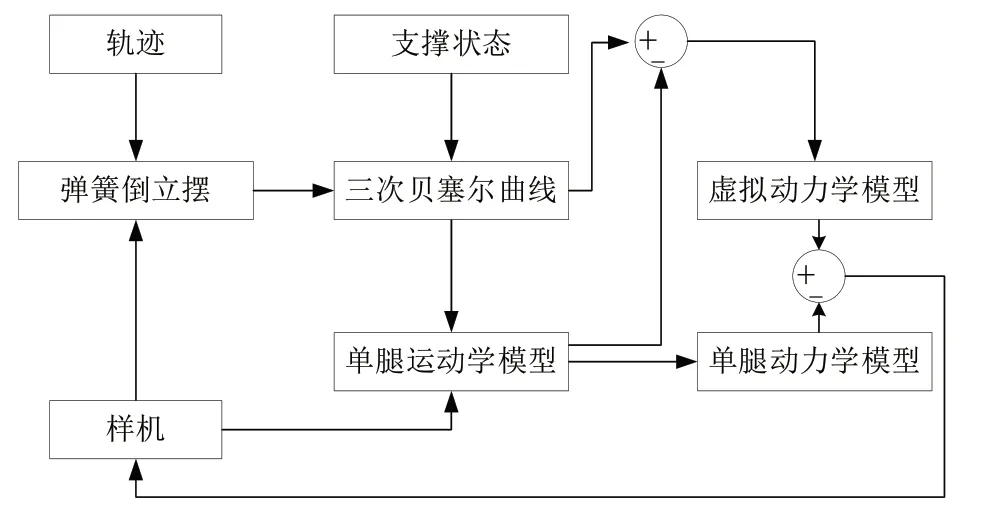
圖3 單腿擺動相控制框圖Fig.3 Block diagram of single-leg swing phase control

目前常用的機器人力學控制方法是由Simulink 控制的數學模型和ADAMS 導入的四足機器人建模模型生成的動力學模型聯合仿真驗證效果。整體思路為：Simulink 中建立控制器中的運動學、動力學、模型預測控制等數學模型，搭建能夠實現對四足機器人狀態數據即規劃軌跡完成力控輸出的整體控制框架。SoildWorks 建立物理樣機的3D 模型，將軟件生成的3D 模型導入ADAMS，建立連接關系和驅動器，設置輸入和輸出量，構建控制系統。由Simulink 的模型于ADAMS 的物理樣機動力學模型數據交互實現仿真控制。

軌跡生成器主要功能為接受上層算法或遙控的控制指令，其指令包括運動方向、旋轉角、速度、預設步態類別。該運動方向指四足機器人不改變機體朝向，僅改變整機的運動方向，主要用于實現側向行走。旋轉角指機身朝向，但不影響四足機器人的運動方向，可以實現機身直線運動過程中的機身旋轉，完成四足機器人作為移動平臺需要完成的其他任務。速度僅指前進方向，通過運動方向分解為世界坐標系下x與y軸方向的運動速度。步擺動相控制器主要功能是接收到平衡控制器發送的腿部擺動指令、擺動腿的位置關系、四足機器人腿部編碼器反饋的腿部狀態數據。在擺動相控制器接受四足機器人腿部狀態數據，該數據包括關節角度、角速度、角加速度，同時四足機器人軌跡中的速度，包括目標速度與實際速度，機身軌跡速度用于落足點計算。由于該方法用于優化負載控制，未考慮環境變化和地形識別方法，因此軌跡控制參數固定，并內置到擺動相控制器中，根據抬腿高度自動生成軌跡。然后將生成的軌跡包括足端位置、速度、加速度和關節傳感器反饋的角度、角速度、角加速度帶入動力學方程得出目標軌跡的力矩。再將傳感器反饋的腿部關節角度、角速度、角加速度由運動學正解計算出四足機器人實際的足端狀態即足端實際的位置、速度、加速度，根據列出的控制參數調整的動力學微分方程，計算反饋的足底力，再將反饋計算的足底力通過傳感器反饋的關節角度映射為關節力矩作為反饋調節量。擺動相控制器輸出的為目標軌跡的控制力矩與足端動力學微分方程計算的反饋力矩的求和。

3.2 單腿實驗仿真

單腿實驗主要驗證擺動相控制器的力控制跟蹤效果。驗證內容為軌跡生成器生成的軌跡狀態即位置、速度、加速度是否符合設計需求；動力學模型開環控制是否有效；動力學微分方程進行的驅動器力補償是否能夠滿足軌跡跟蹤。

足端軌跡初速度與末速度均為0，在力控制條件下，加速度屬于可突變項，因此無需考慮其初始和末端加速度不為0 的情況。足端軌跡狀態量如圖4所示。

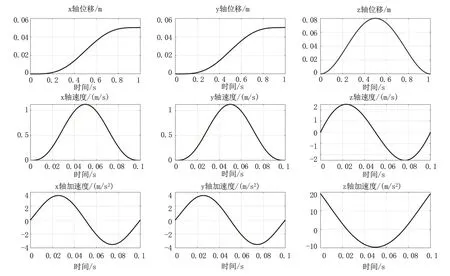
圖4 三次貝塞爾曲線足底軌跡狀態量Fig.4 Cubic Bezier curve plantar trajectory state quantity

3.3 整機控制實驗

整機控制實驗首先要驗證平衡控制器的支撐力優化效果，然后驗證該四足機器人實現Trot 基本步態。四足機器人仿真模型如圖5所示。

圖5 ADAMS 四足機器人模型Fig.5 ADAMS quadruped robot model

本文支撐相方法采用靜力學分配的方式，通過速度增加橫向足底力以此保證支撐相的足端軌跡。結合本文優化后的三次貝塞爾曲線軌跡的力控解算方法可獲得單腿關節力矩。實際的足端軌跡及與本文方法生成的規劃軌跡如圖6所示。

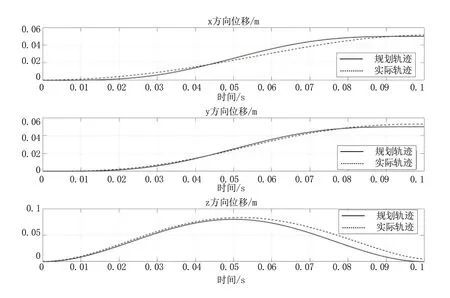
圖6 規劃與實際的足端軌跡對比圖Fig.6 Comparison of planned and actual foot trajectories

四足機器人應用本文控制方法在Tort 步態下的機身狀態，四足機器人狀態變化規律，沒有產生突變，證明該方法能夠有效避免擺動相落地沖擊及擺動時的動能影響。

4 結語

通過機身狀態計算出落地平衡點，結合地形信息計算中間控制點，可以生成具有地圖適應性的零沖擊足端軌跡，降低落地時對機身狀態產生的影響。同時對三次貝塞爾曲線進行了優化，降低了擺動腿自身在運動過程中擺動對機身造成的影響，使其能夠相互抵消，機身狀態規律變化，實現動態平穩。