基于田口方法與灰色關聯分析的碰撞射流通風系統優化

齊賀闖， 葉 筱， 亢燕銘， 鐘 珂

(1.上海工程技術大學 機械與汽車工程學院， 上海 201620；2.東華大學 環境科學與工程學院， 上海 201620)

“碳達峰”“碳中和”已列為中國未來幾十年的重要發展戰略。據統計，通風、空調能耗占建筑總能耗的50%以上[1]。為加速實現“碳中和”目標，如何使建筑通風、空調系統更綠色高效已成為暖通空調行業無法回避的現實考題。

合理的氣流組織是營造良好室內熱環境、改善室內空氣品質和提高通風效率的關鍵[2]。Gao等[3]研究指出，因送風設計參數如送風速度和溫度、送風口形狀等對室內氣流組織具有耦合影響，在進行空調系統設計時，合理匹配設計參數之間的關系是需要考慮的主要因素之一。此外，理想空調系統預期達到的目標是在兼顧節能的同時維持良好室內熱舒適和空氣品質，但是，這些評價指標對系統整體通風性能的優化存在相互制約關系，比如，維持良好室內熱舒適所對應的設計變量組合可能導致較差的室內空氣品質，或雖實現了節能目標，但不能提供良好的室內熱舒適[4-5]。因此，將上述通風性能評價指標同時考慮在內是進行通風、空調系統優化設計的另一關鍵因素。

碰撞射流通風(impinging jet ventilation，IJV)是近幾年逐漸發展起來的一種新型通風策略，可同時實現節能、提供良好室內熱舒適和空氣品質的目標，且兼顧供冷和供暖功能[6-8]。雖然大量研究針對IJV的通風性能展開，但這些研究均將衡量IJV通風性能優劣的指標(如室內熱舒適、空氣品質及節能特性等)單獨進行分析[6-10]，很少有文獻對這些評價指標同時進行優化研究。此外，關于設計變量與通風性能之間匹配關系的研究大多借助單因素試驗方法，因素間交互作用對整體通風性能的影響尚不明確。因此，如何合理匹配設計參數間的組合關系使IJV整體通風性能達到最優，成為目前應重點關注的問題。

以一個典型雙人辦公室為研究對象，提出一種基于田口方法和灰色關聯分析相結合的IJV多目標同時優化方法，解決IJV的多目標、多設計參數同時優化問題。首先，以送風口高度、送風速度和送風溫差為研究變量(即設計變量)，以室內熱舒適(如頭足溫差Δt和吹風感Dr)、空氣質量(如呼吸區空氣齡τbz)和系統節能特性(如送風能量利用系數η)為目標變量，利用田口試驗方法研究上述設計變量對各目標變量影響的顯著性。在此基礎上，借助統計學理論中的灰色關聯分析法將多目標同時優化問題轉化為單目標優化，并給出IJV整體通風性能達到最優時的設計變量匹配關系。最后，通過試驗對所獲得的最佳組合條件進行合理性驗證。研究結果不僅可為IJV的優化設計提供理論指導，而且可為暖通空調領域多目標同時優化問題提供新思路。

1 試驗設計與數值計算模型

1.1 田口方法的試驗設計

田口方法(Taguchi method)[11]以誤差因素模擬各種干擾，運用信噪比RS/N作為穩健性指標(即質量評價指標)，從而尋求最優試驗設計方案。文獻[6]指出，影響IJV通風性能的主要設計參量包括送風速度、送風溫差、送風口高度、回風口高度等。考慮到目前辦公建筑大多采用回風口和排風口共用的回/排風方式，本文僅選取送風口高度h、送風速度vs和送風溫差Δts共3個因素作為研究變量。選取頭足溫差Δt、吹風感Dr作為室內熱舒適性的評價指標，呼吸區(取距離地面1.1 m高度的區域)空氣齡τbz作為室內空氣質量的評價指標，送風能量利用系數η作為節能特性的評價指標[12]。

根據田口試驗方法，將上述3個研究變量分別設定在高(3)、中(2)、低(1)3個水平。采用田口試驗中的L9(33)正交表制定試驗方案，如表1所示。

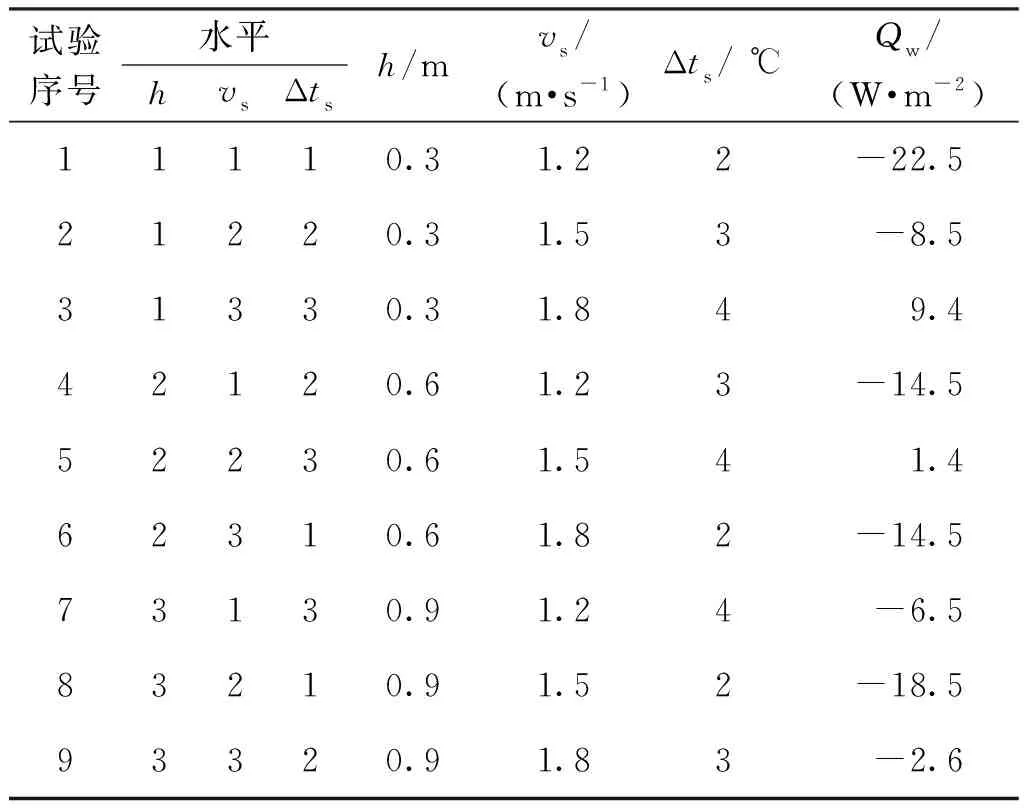
表1 田口試驗L9(33)正交表Table 1 Taguchi’s L9(33) orthogonal array

1.2 計算流體動力學數值模擬

1.2.1 物理模型及邊界條件

以一個房間尺寸長為3.6 m(x)、寬為4.2 m(y)、高為2.7 m(z)的雙人辦公室為研究對象，該房間的3 D透視圖如圖1所示。IJV的送風管道為半圓形，緊貼北墻布置，送風口直徑為0.4 m，距離地面的高度為h。回風口布置在屋頂中央，尺寸為0.3 m×0.2 m。另外，在外墻側設有一扇尺寸為4.2 m×1.2 m的窗戶(見圖1)，窗墻面積比為0.44。

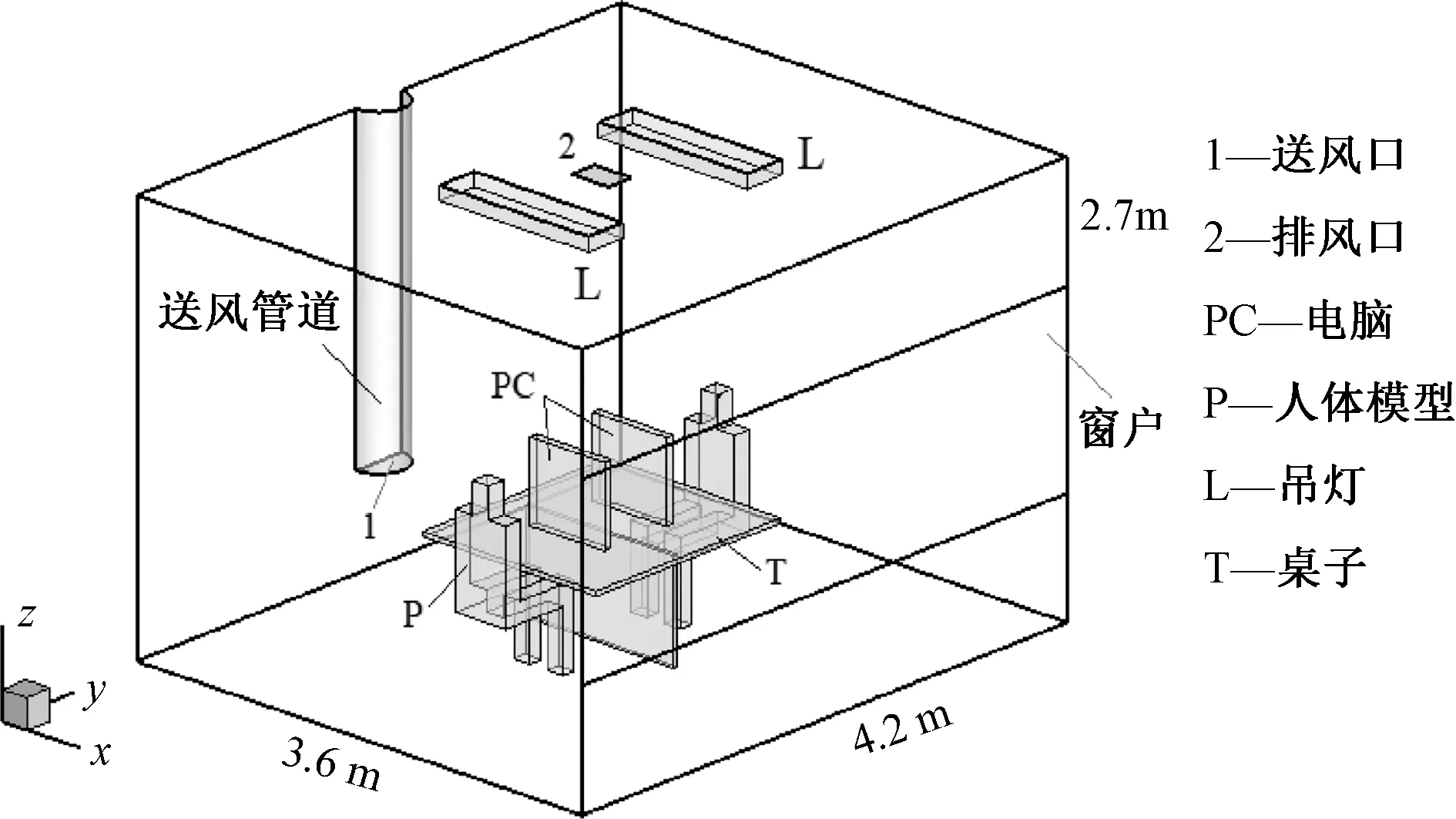
圖1 物理模型Fig.1 Physical model

室內包括兩個簡化的人體模型(均處于坐姿狀態)、兩臺電腦、一張桌子和兩盞吊燈，如圖1所示，其中，每個人體模型的散熱量為80 W，每盞吊燈的散熱量為36 W，每臺電腦的散熱量為100 W。由此可知，由內部熱源所引起的室內總冷負荷為432 W。模擬過程中認為，與所研究房間相鄰的房間均為空調房間，除外墻為熱損失面外，其他墻面(包括屋頂和地面)均設為絕熱面。外墻的邊界條件按第二類邊界條件處理，設為恒定熱流密度。對于表1所列不同工況，通過調整外墻的熱損失強度Qw使工作區(取為1.3 m以下空間)平均溫度維持在熱舒適狀態，即(25.0±0.3)℃。各個工況所對應的外墻熱損失強度Qw列于表1中。

1.2.2 數值計算方法

設室內空氣流動為三維連續、不可壓縮流，采用Reynolds時均N-S方程計算室內空氣的湍流流動，湍流模型選用RNGκ-ε兩方程模型。數值計算時，考慮到浮力的影響，空氣密度采用Boussinesq假設[13]，采用SIMPLE算法對壓力和速度項進行求解。關于模型的離散化，除壓力項采用標準Standard格式外，其他項均選用二階迎風格式。所有固體表面均設為無滲透和無滑移條件，送風口邊界類型設為velocity-inlet，并假定流速均勻，排風口邊界定義為outflow。

采用非結構化四面體網格劃分物理模型，并且對室內溫度和速度變化較快的熱源表面、送風口、回風口及近壁面等區域的網格進行加密處理。本研究中的最小網格尺寸為0.05 m，網格增長因子為1.15，最終所劃分的網格總數為311萬。

1.2.3 數學模型的合理性驗證

為驗證數值計算方法的合理性，采用與文獻[14]相同的邊界條件和室內熱源條件，對采用置換通風房間內的流場和溫度場進行數值模擬，并與文獻[14]給出的實測結果和模擬值進行對比。房間內共布置了9個測桿，測桿位置如圖2所示，具體試驗細節詳見文獻[14]。由于篇幅限制，僅給出3號和9號測桿溫度和速度的實測值和模擬值對比，如圖3所示。

圖2 測桿位置Fig.2 Locations of the nine measuring poles

圖3 溫度和速度的實測值與模擬值對比Fig.3 Comparison of the temperature and velocity distributions between the numerical results and experimental data

由圖3可知，本文的數值模擬結果和文獻[14]給出的數值結果均與實測值有一定的偏差。對于溫度分布，該偏差主要在近地面區域。對于速度分布，這一偏差主要集中在房間下部和頂部區域。造成這一現象的原因歸結如下：一方面，由于送風氣流被直接送至房間下部，導致近地面區域湍流強度波動明顯，而該區域的溫度和速度受湍流模型和離散格式的影響較大，從而帶來一定的計算偏差；另一方面，由于靠近地板和屋頂區域的氣流速度較小，熱線風速儀在測量低速度時存在一定的測量誤差。總體而言，溫度和速度的偏差均處于可接受范圍，并且對于多數測點，本文獲得的模擬結果與文獻[14]的模擬結果均與實測值能夠較好地吻合，由此可見本文的數值計算方法是合理可靠的。

2 結果與分析

2.1 田口分析法進行單目標優化

田口方法使用信噪比RS/N作為分析反應的特性值，以達到改善并尋求最優的設計目標。RS/N=平均數/變異數，其大小能夠同時反映每次試驗的平均值和偏差。信噪比分為望小特性、望目特性和望大特性，其中，望大特性希望質量特性值越大越好，望小特性則希望質量特性值越小越好。本文希望Δt、τbz和Dr越小越好，因此選用望小特性信噪比；希望η越大越好，故選用望大特性信噪比。望大特性和望小特性信噪比的計算公式[11]如式(1)和(2)所示。

望小特性：

(1)

望大特性：

(2)

式中：yi是第i組試驗所對應的試驗結果；n為試驗總次數，本研究中n=9。

利用上述數值模擬方法，對表1所列試驗工況的Δt、τbz、Dr和η等進行計算。利用Minitab 17.0軟件對處理后的數據進行主效應分析，通過對各項指標進行響應優化，得到各指標所對應的信噪比RS/N。表2給出了各指標的計算結果及所對應的信噪比RS/N。

表2 數值模擬結果及對應的信噪比Table 2 Numerical results and the corresponding signal-to-noise ratio

將各設計變量在不同水平下的信噪比計算平均值，可以得到設計變量對各指標的影響程度，并繪出設計變量信噪比平均值隨不同水平的變化圖。針對各項評價指標，設計變量在不同水平下的信噪比平均值變化趨勢如圖4所示。

在效應圖中，信噪比隨設計變量變化的斜率越大，則該變量對響應值的影響越顯著。由圖4可以看出:影響頭足溫差Δt的主效應因素為送風溫差Δts> 送風速度vs> 送風口高度h；而對于τbz、Dr和η，影響最大的設計變量均是送風速度vs，其他因素的影響均較小，且相差不大。

信噪比越大則表示一個系統的穩健性越好，代表該因素中此水平處理效果最佳。由圖4可知:對于Δt，最佳的設計變量組合條件為h2vs3Δts1；對于τbz，最佳的設計變量組合條件為h2vs3Δts2；對于Dr，最佳的設計變量組合條件為h1vs1Δts1；對于η，最佳的設計變量組合條件為h1vs1Δts2。

由以上分析可知，對于單個評價指標而言，產生最大信噪比所對應的因素水平條件為最優，但對于多個評價目標，某條件下某一指標產生較高信噪比的同時，可能對其他評價指標產生較低的信噪比。比如，送風溫差Δts對Δt的信噪比最大，但其對η的信噪比最小(見圖4)。

另外，對于不同的評價指標，所得到的最佳設計變量組合也是不同的。顯然，分開使用這些評價指標來衡量通風性能的優劣是不準確的，需要對這些指標進行綜合評估。田口方法僅適用于對單一目標的優化[11]，對于多個目標的優化需要借助其他手段。因此，將借助灰色關聯分析法實現多目標參數的優化。

2.2 灰色關聯分析的多目標優化

2.2.1 灰色關聯分析

灰色關聯分析通過計算目標變量的無量綱化數據序列和系統特征變量(灰色關聯系數)數據序列的灰色關聯度，將復雜的多目標優化問題轉化為僅對灰色關聯度的單目標優化[15]。在該方法中，首先，利用式(3)和(4)對原始目標變量進行無量綱化處理，結果見表3。然后，通過式(5)計算關聯系數。需要指出的是，在進行灰色關聯度計算之前，需要評估這4個指標之間的重要層級，即各指標的權重。本文采用熵度量法[16]對各目標變量的權重進行計算，結果發現，Δt、τbz、Dr及η所對應的權重分別為25.32%、24.86%、24.95%和24.87%，四者相差不大。因此，在計算灰色關聯度時忽略了權重對關聯度計算結果的影響[16]。最后利用式(5)對各目標變量的關聯度進行計算。表4給出了各評價指標的灰色關聯系數和關聯度的計算結果。

望大特性：

(3)

望小特性：

(4)

(5)

(6)

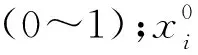
表3 各目標變量信噪比的標準化結果

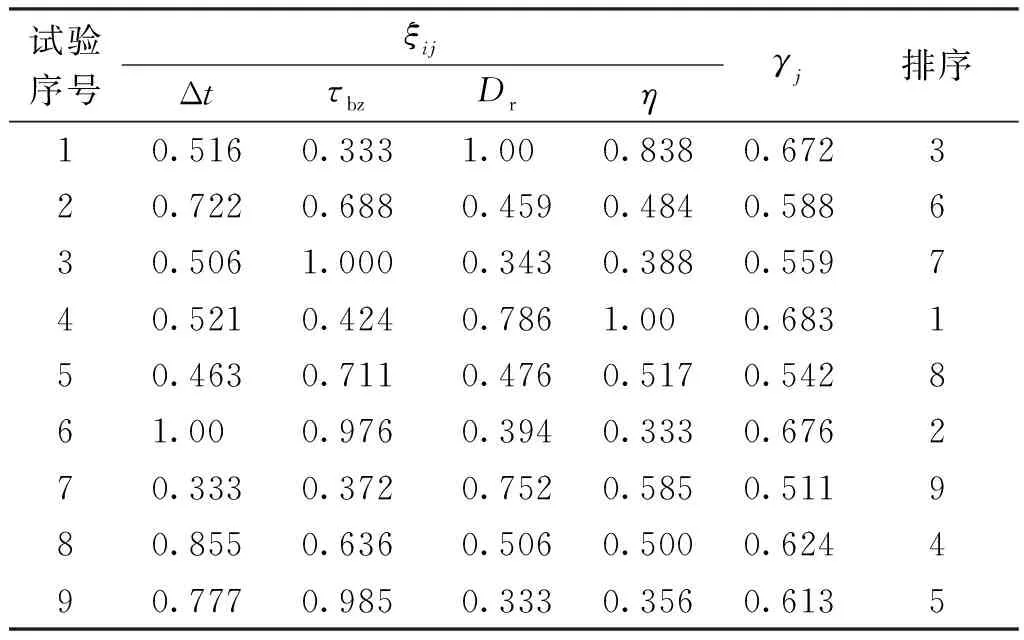
表4 各目標變量的灰色關聯系數及灰色關聯度

灰色關聯度數值越大，表明本組試驗值越接近理想值。由表4可知，第4個試驗的灰色關聯度最大，具有最好的綜合性能，其次為第6組和第1組試驗。各設計變量在不同水平下的灰色關聯度平均值的變化趨勢如圖5所示。

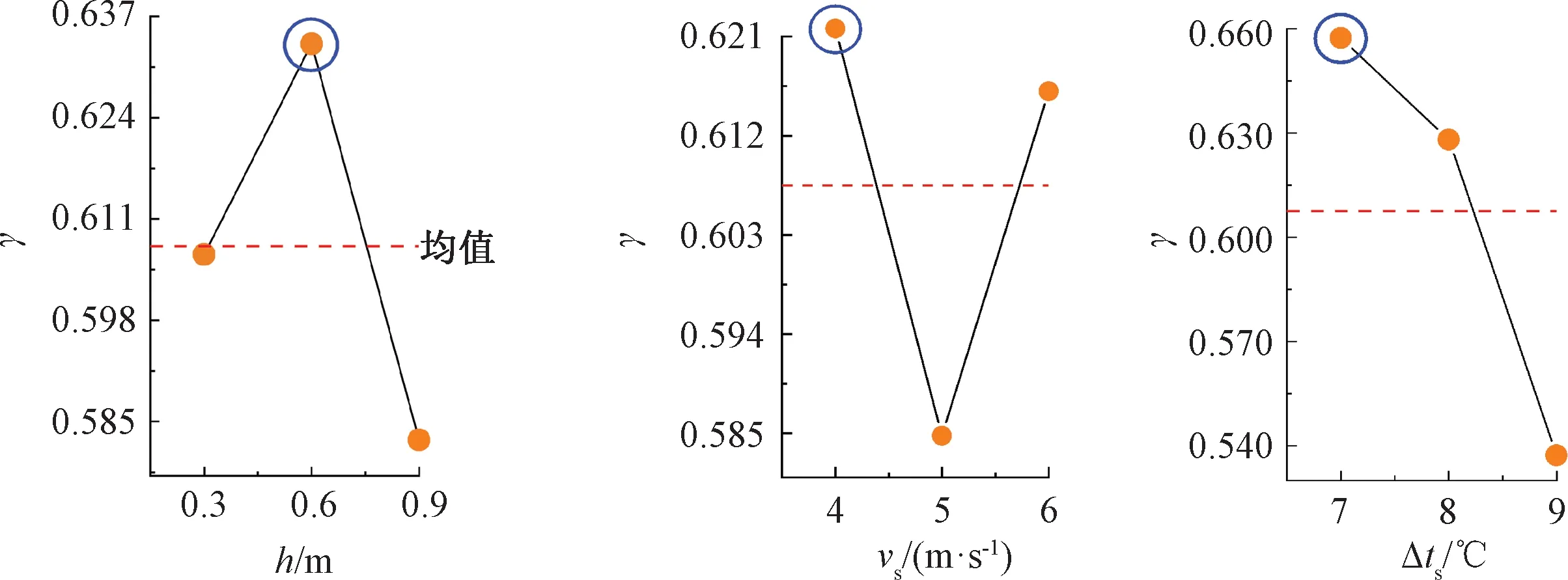
圖5 灰色關聯度平均值的變化趨勢Fig.5 Variation trend of the averaged gray relational grade

根據圖5可知，各因素對IJV整體通風性能的影響程度為Δts>h>vs。為了使灰色關聯度最大，h的2號水平、vs的1號水平、ts的1號水平為各因素的最佳水平。

2.2.2 方差分析

方差分析用于確定各設計變量對整體通風性能影響的顯著性。表5給出了灰色關聯度的方差分析結果。

F值是各因素影響顯著性的重要指標，F值越大，說明該因素的影響越顯著。由表5可知，對IJV的整體通風性能而言，Δts的影響最顯著，h和vs的影響小。從各影響因素的貢獻率可知，這3個影響因素都不可忽略。因此，可初步確定h=0.6 m，vs=1.2 m/s，Δts=2 ℃為最佳的設計變量組合。

表5 灰色關聯度的方差分析(置信水平：95%)Table 5 Analysis of variance of grey correlation degree (confidence level: 95%)

3 驗證試驗

由于所得到的最優設計變量組合(h2vs1Δts1)是正交表中沒有的方案，故需要做試驗予以驗證。原始試驗方案(h2vs1Δts2)與優化試驗方案所得到的試驗結果如表6所示。

表6 驗證試驗結果Table 6 Verify experimental results

由表6可知，優化試驗方案后，Δt和Dr均降低，η得到提高，雖然τbz增大了，但增大百分比非常小，可忽略不計。此外，在最優試驗方案下預測的灰色關聯度γ′j可由式(7)計算得出。

(7)

對驗證試驗的結果進行分析可知，驗證試驗的灰色關聯度為0.710，與利用式(7)預測的灰色關聯度γ′j非常接近，其相對誤差僅為3%，結果較為滿意。更重要的是，驗證試驗所得到的灰色關聯度比原有試驗中最大的灰色關聯度(0.683)還要高，這說明通過對信噪比的灰色關聯度進行分析，獲得了使通風性能更優的設計變量組合h2vs1Δts1。同時也說明灰色關聯分析法可用于空調送風系統通風性能的多目標優化，以獲得實現最佳通風效果所對應的設計變量組合條件。

4 結 語

利用田口方法的正交試驗設計和信噪比理論研究送風溫差、送風口高度、送風速度對IJV通風性能的影響，并利用灰色關聯分析法將復雜的多目標優化問題轉化為僅對灰色關聯度單一目標進行優化，得出以下主要結論：

(1)送風溫差對頭足溫差的影響最大，其次為送風速度和送風口高度，而在影響呼吸區空氣齡、吹風感和送風能量利用系數的各設計變量中，最大影響因素均是送風速度，其他因素的影響均較小，且相差不大。

(2)對于頭足溫差，最佳的設計變量組合條件為h2vs3Δts1；對于呼吸區空氣齡，最佳的設計變量組合條件為h2vs3Δts2；對于吹風感，最佳的設計變量組合條件為h1vs1Δts1；對于送風能量利用系數，最佳的設計變量組合條件為h1vs1Δts2。

(3)IJV整體通風性能達到最佳的設計變量組合條件為送風速度1.2 m/s、送風溫差2 ℃、送風口高度0.6 m。

研究結果對IJV的優化設計具有很強的指導作用，并且基于田口方法的灰色關聯分析法可為暖通空調領域所涉及的多目標優化問題提供新思路。