靜壓造型線伺服直驅泵控液壓系統設計*

王琳琳

(安徽冶金科技職業學院機械系，安徽 馬鞍山 243000)

引言

交流電機調速技術的迅猛發展，使伺服直驅泵控液壓系統的設計技術日趨成熟，該系統是融合伺服電機控制和容積控制兩種技術的新型傳動系統[1]，可以通過對伺服電機的調速、換向等功能，直接驅動定量泵進行方向和速度的切換，控制執行元件的壓力以及位置等，同時該系統具有集成度高、易于控制和高效節能等優勢[2].靜壓造型線作為一種自動鑄造設備，因具有成型效果好與自動化水平高等特點，已逐漸成為各鑄造廠的核心設備之一.近年來伺服直驅泵控液壓系統在靜壓造型線中獲得廣泛應用，系統的控制效果對保證靜壓造型線安全穩定運行起著重要作用，但由于系統控制的動態響應較慢[3-4]，導致伺服直驅泵控液壓系統對靜壓造型線的控制效果不理想，因此設計性能較好的靜壓造型線伺服直驅泵控液壓系統具有重要意義.

當前針對此類系統的設計成果有很多，例如魏秋紅等人[5]和楊可可等人[6]，分別使用分數階控制器以及魯棒H∞控制，實現靜壓造型線伺服直驅泵控液壓系統設計.雖然以上兩種系統的動態特性明顯改善，且能量消耗較少，但對負載干擾和參數攝動的抑制能力較差.為解決以上研究存在的問題，本文以小波神經網絡控制器為核心設計靜壓造型線伺服直驅泵控液壓系統，以進一步提升系統的控制性能，為靜壓造型線的順利運行提供更好的保障.

1 靜壓造型線伺服直驅泵控液壓系統

1.1 靜壓造型線伺服直驅泵控液壓系統結構

靜壓造型線伺服直驅泵控液壓系統包含計算機控制部分、伺服調速部分以及液壓動力機構，系統具體結構如圖1所示.

圖1 靜壓造型線伺服直驅泵控液壓系統結構

信號采集反饋模塊使用壓縮感知方法獲取靜壓造型線內液壓缸的壓力和位置信號，將其傳輸到計算機控制部分的主控制器進行比較處理，運用D/A數模轉換模塊轉化信號處理結果，使其變為控制信號，并傳送到伺服調速部分的電動機控制器[7]，其控制電動機直接驅動定量泵執行方向和速度的切換，以達到控制靜壓造型線內液壓缸的目的.該系統屬于閉環控制系統，可以依據返回的信號值實時調整伺服電機，以滿足負載變化的需求.

1.2 基于壓縮感知的信號采集方法

假設長度有限且維數為n的信號用x表示，若想表明x在某個矩陣ψ上具有稀疏性，則該矩陣應滿足公式(1)所示表達式：

x=ψz,‖z‖0=k

(1)

式(1)中，原始信號用x表示；稀疏向量用z表示，且滿足x,z∈Rn×1；稀疏矩陣用ψ表示，且滿足ψ∈Rn×n；稀疏度用k表示；向量z的l0范數用‖z‖0表示.

假設測量矩陣用φ表示，在該矩陣內滿足條件y=φx的情況下，通過公式(2)所示關于l0范數的最優化問題的求解，可以實現x的高概率重構，重構方式以及重構誤差的計算過程如公式(3)、(4)所示：

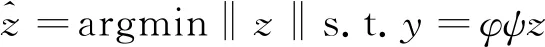
(2)

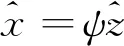
(3)

(4)

依據上述壓縮感知理論可得，用x代表靜壓造型線內液壓缸的壓力和位置原始信號，且φ為隨機矩陣的情況下，可認為y=φx表示對壓力與位置信號進行隨機采樣[8-9].因為測量向量維數m的值比信號維數n的值小，所以在靜壓造型線內液壓缸的壓力和位置信號采集過程中還實現了信號數據壓縮[10]，對降低信號采樣頻率以及提高后續信號轉換效果具有重要作用.下述為所選用加性隨機采樣方法的具體過程.

步驟一：依據靜壓造型線內液壓缸的壓力和位置信號特點、矩陣維數以及信號重構精度等因素，運用下式對采樣時間窗進行計算：

Tw=n/fs

(5)

式(5)中，采樣時間窗用Tw表示，單位為s；采樣頻率用fs表示，單位為Hz.每個采樣時刻值的計算過程如公式(6)所示：

ti=ti-1+τi

(6)

式(6)中，次序為i的采樣時刻用ti表示，其中i的取值介于[1,α]范圍內，采樣時刻間隔用τi表示.

步驟二：當τi屬于高斯隨機數時，通過上式獲得采樣時刻序列，因此可得到公式(7)所示結果：

τi=(Aa,Bb)+s×N(0,1)

(7)

式(7)中，收斂因子用(Aa,Bb)表示；時間變動因子用s表示；高斯隨機變量用N(0,1)表示.

1.3 小波神經網絡控制器設計

由于負載擾動、流量脈動以及電氣參數等對靜壓造型線伺服直驅泵控液壓系統的性能具有較大影響[11-13]，因此可以利用精準識別異常信號的小波神經網絡，實現伺服直驅泵控液壓系統對靜壓造型線內液壓缸的壓力與位置的雙閉環控制.

小波神經網絡控制器的網絡結構包含輸入層、隱含層和輸出層.通過歸一化處理輸入信號樣本[14,15]，將處理結果傳輸到隱含層，該層利用選取的小波函數處理接收到的信號樣本，并傳送到輸出層，比較真實輸出結果和期望值，運用兩者的差值反向訓練小波神經網絡每個層級的連接權值，重復以上過程，停止條件為網絡的全局平方和滿足提前預設的精度.

1.3.1 小波神經網絡結構及其算法

假設函數空間用L2(R)表示，根據離散小波變換原則，如果給定函數滿足ψ(t)∈L2(R)，且符合公式(8)所示約束條件，則稱ψ(t)為基小波函數.

(8)

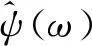
(9)

式(9)中，尺度因子用a表示，平移因子用b表示，a和b滿足a,b∈R，且a的值不等于0.

依據以上理論可獲得如圖2所示的小波神經網絡結構.

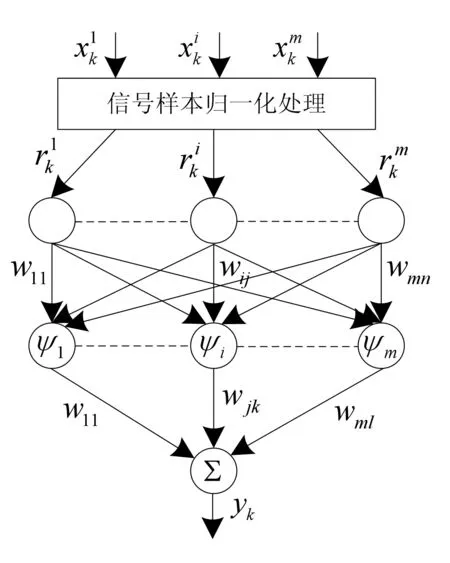
圖2 小波神經網絡結構圖

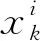
(10)

式(10)中，隱含層小波函數用ψj(x)表示.

1.3.2 小波神經網絡控制器設計過程

步驟一：歸一化信號樣本.將采集的靜壓造型線內液壓缸的壓力和位置信號作為網絡的輸入信號樣本，由于不同信號樣本的取值范圍具有較大差異，需要使用下式歸一化處理信號樣本，以避免網絡訓練過程中陷入局部極值.

(11)

式(11)中，信號樣本最大值用xmax表示，最小值用xmin表示.

步驟二：初始化小波神經網絡.以隨機形式對aj、bj以及網絡連接權值ω進行初始化，并將學習速率設定為0.1，動量因子設定為0.06.

步驟三：控制輸出.將輸入信號樣本劃分為訓練和測試樣本兩部分，將訓練樣本作為網絡輸入，在獲得網絡控制輸出的基礎上，對其與期望輸出之間的誤差E進行計算.

步驟四：權值更新.將E作為依據更新小波函數參數和網絡權值，使控制輸出結果不斷接近期望結果.

2 結果分析

以某鑄造廠的靜壓造型線作為實驗對象，在AMESIM仿真環境下，依據本文設計的伺服直驅泵控液壓系統，搭建完整的系統模型，該模型的公式為：

(12)

通過該模型對靜壓造型線內液壓缸的壓力和位置信號進行采集，并實現相應的控制功能，同時增加負載力干擾，將仿真時間設置成12 s.

使用本文系統采集的靜壓造型線內液壓缸的壓力和位置信號，如圖3所示.

(a)液壓缸壓力信號波形圖

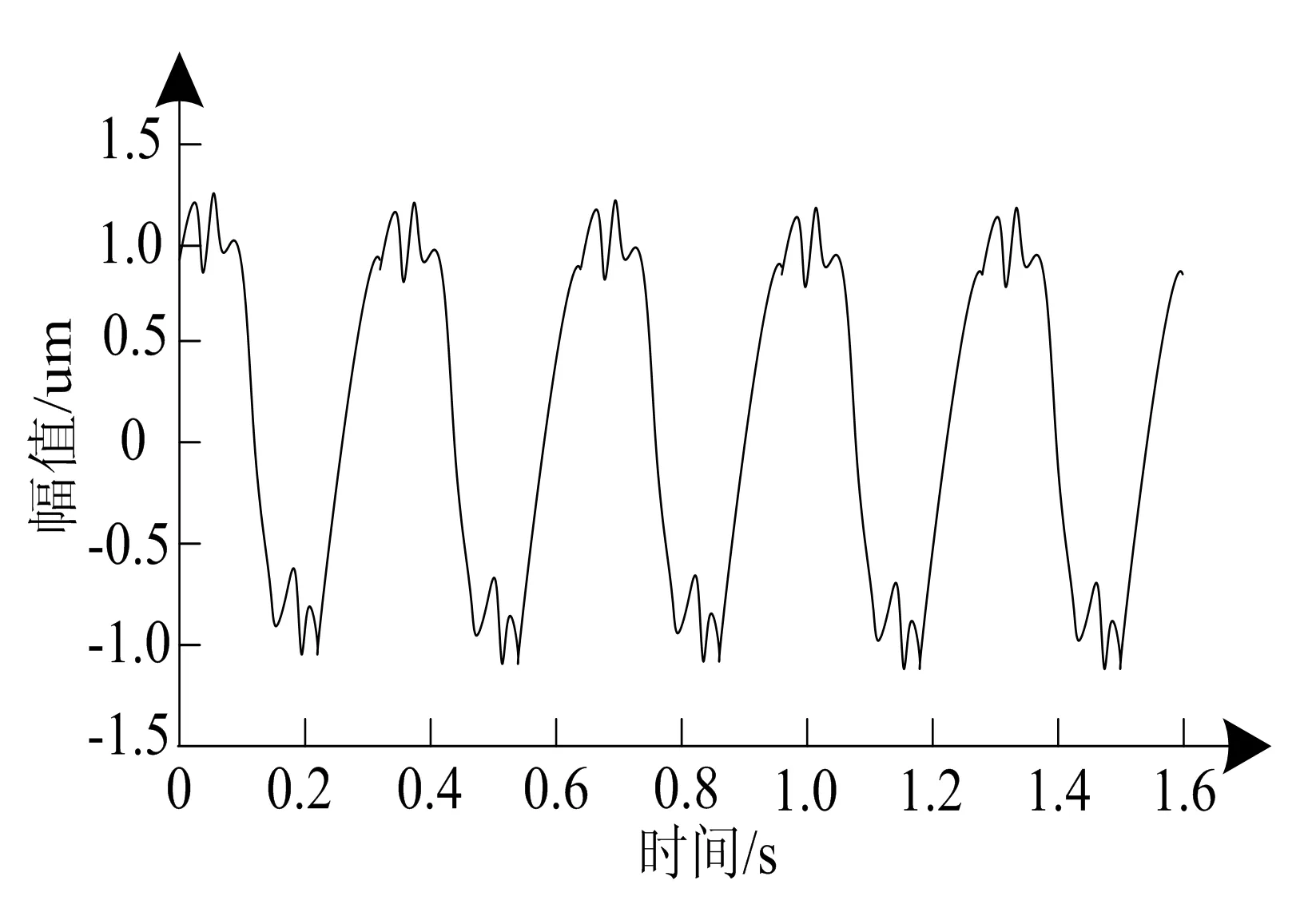
(b)液壓缸位置信號波形圖

分析圖3可以看出，本文系統具有良好的靜壓造型線內液壓缸的壓力和位置信號采集效果，所得信號波形完整連續，且不存在噪聲，能有效反映不同類型信號特點，有助于提升后續伺服直驅泵控液壓系統對靜壓造型線的控制精度.

當伺服直驅泵控液壓系統存在不同程度的負載力干擾時，獲得的靜壓造型線內液壓缸A和液壓缸B的位移跟蹤響應結果，如圖4所示.

圖4 不同液壓缸的位移跟蹤響應結果

分析圖4可以發現，當伺服直驅泵控液壓系統的負載力干擾小于2 000 N時，靜壓造型線內液壓缸A和液壓缸B的實際位移和期望位移基本一致；當負載力干擾大于2 000 N時，兩個液壓缸的實際位移開始偏離期望位移，但兩者之間的差值很小.

因此表明，本文系統能很好地控制靜壓造型線內液壓缸的位置，并且在系統具有較大負載力干擾的情況下，仍能表現出較理想的控制性能.究其原因是本文系統設計的包含輸入層、隱含層和輸出層的小波神經網絡控制器網絡結構，可以精準識別異常信號的小波神經網絡，實現伺服直驅泵控液壓系統對靜壓造型線內液壓缸的壓力與位置的雙閉環控制，一定程度上有利于提高控制能力.

本文系統使用后，獲得的靜壓造型線內液壓缸兩個端口的壓力響應曲線，如圖5所示.

圖5 內液壓缸兩個端口的壓力響應曲線

分析圖5可以發現，使用本文系統對靜壓造型線內液壓缸的壓力進行控制后，液壓缸兩個端口的壓力響應均在0.4 s達到穩定狀態，在達到穩態之前，端口2的壓力響應速度更快.因此可得，本文系統具有較理想的靜壓造型線內液壓缸的壓力控制效果，可以使液壓缸不同端口的壓力迅速穩定下來，響應快速性較為優良.

靜壓造型線的運行過程，主要包括工作行程、保壓階段、快速回程以及待機階段四種狀態，測試不同伺服電機轉速下，靜壓造型線處于不同狀態時的平均功率，結果如表1所示.

表1 靜壓造型線不同狀態時的平均功率

分析表1可以得出，隨著伺服電機轉速持續增加，靜壓造型線處于不同狀態時的平均功率均呈現出先緩慢上升，并在伺服電機轉速達到1 600 rmp時開始趨于穩定的態勢；當靜壓造型線處于快速回程狀態時，不同伺服電機轉速下的平均功率始終保持最高，最大值為61.5×103kW；當靜壓造型線處于待機狀態時，伺服電機停止轉動，平均功率為0.以上結果可得，伺服電機轉速對靜壓造型線運行過程中的能量消耗具有一定影響，但在伺服電機轉速達到某個數值時，不會再過度消耗能量，表明本文系統通過控制可有效保證靜壓造型線的節能效果.

3 結論

伺服直驅泵控液壓系統的控制效果直接關系著靜壓造型線的安全穩定運行，因此本文設計的靜壓造型線伺服直驅泵控液壓系統，通過對靜壓造型線內液壓缸的壓力和位置控制，保證靜壓造型線能夠順利完成鑄造任務.經過仿真分析可知，該系統可以采集到質量較高的液壓缸壓力和位置信號，且利用小波神經網絡控制器能很好地控制液壓缸的壓力和位置，同時該系統能有效保證靜壓造型線的節能效果，對促進鑄造廠的自動化發展具有重要參考價值.