繩牽連問題中加速度關系的求解

段石峰

(湖南省長沙市周南中學，湖南 長沙 410201)

1 繩牽連問題中的加速度關系

例：如圖1所示，圓環套在固定豎直桿上，用輕繩連接后跨過輕質定滑輪與物塊相連，開始時圓環與滑輪等高。桿與滑輪間的距離為l，繩和桿足夠長，不計一切阻力。現將圓環由靜止釋放，求圓環加速度a1和物塊加速度a2之間滿足的關系式。

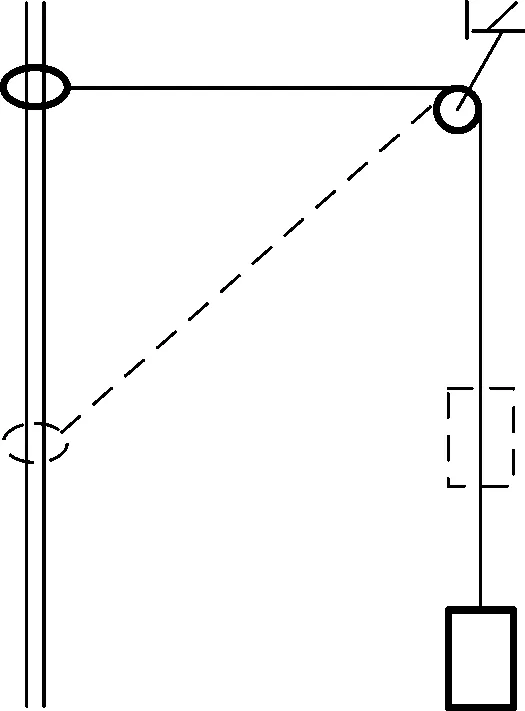
圖1

分析：如圖2所示，設圓環下降到某一位置時繩與水平方向的夾角為θ，圓環和物塊的速度分別為v1和v2，將圓環的速度v1分別沿繩方向和垂直繩方向進行正交分解，由于繩不可伸長，圓環和物塊沿繩方向的速度大小相等，有：v2=v1sinθ。

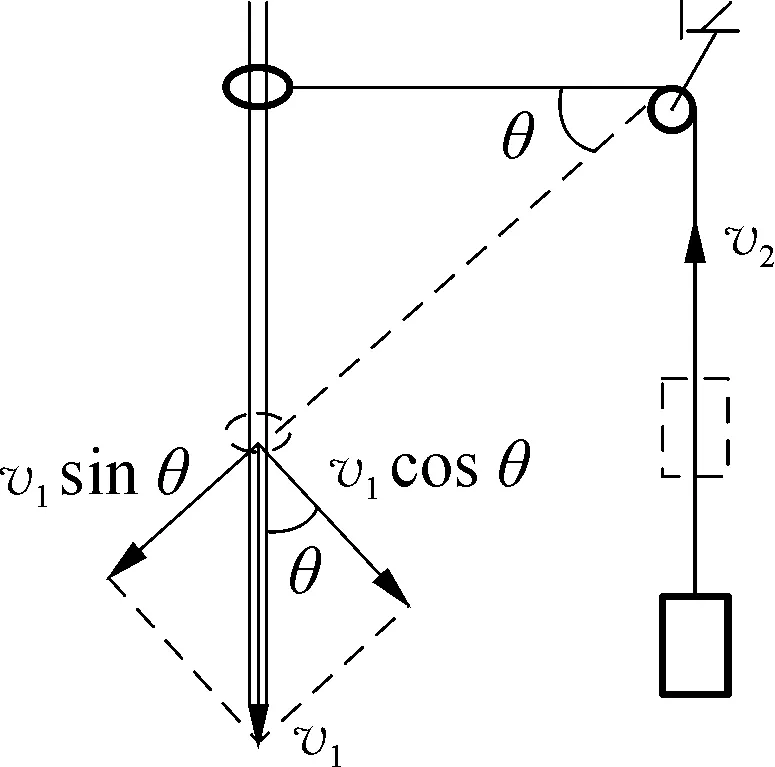
圖2

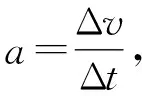
1.1 矢量圖解法

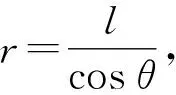
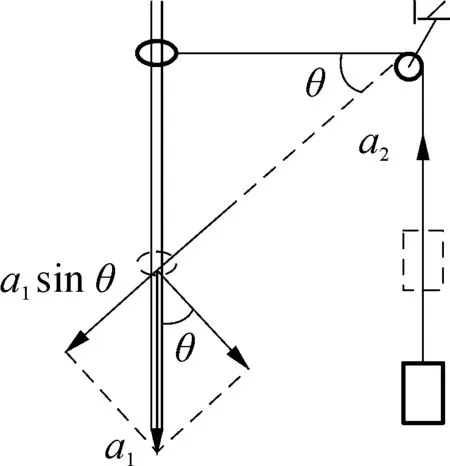
圖3

1.2 數學求導法

1.2.1 對速度關系式求導

1.2.2 對幾何關系式求導

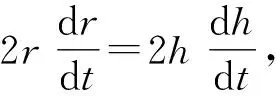
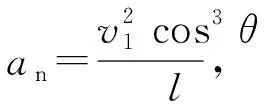
2 求解繩牽連問題中的的最大速度

在上述問題中，若已知圓環的質量m1=3 kg，物塊的質量m2=5 kg，桿與滑輪間的距離l=2 m，重力加速度取g=10 m/s2，求圓環和物塊的最大速度。

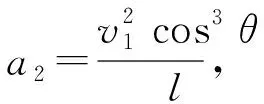
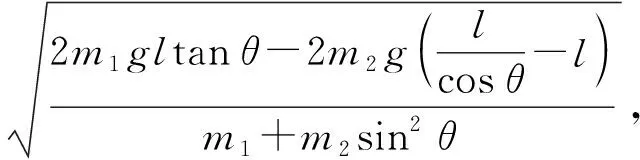
對其求導并令導數為0，也可進行求解，但難度也較大。筆者利用《幾何畫板》軟件繪制出函數圖像，以求出數值解，如圖4所示，實線為v1-θ圖像，虛線為v2-θ圖像。由圖4可知：當θ≈0.471 rad≈26.99°時，圓環的最大速度約為3.017 m/s；當θ≈0.781 rad≈44.75°時，物塊的最大速度約為1.838 m/s。

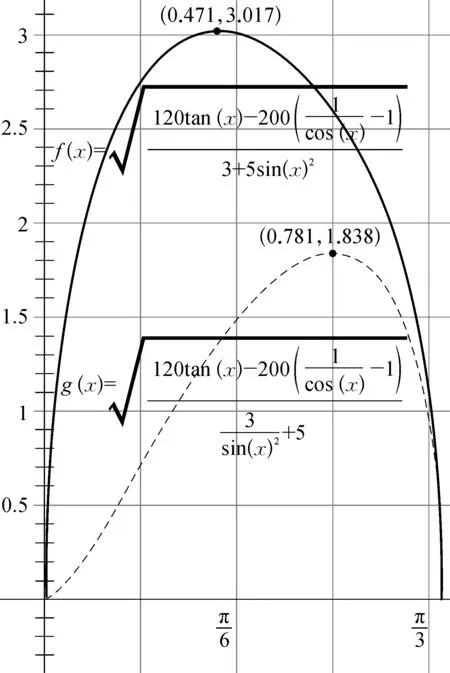
圖4

3 結語

繩牽連和桿牽連問題中的加速度關系具有類似的特點，不僅要考慮加速度矢量的分解，還要考慮由于轉動而引起的向心加速度。當然，高中物理不要求定量求解加速度大小不同的連接體問題，一般地不要求學生掌握，因此在常規教學中應該盡量回避。但沒有超出高中學生的能力范圍，對于學有余力的學生，可以先采用矢量圖解法進行定性分析，再采用數學求導法進行定量計算。