一道2022年高考題的推廣

李院德

(安徽省教育科學研究院)

筆者受2022年全國新高考Ⅰ卷第12題的啟發(fā),證明了連續(xù)周期函數(shù)的導函數(shù)也是周期函數(shù),探究了其原函數(shù)也是周期函數(shù)的一個充要條件.本文通過幾個例子對這兩個定理進行進一步說明,并在此基礎(chǔ)上給出了幾點啟示.

1 問題的提出

在本題中,函數(shù)g(x)為函數(shù)f(x)的導函數(shù),通過推理我們不難發(fā)現(xiàn)函數(shù)g(x)和f(x)均為周期函數(shù),并且周期相同.眾所周知,函數(shù)f(x)＝cosx與其原函數(shù)F(x)＝∫cosxdx＝sinx＋c均是周期為2π的函數(shù),那么一個函數(shù)與其原函數(shù)周期的這種關(guān)系是否具有一般性呢?

2 連續(xù)函數(shù)與其導函數(shù)、原函數(shù)周期性之間的關(guān)系探究

2.1 周期函數(shù)的定義

設f(x)是定義在數(shù)集M上的函數(shù),如果存在非零常數(shù)T具有性質(zhì):f(x＋T)＝f(x),則稱f(x)是數(shù)集M上的周期函數(shù),常數(shù)T稱為f(x)的一個周期.如果在所有正周期中有一個最小的,則稱它是函數(shù)f(x)的最小正周期.

注 由周期函數(shù)的定義不難發(fā)現(xiàn):

1)周期函數(shù)的定義域不必是一個連續(xù)區(qū)間,如f(x)＝1(x∈Z)是一個最小正周期為1的函數(shù),它的定義域是整數(shù)集.

2)周期函數(shù)的周期T可以是負值,且周期函數(shù)未必有最小正周期,如常數(shù)函數(shù)是以任何非零實數(shù)為周

2.2 連續(xù)函數(shù)與其導函數(shù)的關(guān)系

定理1 已知f(x)是定義在數(shù)集M上的周期為T的函數(shù),且處處可導,導函數(shù)為f′(x),則f′(x)也是周期為T的函數(shù).

證明 由于函數(shù)f(x)是定義在數(shù)集M上的周期為T的函數(shù),則有f(x＋T)＝f(x),又f(x)處處可導,則有

故導函數(shù)f′(x)也是周期為T的函數(shù).

2.3 連續(xù)函數(shù)與其原函數(shù)的關(guān)系

對于一個定義在某區(qū)間的已知函數(shù)f(x),如果存在可導函數(shù)F(x),使得在該區(qū)間內(nèi)的任一點都存在F′(x)＝f(x),則在該區(qū)間內(nèi)就稱函數(shù)F(x)為函數(shù)f(x)的一個原函數(shù).

由定理1,若一個可導函數(shù)為周期函數(shù),則其導函數(shù)也必然是周期函數(shù).然而,連續(xù)周期函數(shù)的原函數(shù)卻未必是周期函數(shù),如函數(shù)f(x)＝cosx＋1(x∈R),其原函數(shù)為F(x)＝sinx＋x＋c就不是周期函數(shù),其圖像如圖1所示.

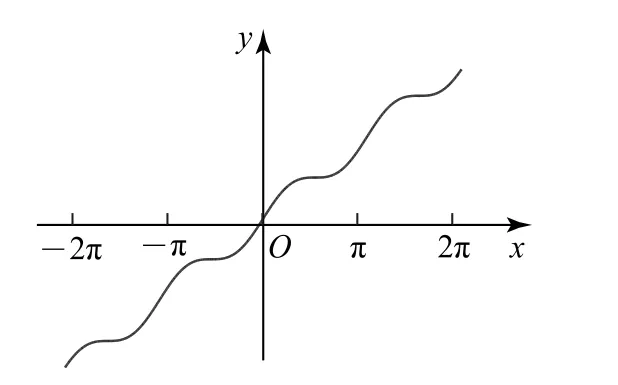
圖1

現(xiàn)在我們來探究使得連續(xù)周期函數(shù)的原函數(shù)是周期函數(shù)的條件.

定理2 已知函數(shù)f(x)是定義在數(shù)集M上的周期為T的函數(shù),且處處連續(xù),則其原函數(shù)F(x)也是周期為T的函數(shù)的充要條件是存在一個點x0∈M使得F(x0＋T)＝F(x0).

證明 必要性顯然成立,現(xiàn)證明充分性.

由于F(x)是函數(shù)f(x)的原函數(shù),則對任意x∈M有

因此F(x＋T)＝F(x),所以原函數(shù)F(x)是周期為T的函數(shù).

注 定理1揭示了可導的周期函數(shù)其導函數(shù)也一定是周期函數(shù),而定理2本質(zhì)上是給出了定理1的逆定理也成立的一個充要條件.

3 原題回顧

定理2的優(yōu)勢在于可操作性強,便于運用,學生只需要根據(jù)導函數(shù)的周期性,結(jié)合兩個點的函數(shù)值相等便能夠判斷其原函數(shù)也是周期函數(shù).下面運用定理解決2022年全國新高考Ⅰ卷選擇題第12題.

綜上,選BC.

根據(jù)題目條件能推導出g(x)是周期為2的函數(shù),運用定理2可以快速證明f(x)也是周期為2的函數(shù),在此基礎(chǔ)上容易判斷出本題各選項的正誤.

推論 已知函數(shù)f(x)是定義在數(shù)集M上的周期為T的函數(shù),且處處連續(xù),若原函數(shù)F(x)存在一條對稱軸,則F(x)也是周期為T的函數(shù).

4 幾個例子

定理1和定理2分別證明了連續(xù)周期函數(shù)的導函數(shù)與其原函數(shù)的周期性之間的關(guān)系.下面將通過幾個例子對這兩個定理做進一步說明.

例1 已知函數(shù)f(x)＝|x－2k|,x∈[2k－1,2k＋1),試判斷其導函數(shù)的周期性.

根據(jù)周期函數(shù)的定義,函數(shù)f(x)是周期為2的函數(shù),函數(shù)f(x)的圖像如圖2所示.

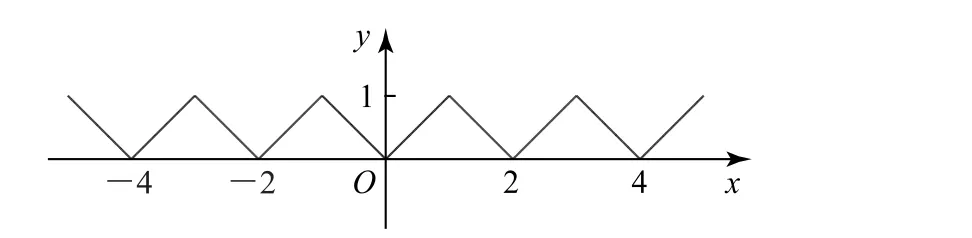
雖然函數(shù)f(x)是連續(xù)的,但在整數(shù)點上其導數(shù)都不存在.對任意的x∈R,x?Z,有

圖3

顯然函數(shù)f(x)在整數(shù)點上不連續(xù),因此在整數(shù)點上函數(shù)的導數(shù)都不存在.對于任意點x∈R,x?Z,有f′(x)＝1,易得f′(x)是周期為1的函數(shù).

例1中函數(shù)f(x)為連續(xù)函數(shù),且?guī)缀跆幪幙蓪?除整數(shù)點上導數(shù)不存在以外),該函數(shù)的導函數(shù)仍然為周期函數(shù).而對于例2,函數(shù)f(x)在整數(shù)點上不連續(xù),其他點處均連續(xù)且可導,其導函數(shù)也為周期函數(shù).因此,由例1和例2不難發(fā)現(xiàn),存在一些點不可導甚至不連續(xù)的函數(shù),但其導函數(shù)仍然保持了周期性.因此定理1中的條件并不是必要條件,可以進行弱化.

例3 已知函數(shù)f(x)＝cosx的定義域為R,試判斷其原函數(shù)是否為周期函數(shù).

圖4

5 啟示

5.1 數(shù)學教學要注重概念教學,突出數(shù)學本質(zhì)

5.2 數(shù)學教學要關(guān)注過程性和綜合性,提高學生發(fā)現(xiàn)問題、解決問題的能力

在知識的交會點設計試題是高考命題的一個立足點.本題的另一個特色是原函數(shù)f(x)與它的導函數(shù)g(x)互相聯(lián)系,又結(jié)合了函數(shù)的相關(guān)性質(zhì),特別是周期性與對稱性,綜合程度非常高.如此巧妙的綜合立意新穎,需要學生具備更高的問題解決能力,所以我們在教學中要適當關(guān)注問題與知識的綜合性,引導學生進行一些較為深入的探究.這樣我們的課堂才顯得有深度、有內(nèi)涵,引人入勝.尤其是在高中數(shù)學教學的后期,學生已經(jīng)具備了相關(guān)知識和能力,如果再一味刷題、機械重復,勢必會扼殺學生發(fā)現(xiàn)新問題、探索新思路的創(chuàng)新思維和能力.本題為高中一線教學特別是后期的復習課堂設計提供了很好的素材,也為探究課堂提質(zhì)增效的具體實施起到了很好的引領(lǐng)作用.因此,教師在教學中要注重知識之間的內(nèi)在聯(lián)系和發(fā)生發(fā)展過程,幫助學生構(gòu)建知識網(wǎng)絡,要重視學生探究能力的提升,引導學生從特殊到一般發(fā)現(xiàn)和提出問題,發(fā)展思維水平,培養(yǎng)創(chuàng)新意識和創(chuàng)新能力,培養(yǎng)學生綜合運用數(shù)學知識靈活解決問題的能力.

5.3 數(shù)學教學要關(guān)注差異性和層次性,促進不同數(shù)學水平的學生都能有所發(fā)展

2022年高考全國卷對周期函數(shù)進行了重點考查,幾套試卷中的相關(guān)題目都有一定的難度.周期函數(shù)是高中數(shù)學學習的重要內(nèi)容之一,在高中數(shù)學課程的學習中,學生學習了周期函數(shù)的概念,并重點學習了三角函數(shù)這一特殊周期函數(shù)的圖像和性質(zhì).教材通過從特殊到一般的編排形式幫助學生進一步加深了對周期函數(shù)及其性質(zhì)的理解.通過學習,學生能夠正確理解三角函數(shù)的圖像、性質(zhì)及其之間的聯(lián)系與區(qū)別.在一元函數(shù)的導數(shù)及其應用的學習中,學生又學習了正弦函數(shù)與余弦函數(shù)的導函數(shù),進一步加深了對正弦函數(shù)、余弦函數(shù)之間關(guān)系的理解.在高中選修課程中,?普通高中數(shù)學課程標準(2017年版2020年修訂)?又將微積分的基礎(chǔ)知識作為高中數(shù)學A 類課程和B類課程的重點內(nèi)容,通過學習選修課程,學生能理解微分和積分之間的關(guān)系.這些內(nèi)容的學習,為學生理解周期函數(shù)與其導函數(shù)及其原函數(shù)的關(guān)系提供了可能.對于這道題目,大部分學生利用高中數(shù)學知識通過數(shù)學推理發(fā)現(xiàn)兩函數(shù)的關(guān)系,進而解決問題,還有些學生利用特殊法代入數(shù)值進行計算,進而選擇出正確答案.因此,這道高考題很好地為不同程度的學生提供了不同解決問題的途徑,真正體現(xiàn)了高中數(shù)學課理念:實現(xiàn)每個學生都能獲得良好的數(shù)學教育、不同的學生在數(shù)學上得到不同的發(fā)展.

因此,教師在教學中要落實課程標準的理念和要求,注重將因材施教和面向全體相結(jié)合,根據(jù)學情、校情的實際開好必修、選擇性必修和選修課程,努力讓不同的學生都能得到發(fā)展.同時,教師應重視自身專業(yè)的學習,站在更高的高度理解數(shù)學知識,深入淺出地開展課堂教學,注重循循善誘,促進教學相長,不斷提升課堂教學的效果,真正使得學生的核心素養(yǎng)得到提升和發(fā)展.