慣性張量平移和旋轉復合變換的一般形式及其應用

黎 旭, 陳強洪, 甄文強, 王 碩

(中國工程物理研究院總體工程研究所，綿陽 621999)

0 引言

在汽車等領域的工程設計中，由于各組件慣性矩和慣性積參考系、安裝位置和姿態各不相同，常常需要將復雜系統不同組件的慣性矩(轉動慣量)、慣性積進行變換后合成[1–3]。特別是像運載火箭的質量特性隨時間變化的情況下，實現飛行軌跡計算時需要對慣性張量進行合成，現有方法主要是通過實物測量和CAD 模型測量獲得合成的慣性矩和慣性積。實物測量對測量設備要求較高，周期和成本也較高；CAD 模型測量需要建立完整的三維模型并賦相應的密度，只能對靜態模型進行合成，無法對慣性矩和慣性積進行快速合成。

為實現隨時間變化的不同剛體組件慣性矩和慣性積的快速合成，需要對其進行坐標變換，已有文獻給出了剛體慣性矩和慣性積分別進行平移或旋轉變換的形式[4–7]，但缺少平移、旋轉復合變換的一般形式。本文首先從慣性張量的基本定義出發，采用矩陣變換導出了一般的慣性張量分量矩陣平移和旋轉變換關系，然后將不同坐標系下的組件慣性張量變換到同一坐標系下，最后直接疊加實現慣性矩和慣性積的快速合成，方法具有一定理論意義和工程使用價值。

1 慣性矩、慣性積與慣性張量的描述

慣性張量是描述剛體做定點轉動的物理量，包含慣性矩和慣性積信息[8]。為了描述慣性張量，定義直角坐標系O ?xyz(S)，x、y、z方向的基元分別為i、j、k，則剛體上任意一點的位置矢量可表示為

其中u為剛體上任意一點的位置矢量，f為坐標系S的基元構成的矢陣(f=[i,j,k]T)，r為u在S中的坐標(r=[x,y,z]T)。

剛體的慣性張量定義為[3]

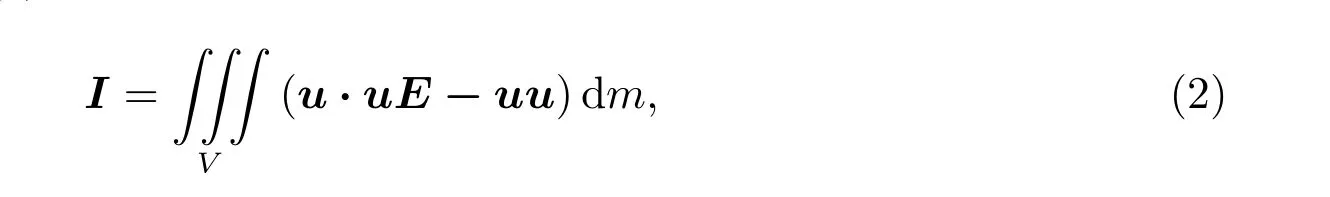
其中I為剛體慣性張量，u為剛體上任意一點的位置矢量，u · u為內積，uu為并矢，E為單位張量。

由式(1)和式(2)，可得

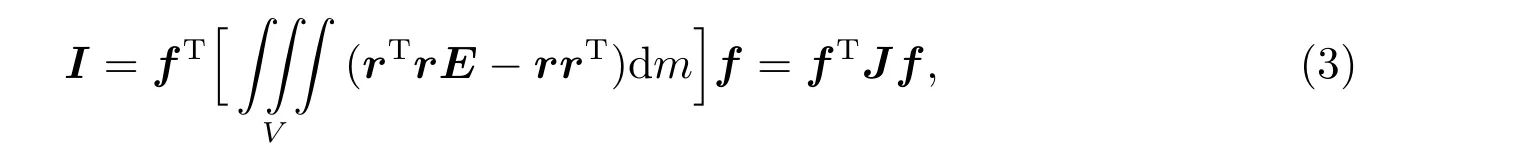
其中J為慣性張量I在S中的分量矩陣(慣性矩陣)[3,7–8]，形式為

其中Jxx為相對x軸的慣性矩，Jyy為剛體相對y軸的慣性矩，Jzz為剛體相對z軸的慣性矩，Jxy為剛體相對x、y軸的慣性積，Jyz為剛體相對y、z軸的慣性積，Jzx為剛體相對z、x軸的慣性積，其中Jzx=Jxz。

2 慣性張量平移和旋轉變換的一般關系

2.1 位置矢量的坐標變換關系

為了將局部坐標系下的慣性張量分量矩陣變換到全局坐標系下，首先需要知道局部坐標系與全局坐標系的坐標變換關系。構造如圖1 所示的兩個坐標系，O1x1y1z1(S1)為局部坐標系，O2x2y2z2(S2)為全局坐標系。O1相對于O2的位置矢量為u0，在S2中的坐標為r0。剛體上任一點A相對于O1的位置矢量為u1，在S1中的坐標為r1。A相對于O2的位置矢量為u2，在S2中的坐標為r2，剛體在S1下的質心坐標為rC。

由圖1 中的幾何關系可得

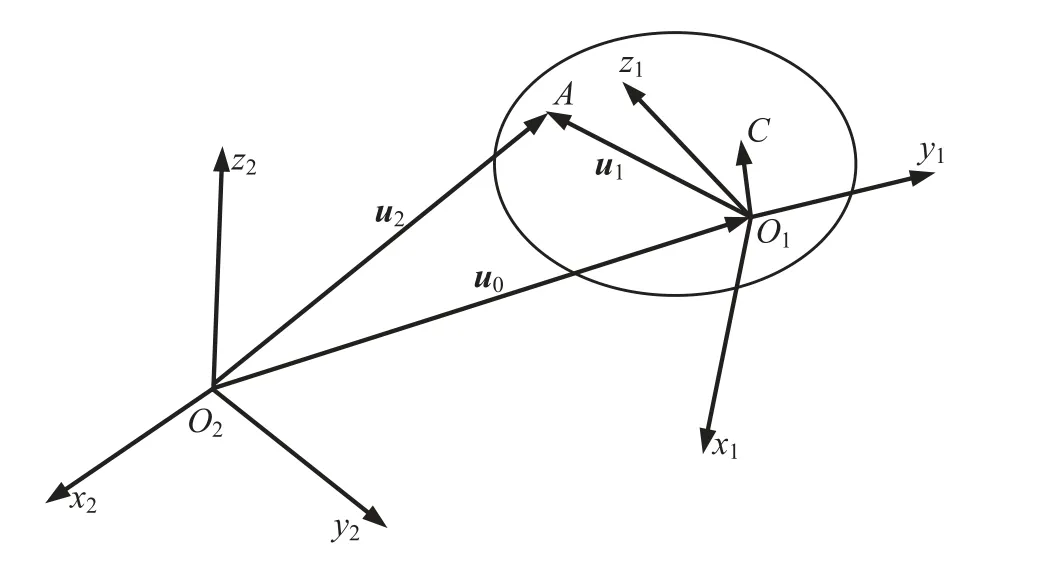
圖1 剛體的坐標變換關系

寫成坐標系下的形式為

由S2的基元矢陣f2通過基元旋轉，可得到S1的基元矢陣

其中L為旋轉矩陣，同時也是正交矩陣。任何兩個坐標軸不平行的坐標系可以通過若干次基元旋轉變成各軸互相平行的坐標系，這里按照z ?y ?x的順序(也可以其它順序)旋轉f2至與f1平行，通過三次如圖2 所示的Euler 角基元旋轉實現。

圖2 坐標系的基元變換

旋轉變換矩陣為

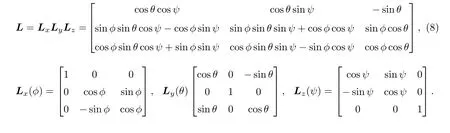
式(7)帶入式(6)，可得包含平移和旋轉的坐標變換關系

2.2 慣性張量分量矩陣的變換關系

得到剛體位置矢量的坐標變換關系后，下面考慮坐標變換下的張量矩陣關系。由式(4)可知，全局坐標系S2下的慣性張量分量矩陣為

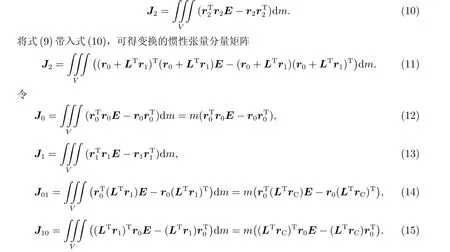
將式(12)～(15)帶入式(11)，得變換關系

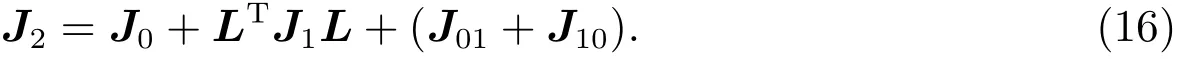
分幾種情況討論：

1) 當r0= 0 時，即局部坐標系原點O1與全局坐標系原點O2重合，此時為純旋轉變換，式(16)簡化為

2) 當r0?= 0 且L=E時，此時為純平移變換，變換關系為慣量平移定理，式(16)簡化為

3) 當rC=0 時，即局部坐標系原點O1與剛體質心重合，平移變換和旋轉變換的作用相互獨立，式(16)簡化為

4) 當r0?= 0 且rC?= 0 時，即局部坐標系原點O1與全局坐標系原點O2不重合，且局部坐標系原點O1與剛體質心不重合，則式(16)中存在交叉項，表明平移和旋轉變換存在耦合效應。

3 算例分析

考慮某飛行器艙段內三個組件的慣性矩、慣性積合成問題，已知組件在本體局部坐標系下的質量特性如表1 所示。

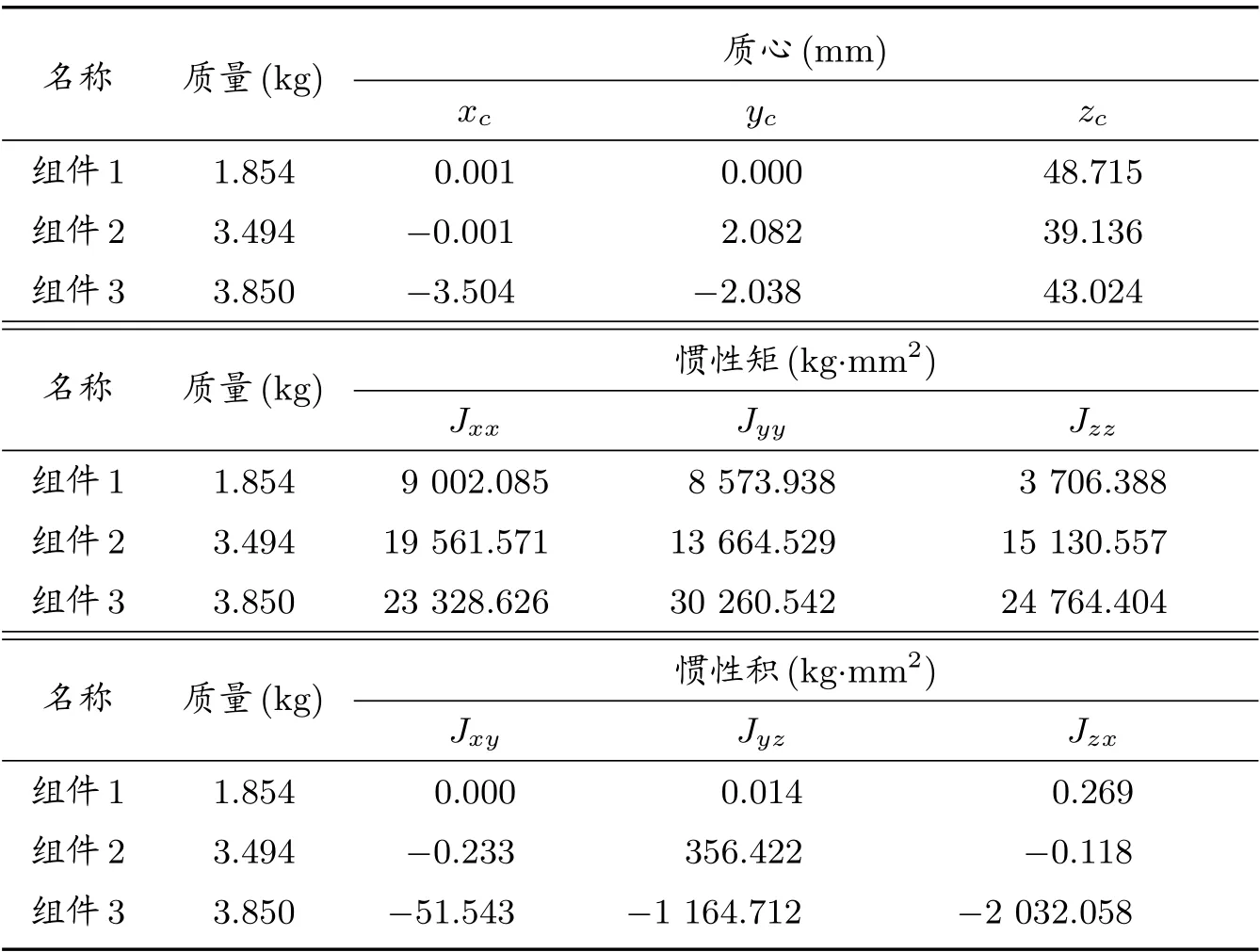
表1 組件本體局部坐標系下質量特性

假設三個組件未安裝時的本體局部坐標系與艙段全局坐標系重合，安裝好后本體局部坐標系相對全局坐標系先進行旋轉變換，然后進行平移變換，變換參數如表2 所示。

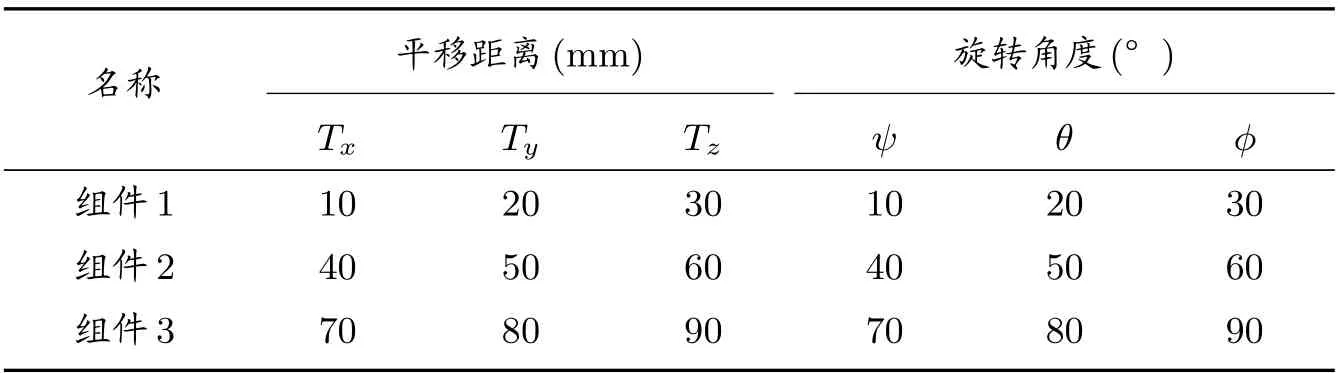
表2 組件平移和旋轉變換參數

組件安裝好后，相對于艙段全局坐標系的慣性矩和慣性積如表3 所示，其中計算值為本文計算結果，CAD 為三維軟件(NX UG 12.0)的測量結果。可以看出，計算結果與CAD 測量結果幾乎一致，微小的差異主要為數值舍入誤差導致，可忽略不計。結果表明，本文所推導的慣性張量復合變換的公式正確，可以作為工程中慣性矩和慣性積快速合成提供依據。

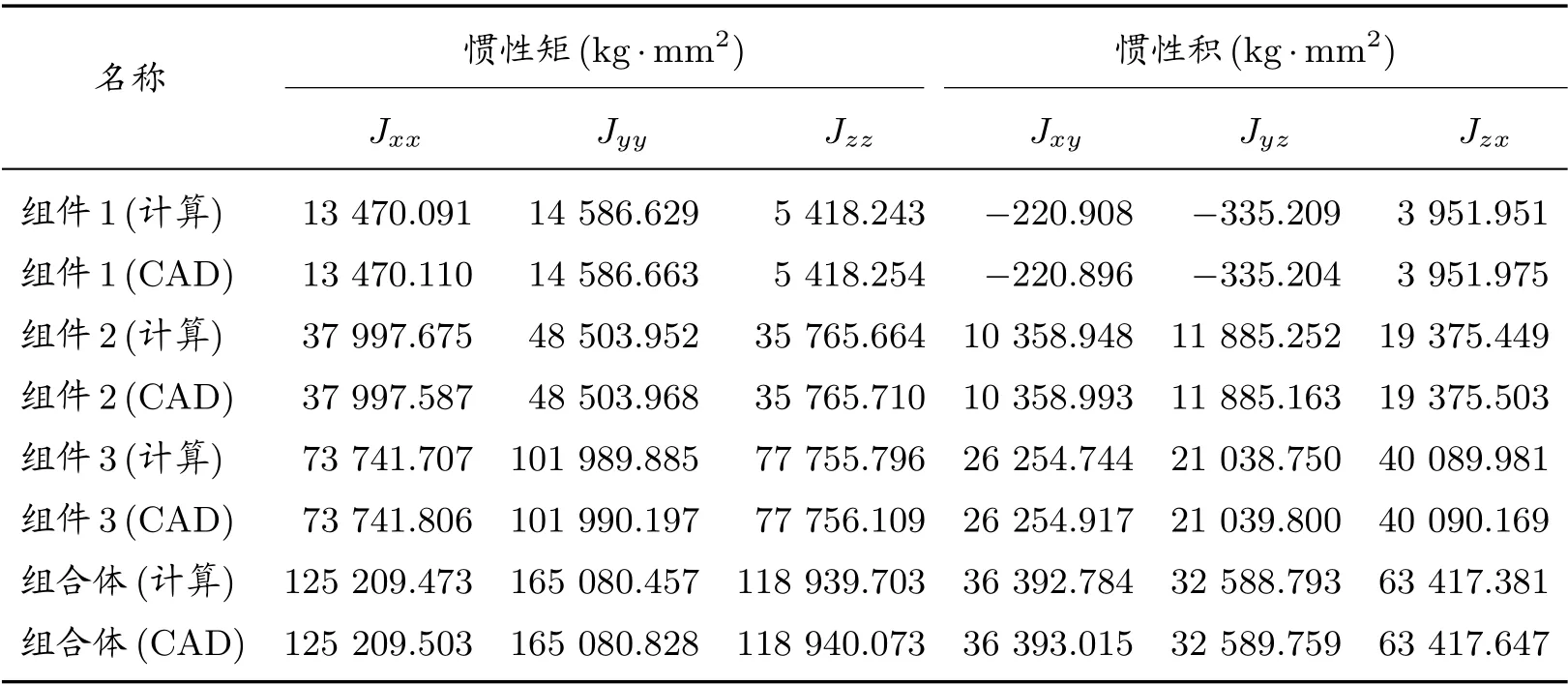
表3 組件全局坐標系下慣性矩、慣性積

4 總結

本文首先基于慣性張量的基本定義，采用矩陣變換推導出了慣性張量分量矩陣平移和旋轉復合變換的一般形式，然后給出了不同簡化條件下的結論。最后，通過某飛行器三組件慣性矩、慣性積合成的算例驗證了結論的正確性。

這種方法通過簡單的組合計算，就能夠在了解各組件隨時間變化的數據基礎上，適應組合系統的慣性張量計算需求。