基于IPSO-SVR模型的彎管部沖蝕率預測

于海躍， 劉浩楠

(長春工業大學 機電工程學院， 吉林 長春 130012)

0 引 言

在工業管道正常進行運輸中,不可避免地會在其中摻雜固體顆粒，從而發生固體顆粒的沖蝕，會對管道內壁尤其是管道彎頭處產生較大的沖蝕磨損，當腐蝕和沖蝕發生耦合時,其沖蝕率會進一步加大，而管道內壁因固體顆粒對管道內壁的沖蝕作用會導致內壁變薄，由此造成的應力聚集是事故發生的主要原因，而準確地預測管道的沖蝕率能夠為管道的剩余使用壽命預測以及維修策略的制定提供強有力的支持。董爭亮等[1]采用CFD數值模擬方法對90°彎管內壁的沖蝕問題進行研究，使用最小二乘法進行非線性擬合，并且得到了多種因素對彎管沖蝕的影響規律。胡瑾秋等[2]以正交實驗為基礎,得出各因素對沖蝕磨損結果的影響排序，得到了彎頭形態與流速是工程設計時首先考慮的因素。孫曉陽等[3]引入蒙特卡羅方法(DSMC)結合CFD數值模擬對管道進行沖蝕預測，通過5種不同的沖蝕模型對比發現，在保證預測精度的前提下,可節省大量算力。黎偉等[4]通過CFD-DPM模型求解彎管在流體作用下固體顆粒的沖蝕問題，并得到沖蝕位置主要在彎管出口的水平兩側,以及彎管入口的垂直兩側。Zahedi P等[5]使用相關的實驗參數作為預測變量，利用機器學習算法中的隨機森林算法來預測侵蝕率，并在不同條件下用測試數據驗證預測結果。Zhu H J等[6]研究受侵蝕彎管中的溫度分布，并找到一種新的方法來預測侵蝕削減管壁的厚度。Yu W C等[7]對90°標準彎頭中的壁面侵蝕進行了CFD研究，采用基于Euler-Euler方法的顆粒湍流動能模型進行侵蝕預測，其結果與實驗結果較為吻合。

綜上所述，目前使用數值模擬的方法針對彎管沖蝕率的研究較多，對特定情況下的預測準確率高，且可解釋性強，但是對先驗知識的要求也較高，文中將以數據角度為基礎，以機器學習與智能優化算法為手段，為管道彎頭部沖蝕磨損的預測提供新思路。

1 SVR算法

SVR是由統計學習理論為基礎衍生出來的監督學習算法，該算法的適應性強，在二維平面或者多維空間中仍有不錯的表現，能夠較有效地避免過擬合的出現，同時也能在小樣本數據中取得較好的效果，SVR與支持向量分類在使用過程中原理大致相同。SVR 的主要優點之一是無論輸入特征維度的大小，其計算的繁雜程度不會被影響;另一方面，在具有較高泛化能力的同時，也能進行精確預測。

SVR通過計算求解得到最優超平面，建立以

f(x)=wTx+b

為中心，2ε為寬度的間隔帶,使得各個數據點與超平面的距離都小于ε,

f(x)=wTφ(x)+b,

(1)

式中：φ(x)----非線性函數，其作用是將x映射到高維空間，與f(x)構成線性關系;

w，b----分別為權重和偏置;

f(xi)----輸出的預測值。

SVR的優化問題為

(2)

s.t.yi-wTxi-b≤ε,

wTxi+b-yi≤ε,

式中：yi----實際值。

(3)

s.t.yi-wTxi-b≤ε+ξi,

式中:C----損失權重的常數。

進一步將拉格朗日乘子與核函數[8]引入 SVR,

(4)

式中：m----樣本數量;

k(xi，x)----核函數。

(5)

式中:σ----核函數的寬度。

SVR模型精度主要取決于其中的損失權重常數C和高斯核函數中的參數γ。損失權重常數C過小時，對間隔帶以外的樣本數據懲罰較小，訓練誤差較大，在預測沖蝕磨損時的誤差也較大，如果損失權重常數C過大時，對間隔帶以外的樣本數據懲罰較大，模型精度隨之提升，但其泛化性會降低，往往導致模型過擬合的出現；核函數的參數γ則是影響了支持向量之間的聚合程度，γ越小，支持向量之間關系越不緊密，因此,在擬合過程中模型會變得特別復雜，泛化能力就會降低；γ越大，則支持向量之間就會越緊密，沖蝕預測模型難以達到預期的精度，因此，引入IPSO智能優化算法的根本目的則是找到最合適的C與γ。

2 IPSO優化算法

粒子群優化算法(PSO)是Kennedy J等[9]和Eberhart R等[10]提出的基于群體智能的全局隨機搜索的智能優化算法，該算法在工程領域以及其他領域中被廣泛使用，以解決各種優化問題。算法初始化會生成隨機粒子，通過不斷迭代尋找全局最優解，每次迭代過程會產生當代種群中的個體極值pbesti，個體極值與全局極值gbest進行對比，通過兩個極值相比，從而進行不斷更新。其原理如下。

假設在一個D維的目標搜索空間中，有N個粒子組成一個群落，其中第i個粒子表示一個D維的向量，

Xi=(xi1，xi2，xi3，…，xiD)，i=1，2，…，N。

粒子i的第d維速度更新為

(6)

粒子i的第d維位置更新為

(7)

式中：c1----個體學習因子，c1越大，粒子越傾向于以往個體所達到的極值;

c2----社會學習因子，c2越大，粒子越傾向于全局極值;

vi----粒子i的速度向量;

r1,r2----[0，1]上的隨機數;

w----慣性權重系數,w越大，其搜索范圍越大。

傳統PSO算法在尋優過程中會存在容易陷入局部最優和收斂速度較慢等問題，其算法的效率較難保證，因此，文中引入粒子自適應權重系數，使得粒子慣性權重能隨著算法迭代代數增加而發生改變，從而使得算法在迭代初期能夠獲得更大的搜索范圍，避免陷入局部最優，而在算法迭代后期能夠縮小搜索范圍，不易錯過全局最優解。自適應慣性權重系數為

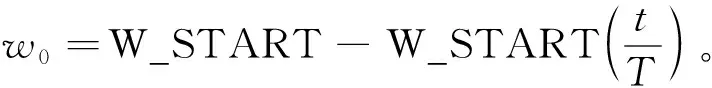
(8)

改進粒子群算法步驟如下：

1)初始化粒子群，并設定最大迭代次數T，當前迭代次數為t。

2)計算各個粒子的適應度值。

3)計算每個粒子的適應度值與其迭代的最佳位置pbesti的適應度值相比，若較好，則更新為當前的個體最佳位置。

4)計算每個粒子的適應度值與全局最佳位置gbest的適應度值相比，若較好，則更新為全局最優位置。

5)引入自適應權重w0，根據速度、位置公式對粒子的速度和位置進行優化，從而更新粒子位置。

6)如未達到最大循環數T，則返回2)繼續進行計算。

3 IPSO-SVR模型構建

在數學最優化問題中，Rosenbrock 函數是一個用來測試最優化算法性能的非凸函數，由Howard Harry Rosenbrock在1960年提出Rosenbrock函數的定義為

f(x，y)=(1-x)2+100(y-x2)2。

(9)

Rosenbrock函數的每個等高線大致呈拋物線形，其全局最小值也位于拋物線形的凹形區域中。由于凹形區域中的值變化較小，要找到全局最小值較為困難。其全局最小值位于 (x,y)=(1，1)點，數值為f(x,y)=0。第二項的系數不同，但不會影響全局最小值。其函數圖象如圖1所示。

圖1 Rosenbrock函數圖象

使用傳統PSO算法與IPSO算法進行對比，實驗結果見表1。

表1 PSO、IPSO算法對Rosenbrock函數求解全局最小值結果比對

傳統PSO算法雖然能夠尋得局部極小值，但是對于全局最小值的搜索依然較為困難，而IPSO算法能夠保證每一次都能尋找到全局最小值。

PSO和IPSO適應度迭代過程適應度進化曲線分別如圖2和圖3所示。

圖2 PSO適應度迭代過程適應度進化曲線

圖3 IPSO適應度迭代過程適應度進化曲線

圖3相較于圖2，傳統PSO算法在30代左右開始收斂，IPSO算法在10代左右已經開始收斂，這是由于自適應慣性權重的引入使得算法能夠避免陷入局部最優，提升了尋優能力以及收斂速度。

實驗具體參數設置為：群體粒子個數N=100；粒子維數D=2；最大迭代次數T=200；學習因子c1=1.5，c2=1.5；PSO慣性權重W=0.7；IPSO初始慣性權重W_START=0.9，分別使用PSO與IPSO進行全局最小值的搜索。

由以上結果可以得出，IPSO在尋優能力以及算法的收斂速度方面都優于原本的PSO。

IPSO-SVR模型步驟如圖4所示。

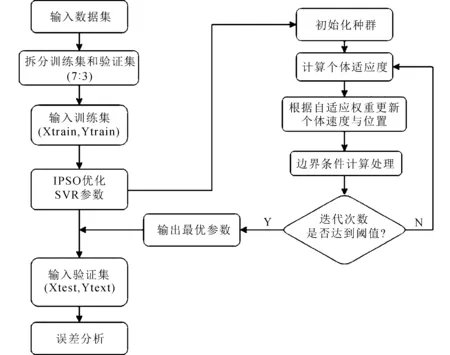
圖4 IPSO-SVR模型流程

4 IPSO-SVR模型預測彎管部沖蝕率

文中選擇201個較為廣泛的實驗數據點組成的數據集[5]，數據集1(源自Vieira (2014)，Parsi (2015)，Pyboyina (2006)，Muzamder (2004)，Salama (1998)-AEA Data)中包含6個特征，分別為管道材料、管道直徑、粒子尺寸、流體黏度、流體表面速度、氣體表面速度。

數據集2(源自Bourgoyne (1989)，Kesana (2013)，Vieira (2014)，Salama (1998)-AEA Data)中包含4個特征，分別是管道材料、管道直徑、粒子尺寸、氣體表層速度。數據集的數據分布見表2。

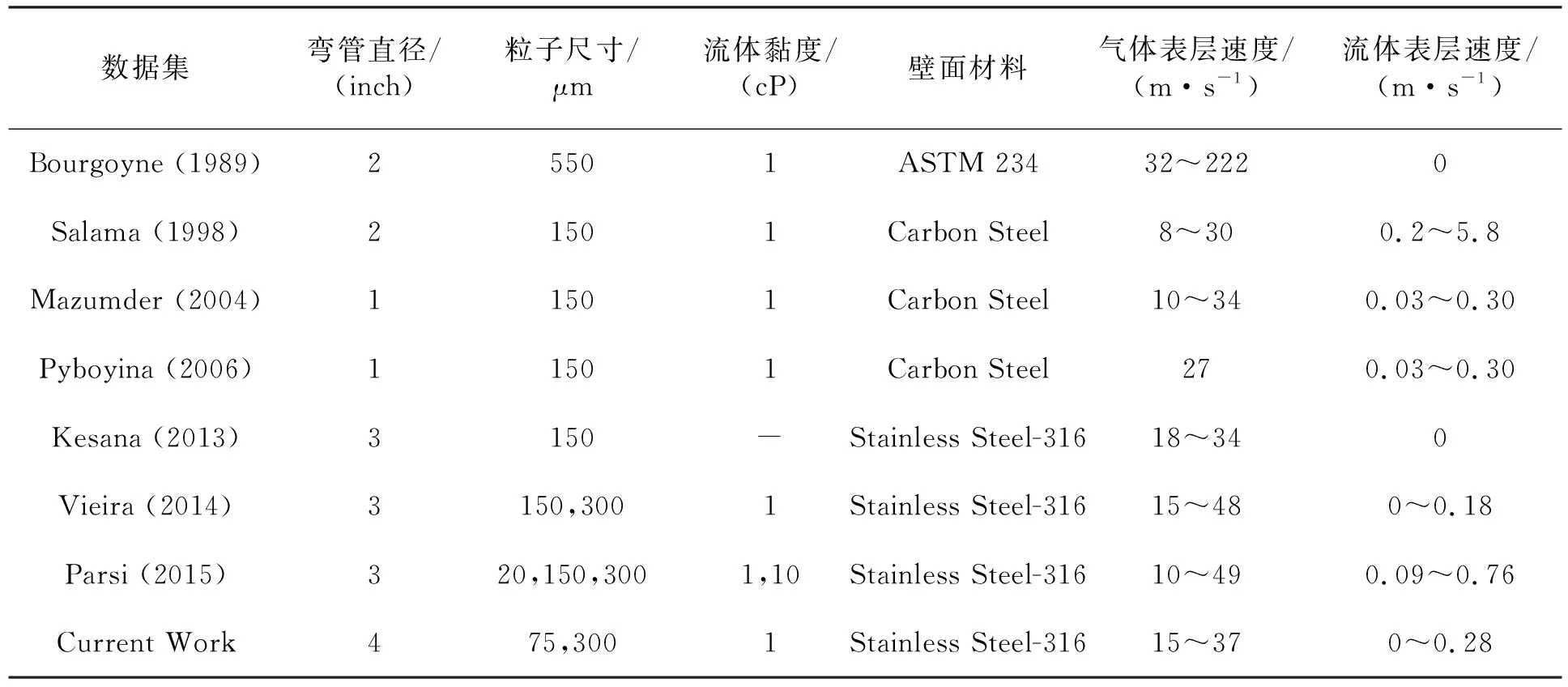
表2 沖蝕數據參數分布

文中將用三個指標對SVR模型與IPSO-SVR模型進行比較，分別為決定系數(R2)、平均絕對誤差(Mean Absolute Error， MAE)、均方誤差(Mean Square Error， MSE)，其定義分別為：

(10)

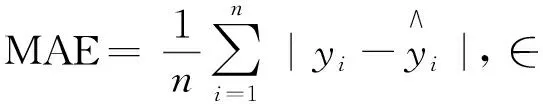
(11)

(12)

式中：n----預測樣本的數量;

yi----實際實驗中的沖蝕磨損值;

采用SVR與IPSO-SVR兩種算法對彎管沖蝕率預測結果分別如圖5～圖8所示。

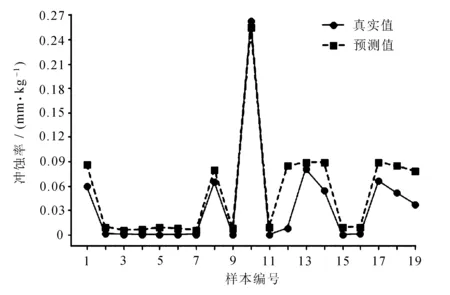
圖5 SVR預測數據集1結果圖

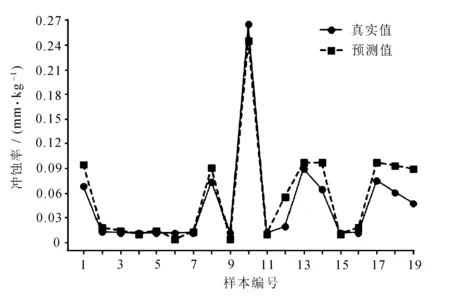
圖6 IPSO-SVR預測數據集1結果圖

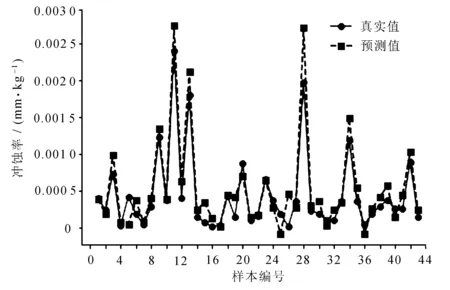
圖7 SVR預測數據集2結果圖

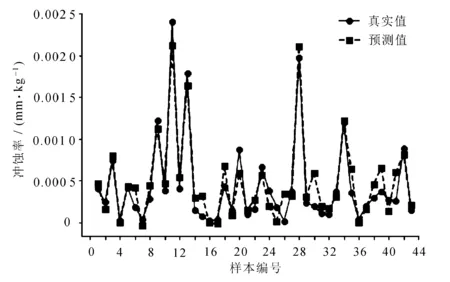
圖8 IPSO-SVR預測數據集2結果圖

使用IPSO-SVR模型分別對數據集1與數據集2的R2最高可達0.900 5與0.888 2，相較于SVR模型分別提升約6%與5.5%；MAE分別降低0.038 1與0.017 2；MSE分別降低0.031 7與0.009 4。經過IPSO優化后的SVR模型可以更為擬合地預測彎管部的沖蝕率，其誤差在減小，R2在提高。

數據集1和數據集2算法的評價指標對比分別見表3和表4。

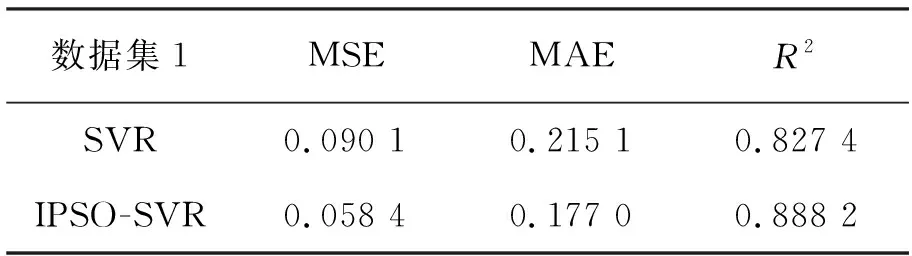
表3 數據集1中算法的評價指標對比

表4 數據集2中算法的評價指標對比

5 結 語

首先對粒子群算法進行了改進，并使用Rosenbrock函數對粒子群算法以及改進粒子群算法的性能進行比對，之后使用改進粒子群算法對支持向量回歸模型進行優化，最后使用兩個數據集對模型進行訓練，并對管道彎頭處的沖蝕率進行預測。通過結果可得到以下結論：

1)與傳統粒子群算法相比，改進后的粒子群算法具有更好的全局搜索能力，能提高大約2倍的收斂速度。

2)使用改進后的粒子群算法對支持向量回歸算法進行優化后得到IPSO-SVR模型，相較于一般的支持向量回歸，IPSO-SVR算法的預測精度最高可達90.05%，且誤差也更小，能夠更為準確地預測管道彎頭部位的沖蝕率。