β擾動(dòng)的隨機(jī)SI系統(tǒng)的漸近行為

劉振文

(吉林建筑科技學(xué)院 基礎(chǔ)科學(xué)部， 吉林 長(zhǎng)春 130114)

0 引 言

數(shù)學(xué)建模已經(jīng)成為分析傳染病流行和控制的重要工具，大多數(shù)傳染病模型都來(lái)源于經(jīng)典的Kermack W O等[1]SIR模型，與已感染者個(gè)體接觸后易感染者成為已感染者。最近，生態(tài)流行病學(xué)模型已引起人們注意力。相關(guān)文獻(xiàn)非常多，為方便起見(jiàn)，我們只提一篇述評(píng)[2]和幾本書(shū)[3-4]，假設(shè)所研究種群與其他種群沒(méi)有聯(lián)系，也就是說(shuō)，這些傳染病模型只用來(lái)描述一種傳染病的傳播，很多學(xué)者得到了閾值理論。

在自然界里種群并不單獨(dú)存在，當(dāng)其他種群傳播疾病時(shí)，這個(gè)種群也與其他種群爭(zhēng)奪生存空間和食物，或者被其他種群捕食。因此，當(dāng)我們研究生態(tài)流行病學(xué)的動(dòng)力學(xué)行為時(shí)，考慮種群間的相互作用具有重大的生物意義。目前為止，把這兩個(gè)領(lǐng)域聯(lián)系起來(lái)的研究還很少。文中首先介紹捕食者基于最經(jīng)典的生態(tài)流行病學(xué)模型，即SI模型，以研究捕食者的行為對(duì)傳染病的影響。為此，只研究最簡(jiǎn)單的情形，即捕食者只吃有病的食餌，這與實(shí)際情況是相符的，有病的食餌相對(duì)來(lái)說(shuō)缺少活力，更容易被捕食者捕獲。或者說(shuō)有病食餌的行為被迫發(fā)生改變，以至于活動(dòng)在更容易被捕獲者捕獲的區(qū)域。例如，魚(yú)和水生蛇停留在更靠近水面的位置，蛇停留在植物的頂端而不是被植物覆蓋。Xiao Y等[5]提出，當(dāng)老鼠遭受細(xì)粒棘球絳蟲(chóng)疾病時(shí)，狼捕獲老鼠成功率更大。

這樣就得到兩個(gè)種群：N表示食餌種群的總密度；Y表示捕食者種群的總密度。

我們做如下假設(shè):

1)在無(wú)病條件下，食餌種群的增長(zhǎng)符合Logistic規(guī)律，環(huán)境容納量為K>0，內(nèi)稟增長(zhǎng)率為常數(shù)r>0，則有

2)在有病條件下，食餌種群總數(shù)N由兩部分組成：一類是易感染者(記作S)，一類是已感染者(記作I)，則有

N(t)=S(t)+I(t)。

3)為方便起見(jiàn)，我們僅假設(shè)易感染者S具備繁殖能力，且服從上述Logistic規(guī)律。也就是說(shuō)，已感染食餌I被死亡除去了，即已感染食餌或者已死亡率正常數(shù)c>0，死亡或者在繁殖前被捕食者捕獲。然而，已感染種群I與S一起對(duì)種群的增長(zhǎng)有貢獻(xiàn)，并使之達(dá)到環(huán)境容納量。

4)傳染病只在食餌中傳播并且不遺傳。已感染者不會(huì)康復(fù)或者獲得免疫力。考慮最簡(jiǎn)單的大范圍行為發(fā)散率βSI，其中β>0表示轉(zhuǎn)移系數(shù)。這樣就建立了確定性SI模型：

(1)

系統(tǒng)(1)有如下平衡點(diǎn)：

E0=(0，0)，

E1=(K，0),R0<1，

在隨機(jī)波動(dòng)和隨機(jī)擾動(dòng)情況下，系統(tǒng)(1)受到環(huán)境白噪聲的影響，性質(zhì)有何改變?而就作者所知，目前對(duì)隨機(jī)SI系統(tǒng)的研究很少。文中首先對(duì)確定性系統(tǒng)(1)進(jìn)行線性擾動(dòng)，得到如下系統(tǒng)[7]：

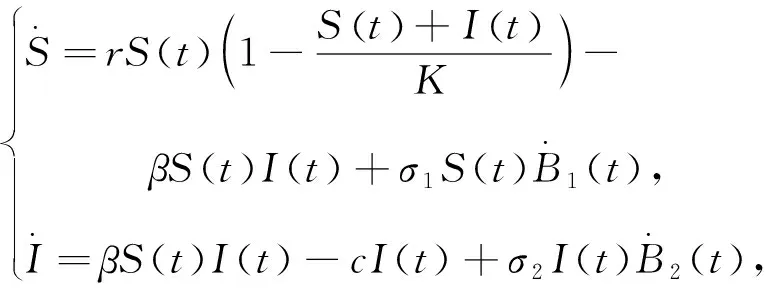
(2)

式中：Bi(t)----相互獨(dú)立的布朗運(yùn)動(dòng)，i=1，2;

σi----正的常數(shù);

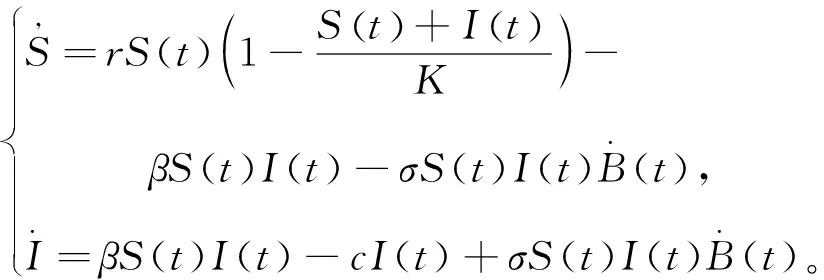
(3)

接下來(lái)用隨機(jī)分析理論研究系統(tǒng)(3)的隨機(jī)漸近性行為，以期待得到一些不同于相應(yīng)的確定性系統(tǒng)的結(jié)果。

文中令(Ω，F(xiàn)，{Ft}t≥0，P)表示帶有{Ft}t≥0且滿足通常條件(即單調(diào)增加且右連續(xù)的且F0包含所有的P零空集)的全概率空間。

1 系統(tǒng)(3)的正解存在唯一性

證明 對(duì)t≥0,考慮系統(tǒng)

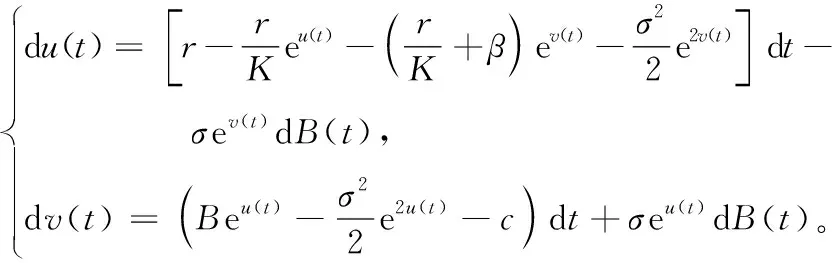
(4)

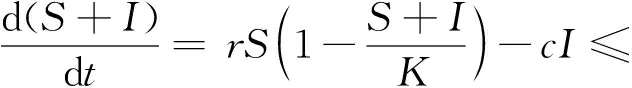
(5)

則

S(t)+I(t)≤

K。

(6)

現(xiàn)在,我們將證明這個(gè)解是幾乎必然全局的,就等價(jià)于證明τe=∞幾乎必然成立。選擇足夠大的k0≥0,使得S(0),I(0)全部位于區(qū)間[1/k0,k0]內(nèi)。對(duì)每一個(gè)整數(shù)k≥k0,定義

τk=inf{t∈[0,τe):min{S(t),I(t)}≤

1/kor max{S(t),I(t)}≥k}。

(7)

P{τk≤T}≥εfor allk≥k1,

(8)

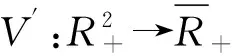
(9)

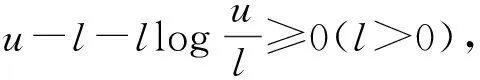
k′(I-b′)[(βS-c)dt+σSdB(t)]+

LV′dt+σ[-(S-a′)I+k′(I-b′)S]dB(t),

(10)

其中

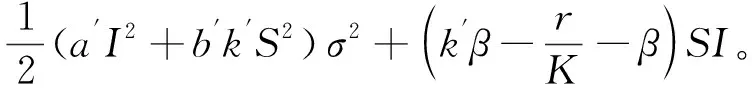
(11)

首先,選取

滿足

其次,選取

和

滿足

和

則

(12)

因此

(13)

則推得,

E[V′(S(τk∧T),I(τk∧T))]≤V′(S(0),I(0))+

(14)

當(dāng)k≥k1時(shí),令Ωk={τk≤T}且由式(8)有,P(Ωk)≥ε。注意到對(duì)每一個(gè)ω∈Ωk,在S(τk,ω),I(τk,ω)中至少有一個(gè)達(dá)到k或1/k,因此

h′(k),

(15)

其中h′(k)是k的函數(shù),且

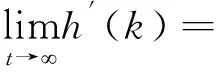
再由式(8)和式(14)有

E[1Ωk(ω)V′(S(Tk∧T),I(Tk∧T))]≥

εh′(k),

(16)

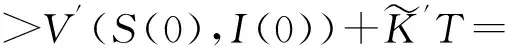
注1從定理可以得到

I(t)>0,S(t)+I(t)≤K},

(17)

是系統(tǒng)(3)的正不變集。從現(xiàn)在開(kāi)始，我們總是假設(shè)初始值(S(0),I(0))∈Γ。

2 系統(tǒng)(3)的滅絕性和持久性

定理2今(S(t),I(t))為系統(tǒng)(3)滿足初始條件(S(0),I(0))∈Γ的解。假設(shè):

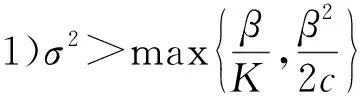
證明 由Itǒ's公式,有

(18)

令

(19)

下面分兩種情形討論。

(20)

則有

(21)

和

(22)

令

它是一個(gè)實(shí)值連續(xù)局部鞅,M(0)=0且有

K2<∞a.s.

(23)

再由強(qiáng)大數(shù)定律,證得

(24)

幾乎必然成立。再由式(22)得到

(25)

幾乎必然成立。由條件1)非常容易得到

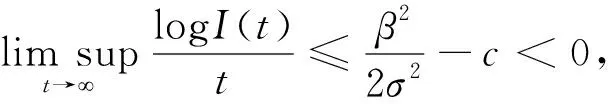
(26)

幾乎必然成立。也就是說(shuō),I(t)幾乎必然以指數(shù)收斂于0。換句話說(shuō),已感染者依概率1死亡。

(27)

則

(28)

類似于(i)中的討論,得到

(29)

幾乎必然成立,使用條件2),可得到

(30)

幾乎必然成立。即I(t)以指數(shù)幾乎必然趨于0。換句話說(shuō),已感染者依概率1死亡。

再由Itǒ's公式,有

σIdB(t),

(31)

則有

(32)

和

(33)

再由上式,可得

(34)

幾乎必然成立。由于

(35)

幾乎必然成立。

我們得到

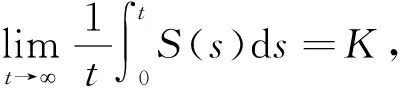
(36)

幾乎必然成立。