基于特征點對優化篩選的點云初始配準算法
郭 敏, 孫 夢, 呂源治, 李貞蘭
(1.長春工業大學 計算機科學與工程學院, 吉林 長春 130102;2.中國科學院長春光學精密機械與物理研究所, 吉林 長春 130033;3.吉林大學, 吉林 長春 130012)
0 引 言
隨著物聯網技術和三維立體視覺的不斷發展,三維點云數據處理技術在人工智能、虛擬重建、機器視覺等領域得到廣泛應用[1-3]。點云配準技術是點云處理技術的關鍵部分,點云配準質量是影響三維重建效果的重要因素。
自動配準、手動配準和依賴儀器配準是點云配準方式的三種形式[4]。目前主要采用自動配準技術,最常用的方法是由 Besl P J等[5]提出的迭代最近點(Iterative Closest Point, ICP)算法,它是當前點云配準過程中應用最廣泛的算法。雖然該迭代算法精確度較高,但對兩組點云的相對初始位置要求較高且容易陷入局部最優解[6]。針對此問題,目前點云配準主要采用先進行初始配準再進行精配準的方式[7]。初始配準算法主要包括主成分分析法、基于特征的配準算法以及基于投票機制的配準方法。基于特征的配準是指利用物體自身的點、線、面等幾何特征或紋理特征解計算變換參數[8],它是目前應用最為廣泛的初始配準算法,主要分為特征檢測、特征描述和特征匹配三個步驟。特征描述步驟中應用最為廣泛的是Rusu R B等[9]在2009年提出的一種FPFH用于描述點云特征。在特征匹配階段,RANSAC算法是一種應用較為廣泛的特征匹配方法[10],但存在有限次隨機性帶來的不穩定性和計算量較大等弊端。當輸入的點云中相似特征點較多時,僅依靠特征描述的相似程度搜索對應點[11],會出現較多的錯誤匹配點對,導致后續的點云配準結果較差。
針對上述問題,提出一種基于特征點對優化的初始配準算法,該算法能夠在優化對應點集的同時,規范化閾值的選取,減少了對初始配準結果的影響,為點云的精配準提供精確度較高的初始對應點集,從而實現對三維點云數據配準的目標。同時文中又基于三維坐標轉換的基本理論,羅德里格矩陣在迭代求解點云配準參數中的應用。
1 配準原理
三維點云初始配準的關鍵在于獲取較高精度的初始位置和精確的對應點對。為此,文中采用基于點云特征實現初始配準的算法流程如圖1所示。
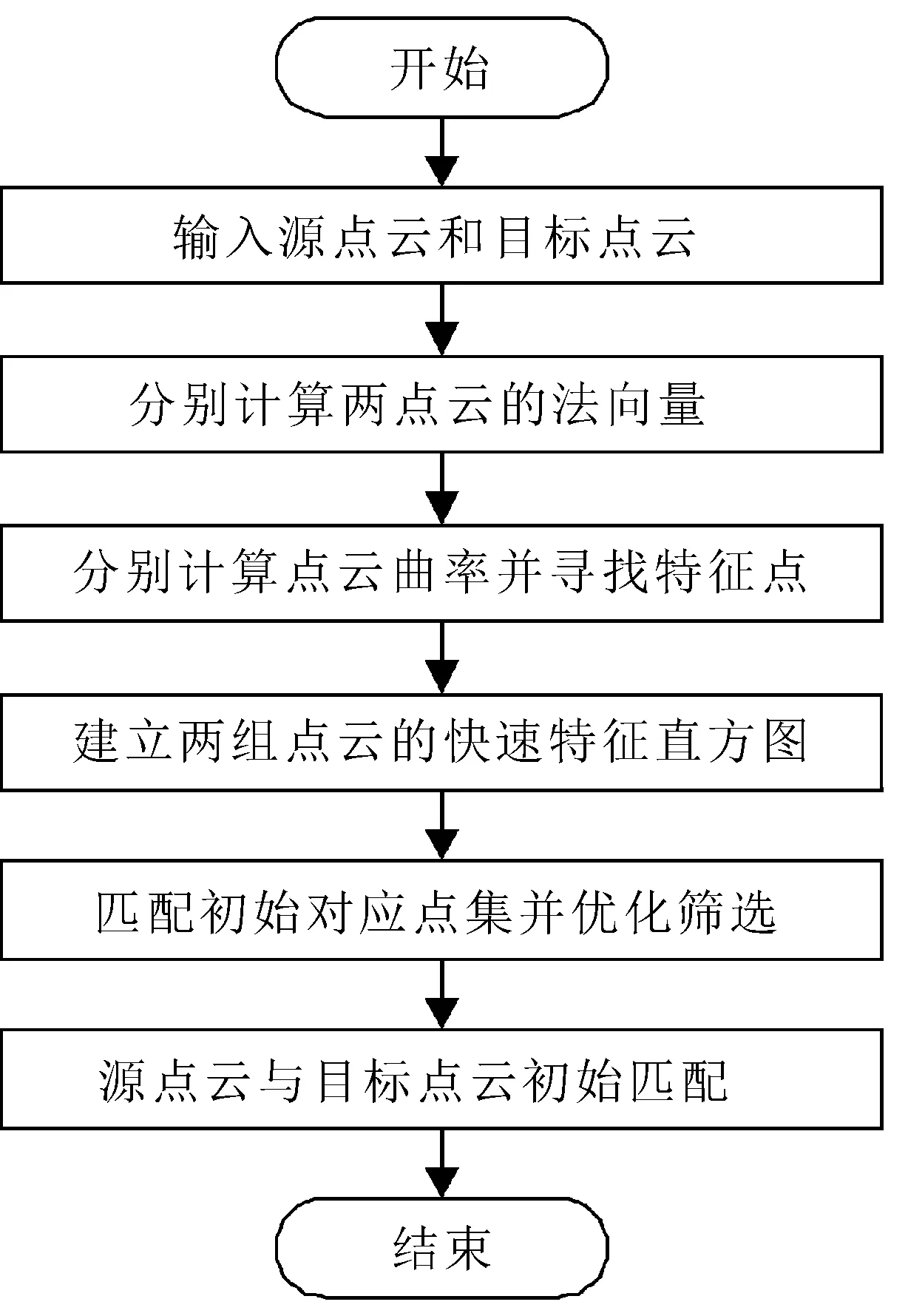
圖1 點云初始配準算法流程
首先,對輸入的兩組點云進行法線估計;其次,基于點云的曲率實現特征點的提取;再次,根據特征點建立點云的快速特征直方圖;然后,基于已經得到的直方圖實現初始對應點集的建立,并進行優化選取;最后,利用羅德里格斯旋轉公式求解初始變換位姿,以實現點云初始配準的目標。
1.1 計算點云法向量
采用主成分分析(Principal Component Analysis, PCA)[12]算法實現點云的法向量估計,首先,構建點云的KD樹并計算其鄰域內的中心點坐標;其次,構造點云的協方差矩陣,并計算該矩陣的特征值和特征向量;然后,將所求得的特征值按照從小到大的順序進行排序,最小特征值對應的特征向量就是點云的法向量;最后,對求得的法向量進行檢驗與調整,使得所有點云數據的法向量方向一致。
1.2 提取特征點
曲率能夠描述曲線或者曲面的彎曲程度,在三維點云中可以用來描述多個點所構成曲面的局部性質[13],常用的曲率有高斯曲率、平均曲率和主曲率。三維空間中某點的平均曲率表示曲面在該點的平均彎曲程度,文中基于平均曲率實現特征點的提取。
首先,將點云中第c個點Pc(c=1,2,…,N)(N表示點的個數)的曲率估計值為

(1)
式中:λ1,λ2,λ3----第c個點與其e個鄰域點所建立協方差矩陣的特征值,滿足λ1≤λ2且λ1≤λ3。
然后,設定曲率閾值
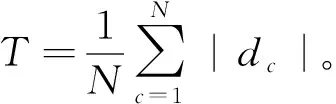
(2)
最后,根據曲率估計值dc與閾值T大小的比較,得到特征點集與非特征點集:曲率估計值大于閾值的點標記為特征點;否則,標記為非特征點,所有特征點組成特征點集,非特征點組成非特征點集。
1.3 建立快速點特征直方圖
快速點特征直方圖(FPFH)是一種能夠描述特征點鄰域內幾何特征的描述子,利用多個不同維度的直方圖來描述特征點的法向量特征,從而描述特征點鄰域內的幾何特征信息。在三維空間中,空間內任意一點與其K鄰域內的每一個點兩兩連接,將點與點之間的幾何特征定量化表示,基于點云的三維坐標信息與法向量之間的相互作用關系,描述出點云的幾何特征。查詢點Pq與其K鄰域點的FPFH計算關系如圖2所示。
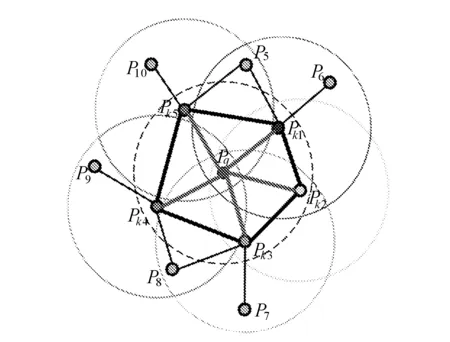
圖2 查詢點Pq與其鄰域點FPFH描述子計算原理圖
FPFH描述子僅在查詢點與鄰域點之間建立幾何關系,為了更好地描述任意兩點Ps與Pt對應法向量之間的關系,選擇其中一點作為坐標原點,在兩點間構造局部坐標系,如圖3所示。

圖3 兩點間局部坐標系
首先分別查詢兩點的法向量,其次以法向量為其中一個坐標軸,然后根據法向量求剩下兩個坐標軸的單位向量,再根據向量求其夾角。三個單位向量u,v,w計算如下:
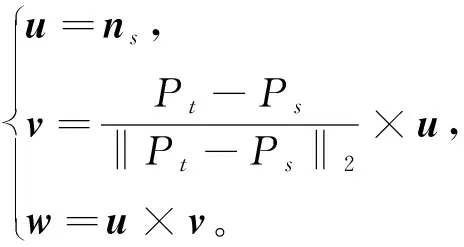
(3)
根據三個單位向量u,v,w可計算法向量與局部坐標系各坐標軸之間的夾角。
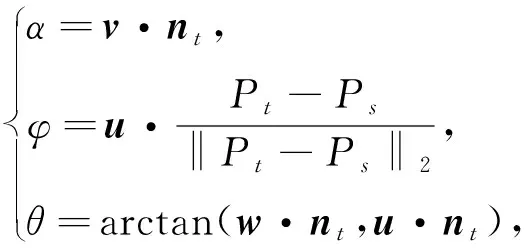
(4)
α,φ,θ這三元組也被稱為簡化點特征直方圖,記作SPFH。對于某個查詢點Pq來說,其FPFH的建立過程如下:
1)求該點的簡化點特征直方圖SPFH(Pq)。
2)利用已經得到的SPFH(Pq)并根據下列公式計算FPFH特征
FPFH(Pq)=SPFH(Pq)+
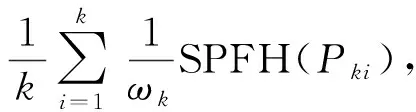
(5)
式中:ωk----權重;
k----鄰域點的個數。
1.4 優化篩選特征點對
基于點云的特征直方圖尋找源點云與目標點云間的對應點對,采用最鄰近搜索方式查找源點云與目標點云中特征直方圖相似的點作為初始對應點集,設H(P)表示源點云的特征直方圖,H(Q)表示目標點云的特征直方圖。對于源點云中的一點p在H(Q) 中能找到與H(p) 極為相似的最鄰近點, 同理,對于目標點云中的一點q在H(P) 中能找到與H(q)極為相似的最鄰近點,組成初始的對應點集A1。
由于此時對應點集的誤差較大,所以要對其進行兩次優化篩選。
1.4.1 一一對應原則
在獲取初始的對應點集時,是基于點特征直方圖的相似程度來確立的,存在源點云中的一點(目標點云中的一點)對應目標點云中多個點(源點云中多個點)的情況。此時需要優化點云以實現點云一對一的目標,即對于初始對應點集中的一組點對(p,q)需滿足p的最鄰近點是q,q的最鄰近點是p, 優化后得到新的點集為A2。
1.4.2 近似等距離原則
等距離原則是源點云中的一點p1到目標點云的對應點q1的距離等于源點云中另一點p2到其目標點云中對應點q2的距離,同時源點云中p1與p2的距離等于目標點云中q1與q2的距離,兩點集中點間距離模仿圖如圖4所示。
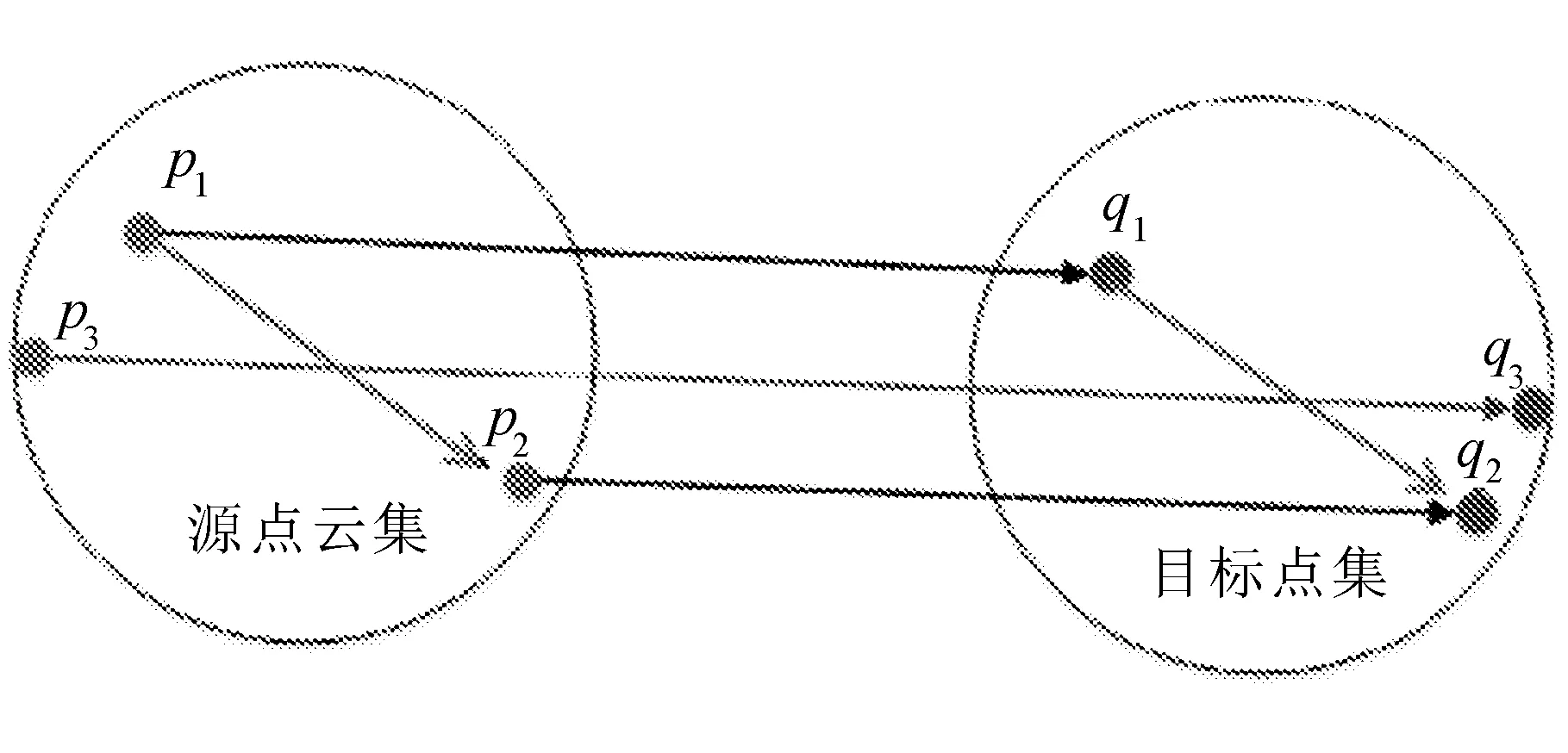
圖4 兩點集中點間距離模仿圖
(p1,q1)、(p2,q2)為模擬點云中正確的對應點對,(p3,q3)是一組錯誤點對。
由于實際中存在誤差,不能達到距離值完全相等的目標,所以設定一個容忍小范圍誤差的閾值ε1和ε2,以剔除點集A2中錯誤的對應點對。
其中,ε1的計算過程如下。首先,設L={l1,l2,l3,…,lF-1},表示兩組對應點中源點云兩點歐式距離與目標點云中兩點歐式距離比值的集合,其中F表示A2對應點對的個數,L中集合參數可由下式計算
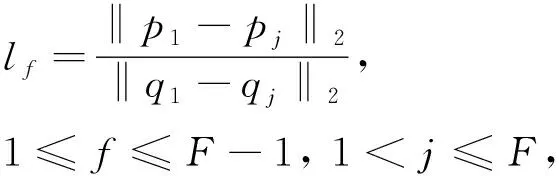
(6)
然后,根據式(6)可得ε1的表達式為
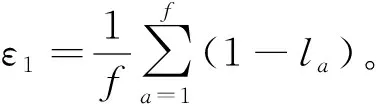
(7)
同理也可得到ε2,設M={m1,m2,m3,…,mF-1}表示兩組對應點中源點云兩點歐式距離與目標點云中兩點歐式距離比值的集合。M中集合參數可根據下式計算
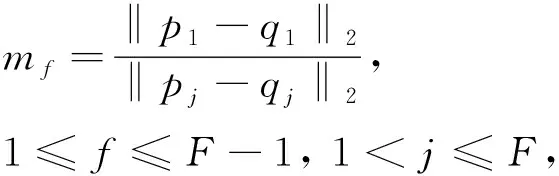
(8)
然后,根據式(8)計算
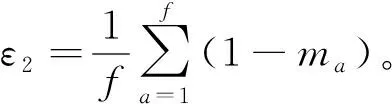
(9)
對于A2中的任意兩組對應點對需滿足
|lf-1| ≤ε1且 |mf-1| ≤ε2,
(10)
經過上述兩次優化篩選得到最終的對應點集。
2 點云初始配準
為計算點云配準的旋轉和平移矩陣,需要經過多次的迭代遍歷過程,輸出使配準誤差值最小情況下的旋轉矩陣和平移矩陣。具體步驟如下:
1)隨機選取n(n≥3) 組對應點;
2)通過羅德里格斯公式求旋轉矩陣和平移向量[14];
3)根據式(11)計算此時的配準誤差為
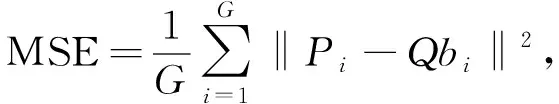
(11)
式中:Qb----目標點云旋轉后的點集;
G----對應點對的個數;
4)重復上述3個步驟,直到滿足迭代次數為止,輸出最小誤差對應的旋轉矩陣和平移向量。
通過羅德里格斯公式求旋轉矩陣和平移向量的過程。

(12)
式中:D=1-cosθ。
根據旋轉關系,將目標點云中一點(X,Y,Z)轉換到源點云坐標系下,得到點(X′,Y′,Z′),兩個坐標點之間的關系為
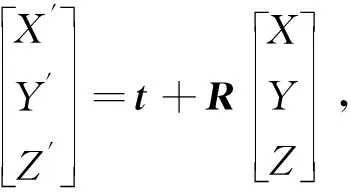
(13)
式中:t----平移向量;
R----旋轉矩陣。
通過反對稱矩陣可以構建羅德里格矩陣表達為
R=(I+S)(I-S)-1,
(14)
式中:S----旋轉向量對應的反對稱矩陣;
I----單位矩陣。
設旋轉向量為
a=[ax,ay,az]T。
根據已有的任意三個公共點,求解轉換參數,(Xi,Yi,Zi)和(Xj,Yj,Zj)兩組對應點對式 (11)相減得到:
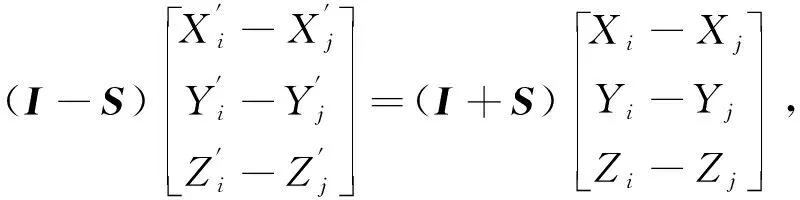
(15)
對式(15)代入R,并整理轉換可得到:
1)令
A和B中Δ表示求得的差值。
ΔXij=Xi-Xj,
隨機選取3組及以上點云時,計算得到的矩陣A和矩陣B分別垂直合并,則AS=B,根據最小二乘原理可求得a=(ATA)-1ATB,對其進行單位化得到旋轉軸O。
2)旋轉角的取值為
式中:max(a)----a中列向量的最大值。
3)將求得的參數代入羅德里格斯旋轉矩陣的展開式,可得到旋轉矩陣,根據旋轉前后兩坐標點的關系,可求得平移向量。
3 實驗結果及分析
3.1 實驗環境與數據來源
實驗采用計算機硬件環境為Intel(R) Core(TM) i5-5200U CPU @ 2.20 GHz 2.19 GHz,4 GB內存,軟件環境為Windows 10 操作系統,使用Matlab編程軟件。采用長春光機所自主研發的SVision751B型三維激光掃描儀對機器貓石膏像進行點云數據采集,原始點云數據及點云封裝圖分別如圖5和圖6所示。
圖5 原始點云

圖6 點云封裝圖
兩圖中左邊均為目標點云,右邊為源點云。
3.2 實驗結果與分析
為減少因數據冗余造成計算效率低下的問題,對圖5中的原始點云數據進行了精簡,以精簡后的點云作為輸入的點云數據集,按照圖1步驟完成點云配準實驗。源點云與目標點云法向量的求取結果,法向量的方向統一指向點云外側,源點云與目標點云的法向量如圖7所示。
圖7 源點云與目標點云的法向量
源點云與目標點云的特征點如圖8所示。
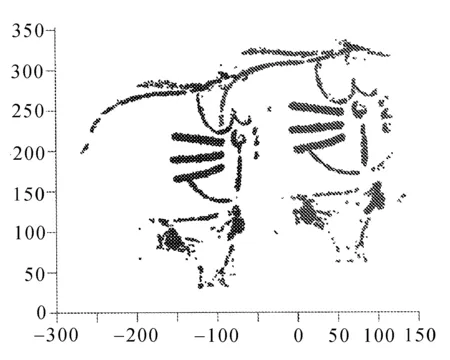
圖8 源點云與目標點云的特征點
特征點個數與輸入點云個數對比見表1。
源點云中提取到的特征點有8 424個,目標點云中提取到的特征點有8 082個。
利用特征直方圖,在目標點云與源點云中確立初始對應點集,共計8 424對,第1~1 000組對應點集如圖9所示。
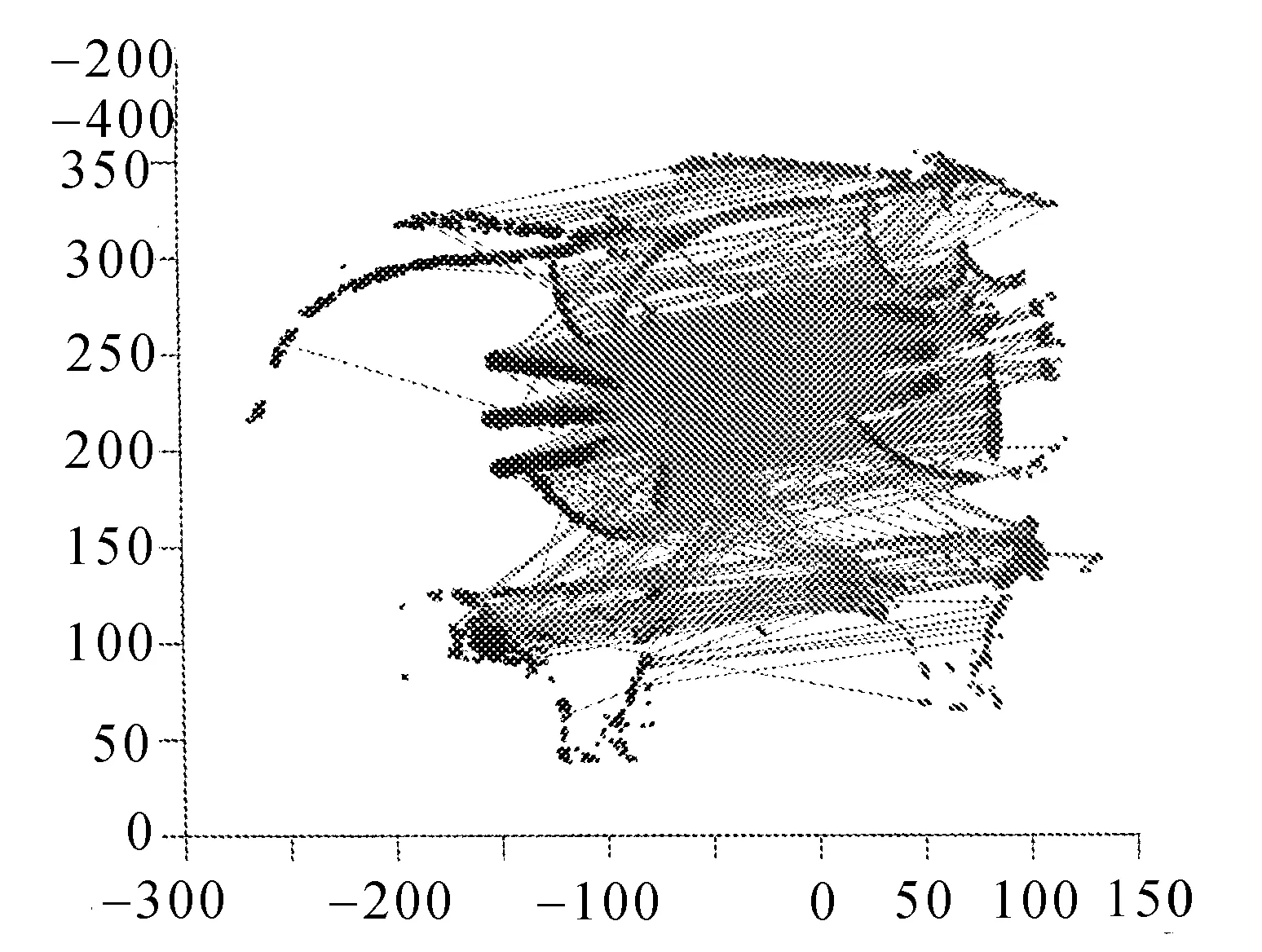
圖9 優化前的對應點集(第1~1 000組)
從圖中可以看出,此時的對應點集中存在較多的錯誤點對,運用文中提出的特征點對優化篩選算法進行處理后,得到新的對應點集,如圖10所示。
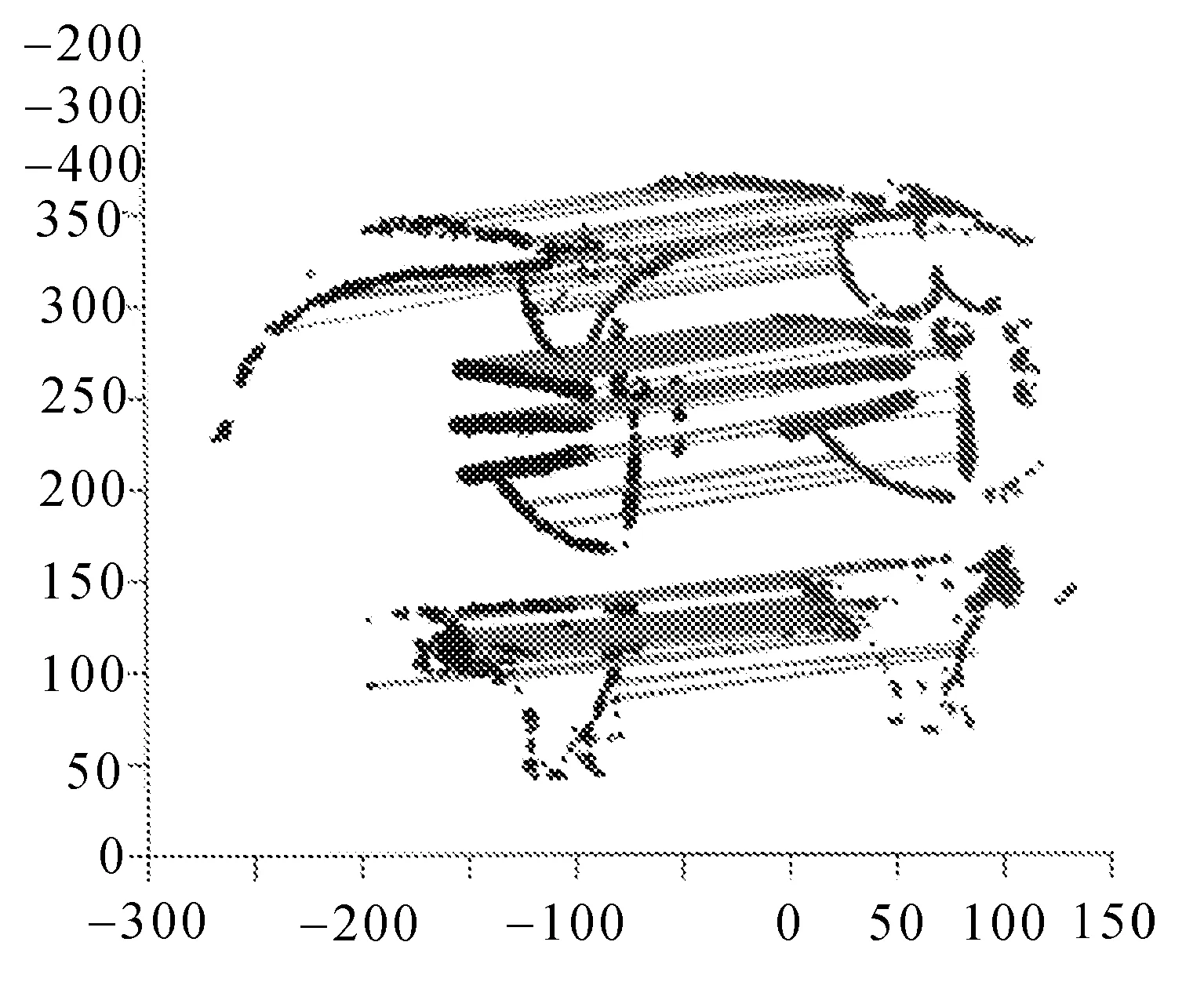
圖10 優化后的對應點集
相比圖9,新點集中對應點對質量較高。
記錄優化篩選前后點對個數的變化見表2。
通過數據對比發現,初始對應點集中錯誤點對的數量較多,若不對其優化篩選,將直接影響后續點云初始配準的精度,甚至導致配準失敗。

表2 對應點對的數量
為進一步驗證文中算法在精度及穩定性方面的性能,將所研究算法與基于RANSAC思想剔除錯誤點對的初始配準算法的實驗結果對比分析見表3。
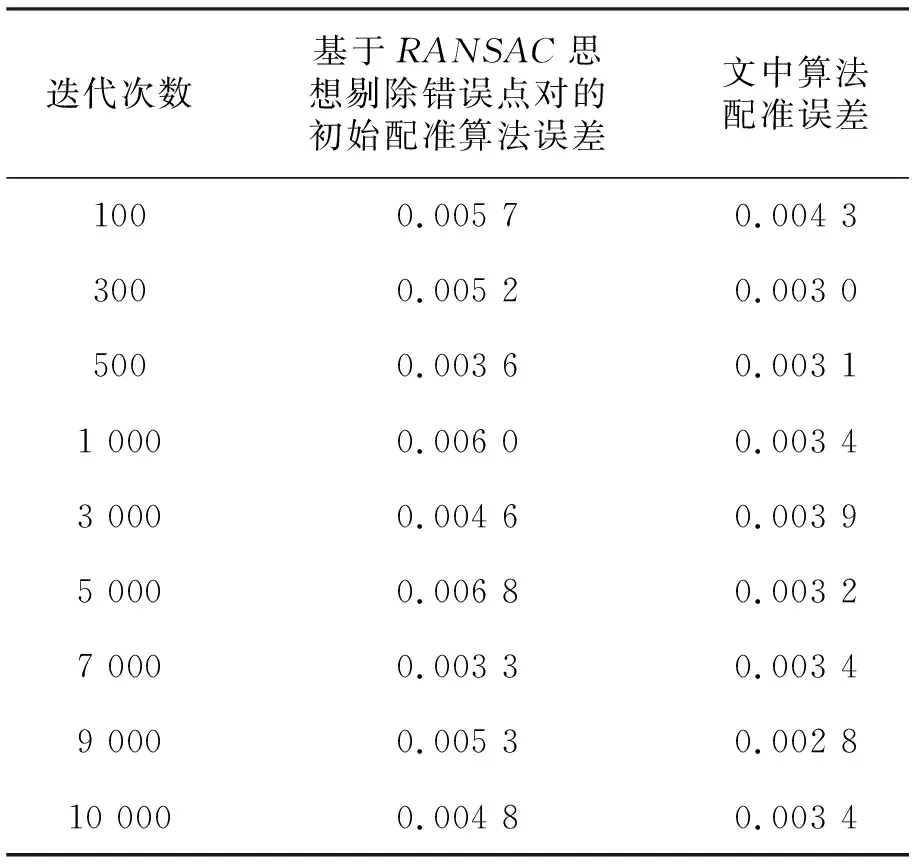
表3 不同迭代次數下配準誤差對比
實驗中不斷調整迭代次數,并分別記錄兩種算法在不同迭代次數下的配準誤差,對比發現,文中算法的配準誤差相對較低。迭代次數為1 000時,兩種算法的配準結果如圖11所示。
(a) 文中算法
結合表3中該迭代次數下的配準誤差對比分析(a)和(b)兩圖可發現,文中算法略優于基于RANSAC思想剔除錯誤點對的初始配準算法。
4 結 語
針對源點云和目標點云中特征點對容易產生錯誤匹配,從而導致初始配準精度較低的問題,文中對基于特征點對篩選優化的點云初始配準算法進行了研究,實驗結果表明,該算法的誤差較小,精確度較高,且穩定性較強。

