基于數值模擬對深埋引水隧洞地震響應研究

肖鑫華

(贛州市天鷹水利水電規劃設計有限公司，江西 贛州 341000)

1 概 述

隨著我國經濟的快速發展，水利工程建設中的引水隧洞工程項目也越來越多。眾所周知，我國幅員遼闊，山區眾多，屬于地震多發國家。如果在地震頻發區域建設深埋地下的引水隧洞工程，將面臨著巨大的困難。因此，針對引水隧洞的地震響應進行分析研究具有十分重要的意義。

為此，許多學者進行了深入研究。李帥[1]對近斷層地震帶脈沖特征提出新的方法，并進行驗證，分析了地震響應對脈沖參數的變化規律。禹海濤[2]對隧道的抗震情況進行了設計，推導出解析算法，由此分析并進行驗算。江志偉等[3]基于大型振動臺試驗進行數值模擬研究，對誤差值進行驗算，提高了其預測值的準確性。袁勇等[4]利用隧洞的制造特征和結構特性，建立動力學模型及進行公式推導，并將推導結果與數值模擬計算結果進行了對比。禹海濤等[5]介紹了隧洞的地震響應情況與試驗方法的進展，并由此進行了分析。余佳等[6]通過對引水隧洞的各種分析，選出引水隧洞施工方案的優選方案，并探究每個因素對施工方式的影響情況。袁平等[7]根據地層的參數特性，利用數值模擬對地層進行建模，探究地層隧洞施工方案的合理性。周澤林等[8]結合工程實況，基于數值模擬，對深埋巖體引水隧洞的受力情況開展了研究。

綜上可知，目前我國對于深埋地下引水隧洞的研究已取得較多研究成果，但以上研究成果均未考慮動靜荷載作用下引水隧洞的應力特征。本文通過數值模擬建模，并基于靜荷載條件和動荷載條件，對地震應力下引水隧洞的地震響應特征進行探究。

2 模型建立

2.1 工程概況

某城市某項目引水隧洞位于我國某地區，該地區多地震帶，且地勢險峻，地勢較高，經常發生地震情況。該引水隧洞在某水電站附近，其附近區域多為巖體區，巖體較為堅硬。在本工程應用中，其初始應力大于20 MPa，為硬度大的高應力巖體。在地震荷載作用下，建立非線性本構關系，并建立模型進行分析。

2.2 圍壓與破壞效應

本文通過三軸壓縮試驗進行圍壓不同情況下巖體三軸試驗，見圖1。同時，對試驗數據進行統計，將試驗的應力狀態和應變狀態列出分析，見表1。

圖1 三軸壓縮儀器

表1 巖體應力狀態和應變狀態數值

根據表1數值，通過分析巖體的圍壓效應，對其峰值應力σi、殘余應力σr、峰值應變εi和殘余應變εr進行分析，將峰值應力和殘余應力進行擬合，其擬合曲線圖2。

圖2 峰值應力與殘余應力擬合曲線

由圖2可以得到巖體的強度擬合曲線及其變化規律。不難發現，隨著圍壓的上升，應力也在上升，巖體的峰值應力和殘余應力均明顯增大。當圍壓大于20 MPa之后，其應力上升變得緩慢，二者的差值表現出巖體在破壞過程中的應變增量。

巖體的破壞特征關系見圖3。

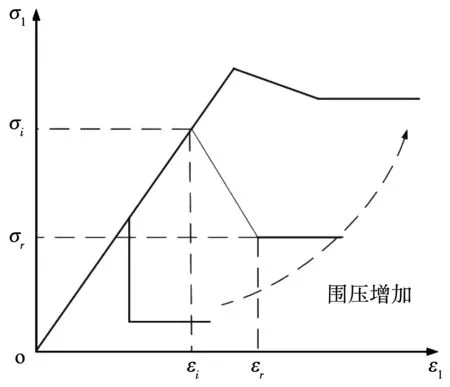
圖3 巖體破壞特征關系模型

由圖3可知，當應力達到峰值時，其曲線為直線；但峰值結束后，迅速回到殘余應力值。由圖3還可以看出，殘余應力值非常平穩。同時，當圍壓增加時，提出了脆性破壞概念，表示其破壞特征，公式如下：

(1)

式中：Eb為圍壓下巖體模量；Δσ為巖體應力掉落值，由σi和σr之差得到；Δε為應變增量，由εr和εi之差得到。

2.3 本構關系模型

本構關系曲線主要為直線彈性-脆性下降-理想狀態3個階段，并且關系曲線需要同時考慮應變、圍壓以及破壞效應。由圖4可以得出3種典型的應力跌落模式，分別對應不改變最小主應力、圓心不變、最短路徑，其中圓心不變為最普遍的運用方法。

圖4 3種典型的應力跌落方式

由圖4可知，其破壞形式非線性存在，由此可得到其應變增量：

(2)

其中，小變形假定為：

Δε=Δεp+Δεe

(3)

增量應力為：

Δσ=σM-σN=DΔεe

(4)

可得：

(5)

滿足：

(6)

由此，將G(σN)與應變率、圍壓和應變增量結合求解，完成應力加載下降過程求解。

3 計算模型

3.1 模型分析

由于引水隧洞所處地形不一，導致其內部構造存在巨大差異性，也導致其巖體力學特性的影響不同。因此，研究引水隧洞在靜動組合下地震響應特征對實際安全問題有指導意義。在地震作用下，引水隧洞的應力狀態見圖5。其中Ph、Pv和Pt分別為引水隧洞的水平荷載、豎向荷載和地震荷載。計算過程中，采用2.3一節提出的本構關系模型進行計算，并考慮多因素影響，計算方案見表2。

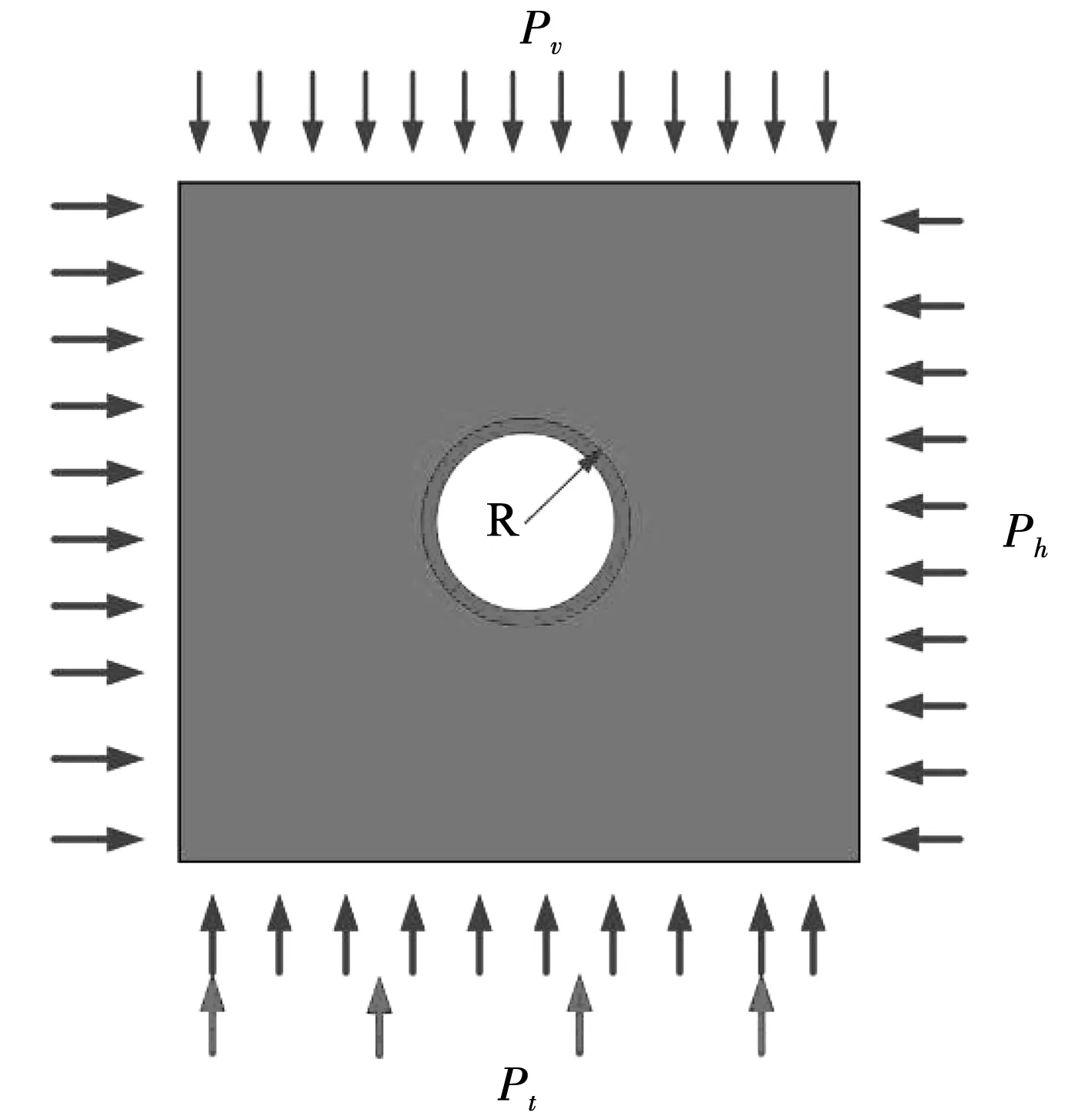
圖5 引水隧洞動靜組合模型分析

表2 計算方案

由表2可知，對3種不同圍壓下的工況進行計算，由此取得參數，并對動靜荷載情況下的地震響應情況進行分析。其中，主要區分在于不同軸壓和不同圍壓以及峰值和進行時間上，考慮到靜荷載作用下地震響應影響與動荷載的剪切波，對引水隧洞的地震響應特性進行分析。

3.2 靜荷載條件

考慮到不同軸壓條件下地震響應情況，并對此進行分析。由表2可知，考慮3種情況下的荷載，控制圍壓為20 MPa。通過模擬可以分析出破壞分布情況與軸壓的變化規律，并且破壞區域主要位于頂拱、底拱和左右腰拱。

其中，當引水隧洞在較高應力狀態下時，會使巖體產生破壞，且損傷面積擴大。但軸壓荷載變大時，剛開始就會產生較大破壞，由此可以得到不同情況下最大應力對比圖，見圖6。

由圖6可知，頂拱與底拱的最大應力均未超過1.0 MPa；但左右腰拱應力值均高于頂拱與底拱的最大應力，并且其值隨著軸壓的上升，應力值也上升，呈正相關。當軸壓達到40 MPa時，頂拱、底拱和左右腰拱均達到最大應力狀態。

圖6 不同軸壓下應力變化曲線

當控制軸壓為20 MPa時，分析3種情況下的圍壓破壞分布情況與圍壓的變化規律，且破壞區域主要位于頂拱、底拱和左右腰拱。由于控制軸壓，巖體的破壞情況分布區域會隨圍壓的變化而變化，并且主要集中在左右腰拱區域。由此說明引水隧洞在受到圍壓作用時，巖體內部空隙部分會被填充，導致巖體的強度得到提升。具體情況見圖7。

圖7 不同圍壓下應力變化曲線

由圖7可知，與軸壓不同的是，當軸壓一定時，圍壓越小，其最大應力反而越大，呈負相關；并且與軸壓一致的是，頂拱和底拱部分的應力值最小。當圍壓達到10 MPa時，應力均達到最大值。但圍壓變化的幅度相較于軸壓變化要緩一些。

3.3 動荷載條件

考慮到不同動荷載條件下地震響應情況，以考慮不同峰值和荷載作用時間為主要因素，由此對其模型進行分析。通過峰值的不同，來研究巖體的破壞趨勢。控制荷載作用時間，時間均為40 ms，當峰值荷載由10 MPa到30 MPa時，破壞范圍由小到劇烈，說明地震峰值荷載會影響巖體動力情況。具體情況見圖8。

圖8 不同峰值下應力變化曲線

由圖8可知，在荷載作用時間不變時，峰值荷載越小，其應力越小，且頂拱和底拱部分的應力值最小；峰值荷載20 MPa與30 MPa的應力差距很大，遠遠大于10 MPa與20 MPa的應力差距，但總體呈正相關。

當控制地震荷載峰值20 MPa，探究不同荷載作用時間對模型的變化規律，作用時間分別為20、40和80 ms。隨著作用時間的增加，巖體的破壞范圍也在增加，但作用時間短，加載情況越大，其產生的應力狀況也越大。具體情況見圖9。

圖9 不同作用時間應力變化曲線

由圖9可知，當地震峰值荷載不變時，荷載作用時間越長，其應力越大；作用時間20 ms與40 ms的差值與40 ms與80 ms的差值相差很大，說明作用時間越長，其應力上升越快，且應力峰值與作用時間呈正相關。

4 結 論

1) 對于引水隧洞地震響應特性主要區分在不同軸壓、圍壓以及峰值和作用時間上，這些因素影響巖體的主要參數變化。

2) 頂拱與底拱的最大應力均未超過1.0 MPa，但左右腰拱應力值均高于頂拱與底拱的最大應力值，

且其值隨著軸壓的上升，應力值也上升，呈正相關。當軸壓一定時，圍壓越小，其最大應力反而越大，呈負相關，且頂拱和底拱部分的應力值最小。當圍壓達到10 MPa時，應力均達到最大值，但圍壓變化的幅度相較于軸壓變化要緩一些。

3) 荷載作用時間不變時，峰值荷載越小，其應力越小，且頂拱和底拱部分的應力值最小；峰值荷載20 MPa與30 MPa的應力差距遠遠大于10 MPa與20 MPa的應力差距，但總體呈正相關。當地震峰值荷載不變時，荷載作用時間越長，其

應力越大；且作用時間20 ms與40 ms的差值與40 ms與80 ms的差值相差較大，說明作用時間越長，其應力上升越快，且應力峰值與作用時間呈正相關。