基于優化多重索引的橢圓球面波函數多載波索引調制解調方法

王紅星 張力凡 陸發平 康家方 劉傳輝 張 磊

(海軍航空大學 煙臺 264001)

(中國人民解放軍91206部隊 青島 266109)

1 引言

隨著移動通信業務需求的迅速增長，如何提高信息傳輸的頻譜效率和能量聚集度已成為現階段通信研究的熱點問題[1–3]。近年來，針對如何提高頻譜效率和能量聚集度，一系列解決方案相繼被提出：統一濾波多載波(Universal Filtered Multi-Carrier, UFMC)[4]、廣義頻分復用(Generalized Frequency Division Multiplexing, GFDM)[5]、基于橢圓球面波函數的多載波調制(Multi-Carrier Modulation based on Prolate Spheroidal Wave Functions, MCM-PSWFs)[6,7]等。其中，相比于UFMC,GFDM, MCM-PSWFs將具有完備正交性、時域奇偶對稱性和最佳時頻能量聚集性等優良基礎特性的PSWFs函數[8,9]作為基礎信號，具有信號波形設計靈活、高能量聚集性以及高系統頻帶利用率(Spectral Efficiency, SE)[8]的優勢，非常符合下一代通信系統對能量聚集度的需求，具有巨大的應用潛力，極具有應用前景[6,7]。

為進一步提升MCM-PSWFs的系統頻帶利用率，研究團隊將索引調制技術(index modulation)[10]引入MCM-PSWFs，提出了基于信號分組優化的PSWFs多載波調制方法(Multi-Carrier Modulation based on PSWFs with Signal Grouping Optimization, MCM-PSWFs-SGO)[11]。該方法首先對PSWFs信號進行分組優化，再利用信號索引、脈沖幅度調制兩個維度進行信息映射，充分發揮了索引調制技術能夠大幅提高信息傳輸頻譜效率的特點，又兼具PSWFs函數信號波形設計靈活、高能量聚集性的優勢，具有高能量聚集度、高頻譜效率的優點。盡管如此，由于部分未被激活的子載波沒有用來傳遞信息，MCM-PSWFs-SGO仍有部分頻譜資源可進一步被利用，這在一定程度上限制了其系統頻帶利用率的提升。其后，研究團隊又引入了雙模索引調制的思想，提出了雙模PSWFs多載波索引調制解調方法(Multi-Carrier index Modulation based on PSWFs with Dual-Mode, DMMCM-PSWFs)[12]，該方法將MCM-PSWFs-SGO中保持靜默的子載波加以利用，傳輸由第2星座圖映射的調制符號，在不改變峰均功率比和能量聚集度的前提下，以犧牲部分復雜度為代價，有效提升了系統頻帶利用率和大信噪比下的誤碼性能。但是，無論是MCM-PSWFs-SGO還是DM-MCMPSWFs，由于其信號索引方案維度的限制，只對子載波數n進行了1次排列組合的運算，系統頻帶利用率仍有提升空間。2017年，華南理工大學Wen等人[13]提出了多模索引調制技術(Multiple-Mode Orthogonal Frequency Division Multiplexing with Index Modulation, MM-OFDM-IM)，其使用n個星座圖的階乘作為信號索引方案，能夠使調制符號的排列組合數最大化，大幅提升系統頻帶利用率。但該方法仍然存在提升空間：若不使用I/Q支路分別傳輸信息，能夠保證誤碼性能不損失太多，但系統頻帶利用率提升有限；若使用I/Q支路分別傳輸信息，利用脈沖幅度調制(Pulse Amplitude Modulation, PAM)方式進行調制符號映射，雖然能夠大幅提升系統的頻帶利用率，但隨著n的增大，MM- OFDM -IM的誤碼性能在高斯白噪聲信道下會受到較大的影響。

因此，如何改變原有的雙模信號索引方案，拓展信號索引維度，能夠在達到頻帶利用率進一步提升的同時，盡可能減小隨著子載波數n的增大所導致的由于最小歐氏距離((Minimum Euclidean Distance, MED)大幅減小而帶來的誤碼性能的急劇惡化，使多模索引調制的思想在加性高斯白噪聲(Additive White Gaussian Noise, AWGN)信道下能夠被更好地運用，實現AWGN信道下更優系統頻帶利用率提升和更少誤碼性能損失，這對基于PSWFs的多載波索引調制的發展有著重要的意義。

本文提出一種基于優化多重索引的橢圓球面波函數多載波索引調制解調方法(Multi-Carrier index Modulation based on Prolate Spheroidal Wave Functions with Better multIple-Mode,BIM-MCM-PSWFs)。在原有利用雙星座圖映射的DM-MCM-PSWFs的基礎上引入由更外圍星座點組成的第3星座圖，進一步增加調制符號的組合數，在子載波數n較大的情況下，以少量犧牲誤碼性能和系統復雜度為代價，對頻帶利用率進行進一步的提高。

2 BIM-MCM-PSWFs調制解調與檢測方法

DM-MCM-PSWFs系統頻帶利用率提升受限的原因在于，在進行信號索引方案的設計過程中，僅對每組子載波進行了1次排列組合的運算，頻譜效率尚有提升空間。MM-OFDM-IM存在的問題在于，由于每組子載波的信號索引方案由與子載波數量相等個數的星座圖的全排列組成，在每組子載波數較大的情況下，引入過多的星座點，導致最小歐氏距離大幅減小，雖然提高了系統頻帶利用率，但在AWGN信道下，誤碼性能急劇惡化，并不能得到頻帶利用率和誤碼性能的更優權衡。因此，如何在不引入過多星座點的基礎上，增加調制符號的組合數，是以更小的誤碼性能的犧牲，進一步提升DM-MCM-PSWFs系統頻帶利用率的關鍵。

2.1 BIM-MCM-PSWFs調制方法

圖1(a)給出了BIM-MCM-PSWFs發射端原理框圖。該方法引入第3星座圖，首先利用第3星座圖對一個子載波進行調制符號的映射，再利用剩余兩個星座圖對剩余子載波進行調制符號的映射，同時，采用I/Q兩個支路進行分別傳輸，且采取相同的信號索引結構。

考慮到PSWFs信號分組數、每組信號路數、調制星座圖進制數以及激活信號路數等參數直接決定系統整體性能，需要依據可用時頻資源大小、系統整體性能需求，進行整體的設計和選擇[11]。為便于分析，假設可用時寬為T(s)、 帶寬為B(Hz)，信號分組數g、每組PSWFs信號路數為n、每組1次選擇的信號路數為k，每組2次選擇的信號路數為m，3種星座圖的調制階數相同，且均為M。

如圖1(a)所示，將輸入2j(bit)待傳信息比特平均分為g組，每組包含p′= 2j/g=pI+pQ(bit)信息，其 中pI=pQ=p,pI=pα,I,1+pα,I,2,pQ=pα,Q,1+pα,Q,2,α∈[1,g]，pα,I/Q,1為I/Q支路信號索引部分攜帶信息量，pα,I/Q,2為3個星座圖產生的調制符號攜帶的信息量；而后，分別進行3個星座圖的調制與比特信息映射，生成調制符號，并產生BIMMCM-PSWFs調制信號。

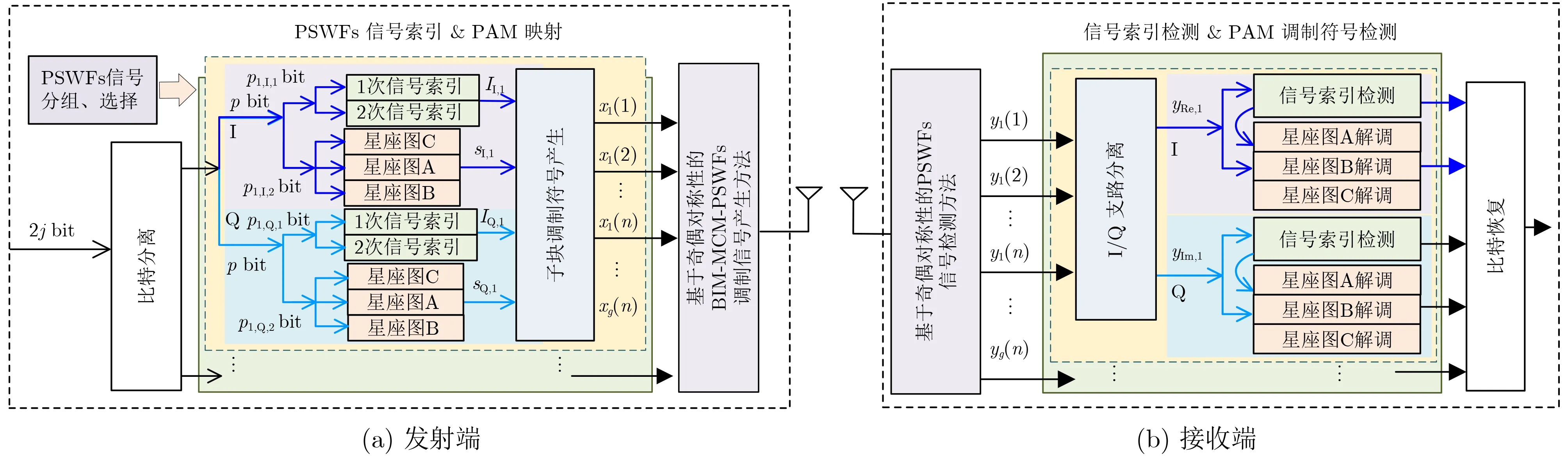
圖1 BIM-MCM-PSWFs原理框圖

(1)星座圖設計與比特信息映射：與DM-MCMPSWFs不同，BIM-MCM-PSWFs將原有的雙星座圖調制方法變更為3星座圖調制，首先由星座點位于最外圍的第3星座圖對每組PSWFs信號路數n中的1個進行調制符號映射，再由其他兩個星座圖對剩余子載波進行調制符號映射，如圖2所示。為保證接收端能夠順利解調和檢測出信號索引比特所攜帶的信息，需對選取的3個星座圖有所區分，因此，選擇的3個星座圖還必須滿足互不重疊的關系。值得注意的是，只要滿足所提方法對星座圖的要求，任意的3個星座圖均可作為選取的對象，但根據不同星座圖的星座點分布與最小歐氏距離的差異，星座圖的選取不同也會導致系統性能發生變化。因此，在對星座圖進行選取時，應以星座點間最小歐氏距離最大化為出發點，對星座圖進行擇優選取。為便于仿真分析，本文僅給出一種星座圖選取方式，即為了方便分析比較，本文采取了與對比方法“基于信號分組優化的PSWFs多載波調制方法”及“雙模橢圓球面波多載波調制解調方法”類似的特殊的PAM星座圖，如圖3所示。

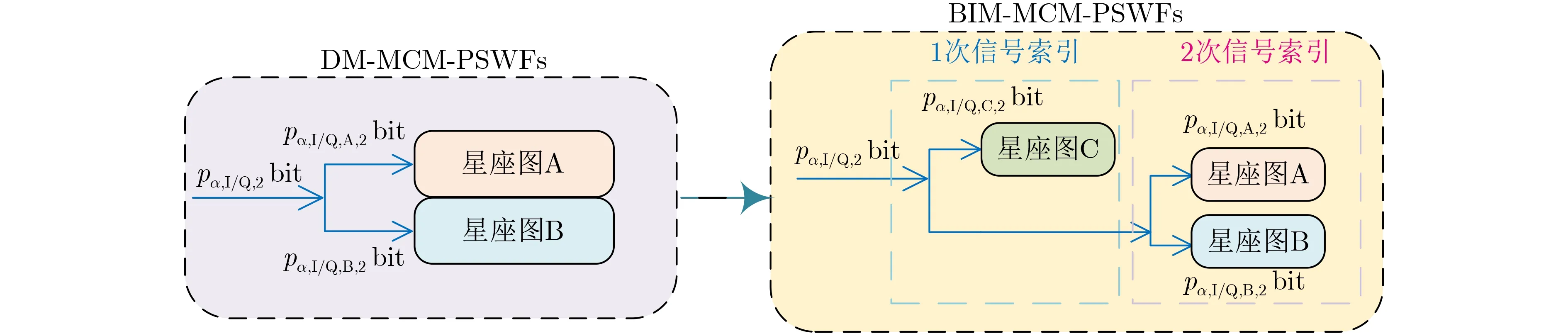
圖2 BIM-MCM-PSWFs與DM-MCM-PSWFs映射原理對比

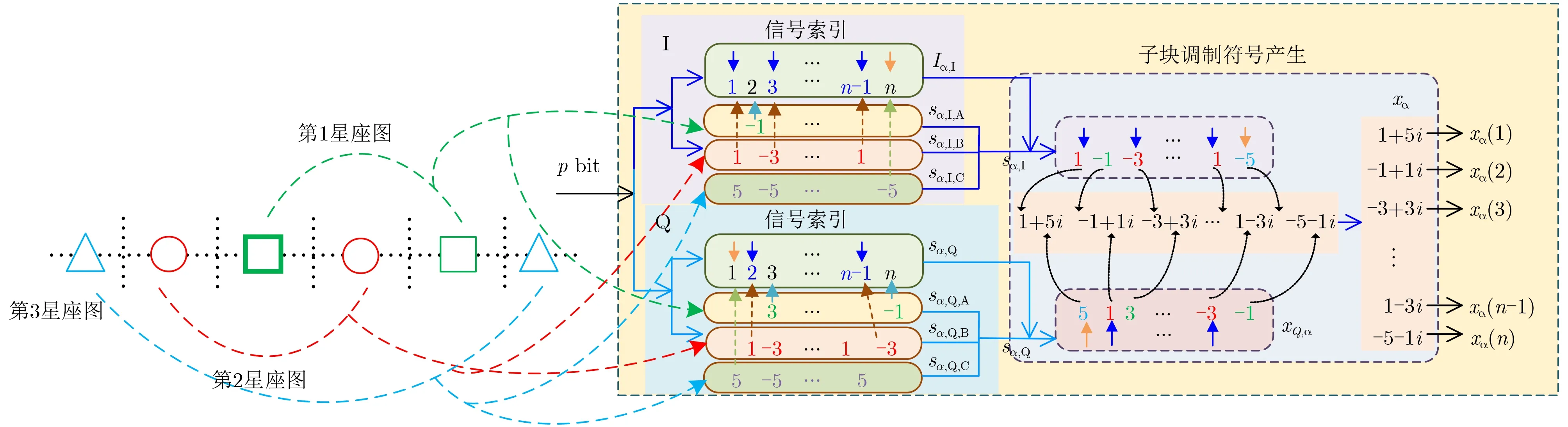
圖3 BIM-MCM-PSWFs調制符號加載過程

2.2 BIM-MCM-PSWFs調制信號的解調與檢測方法

圖1(b)給出了調制信號的解調與檢測的原理框圖。與DM-MCM-PSWFs相同，采取基于極大似然(Maximum Likelihood, ML)[12]的信號索引檢測方法，對所有可能的信號索引方案進行遍歷，以最小化接收信號與樣本信號之間的歐氏距離，恢復出信號索引方式，即

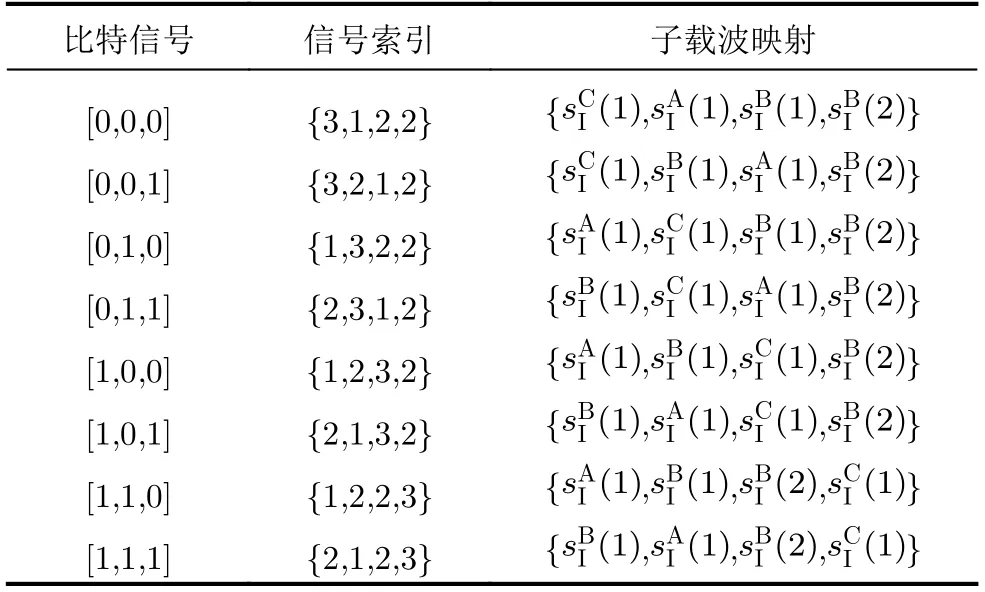
表1 n=4, k=3, m=2時BIM-MCM-PSWFs的一種映射方案

值得注意的是，由于所提方法需要進行額外星座圖的解調與檢測處理，其調制信號解調與檢測的計算復雜度將高于DM-MCM-PSWFs和采用基于順序統計量的索引調制信號檢測方法[14]的MCMPSWFs-SGO，該部分問題將于第3節系統性能分析的內容中進行討論。

3 系統性能分析

前期研究團隊已經對雙模PSWFs多載波索引調制方法進行了分析，相對于基于PSWFs的正交多載波調制方法，雙模PSWFs多載波索引調制方法具有更優的系統誤碼性能與頻帶利用率。因此，本節從系統頻帶利用率、系統誤碼性能、信號索引檢測復雜度3個方面，重點分析所提方法與雙模PSWFs多載波索引調制方法、基于信號分組優化的PSWFs多載波調制方法的性能差異。

3.1 系統頻帶利用率分析

(2)與基于信號分組優化的橢圓球面波多載波調制解調與檢測方法(MCM-PSWFs-SGO)相比：MCM-PSWFs-SGO的系統頻帶利用率由c ?l,M,n,k共同決定，而所提方法的系統頻帶利用率則由c ?l,M,n,k,m共同決定。因此，當M相同時，根據式(8)，所提方法的系統頻帶利用率將大于MCM-PSWFs-SGO。n=9,k=8,m=4時，以BER犧牲了1.88 dB為代價，SE提升了53.9%，如表2所示。當MCM-PSWFs-SGO采用更高階的星座圖進行調制符號映射時，在對參數進行優選的情況下，所提方法能夠取得頻帶利用率與誤碼性能的雙重提升。當M=4時，SE與BER分別提升了28.4%和1.76 dB。

表2給出了帶寬為B= 1.44 MHz，頻率間隔為F= 15k Hz, B ER=10?5時不同參數條件下，3種調制方法的系統頻帶利用率對比。其中，l= 4,ρ表示相比于另外兩種調制方法，所提方法對系統頻帶利用率的提升。

表2 不同多載波調制方法系統頻帶利用率

此外，前文中提到，PSWFs載波信號的選擇過程也是本文所提方法的關鍵環節，在對載波信號進行優選的情況下，能夠獲得最優的系統頻帶利用率，為更詳細地體現PSWFs載波信號選取的不同對本文所提方法系統頻帶利用率的影響，表3給出了在相同帶寬B= 1.44 MHz， 相同頻率間隔F= 15 kHz情況下不同PSWFs載波信號選取對所提方法系統頻帶利用率的影響。圖4給出了兩種載波信號選取情況下對應的功率譜。

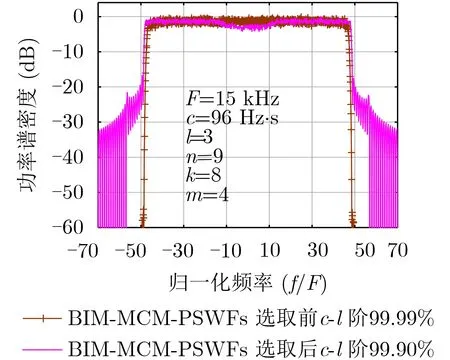
圖4 BIM-MCM-PSWFs調制信號功率譜

表3 不同多載波調制方法系統頻帶利用率

3.2 系統誤碼性能分析

鑒于MED能夠反映調制方法的誤碼性能，本節選用MED對不同調制方法的系統誤碼性能進行分析。值得注意的是，由于所提方法使用了3個星座圖，且第3個星座圖由外圍星座點所組成，其MED略大于剩余兩個星座圖的MED，并且由于在每組子載波中，只有少量子載波傳輸由第3星座圖映射的調制符號，其MED對系統誤碼性能影響很小，故其MED在此處不參與討論。圖5給出了未進行信道編碼情況下的不同調制方法系統誤碼性能。其中，BIM-MCM-PSWFs采用如圖3所示的星座圖。當每比特信息對應的能量為Eb時，不同調制方法的MED可表示為

由式(11)可知，所提方法的最小歐氏距離要小于DM-MCM-PSWFs，但隨著n的增加，二者的最小歐氏距離逐漸逼近，在n較大的情況下，二者的最小歐氏距離幾乎相同，這表明所提方法能夠以較小的BER犧牲為代價，獲得系統頻帶利用率的提升。圖5給出了不同調制方法系統誤碼性能，可以看出子載波數n=9的性能要好于n=8的性能，在BER=10–5時，以更小的信噪比犧牲換取了更多的系統頻帶利用率的提升。如當BER=10–5, n=9時，所提方法相比于DM-MCM-PSWFs，誤碼性能犧牲了0.70 dB，系統頻帶利用率提升了20.1%，如圖5(b)所示。

(2)與基于信號分組優化的橢圓球面波多載波調制(MCM-PSWFs-SGO)相比：由式(9)可知，所提方法與MCM-PSWFs-SGO的MED比值為

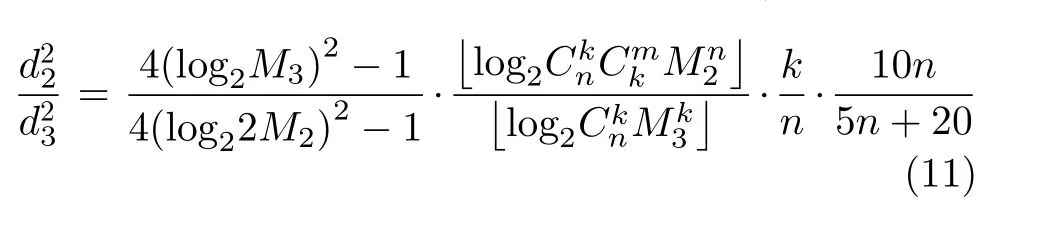
同樣，為保證MCM-PSWFs-SGO與所提方法的系統頻帶利用率相同，MCM-PSWFs-SGO選取4PAM為星座圖，并且令BIM-MCM-PSWFs中的k=n–1，則式(11)可以化簡為

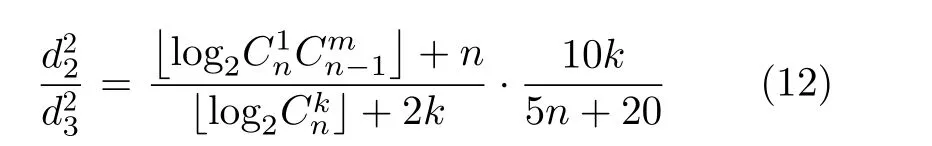
由式(12)可以得出，在n,k較大，即高頻譜效率的情況下，所提方法的MED大于MCM-PSWFs-SGO，即擁有更優的誤碼性能。如當BER=10–5,n=9時，所提方法相比于MCM-PSWFs-SGO誤碼性能和系統頻帶利用率分別提升了1.76 dB, 28.4%，如圖5(b)所示。

除重點分析和對比了所提方法與DM-MCMPSWFs及MCM-PSWFs-SGO的頻帶利用率和誤碼性能以外，圖5(b)還給出了選取后c-l階PSWFs函數作為載波信號時的誤碼性能，結合3.1節中對該情況下頻帶利用率的分析可知，PSWFs載波信號的選取對系統誤碼性能的影響很小，對系統頻帶利用率的影響較大，因此，為取得更優的系統整體性能，對PSWFs信號進行優選是所提方法的核心基礎。

圖5(c)、圖5(d)還分別給出了所提方法與基于廣義信號索引的橢圓球面波函數多載波調制解調方法(MCM-PSWFs with GIM, MCM-PSWFs-GIM)[15]及廣義 OFDM-IM(Generalization OFDM-IM,OFDM-GIM)[16]的頻帶利用率和誤碼性能的對比，從圖中可以看出，相較于MCM-PSWFs-GIM，所提方法以犧牲部分誤碼性能為代價，換取了頻帶利用率的大幅提升，在BER=10–5時，以犧牲了0.75 dB誤碼性能為代價，系統頻帶利用率提升了30.2%；相較于OFDM-GIM，所提方法在大信噪比情況下獲得了誤碼性能和頻帶利用率的雙重提升，在BER=10–5時，誤碼性能和系統頻帶利用率分別提升了1.0 dB，30.2%。

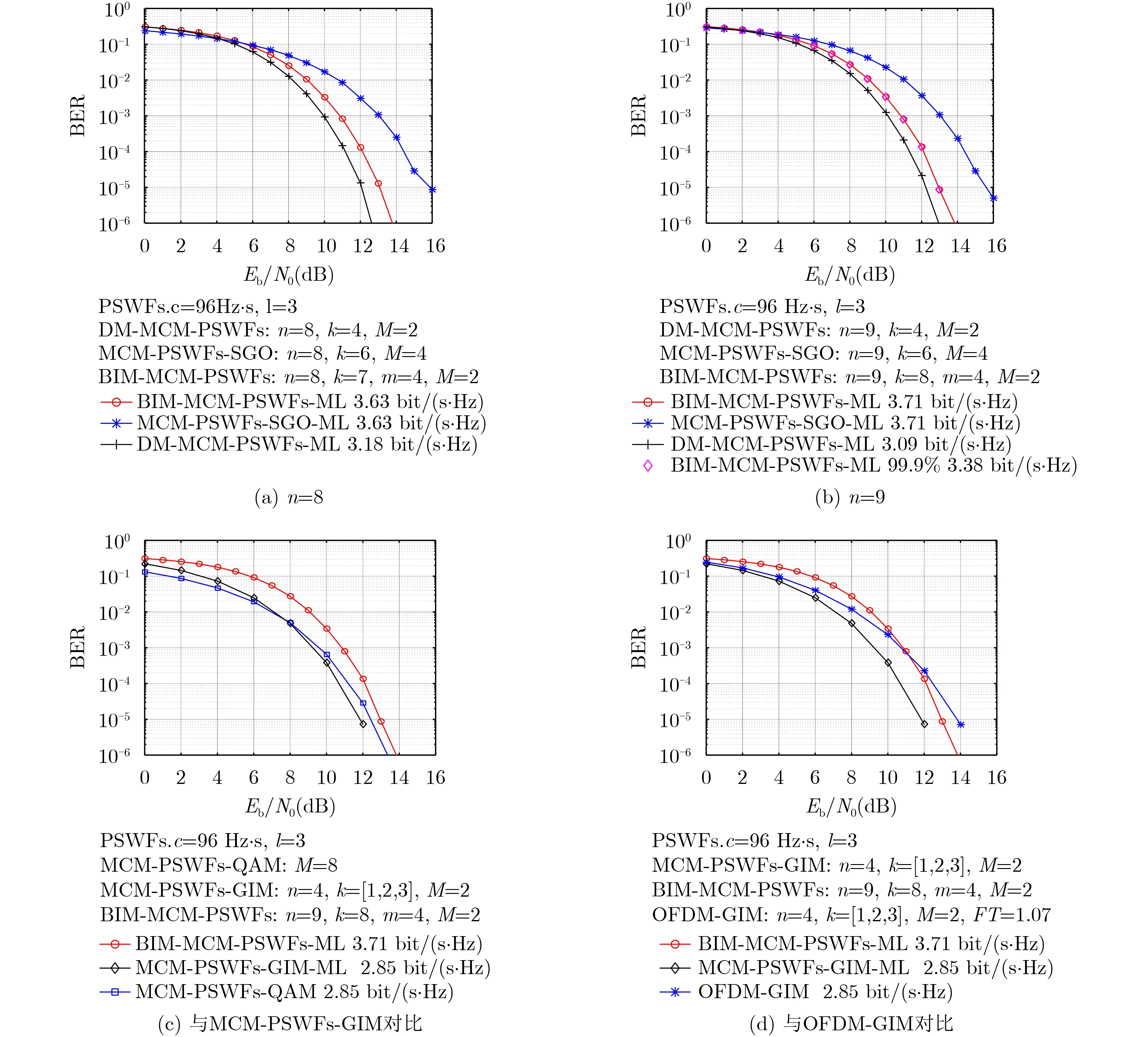
圖5 不同調制方法系統誤碼性能

3.3 系統信號索引檢測復雜度分析

現對比所提方法與DM-MCM-PSWFs的信號索引檢測復雜度。表4給出了帶寬為B= 1.44 MHz，頻率間隔為F= 15 kHz的不同參數條件下，所提方法與DM-MCM-PSWFs兩種調制方法的信號索引檢測乘法復雜度，其中l= 4。

表4 信號索引檢測乘法運算量

當兩種調制方式均使用ML對信號索引進行檢測時，所提方法的計算復雜度略高于DM-MCMPSWFs。因此，結合前兩節關于3種調制方法頻帶利用率與誤碼性能的分析可知，所提方法是以較高的計算復雜度和部分誤碼性能換取了系統頻帶利用率的提升。

4 結束語

本文提出基于優化多重索引的橢圓球面波函數多載波索引調制解調方法，在原有的利用雙星座圖映射的DM-MCM-PSWFs的基礎上引入由更外圍星座點組成的第3星座圖，進一步增加調制符號的組合數，在n較大的情況下，實現了系統頻帶利用率和大信噪比下的誤碼性能的雙重提升。雖然仍存在較高的計算復雜度，但這是當前硬件條件和計算能力可以承受的。相比于DM-MCM-PSWFs,MCM-PSWFs-SGO，本文具有更優的系統整體性能，有望為下一代通信系統提供更加靈活、高效的調制方法，實現更高頻譜效率與能量聚集度的信息傳輸。

值得注意的是，本方法仍有進一步提升的空間，如何選取最優的星座圖，在對SE的提升不變的情況下，使損失的BER進一步降低，是本文下一步研究的重點。此外，由于本方法在低信噪比下的誤碼性能仍有提升的空間，因此，如何對信號索引檢測進行優化，進一步提升系統整體誤碼性能，并且結合具體場景，分析系統性能，也是后續將要進行的內容之一。