立體交叉隧道爆破振動影響因素正交試驗研究

戴 軼， 劉家明， 張俊儒， 王智勇

(西南交通大學土木工程學院交通隧道工程教育部重點實驗室，四川成都 610031)

隨著我國國民經濟的發展，交通設施需求日益增加，新建隧道數量逐年增多。隨著眾多交通隧道復線工程的修建，由于地質條件、既有建(構)筑物的限制以及地下空間綜合開發的需求，不可避免地會出現許多近接或者交叉的現象。

立體交叉隧道作為近接隧道的一種，其圍巖及襯砌的變形、應力變化都有著自身的規律特點[1]。目前，國內外學者在這方面已有了廣泛的研究，同時也取得了一定的研究成果。龔倫等[2]結合新建隧道下穿既有隧道工程實例，采用數值模擬的方法，對既有鐵路隧道受下穿引水隧洞施工的影響和鐵路隧道結構的安全對策進行了研究。游步上等[3]利用FLAC3D程序分析隧道交叉段的變形行為，探討不同應力場與不同巖石強度等參數對隧道交叉段應力變化情況。趙東平等[4]借助FLAC3D模擬計算了小凈距空間交叉隧道的爆破振動，并結合GB 6722-86《爆破安全規程》中的安全控制振速，劃分了新建隧道爆破開挖的影響范圍。劉鎮等[5]采用三維彈塑性有限元方法對上下交叉隧道盾構施工進行了分析，針對圍巖條件及間距，探究新建正交盾構隧道下穿施工對既有隧道沉降的影響。王明樂等[6]以新建鐵路隧道為背景，采用三維彈塑性有限元方法，對交疊隧道進行數值模擬，從而進行施工方案優化。靳曉光等[7]通過三維彈塑性有限元方法，結合實際工程，分析了橫通道不同施工方案和動態施工過程對主隧道圍巖與初期支護結構力學行為的影響。王海龍等[8]以新建京張高鐵草帽山隧道下穿既有唐呼重載鐵路北草帽山隧道交叉工程為背景，結合爆破振速的現場實測和經驗公式理論分析，提出爆破施工方案。上述研究多是針對交叉隧道的靜力影響因素，而立體交叉隧道工程中新建隧道對既有隧道爆破振動的動力學的影響因素方面的研究相對較少。

然而當立體交叉隧道凈距較小時，新建隧道開挖產生的爆破振動難免會給予周邊既有隧道的支護結構、內部設施以及所承擔的交通營運造成一定程度的影響，甚至威脅到安全性。如日本的荻津公路隧道以及意大利的 LocooColio 公路隧道，國內的西康線響水溝隧道、流潭隧道等，都出現過由于新舊隧道凈距較小而導致既有隧道襯砌結構開裂、剝落等危及行車安全等現象[9]。因此，研究立體交叉隧道不同爆破振動因素對既有線的不利影響，探究其內在聯系，顯得尤為重要。

在相關文獻調查中，發現立體交叉隧道爆破施工存在多方面的影響因素：凈距、圍巖級別、埋置深度、交叉角度、開挖方法和支護方式等[10-12]。基于以上研究背景，本文基于數理統計學和正交性試驗原理，設計多種正交試驗工況，探究新建隧道對既有隧道爆破振動動力影響。通過試驗，對既有線隧道正交段襯砌不同位置的振動速度進行極差分析，擬得到不同影響因素下新建隧道爆破振動對既有隧道的動力影響結果，可為立體交叉隧道設計施工提供一定理論依據。

1 試驗方案設計

根據對立體交叉隧道爆破振動影響因素的文獻調查發現，對既有隧道產生爆破振動影響的因素眾多，其中部分影響因素相較而言敏感性較低。為此，本文主要針對4種重要影響因素進行研究，即：凈距、圍巖級別、埋深和交叉角度，主要影響因素及水平如表1所示。

從表1可以得到：立體交叉隧道對既有隧道的爆破振動影響為4個非支護因素，每種因素存在4個水平因子。則可將其視作一個的44正交試驗，選取L16(45)的正交試驗表，共設計了16種數值模擬試驗工況，將最后一列設置為空列得到正交試驗工況，如表2所示。

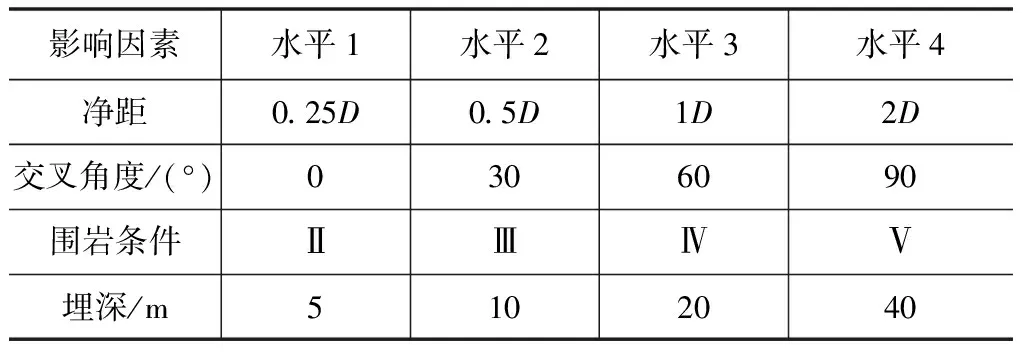
表1 主要影響因素及水平

表2 正交試驗工況設計

2 數值模擬計算

2.1 計算假定

采用有限差分數值計算方法進行3D計算，考慮交叉隧道相互影響長度[13]，16種試驗工況數值模型長度取80 m，寬度取50 m，深度根據計算工況以及圣維南原理，并滿足幾點假定：

(1)圍巖為彈塑性材料，服從Mohr-Coulomb屈服準則；初支、二襯為彈性材料。

(2)16種計算工況均為新建隧道下穿既有隧道。

(3)16種計算工況均采用上下臺階法進行靜力計算，計算至交叉斷面時進行動力計算，監測斷面取既有隧道與新建隧道的交叉斷面，監測點均設置在既有隧道內。

(4)模型兩側及底部均限制法向位移，地表為自由面。

(5)由于隧道下臺階爆破時臨空面較大，爆破振動對既有線的影響遠遠小于上臺階爆破時的影響[14]。因此，數值計算只分析上臺階爆破振動影響。

2.2 爆破荷載

新建隧道開挖爆破荷載利用圣維南原理，采用等效荷載施加方式，將爆破柱狀荷載建模方法等效成面荷載，即將作用在炮孔壁上的孔狀爆破荷載等效成面荷載，這種等效方法不僅不需對掌子面炮孔建模，且計算容易收斂，提高計算效率。

將爆破荷載簡化為由升壓段和降壓段組成的三角型脈沖荷載，荷載峰值應力Pmax[15]由式(1)進行求解。

(1)

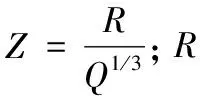
爆破荷載的升壓段時間t0取10 ms，降壓段時間t1取90 ms，總爆破時間為100 ms[16]。三角型脈沖荷載時程曲線如圖1所示。

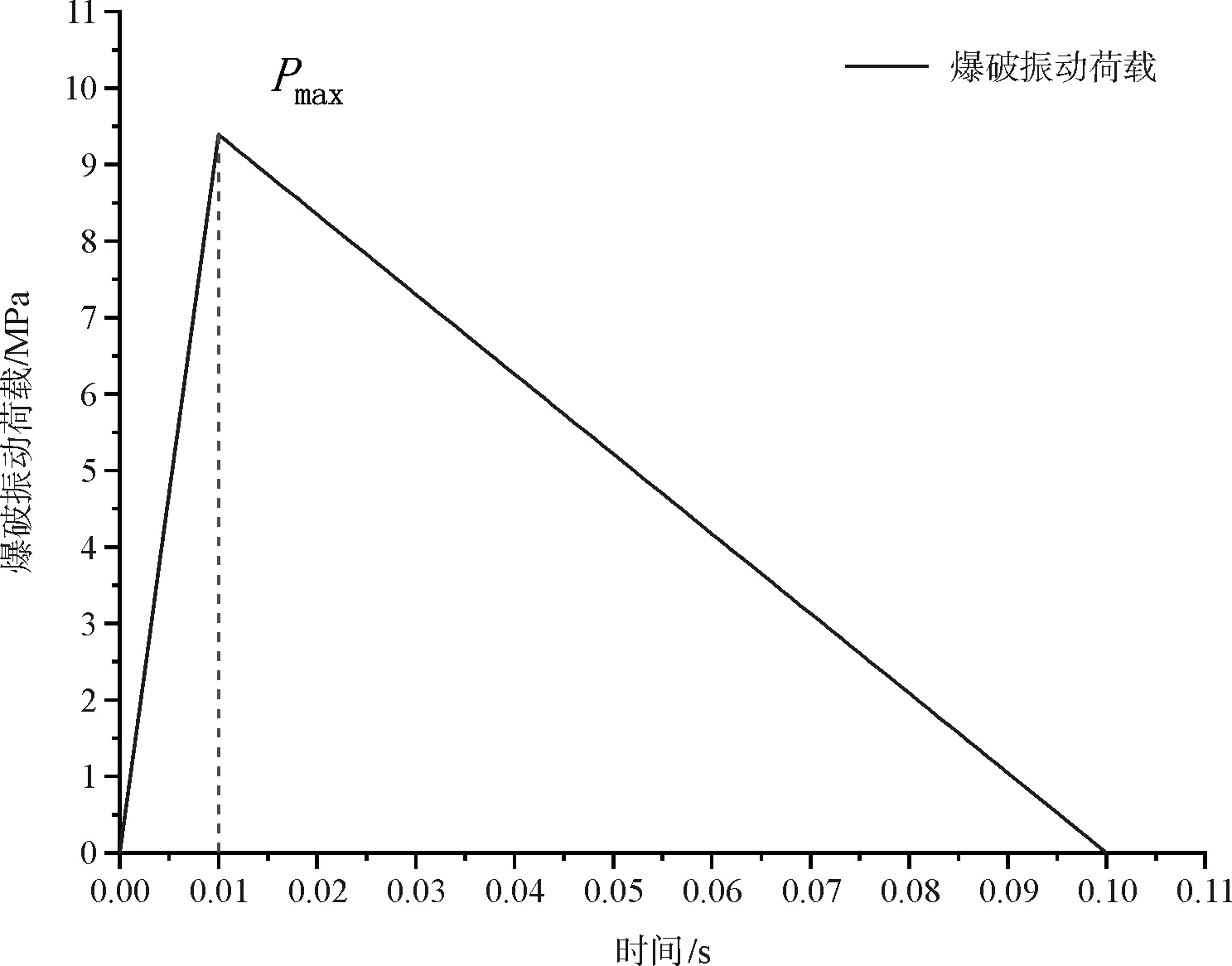
圖1 三角型脈沖荷載時程曲線

2.3 材料參數

開始進行動力分析時，一般將圍巖的參數進行一定的修正，圍巖的變形模量按照Ed=8.7577ES0.5882修正[17]，泊松比按照νd=0.8νs修正[18]。主要材料參數參照相關手冊選取[19]，如表3所示。圖2和圖3分別為部分計算工況模型和既有隧道監測點布置。

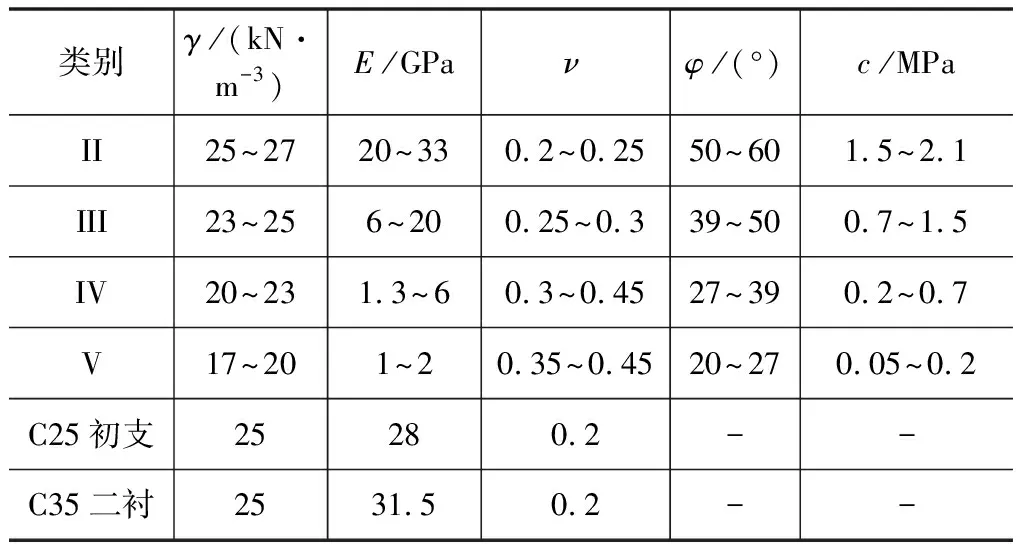
表3 圍巖及支護材料物理力學參數

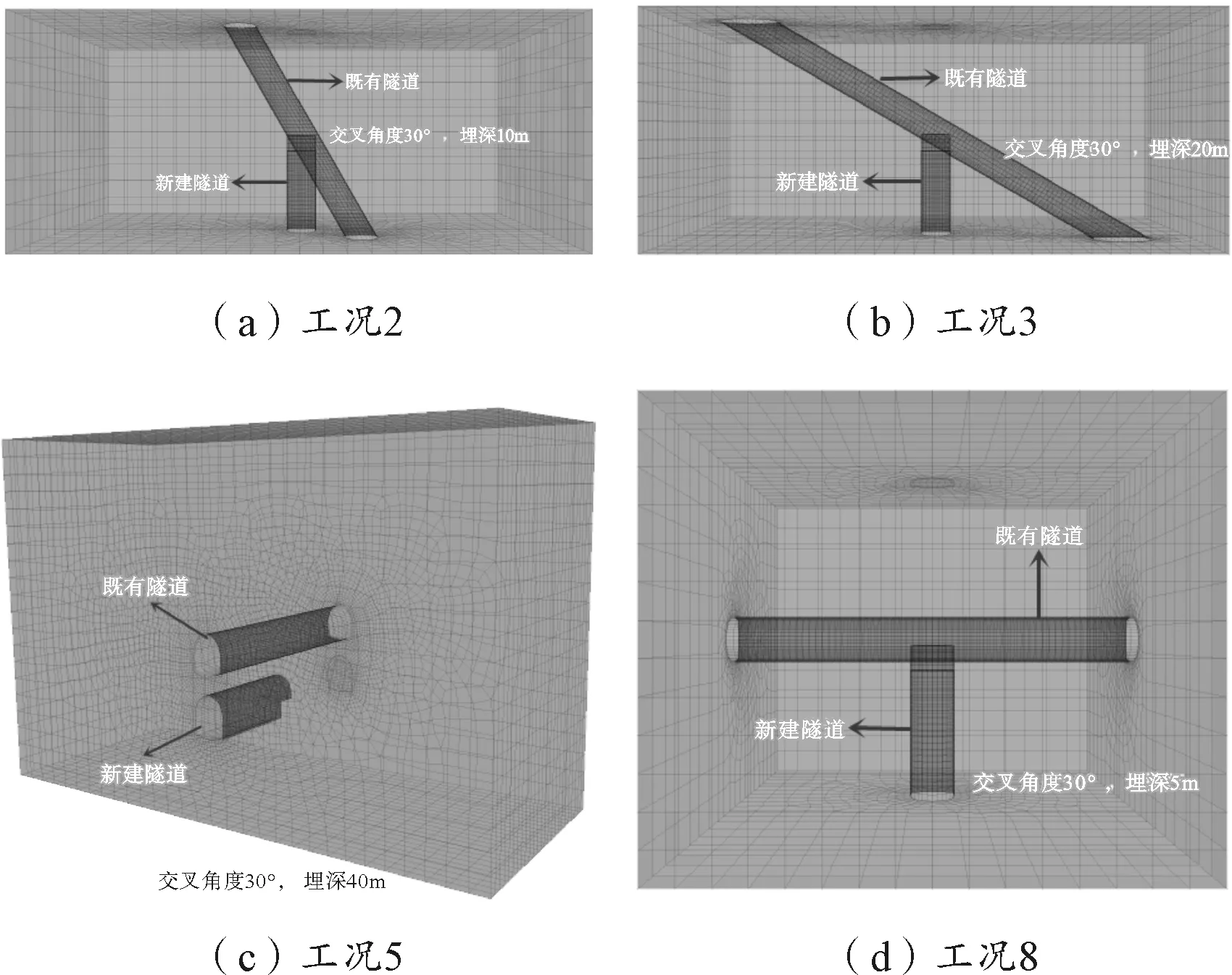
圖2 部分計算工況模型

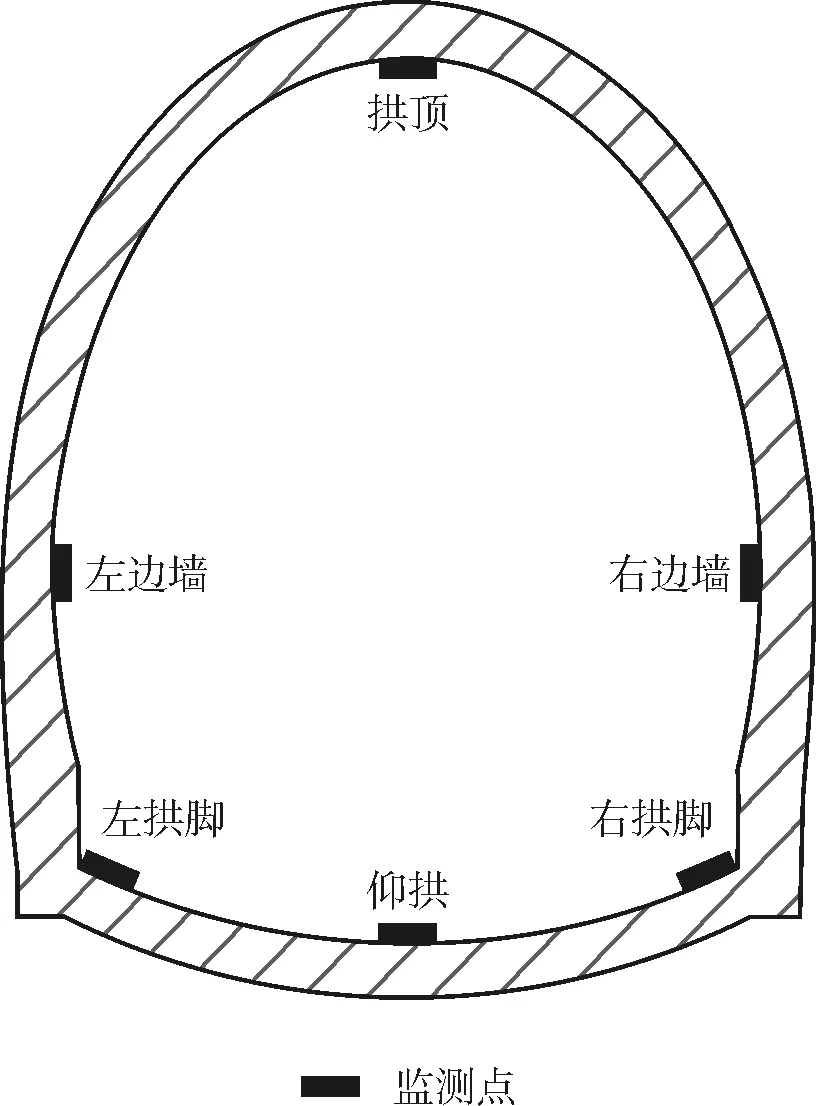
圖3 既有隧道監測點布置

3 試驗結果分析

3.1 計算結果

表4為各試驗工況下，數值模擬動力計算階段過程中，既有線隧道距離新建隧道爆破面最近的監測斷面的拱頂、邊墻、拱腳以及仰拱的最大振動速度。

爆破對既有結構的破壞因素眾多，但目前已有的研究結果表明：建筑結構破壞程度受結構關鍵點振動速度的影響較大，以質點的峰值振速作為爆破振動安全的評定標準既準確又相對簡單[20]。因而，計算結果分析僅對監測斷面關鍵部位爆破振速進行(表4)。

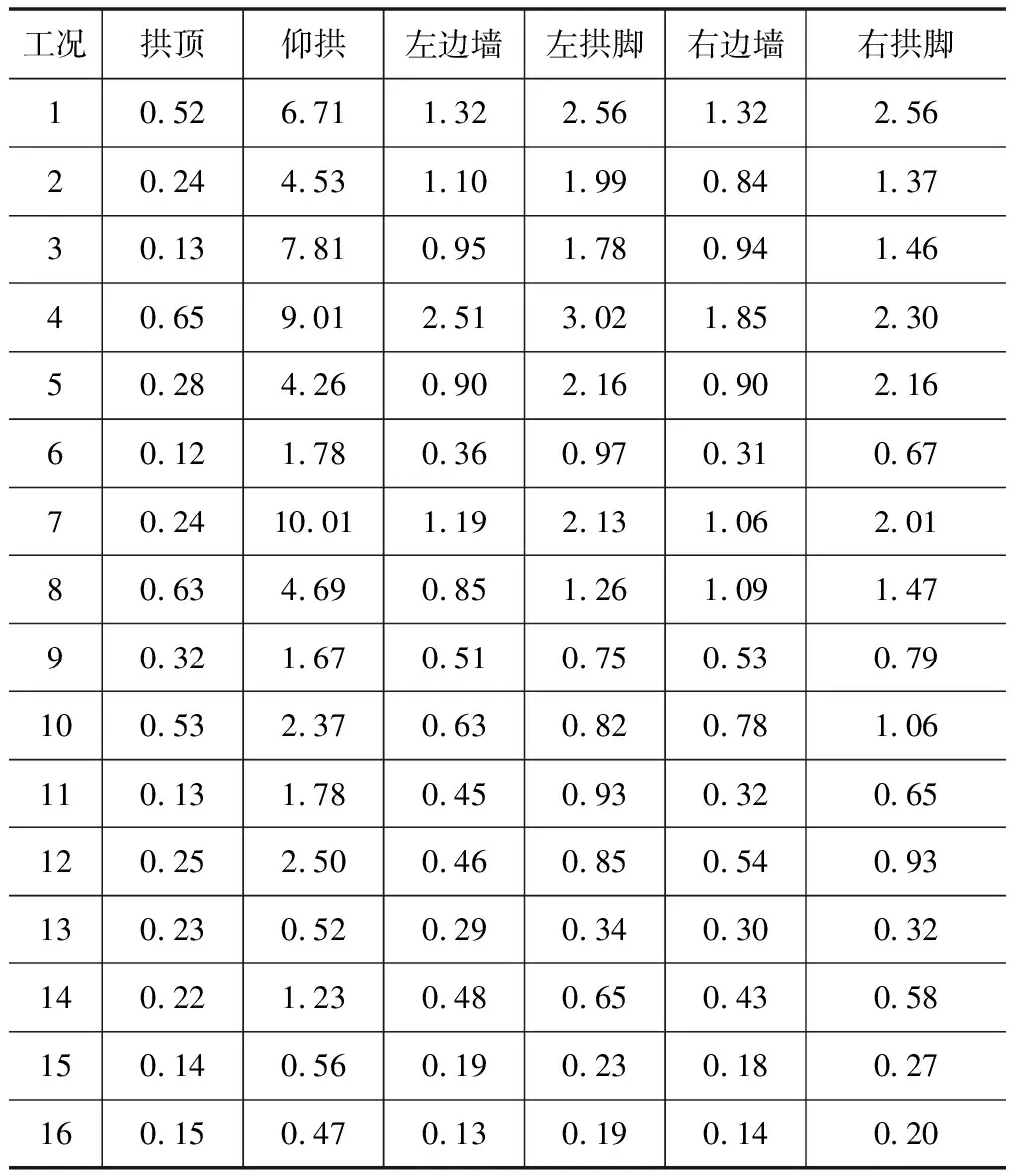
表4 振速數值計算結果 單位：cm/s

3.2 結果分析

目前，對于正交試驗結果分析方法，一是極差分析法；另一種方法是方差分析法。其中，極差分析法又稱為直觀分析法，具有直觀形象、通俗易通的特點，是正交試驗結果分析最常用的方法之一。因此，本文遂采用極差分析法，根據各計算工況下極差Ri的大小，判斷各因素對試驗結果的影響大小。判斷原則：極差愈大，所對應的因素愈重要；由此可以確定出主、次要因素的排序。試驗分析結果見表5和表6。

表5 各特征位置在各因素下的振速極差Ri 單位：cm/s

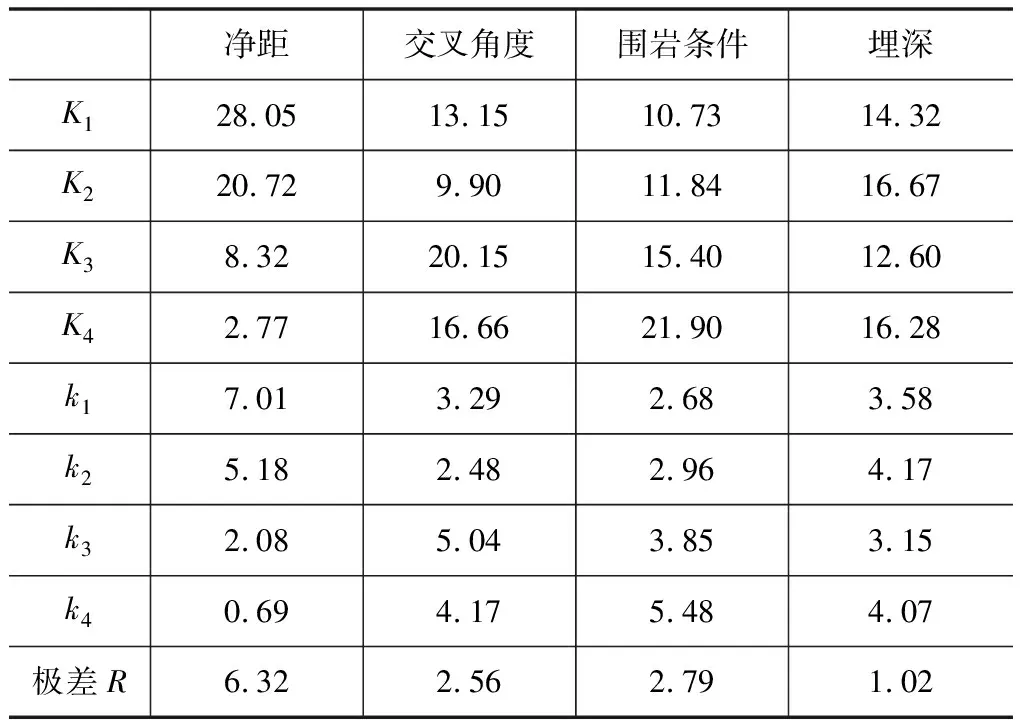
表6 仰拱極差分析 單位：cm/s

圖4繪制了既有隧道各測點振速極差與各影響因素曲線圖。由圖可知，各影響因子對立體交叉處既有線監測斷面仰拱振速極差敏感性排序為：凈距(6.32 cm/s)、圍巖條件(2.79 cm/s)、交叉角度(2.56 cm/s)、埋深(1.02 cm/s)，其中凈距為重要影響因素，交叉角度和圍巖條件為次要影響因素，埋深為一般因素。各影響因子對立體交叉處既有線監測斷面拱頂振速極差敏感性排序為：埋深(0.27 cm/s)、交叉角度(0.26 cm/s)、凈距(0.2 cm/s)、圍巖條件(0.19 cm/s)，此時埋深和交叉角度為重要影響因素，凈距和圍巖條件為次要影響因素。由此可知，在既有隧道迎爆側，凈距為最主要影響因素。

圖4 振速極差與影響因素曲線

同時結合立體交叉處既有線監測斷面兩側邊墻和拱腳的振速極差進行分析，繪制振速極差與監測點位曲線，如圖5所示。可以得到：既有線監測點距離爆源愈遠，凈距影響因素下各測點的振速極差越小。結合圖4的分析結果可得：隨著距離的增大，凈距這一影響因子對既有隧道爆破振速的影響將顯著減小。

圖5 振速極差與監測點位曲線

在既有隧道無損傷時，工程中往往僅關注迎爆側振速的大小，因此針對立體交叉段既有線監測斷面仰拱的振速極差計算過程進行分析(表6)。根據正交試驗計算原理，在進行振速極差計算時，ki值越大，說明該因素下該水平對于試驗結果的影響程度越大。

由表6可知，對于迎爆側振速而言，凈距越大，影響程度越小。交叉角度由0°變化到30°時，影響程度逐漸減小；由30°變化到60°時，影響程度逐漸增大；由60°變化到90°時，影響程度又逐漸減小。即隨著角度的變化，影響程度呈現先減小再增大再減小的變化規律；圍巖條件越差，影響程度越大；埋深的影響不是很顯著。

4 結論

(1)在立體交叉隧道接近段，根據既有線隧道各部位的爆破振速情況下，在凈距、交叉角度、圍巖條件以及埋深4種影響因素中，凈距為最主要影響因素，其他因素相較而言影響較小，而隨著測點距爆源距離的增大，凈距對各測點爆破振速的影響將顯著減小。

(2)根據既有隧道迎爆側振速，隧道凈距越大，影響程度越小；隨著交叉角度由0°變化至90°，影響程度先減小再增大再減小；圍巖條件越差，影響程度越大；埋深的影響相對不顯著。

(3)立體交叉段的既有線隧道仰拱處爆破振速，相較于其他部位測點數值較大，因此，在新建隧道施工過程中應重點監測，在既有線襯砌加固時可優先考慮；而拱頂的爆破振速測點數值最小，即受本文所述4種因素的影響有限，相比于其他部位更為安全。