黃土隧道邊坡穩定性研究

劉謙彬， 張志強

(西南交通大學交通隧道工程教育部重點實驗室，四川成都 610031)

黃土地層中隧道洞口會擾動隧道邊坡，因此研究隧道開挖后邊坡的位移、應力變化對邊坡穩定性研究具有重大災害預防意義[1]，也對邊坡加固有著指導性作用[2-4]。

謝定義[5]對黃土結構性和定量化評定進行了分析。通過對工程土進行試驗研究，揭示黃土顆粒聯結的結構特性，為黃土隧道的支護設計提供相關理論基礎。劉偉等[6]對黃土工程特性進行了分析研究。柴華友等[7]通過試驗研究，得出黃土在不排水時受到荷載作用易發生結構軟化，產生液化現象。張培文等[8]研究了彈模和泊松比對邊坡穩定安全系數的影響，給出了折減方法。邵珠山等[9]通過數值模擬分析了坡角、降水條件對邊坡穩定性影響規律。王軍等[10]利用有限差分軟件和優化的流變模型對邊坡聯合穩定性進行了研究。

隧道開挖時及隧道開挖后邊坡的位移、塑性區分布特點還不夠清晰。本文將基于以上研究，以黃土隧道為例，研究隧道洞口施工過程中邊坡的穩定性。

1 工程概況

某黃土隧道預穿越山體為黃土塬邊緣的黃土梁，其山頂標高為1 370.0 m，山底標高1 160.0 m，最大高差210.0 m。在山體北坡坡角及南坡坡角以及隧道入口附近均有黃土沖溝發育，總體由東北向西南方向發展。隧道入口坡體高30.0 m，坡角約35°，坡體成階梯狀，為人工開挖梯田，寬度6.0～10.0 m，高度4.0～8.0 m。隧道出口坡體高10.0 m，坡角約25°。圖1、圖2為隧道出、入口坡體形態。

圖2 隧道出口

2 基于極限平衡法的邊坡穩定安全系數計算

2.1 模型建立及參數選取

本文利用Geo-Slope軟件中的Slope/W計算模塊，基于極限平衡法計算邊坡的穩定安全系數并確定滑動面。

根據現場實驗資料和勘察報告，結合黃土室內物理試驗測試結果，有限元計算的參數取值見表1。

表1 計算參數取值

有限元計算模型見圖3，按平面應變問題考慮，對自然狀態下黃土邊坡的穩定性進行計算分析，其中上層為Q3粉質黏土，下層為Q2粉質黏土。

圖3 某黃土隧道入口邊坡計算分析模型

2.2 計算結果及分析

過去很少考慮含垂直節理的黃土邊坡的數值計算，本文運用Geo-Slope數值模擬軟件中的Crack單元在Q3黃土中建立垂直節理，暴雨工況是在天然工況所得到的潛在畫面基礎上，依據飽和Q2、Q3黃土室內物理力學試驗所得到的參數，并在此基礎上根據極限平衡法求得暴雨工況參數。最后將計算結果與無垂直節理工況進行對比，數值計算結果見圖4～圖7。

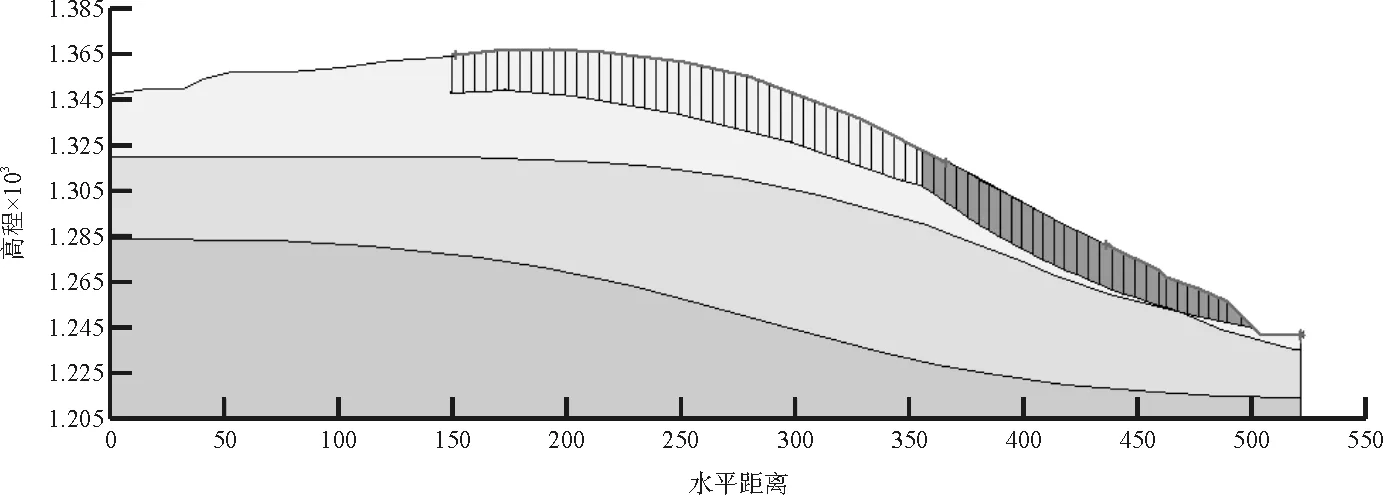
圖4 天然-垂直節理邊坡穩定性

圖5 天然-無垂直節理邊坡穩定性

圖6 暴雨-垂直節理邊坡穩定性

圖7 暴雨-無垂直節理邊坡穩定性

2.2.1 數值計算結果

(1) 隧道邊坡在天然-垂直節理下，穩定性系數為1.092，為較穩定狀態。

(2)隧道邊坡在天然-無垂直節理下，穩定性系數為1.262，為較穩定狀態。

(3)隧道邊坡在暴雨-垂直節理下，穩定性系數為0.675，邊坡失穩破壞。

(4)隧道邊坡在暴雨-無垂直節理下，穩定性系數為0.892，邊坡失穩破壞。

2.2.2 數值計算結果解讀

(1)天然工況下，隧道邊坡是否存在垂直節理對邊坡穩定性影響較小，因為隧道工程區分布的垂直節理雖分布較密集，但結合較緊密，且黃土具有很好的直立性，故天然工況下邊坡垂直節理對邊坡穩定性無較大影響。但在暴雨工況下，有無垂直節理情況下的邊坡穩定性系數差別巨大。在暴雨工況下，垂直節理為雨水的入滲提供了通道，由于Q2黃土滲透系數較小，雨水入滲以后，在Q2與Q3黃土地層分界面集聚，導致地層分界面處抗剪強度急劇降低，而垂直節理又為坡體的滑動提供了后緣拉裂面，從而導致了邊坡整體失穩破壞。

(2)自然降雨及黃土邊坡是否分布垂直節理是影響隧道口邊坡穩定性的主要因素。垂直節理降低了土體間的粘結，為邊坡的滑動破壞提供了后緣拉裂面以及為降雨的入滲提供了通道，降低了土體的粘聚力及內摩擦角，導致了邊坡的滑動破壞。

3 基于動態強度折減法的邊坡穩定安全系數計算

3.1 計算理論概述

本文提出了動態強度折減法研究邊坡從穩定狀態到局部破壞再到整體失穩的整個過程，計算過程見圖8。

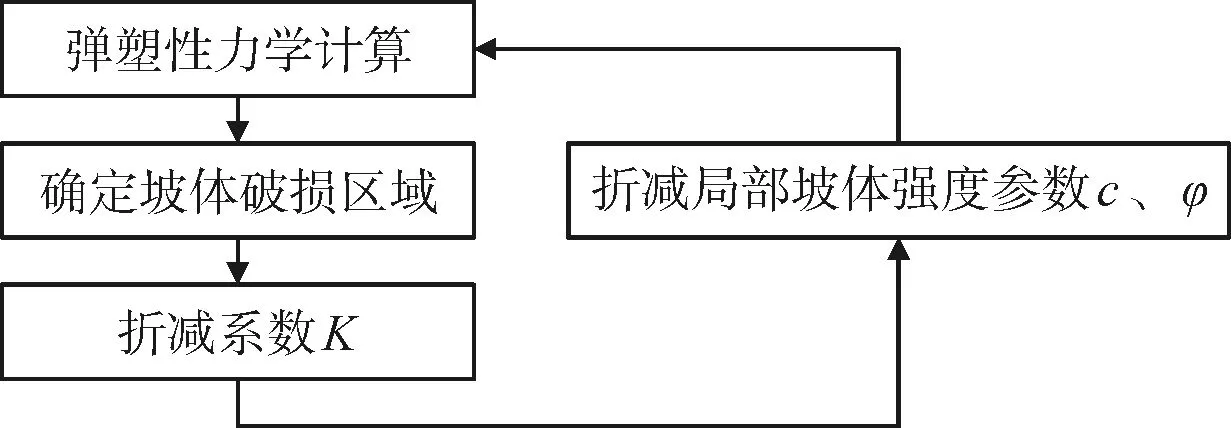
圖8 動態強度折減計算過程

本文強度準則采用Mohr-Coulomb準則，并且利用屈服接近度YAI確定動態強度折減計算過程中的屈服區域。其中YAI的取值0～1，當YAI=0時，土體發生屈服；當YAI=1時，土體處于最穩定狀態。試驗發現，巖土體在加載過程中發生屈服的應力值約為峰值強度的80%，故本文中取80%的安全閾值確定折減計算中的屈服范圍，即YAI<0.2的區域視為發生屈服。

3.2 ABAQUS建模及參數選取

根據現場試驗資料和勘察報告，并結合黃土物理力學試驗結果，有限元計算所用到的參數取值如表2所示。

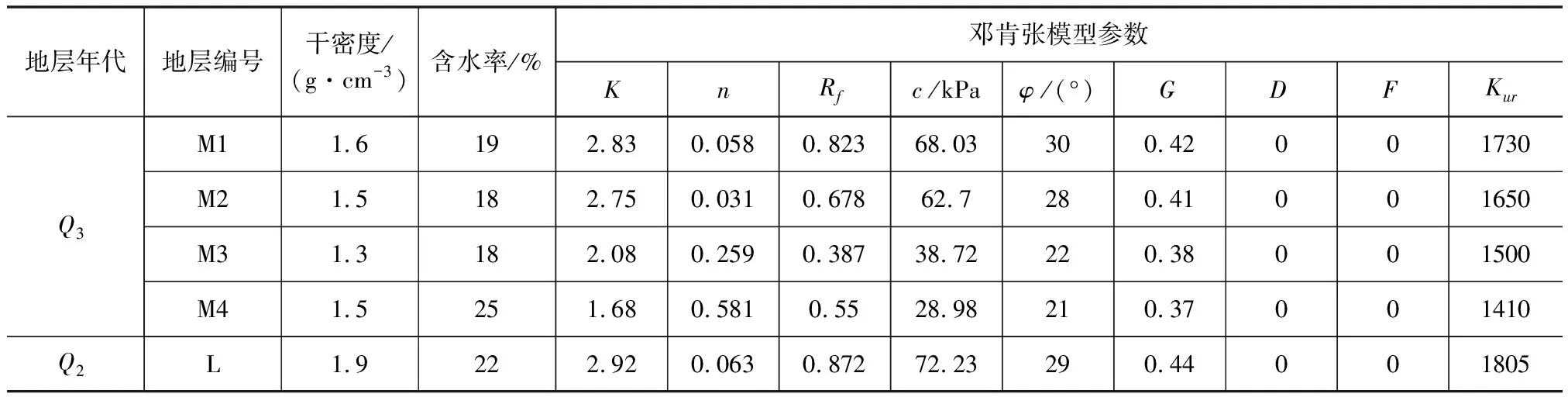
表2 有限元計算參數

計算模型網格圖見圖9，同樣按平面應變問題考慮，對自然狀態下黃土邊坡進行穩定性分析。模型共分3層，上層為Q3黃土，中層為Q2黃土，下層為基巖，模型總高和寬為140 m和370 m。

圖9 隧道進口邊坡有限元計算模型

3.3 計算結果及分析

對于天然狀態下的邊坡，僅施加重力荷載。本次分析計算設置2種工況。

3.3.1 天然工況

經過15步動態強度折減，求解后得到邊坡的等效塑性應變結果如圖10～圖12所示。

圖10 天然工況未折減塑性分布

圖11 天然工況第5步折減塑性分布

圖12 天然工況第15步折減塑性分布

從圖10～圖12可以看出，在土體強度未折減時，僅在坡頂處有小范圍的塑性區分布，土體強度未充分發揮，尚有安全儲備。隨著折減程度加大，坡腳處的塑性區逐漸擴大，坡腳塑性區應變值大于坡肩塑性區應變值，且坡腳塑性區進一步向上部及坡面發展，并逐漸貫通，最終邊坡發生破壞。當強度繼續折減時，計算不再收斂。

通過圖13可以看出，以數值計算不收斂評價邊坡穩定性，對應的FV1為1.13，即安全系數Fs=1.13，以位移的拐點評價，則Fs=1.11。

圖13 天然工況U1隨FV1(場變量)的變化關系

3.3.2 暴雨工況

經過21步動態強度折減，求解后得到邊坡的等效塑性應變變化過程如圖14～圖16所示。

圖15 暴雨工況第10步折減塑性分布

圖16 暴雨工況第21步折減塑性分布

從圖中可以看出，在土體強度未折減時，暴雨工況下由于水的作用，土的抗剪強度較天然工況下有一定程度的降低，此時土體也仍有一定強度的安全儲備，僅在坡腳及坡頂有小范圍的塑性分布。隨著折減程度增加，坡腳處塑性區進一步擴大，塑性應大于坡肩塑性應變，且坡腳塑性區不斷向上部及坡面發展并逐漸貫通，邊坡發生破壞。

強度折減至第21步時，坡肩和坡面處塑性區域趨于穩定，坡腳處塑性應變急劇增大，塑性區貫通坡面。當強度繼續折減時計算不收斂。

通過圖17可以看出，若以數值計算不收斂評價邊坡穩定性，安全系數取為Fs=0.88，以位移拐點評價，安全系數Fs=0.83。

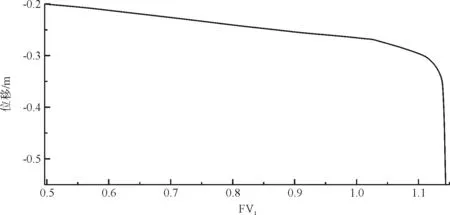
圖17 暴雨工況U1隨FV1(場變量)的變化關系

4 結論

本文基于極限平衡法和動態強度折減法，通過有限元軟件對邊坡安全系數進行了計算研究得到幾點結論：

(1)自然狀態下，邊坡是否存在垂直節理對邊坡穩定性影響較小。但暴雨狀態下，垂直節理對邊坡穩定性影響巨大。

(2)黃土邊坡的垂直節理和天然降雨是影響隧道邊坡穩定性的主要因素。垂直節理降低了土體間的連接效果，雨水入滲也會降低土體的粘聚力及內摩擦角，易導致邊坡破壞。

(3)土體強度未折減時，邊坡塑性區主要分布于坡腳和坡頂部，隨著土體強度不斷折減，坡腳處塑性區逐漸向上部坡面發展，并逐漸貫通，形成邊坡破壞。