基于四元組度量損失的多模態變分自編碼模型

陳亞瑞，楊劍寧，吳世偉，劉 垚，王曉捷

(天津科技大學人工智能學院，天津 300457)

多模態數據處理廣泛存在于自然科學、工程技術等領域，不同模態的數據往往是對同一事物不同形式的表示，又各自具有獨特的性質[1-3].在醫療健康研究領域，智能手術室中的多模態數據包括場景 RGB圖像、深度圖像、紅外圖像、音頻等，不同模態數據包含的信息既相互冗余又相互補充[1].在機器人等智能設備工程技術領域中，設備的深度攝像頭會同時采集深度圖像與 RGB圖像，當受光線等外部因素影響某模態圖像成像質量時，可利用另外的模態圖像進行輔助去噪[1-4].

采用概率生成模型處理多模態數據是一個重要的研究領域，早期基于能量的玻爾茲曼機與自編碼器模型在處理多模態數據中已經取得了較好的效果.隨著傳感器技術的發展，人類對數據的獲取無論從粒度上還是量級上都有了很大的飛躍，獲取的數據本身往往具有高維度、海量性等特點，給多模態數據研究帶來了更大的難度與挑戰.早期的模型不能有效地處理大規模數據場景下的模型訓練與推理問題，而變分自編碼(variational auto-encoder，VAE)[5-6]的提出很好地解決了該問題.研究基于 VAE框架通過建模數據的條件生成過程，實現模態之間的數據交叉與轉換生成，但這些工作未從生成角度進行多模態數據建模，限制了模型的表示能力[7-11].對多模態聯合數據分布的建模包括聯合多模態變分自編碼器(joint multimodal variational auto-encoder，JMVAE)模型[12]、多模態變分自編碼器(multimodal variational autoencoder，MVAE)模型[13]和專家混合多模態變分自編碼器(mixture-of-experts multimodal variational autoencoder，MMVAE)模型[14]等.這些模型通過建模多模態數據聯合概率分布實現多模態數據的表示、條件生成，比分別建模不同方向上條件概率分布的訓練開銷更低，數據表示更有效.但是，這些模型沒有對數據進行解耦表示.文獻[15]提出了解耦的多模態變分自編碼器(disentangling multimodal variational autoencoder，DMVAE)模型，該模型通過將模態共享信息與私有信息分開表示，并最小化隱向量的互信息進行解耦表示，通過噪聲對抗估計損失在隱空間對齊共享隱向量，效果較好，但該模型仍然存在數據生成質量不清晰與共享私有信息抽取不準確的問題.

已有的研究工作對不同模態數據之間的共享信息沒有顯式的約束，這使多模態數據的共享信息與私有信息不能被高效地解耦表示，進而導致信息抽取不準確、生成數據模糊.本文提出基于四元組度量損失的多模態變分自編碼(quadruplet metric loss based multimodal variational auto-encoder，Q-MVAE)模型，在分開建模共享信息與私有信息的基礎上，建模不同模態的聯合概率分布與單模態邊緣概率分布，并且引入了四元組度量損失約束共享隱向量在隱空間對齊，使模型獲取更好的數據生成與表示能力.模型可以分別有效推理多模態數據的共享表示和私有表示，這些表示不僅能夠進行準確的、高質量的多模態數據交叉生成與轉換生成，而且能夠用于多模態數據分類等下游任務.相關的定性與定量實驗證實了本文模型擁有更好的數據表示能力與生成能力，同時表明模型對私有信息生成因子展現了一定程度的解耦表示能力.

1 相關工作

1.1 多模態概率生成模型

早期基于能量的玻爾茲曼機與自動編碼器模型的生成模型[8-10]在視頻、音頻等多模態數據下的語音識別任務中取得了較好的識別準確率.這些模型往往采用馬爾可夫鏈蒙特卡羅方法訓練模型，難以處理高維大數據的場景.研究人員[5-6]提出了 VAE框架，通過引入變分推理與重參數化技巧，使生成模型可以在大數據場景下進行有效訓練.這使以 VAE為框架的多模態概率生成模型成了多模態數據處理領域的重要研究方向.Kingma等[7]和 Sohn等[8]在 VAE框架的基礎上提出了條件變分自編碼器(conditional variational auto-encoder，CVAE)，通過最大化條件似然，可以基于標簽等信息進行有條件的數據生成.基于 CVAE的改進模型[9-10]可以學習模態間的條件關系，但是條件關系是單方向的，模型的推理表示能力有限.Wang等[11]提出了雙向變分典型相關性分析模型 (bidirectional variational canonical，correlation analysis，BiVCCA)，基于典型相關性分析思想，設計學習兩模態數據私有信息的編碼器，實現了數據交叉生成，但是其條件關系也是單向的，模型訓練開銷較大，難以擴展到兩模態以上場景.

Suzuki等[12]提出了JMVAE模型，該模型直接建模多模態數據的聯合分布，這使其比建模條件分布的模型具有更低的訓練開銷，也可以有效地從聯合分布中推導條件分布，然而該模型也存在計算開銷會隨著模態數目的擴展呈指數級增長的問題.Wu等[13]提出了MVAE模型，Shi等[14]提出了MMVAE模型，這些模型都直接建模多模態數據的聯合分布，并利用邊緣后驗分布擬合聯合后驗分布.其中，MVAE模型通過引入專家積函數[16](product of experts，PoE)對邊緣后驗分布進行幾何平均運算，MMVAE通過引入專家和函數(mixture of experts，MoE)對邊緣后驗分布進行算術平均運算，都較好地解決了多模態下的計算開銷問題，也一定程度解決了缺失模態下的推理表示問題.Sutter等[17]提出了專家混合積函數變分自編碼(mixture，of products of experts variational autoencoder，MoPoE-VAE)模型，該模型提出了一個更泛化的多模態生成模型的下界，整合了 MVAE與MMVAE模型的特點，并在其理論框架內將這兩個模型視為其模型的特殊情況.但是，上述工作都未考慮多模態數據共享信息與私有信息的解耦表示.Daunhawer等[15]提出了DMVAE模型，該模型對每個模態的共享信息與私有信息都進行了解耦表示，并引入噪聲對抗估計損失在隱空間對齊共享隱向量，有效地提高了模型的數據表示能力與生成能力，但該模型沒有顯式地約束共享隱向量，導致該模型存在信息抽取不準確以及生成的數據質量模糊的問題.

1.2 度量學習

利用樣本之間的相對距離關系學習數據表示的度量學習與對比學習在模式識別、表示學習領域取得了出色的效果[18-21].Schroff等[18]提出了三元組損失并應用于人臉識別中，其作為一種度量學習方法通過約束樣本標簽，使相同的人臉圖像在編碼空間的距離小于不同樣本標簽來學習人臉的向量表示.Chen等[22]提出了四元組損失并將其應用于行人重識別任務中，四元組損失能夠約束模型在特征空間更好地識別不同攝像頭視角下的行人.Ishfaq等[23]將三元組損失引入 VAE模型，利用不同標簽的三元組正負樣本進行對比訓練，數據表示效果較好，同時在隱空間編碼了更多的相似語義結構信息.Shi等[24]提出利用樣本之間的相關性關系進行對比學習，有效提升了MVAE、MMVAE等多模態生成模型的訓練效率.

本文受到上述工作的啟發，在將共享信息、私有信息分開推理表示的基礎上，將四元組度量損失引入概率生成模型中，以顯式約束模型編碼網絡學習到不同模態的共享信息，在模型訓練時同時考慮數據完整與模態數據缺失的情況，以使模型具備在模態數據缺失情況下的推理表示能力與生成能力.

2 背景知識

本文模型基于 VAE[5-6]概率生成模型框架，該框架使模型可以在高維大規模數據場景下，使用隨機梯度下降方法進行有效訓練.

VAE框架假設給定觀測數據x，以及對應的隱變量 z，其 生 成 過 程 為 x ～ pθ(x|z )，其 中 z ～ p(z)=N ( 0,I)，θ是生成器網絡p的參數.VAE的目標是最大化式(1).

但是，式(1)是不可計算的，VAE轉而計算其證據下界(evidence lower bound，ELBO)，即

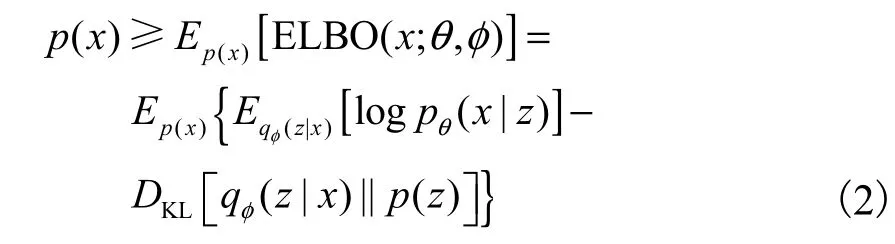
式 中 ： Eqφ(z|x)[l o g pθ(x|z)]為 負 重 構 誤 差 ，DKL[[qφ(z|x) ||p(z) ]]為正則化項；pθ(x|z)為生成器網絡，參數為 θ；qφ(z|x)為編碼器網絡，參數為φ.VAE的目標是利用參數 θ和φ最大化式(2).為了使其能夠在神經網絡上進行訓練，提出了對隱變量z進行重參數化，即假設qφ(z|x)為高斯分布 N (z;μ, d iag(σ2) )，φ={μ,σ2} ，將 z ～ qφ(z|x)重參數化為z =μ+σ⊙ε，其中ε～ N(0,I).以 VAE為框架的模型訓練完成后，就可以得到 1個編碼網絡和 1個生成網絡.編碼網絡對數據進行表示推理，生成網絡隨機生成、重構數據[5, 25-26].

3 本文模型

3.1 模型架構

針對多模態數據的表示與生成問題，本文提出Q-MVAE模型，模型假設多模態數據生成過程由共享隱向量與私有隱向量共同決定，該假設已經在最新的一些研究工作中展現了其優越性[15].Q-MVAE模型通過共享隱向量與私有隱向量的組合生成特定模態數據，在推理過程中，模型也分別推理每個模態數據的共享隱向量與私有隱向量.對于多模態數據共享信息抽取與訓練，本文提出了四元組度量損失，用于在隱空間對齊共享隱向量，顯式地約束編碼網絡學習不同模態數據的共享信息，模型架構如圖1所示.

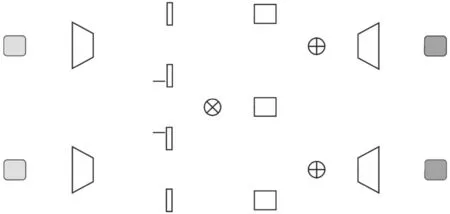
圖1 Q-MVAE模型架構圖Fig.1 Architecture of Q-MVAE model

3.2 模型生成與推理過程

Q-MVAE模型可以處理兩模態及以上模態數量的多模態數據，本文以兩模態數據(x,y)為例進行推導，假設不同模態數據樣本包含相同的共享信息與不同的私有信息，令生成數據(x,y)的共享隱向量為 z，私有隱向量分別為hx與hy.模型對數據的聯合概率分布建模為

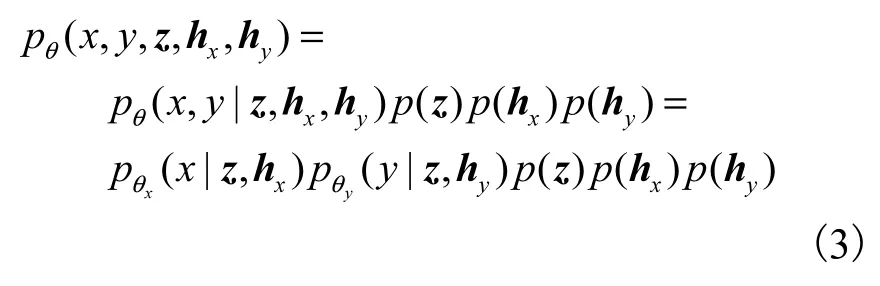
其中：p ( z) 、 p ( hx)、 p (hy)分別為隱向量 z、hx與hy的先驗分布，均服從各向同性的高斯分布；pθx( x |z,hx)和 pθy( y|z,hy)分別為 x和 y的生成器，參數為θ=｛θx,θy｝.對于兩模態數據集，模型的目標是最大化數據聯合概率分布與邊緣概率分布的對數似然函數，以得到模型參數.

為了符號表示簡便，下文以單觀測樣本的多模態數據對(x,y)為例進行推導，單觀測數據對的邊緣概率分布為

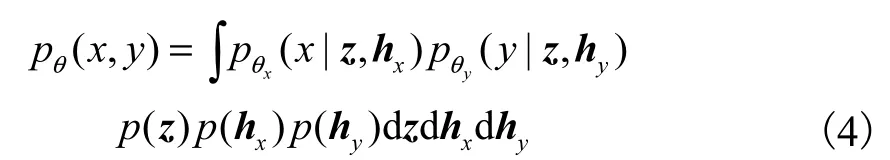
但是，式(4)中的積分是難解的，本文采用變分推理的方法進行近似求解，引入變分分布 q ( z,hx,hy|x,y)作為真實后驗分布的近似，對似然函數進行變換

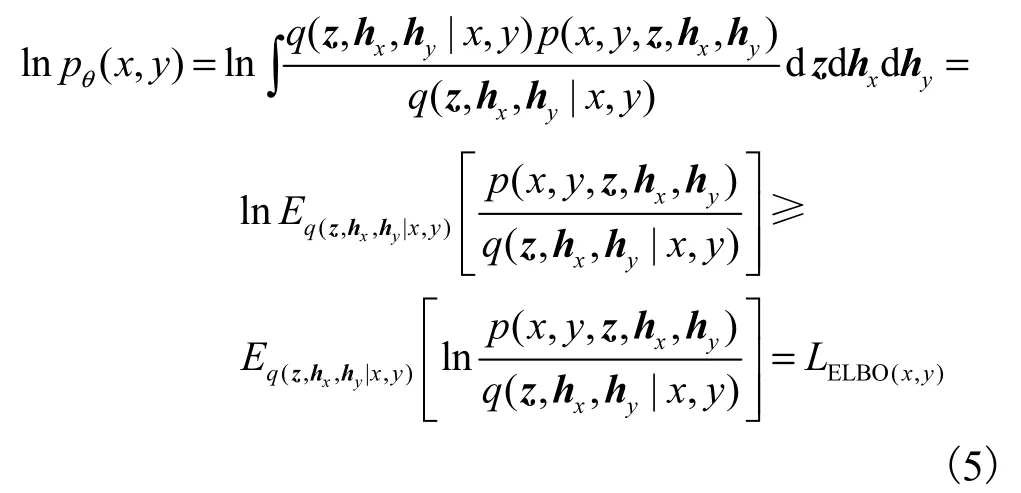
對變分分布進行分解

其中：qφhx(hx|x)與 qφhy(hy|y)為Q-MVAE模型的私有信息編碼器，參數分別為

將式(3)與式(6)代入式(5)中，可得到lnpθ(x,y)的變分下界

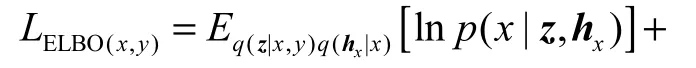
其中：q(z|x,y)是x和y的共享隱向量近似后驗概率分布.當x和y同時存在時，模型在訓練時采用專家積函數(PoE)[13,16]的方法將不同模態的邊緣后驗分別整合為聯合后驗

其中：p(z)為先驗分布，服從標準高斯分布；qφzx(z | x)與(z | y)為 Q-MVAE模型的共享信息編碼器，參數分別為、，服從各向同性的高斯分布.

模型同時、同步針對數據缺失情況下進行訓練，以使模型擁有數據缺失情況下的數據推理與生成能力.式(9)與式(10)為模態數據缺失下的概率分布.

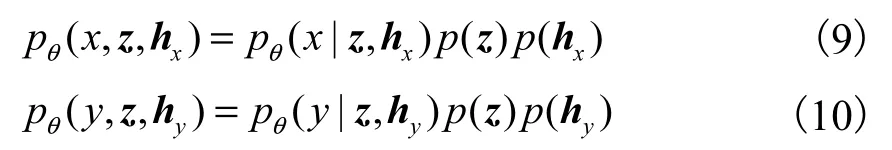
對應的邊緣概率分布分別為

相應地引入變分分布 q (z,hx|x)與 q (z,hy|y)，對式(11)與式(12)進行變換

對變分分布進行分解

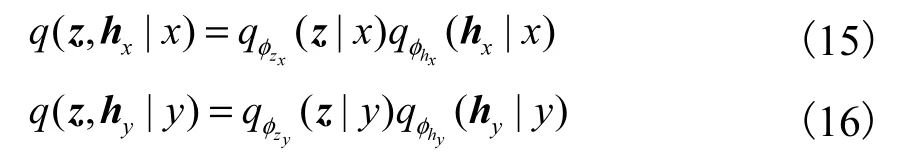
將式(15)與式(16)分別代入式(13)與式(14)中，可分別得到lnpθ( x)、lnpθ(y)的變分下界

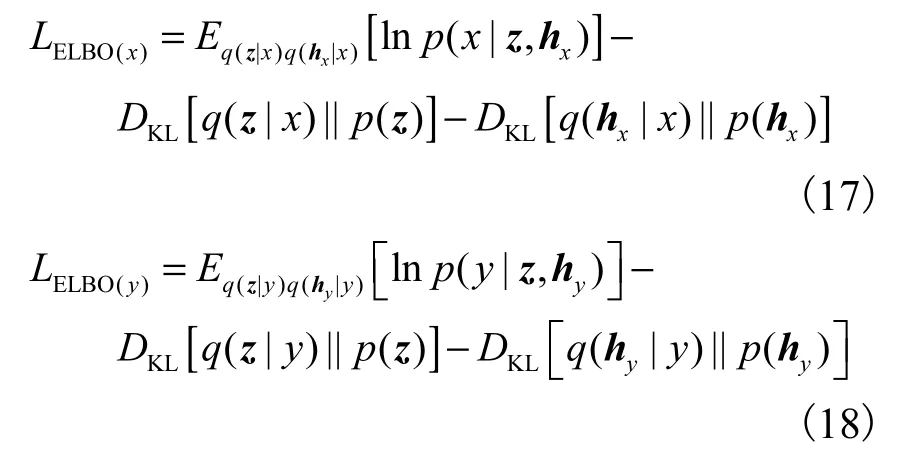
3.3 四元組度量損失

在 VAE框架下，直接最大化式(8)、式(17)、式(18)即可進行模型訓練，由于本文提出的 Q-MVAE模型對每個模態數據的共享信息與私有信息進行分開推理表示，因此不同模態的共享隱向量需要在隱空間進行對齊.基于該問題，本文引入四元組度量損失，通過顯式地約束不同模態數據樣本在隱空間的度量對比關系，使蘊含相同共享信息特征的隱向量之間的度量盡可能小，使蘊含不同共享信息特征的隱向量之間的度量盡可能大.四元組的定義為(x,y,x-, y-)，其中x和y表示描述同一對象的兩種模態數據樣本，蘊含相同的共享信息，x-和y-表示對應的負樣本，與對應的正樣本x和y蘊含不同的共享信息.以圖2為例，圖中為兩種模態的數字圖像，分別是 MNIST[27]手寫數字圖像與 SVHN[28]街景門牌號數字圖像，定義數字類別特征為共享信息，一個四元組可由圖中的樣本組成，x和 y分別為數字類別為“2”的 MNIST與 SVHN 圖像，x-為數字類別為“5”的 MNIST圖像，y-為數字類別為“8”的 SVHN 圖像，x-和y-也可以是“2”以外的任何數字類別的圖像，x-與y-的數字類別關系沒有要求，可相同也可不同.

圖2 四元組樣本示例Fig.2 Samples of quadruplet

四元組度量損失的約束目標為

其中μx(x)與μy( y )分別表示取 qφzx(z | x)與 qφzy(z |y )輸出結果均值 μ的部分.式(19)右側的第一項與第二項分別約束正樣本對 x和 y之間的度量小于正樣本與負樣本x-和y-之間的度量，α1為對應超參數；第三項約束正樣本對 x和 y之間的度量小于任意兩個不同模態數據負樣本之間的度量，α2為對應超參數.

3.4 模型最終的目標函數與訓練

聯合式(8)、式(17)—式(19)可以得到 Q-MVAE模型最終的目標函數為

其中β為超參數.模型同時考慮模態數據完整與部分缺失情況下的訓練.在模態數據完整情況下，模型對不同模態數據的共享隱變量 z通過PoE進行積函數混合，由于編碼網絡均為高斯分布，所以混合后仍為高斯分布，其均值與方差的計算具有解析解[13,16]，可直接用于模型訓練.在模態數據缺失情況下，模型直接使用編碼網絡 qφzx(z | x)與 qφzy(z | y)的輸出結果 z作為共享隱變量 z.對于 Lquad(x,y,x-, y-)部分的訓練，需要為正樣本對 x和 y選擇相應的負樣本x-和y-.本文先從數據集中隨機選取樣本作為負樣本，然后利用訓練中的模型篩選負樣本進行模型訓練，最后將模型最終的目標函數整體取負，就可以使用梯度下降方法進行模型訓練與優化.

4 實 驗

4.1 數據集與實驗設置

實驗采用多模態數據集 MNIST-SVHN[14]評估Q-MVAE模型的性能.數據集包含 MNIST[27]手寫數字圖像(分辨率為 1×28×28)、SVHN[28]街道門牌號數字圖像(分辨率為 3×32×32)兩種模態的數字圖像，文獻[14]將上述兩種模態的每張數字圖像與另一種模態相同數字類別的20張圖像分別組成擁有相同數字類別的圖像對，形成了 MNIST-SVHN數據集，包括1682040對訓練樣本，300000對測試樣本.

在該數據集下，實驗訓練迭代次數為 10，批大小為 128，隱空間維度為 20，訓練中的超參數取值為{α1,α2,β} = { 2 ,0.8,1500}，使用 Adam[29]進行訓練優化，學習率為 0.0001.對于 MNIST模態圖像數據采用全連接神經網絡，對于 SVHN模態圖像數據采用卷積神經網絡，其中卷積核大小為 3×3，卷積步長為2，填充值為 1.

4.2 數據生成

數據交叉生成與轉換生成是多模態生成模型的核心能力.由于 Q-MVAE模型將數據的共享信息與私有信息分開推理表示，通過已知的條件模態數據樣本輸入相應的共享信息編碼網絡，得到樣本的共享隱向量，將其與從目標模態數據的私有隱向量先驗分布中采樣結合，再輸入目標模態數據解碼網絡，完成數據交叉生成.數據轉換生成與交叉生成類似，不同之處在于通過將已知的參考樣本輸入相應私有信息編碼網絡，得到私有隱向量，將其與之前獲得的共享隱向量結合輸入目標模態數據解碼網絡，完成數據轉換生成.

4.2.1 數據交叉生成

數據交叉生成實驗包括定性與定量實驗，分別對比 MVAE[13]、MMVAE[14]、DMVAE[15]模型，其中DMVAE模型為目前MNIST-SVHN數據集[14]的數據交叉生成與轉換生成效果最好的模型之一.定性實驗驗證對比各模型的數據生成質量與多樣性(圖3)，定量實驗驗證對比各模型數據交叉生成的準確性(表1).定量評估方法以測試集所有數據為條件樣本分別做MNIST到SVHN以及反方向的數據交叉生成，然后將交叉生成的圖像送入對應模態數據的圖像分類器中進行分類，計算分類結果與條件樣本標簽匹配的準確率.其中，圖像分類器指預先訓練好的MNIST與 SVHN圖像分類器.為了確保公平性，本文實驗采用文獻[14]公開的圖像分類器.

圖3 交叉生成實驗效果Fig.3 Cross generative results

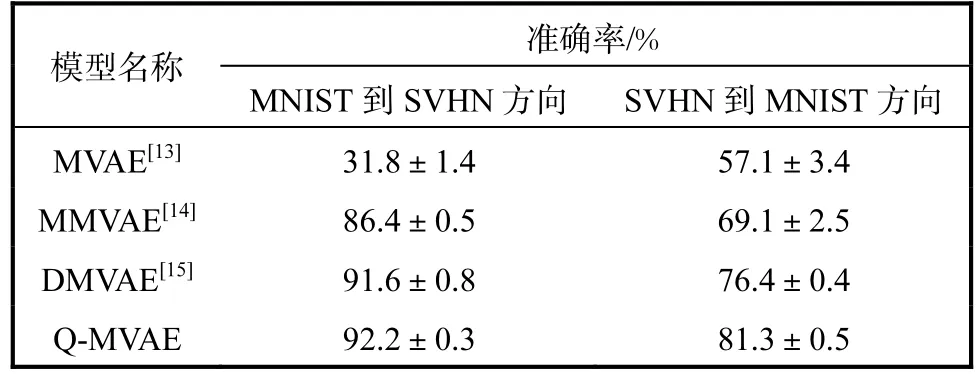
表1 數據交叉生成準確率實驗結果Tab.1 Experiment results of data cross generative accuracy

圖3的生成效果圖中，每張第1行為已知的條件模態樣本，其余行表示生成的缺失模態樣本，具有隨機的私有信息，每一行的共享隱向量從對應條件模態樣本中抽取且與私有隱向量相同.圖3(a)—圖3(d)為從條件 SVHN模態數據生成 MNIST模態數據的生成結果，結果表明：本文的Q-MVAE模型可以生成具有隨機風格，且與已知樣本相同數字類別的清晰圖像.其中圖3(a)中第 1行生成數據具備較粗字體的風格，第 4行生成數據具備較為纖細字體的風格，第7行與第10行生成數據分別具備字體前傾和后傾角度的風格，并且每張生成圖像與對應條件樣本的數字條件均相同.各對比模型中，DMVAE模型也可以較為準確地生成具備隨機風格的圖像，如字體粗細與字體角度，但是其生成的圖像中部分圖像數字難以辨認類別，如圖3(b)的第 3列與第 9列的部分生成圖像.MMVAE模型和 MVAE模型的生成圖像中僅有部分與條件樣本數字類別相同，生成的圖像也較為模糊，甚至不完整.圖3(e)—圖3(h)表示從條件MNIST模態數據生成SVHN模態數據的實驗效果，結果表明：本文的 Q-MVAE模型可以生成統一字體與背景風格的圖像.圖3(e)中的第 3行與第 6行的圖像背景左側嵌入了白色的粘連陰影，第8行的數字圖像有藍色和白色的背景.這些較為復雜的背景正是SVHN數據集的圖像風格特征，DMVAE模型也可以將相應的風格特征嵌入生成圖像中，MMVAE模型與 MVAE模型不僅生成的數字模糊，而且沒有很好地抽取生成SVHN的風格特征.

表1展示了 Q-MVAE的數據交叉生成準確率，實驗均在不同隨機種子下進行了 5次獨立實驗.由表1可知：本文模型在兩模態不同方向上的交叉生成準確率均超過了其他模型，其中從 SVHN到 MNIST方向的交叉生成準確率比目前效果最好的 DMVAE模型提升了 4.9%，這與圖3的定性生成效果相吻合.根據已知的條件樣本，Q-MVAE可以很好地抽取其共享信息，并且能夠準確地生成擁有該共享信息的其他模態數據.

4.2.2 數據轉換生成

數據轉換生成實驗為定性實驗，對比模型為DMVAE模型[15]，轉換生成實驗效果如圖4所示.圖4中每張效果圖的第一行為已知的條件樣本，提供共享信息(本實驗為數字類別信息)，第一列為已知的參考樣本，提供私有信息(本實驗為字體與背景等風格信息).從圖4中可以看出，Q-MVAE模型可以準確抽取圖像的公有與私有信息，并且可以進行相應的轉換生成，生成質量更為清晰.

圖4 轉換生成實驗效果Fig.4 Translation generative experimental results

圖4(a)為MNIST到SVHN方向的轉換生成，生成的圖像均準確地從條件樣本中抽取了數字類別信息，同時準確地抽取了參考樣本的字體風格與顏色背景信息.值得注意的是：圖4(a)第3行參考樣本中數字右側背景有粘連的白色背景特征被模型準確地抽取到且成功嵌入生成圖像；第4行參考樣本原始圖像比較模糊，模型將該圖像的模糊當作了私有信息進行抽取并成功生成了相似風格的圖像.DMVAE模型也基本可以進行準確的共享私有信息抽取與生成，但是圖4(b)第 3行生成效果中并沒有準確抽取參考樣本的私有信息，而生成的是具有不同風格的特征且較為模糊的圖像.圖4(c)為 SVHN到 MNIST方向的轉換生成.圖4(c)第 2行與第 4行成功抽取到參考樣本的相對粗壯字體風格信息，第3行、第7行與第10行成功抽取到參考樣本的數字角度信息，并且都嵌入生成圖像中，整體生成質量清晰準確.圖4(d)的DMVAE模型生成質量較為模糊，第8列生成圖像沒有準確抽取共享信息，其將條件樣本的數字類別“6”錯誤地轉換生成為數字類別“9”.

4.3 多模態數據分類

概率生成模型對數據的表示隱向量可被用于數據分類等下游任務[2].為了驗證 Q-MVAE模型在下游任務中的性能，在 MNIST-SVHN多模態數據集上進行了對比實驗，比較模型的多模態數據分類能力.將訓練集所有樣本輸入模型的共享信息編碼網絡，經過專家積函數混合之后得到共享隱向量，與訓練集樣本對應的數字標簽訓練一個線性分類器，然后將測試集所有樣本分別輸入共享信息編碼網絡，得到測試集數據樣本的共享隱向量，使用上述訓練好的單個線性分類器可以同時對不同模態數據進行分類.多模態數據分類準確率實驗結果見表2.線性分類器是一個單層神經網絡，其參數與文獻[14]的公開代碼一致，輸入維度為20，輸出維度為10.

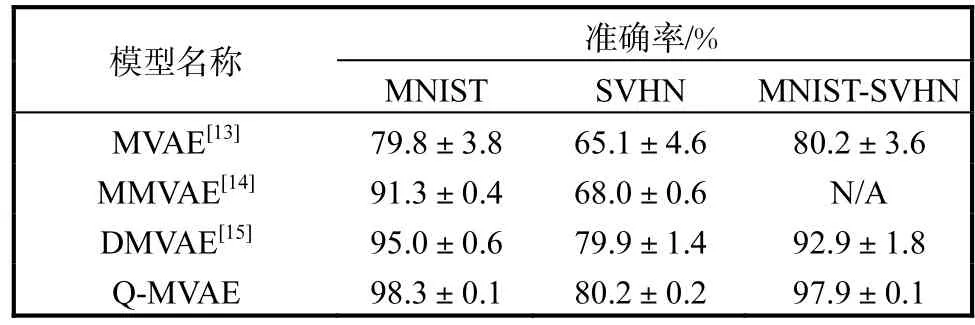
表2 多模態數據分類準確率Tab.2 Experiments of multimodal data classification accuracy

從表2可以看出，Q-MVAE模型的分類準確率均高于各對比模型.Q-MVAE模型僅通過單模態數據就可以進行高準確率分類，在兩模態數據同時提供的情況下，模型分類準確率較僅提供 SVHN模態數據有明顯提升，但略低于僅提供 MNIST模態數據.這表明模型從兩個模態數據中抽取了比單模態數據更多用于分類的信息.同時，MNIST模態數據的共享信息特征相較于 SVHN模態數據更易被抽取，從兩個模態抽取的共享信息進行融合之后，可以較大程度提高 SVHN的分類準確率，但是從 SVHN數據中抽取的誤差信息也會微弱地影響從MNIST數據中抽取相對準確的信息.因此，Q-MVAE模型可以很好地抽取表示不同模態數據的共享信息，使用單個線性分類器同時對不同模態數據分類均取得高的準確率，也表明本文提出的四元組度量損失對不同模態的共享隱向量在隱空間進行了很好的對齊.

4.4 解耦表示生成

通過設計對私有信息的解耦表示與生成實驗，驗證模型對私有信息的抽取與表示性能.基于 MNISTSVHN數據集下的交叉生成實驗，設計將私有隱向量除某維度之外的所有維度值不變的前提下，對該維度的值進行線性微量變化，觀察圖像生成效果.圖5為在兩個方向上的交叉生成，其中對私有隱向量中的10個維度進行逐維度線性微調數據生成.

圖5 有解耦特性的交叉生成實驗效果Fig.5 Experiments of cross generative with decoupling feature

以圖5(a)中的第 1行生成圖像為例，該行圖像為固定私有隱向量除第1維度以外所有維度的值，并將第 1維度的值在－5～5之間等間距取 20個值分別生成第 1行的20張圖像，即生成每一行圖像的私有隱向量只有第1維度的值有微小差別，以下各行為依次改變其他單一維度的值生成的圖像，以此觀察對隱向量生成因子的解耦表示與生成.從圖5(a)中可以看出：第1行生成的數字大小隨著私有隱向量第1維度值的微量增大而變大，可以認為私有隱向量第 1維度解耦地學習到字體大小的生成因子；第5行的數字角度隨著私有隱向量第 5維度的改變由數字角度后傾慢慢變為數字角度前傾，可以認為第5維度學習到控制數字角度的生成因子；第 10行可以被認為學習到背景明暗的生成因子.從圖5(b)中看出：第1行對應隱向量學習到數字角度的生成因子，第3行對應隱向量學習到數字字體粗細的生成因子，以下各行則學習到字體胖瘦與不同字體風格的生成因子.

通過上述實驗可以看出，對多模態數據進行共享信息與私有信息解耦表示，并顯式地約束共享信息進行對齊，可以使模型在多模態交叉生成、轉換生成與數據分類等下游任務中取得更好的效果.此外，解耦表示生成實驗還使模型展現了對圖像風格信息等更細致生成因子推理的潛力.

5 結 語

針對多模態數據生成問題，提出了一個基于四元組度量損失的多模態變分自編碼模型 Q-MVAE.該模型在對多模態數據的共享信息與私有信息解耦表示的架構下，引入了四元組度量損失，顯式地約束模型訓練時在隱空間對共享隱向量進行對齊，有效提高了模型的數據表示與生成能力.相關對比實驗證明了 Q-MVAE模型可以有效學習、抽取與表示多模態數據的共享信息與私有信息，并能利用這些表示隱向量進行數據生成與重構，也能進行多模態數據分類等下游任務.Q-MVAE模型通過逐維度操控私有隱向量進行風格漸變的數據生成展現了對數據的解耦表示潛力.在保證模型數據生成質量與多樣性的前提下，如何更好地對多模態共享信息與私有信息生成因子進行解耦表示與生成是下一步的研究重點.