含光伏低壓配電網邊端功率-電壓控制方法

李浩，曹華珍，吳亞雄，張俊瀟，成潤婷，曾慶彬

（1.廣東電網有限責任公司電網規劃研究中心，廣州 510062；2.廣州市奔流電力科技有限公司，廣州 510640）

0 引言

新型電力系統建設和光伏政策落實以達成“雙碳”目標的背景下，可再生能源發電海量接入，進一步擴大分布式電源（distributed generation，DG）在配電網的滲透率［1-5］。隨著中小型光伏（photovoltaic，PV）并網系統快速增長，其出力不確定性以及功率倒送使低壓配電網的運行面臨巨大挑戰［6-7］。雙向、強隨機性的潮流引起節點電壓大范圍隨機波動，PV的不均勻接入也將進一步加劇三相不平衡。同時，低壓配網無法消納的大量剩余功率通過配電變壓器上送至中壓配網，造成配變嚴重過載［8］。

隨著配電物聯網“云-管-邊-端”體系架構逐漸完善，海量臺區智能終端的引入與升級可為配電網提供大量監測與用戶信息，為分布式電源管理提供可靠決策依據［9-10］。目前，在配電網優化控制研究中，基于分布式［11-13］通信架構的功率-電壓控制研究尚不充分。多數文獻通過潮流計算或靈敏度分析進行全局優化［14-16］或本地控制［17-19］，較少從系統層面同時考慮網絡拓撲依賴、臺區安全運行問題。針對低壓配電網基礎通信設備和拓撲信息欠缺、運行方式多變等特點，基于最優潮流計算的集中優化［20-21］方法由于對潮流模型參數極度依賴而難以應用，而分散優化方式無法調用多設備進行全局優化［22］。另外，已有研究對PV功率大量倒送考慮不足，無法對配變過載進行合理管控。

為此，本文提出基于配電物聯網的含光伏低壓配電網邊端功率-電壓控制方法。該方法貢獻包括：

1）基于拓撲自動識別下邊端分布式通信架構，建立高密度光伏接入下臺區功率-電壓多模態控制模型。整體架構進一步降低網絡拓撲的依賴度，通過節點電壓和功率利用率切換控制模式來提高可再生能源消納，實現臺區運行優化；

2）在上述控制模型中，文章提出了在配變負載約束下的全光伏功率控制方法，可在滿足配變安全運行下實現功率精確控制，緩解節點電壓與功率交換的多目標控制矛盾性；

3）提出該分組通信架構下受控節點的選擇原則，提供通信拓撲權值優化方法并進行穩定性分析。

1 拓撲識別下的“邊-端”分布式通信架構

在配電物聯網體系架構中，臺區智能終端與底層端設備的關聯拓撲具備自動識別功能。首先將低壓配電網PV按單相、三相劃成不同的通信系統來實現分布式優化。基于文獻［9］“邊-端”拓撲識別技術，將系統所有可鄰接通信的設備納入“端”類管理。

臺區智能終端抽象為根節點，線路分支箱及集中智能電表箱作為二級分支節，PV設備作為末端節點的樹形拓撲。構建分布式邊端控制通信架構如圖1所示。集中智能電表箱下同相PV劃為3個控制小組。無法納入集中管理的其他單相PV選擇適合的低壓分支箱配監控終端等智能設備作為通信中心，按相序構成3個控制小組；剩余少量三相光伏構成一個控制小組，再分相控制。各控制組的智能設備再與臺區智能終端進行信息交互。

眾多邊端智能設備可自動識別“臺區智能終端-分支監測終端-用戶表箱-PV設備”的電網拓撲和分布式電源通信拓撲關系，并依托配電物聯網中寬帶載波技術快速識與更新通信拓撲信息［9］，實現即插即用。以附圖A1低壓配電網拓撲為例進行控制構建示例，得“臺區智能終端-分支監測終端-用戶表箱-PV設備”通信系統如附圖A2—A3所示。

2 低壓配網邊端多模態功率-電壓控制方法

2.1 低壓配網邊端多模態功率-電壓控制模型

分布式系統中鄰接PV跟隨主導PV更新自身狀態，其離散控制率可表示為［23］：

式中：xi為第i個PV的狀態量；dij為PV通信矩陣D中的元素；k為迭代次數；N為設備數量；ε為迭代步長；σi為第i個PV的主導系數，主導PV的σi=1，否則為0；v為模態選擇信號矩陣；Δxref為主導PV狀態變化參考值矩陣。以功率利用率為一致變量，標幺值計算下目標函數f為［12］：

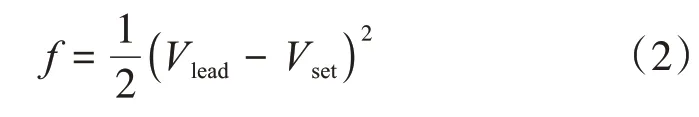
式中：Vlead為主導PV的節點電壓；Vset為參考電壓。以f對利用率x的負偏導作為變化參考值［12］，以常見低壓線纜自導納計得常系數κ替代網架參數，功率利用率變化參考值Δxpv，ref、Δxqv，ref表達為：

式中：Vi為第i個PV接入節點電壓；Ppv，i為第i個PV輸出有功功率；PPV，max，i為第i個PV最大輸出有功功率；κ為節點i的自導納；QPV，i為第i個PV輸出無功功率；QPV，max，i為第i個PV當下最大無功可調容量。系統運行約束包括電壓上下限約束、臺區首端公共連接點（point of common coupling，PCC）功率交換約束、PV出力約束為：

式中：Vmax和Vmin分別為節點電壓上下限；PPV為光伏系統有功出力；PPV，max為光伏系統最大有功出力，取決于太陽輻照度；SPV為PV的容量；PPCC，min、PPCC，max分別為PCC點有功功率交換最小值、最大值；QPCC，min、QPCC，max為PCC點無功功率交換最小值、最大值，方向均為上級網絡到低壓配電網。

2.2 低壓臺區節點電壓多模態控制

為保證PV最大消納，當臺區運行在約束內，保持不棄光，利用PV無功功率對電壓不平衡進行優化；當臺區節點電壓幅值和有功功率利用率達到模式切換需求，以PV有功功率調節電壓偏差，再通過PV剩余無功功率進行三相電壓不平衡補償。當考慮可再生能源消納、PV有功出力不削減時，其有功功率利用率變化量設為常數表示以此速率恢復到最大出力。整理得有功利用率變化量參考矩陣ΔxPV，ref為：

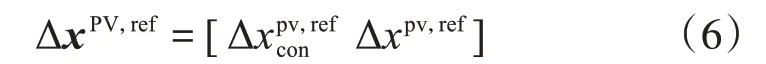
控制組均以主導PV接入節點為電壓控制的受控節點，通過式（3）更新有功功率變化量參考值，Vset=1.0。本文采用電壓不平衡IEEE標準定義［24］，具體公式為：

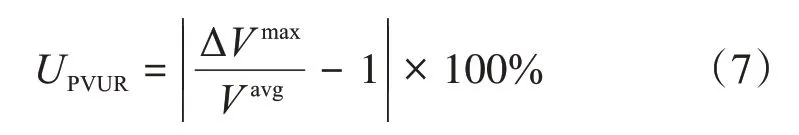
式中：Vavg為三相電壓均值；ΔVmax為三相電壓與均值Vavg最大差值的絕對值。所有控制組均通過式（4）更新無功功率利用率變化量參考值。對于集中智能電表箱控制小組，Vset=Vcenter，avg，Vcenter，avg為受控節點的三相平均電壓；對于其他單相PV構成的控制小組，Vset為低壓配電網中選定受控節點的Vavg；對于三相PV構成的控制小組，考慮三相逆變器分相補償不平衡的能力，Vset為三相PV接入節點的Vavg。

綜上，在考慮配變負載約束前，第i個PV功率利用率第k+1次迭代多模態更新模型為：

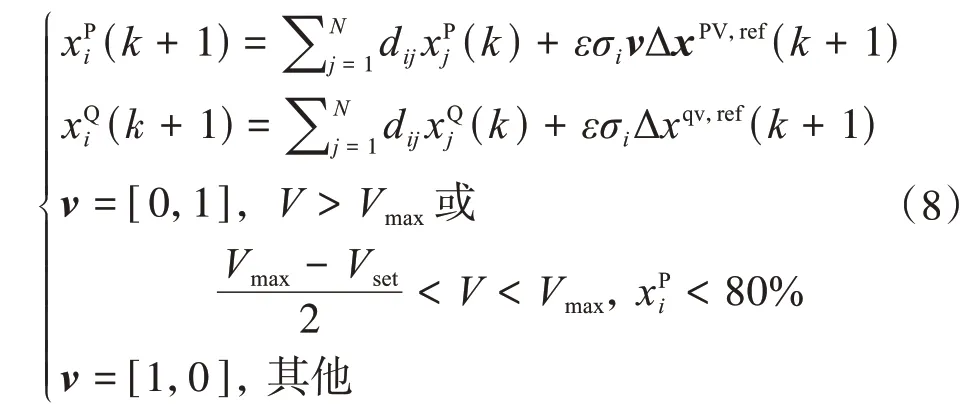
式中：為第i個光伏無功功率利用率，為第i個光伏有功功率利用率N為臺區內PV數量。第i個PV有功功率和無功功率分別為：

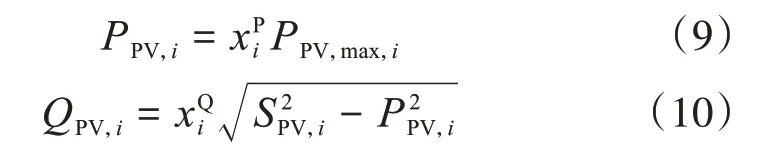
2.3 考慮配變負載的功率控制

配電變壓器負載運行存在限制，僅削減饋線首端PV出力［11］難以滿足需求，臺區單類設備亦無法兼顧多個控制目標［12］。因此，本文考慮配變負載約束，以全光伏功率控制方法來修正光伏出力，此時有功功率利用率由式（11）—（12）更新。

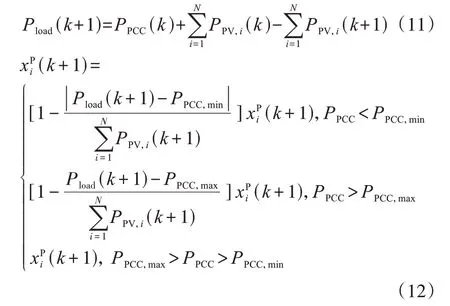
式中：Pload(k+1)為第k+1次迭代計算得到的臺區有功負荷；Pload(k)為第k次迭代PCC點有功功率；為臺區所有PV有功出力之和；PPV，i(k+1)為經過式（9）更新后臺區所有PV下一刻有功出力。低壓臺區與上級電網可交換無功的容量取決于變壓器剩余容量。根據式（9）和式（12）得有功功率控制后的此時PCC點無功功率上送最大值QPCC，max、上送最小值QPCC，min為：

式中：Qload(k+1)為第k+1次迭代計算所得臺區無功負荷；ST為臺區變壓器容量；QPCC(k)為第k次迭代PCC點無功功率；為臺區所有PV無功出力；為經過（10）更新后臺區所有PV下一刻無功出力。基于式（13）—（14），配變容量約束下無功功率利用率由式（15）進行更新。

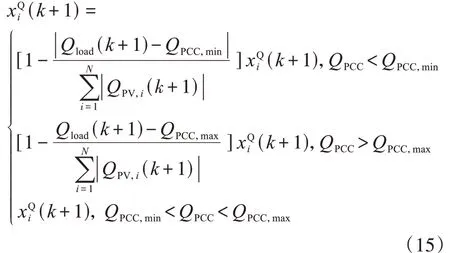
將式（12）、（15）代入式（9）、（10）得配變負載約束下各PV的有功功率、無功功率。綜上，低壓配電網邊端功率-電壓控制流程如圖2所示。

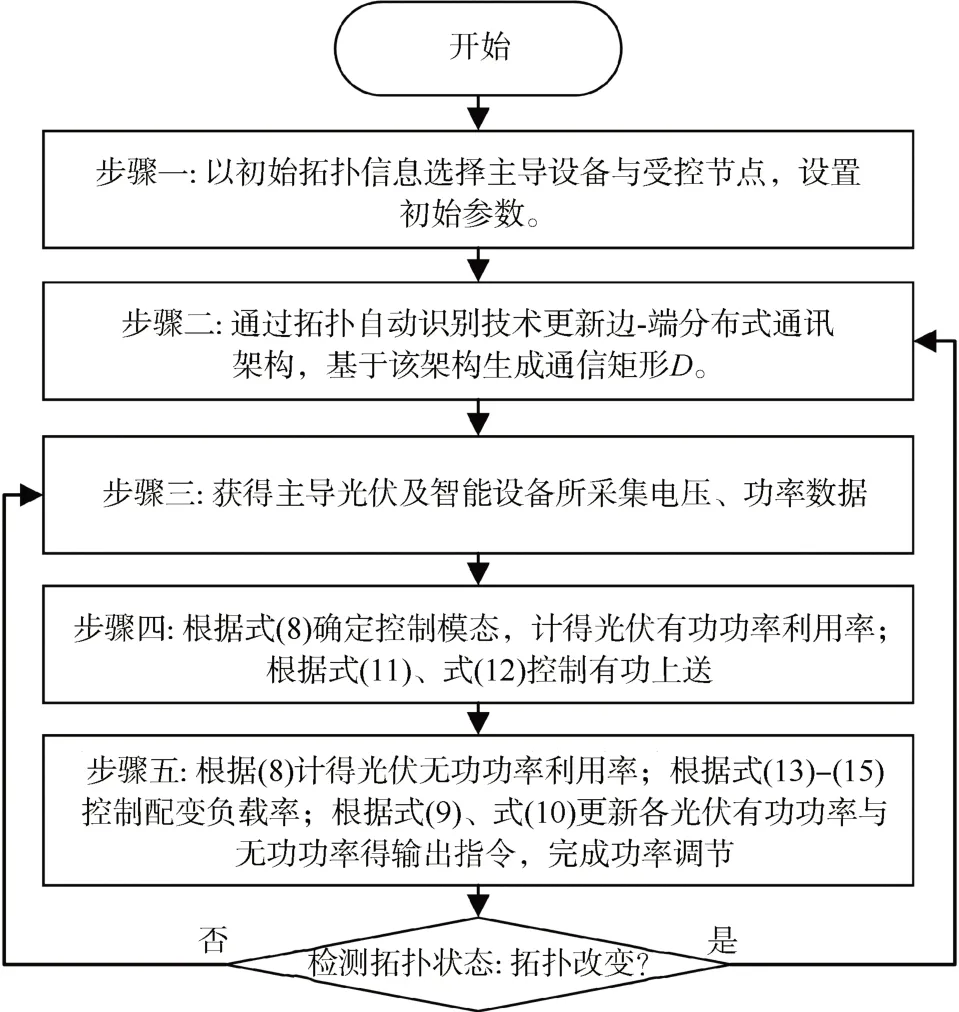
圖2 分布式模型的控制流程Fig.2 Controlprocess of distributed model

3 邊端功率-電壓模型參數設置

3.1 受控節點選擇原則

以功率利用率為一致性變量進行出力計算時，控制組內容量差異大的光伏設備因輸出功率差值過大，主導PV及受控節點的選擇將影響饋線的節點電壓平均水平。以節點1為首端節點、節點N為末端節點、含上游節點j、下游節點k（節點集合為｛1，2，···，j-1，j，j+1，··，k-1，k，k+1，··，N｝）的放射狀配電網饋線注入有功功率為例討論。

1）下游節點k接大容量光伏，上游節點j接小容量光伏。無論受控節點為k或j，在有功功率利用率x k=x j下存在可視ΔP=ΔP k-ΔP j注入下游節點k。根據DistFlow方程［13］，可推導得：

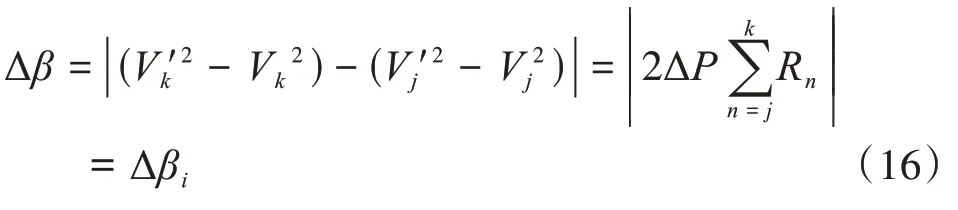
式中：Δβ為衡量兩個節點電壓在ΔP注入前后自身電壓增幅差異的變量；V j、V k為節點j、k無光伏接入電壓值；V'k、V'j為接入光伏后電壓值；R n為與節點n相連節點到節點n的等值電阻。此時，無論節點注入功率或流出功率，當上游節點j為受控節點，較大的Δβ1使下游節點k存在更大的越上下限風險。此時，考慮選擇接大容量光伏的下游節點k作為受控節點。相同容量PV均勻分布的情況同理。

2）下游節點k接小容量光伏，上游受控節點j接大容量光伏。無論受控節點為k或j，在x k=x j時存在此時視ΔP=ΔP j-ΔP k注入上游節點j，可推導得關系：

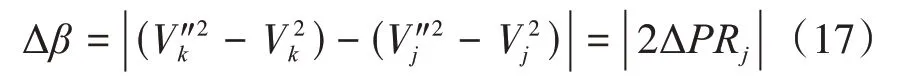
綜上，若PV容量分布均勻或下游安裝容量偏大，考慮以下游節點作為受控節點。

3.2 通訊矩陣權值優化及穩定性分析

對于系統內含有n個節點的通信拓撲可視為有向圖G=(V，E)。其中，為有限非空節點集，邊集E?V×V為點集的集合。對于控制率式（1）所示協議，狀態量迭代格式、無向通信網絡下通信矩陣D的元素di j表達為［23］：

式中：x為設備狀態量矩陣；I為單位矩陣；L為拉普拉斯矩陣；u為外來信號矩陣；σ為外來信號控制矩陣；mi為設備i的度，若其鄰接n個設備，則m i=n；α為變換系數。基于此，最小化該系統以D為優化變量的譜半徑可實現快速線性迭代。由式（18）可得矩陣D以L形式的特征值λ：

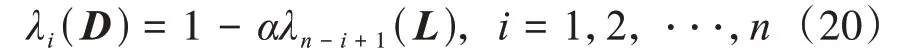
此時使系統收斂的α取值范圍及最優解α*為［25］：

式中：λn-1(L)為矩陣L的第n-1大特征值，如λ1=由此計算所有控制分組基于拉普拉斯矩陣L的通信拓撲優化權值，且所有控制分組通信矩陣D的譜半徑小于1，即系統收斂。同時，基于式（1）的跟隨設備狀態量可改寫為：

考慮跟隨設備i與主導設備之間狀態誤差ei（k）并建立誤差系統

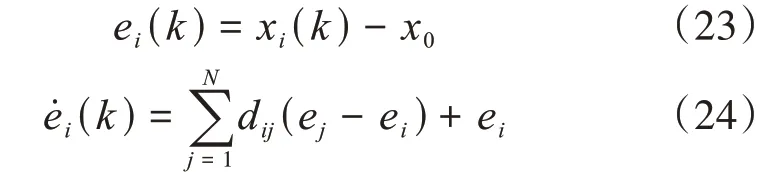
式中：x0為主導者的狀態，假設為常數；e j為設備i的鄰接設備j的狀態誤差。運用李雅普諾夫函數及圖論定理來證明系統應用算法（1）能夠實現有限時間一致性。有引理如下。

1）引理1［26］：對于給定無向拓撲圖G，若存在函數φ：R2→R滿足φ(xi，xj)=-φ(x j，xi)，?I，j∈；I，i≠j；那么就有一組數列y1，y2，???，y n滿足：

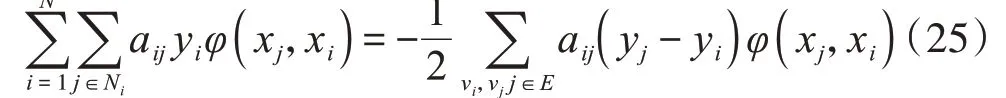
2）引理2［27］：非Lipschits連續非線性系統x?=f(x)、[f0=0]，若存在函數V(x)定義在原點區域C＞0，α∈(0，1)有V?(x)+C Vα≤0，那么原點是有限時間穩定的。

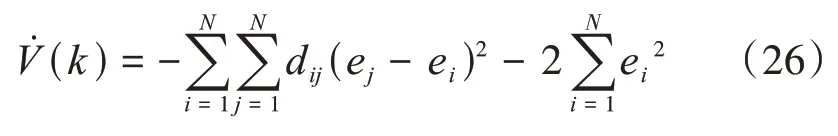
即

滿足引理2，則在基于拉普拉斯矩陣的權值優化下，系統可實現有限時間內一致性，為穩定系統。

4 仿真算例與結果分析

4.1 低壓配電網參數設置

以附錄圖A1臺區建立仿真算例。臺區某時間截面下負荷Pload=475.40 kW、Qload=217.23 kvar。選擇控制組末端PV為主導PV，其所在節點為有功控制節點。組1、2、3中集中智能電表箱為無功功率控制節點；組5的三相PV無功進行本地控制；組4以節點8作為無功功率控制節點。

為驗證邊端功率-電壓控制方法在不同條件下的適應性，本節基于PV在無光照環境到最大光照環境下的有功功率輸出范圍進行分析，定義光照系數G0∈[0 1]×PPV，max，即G0=0時PPV=0 W，G0=1時PPV=PPV，max。因此通過不同G0模擬PV出力在不同時段的變化情況。系統參數表1—2、圖3—4所示，大部分接入不同節點PV的滿額出力數倍大于節點負荷，多個節點電壓越下限，三相電壓偏差較大。

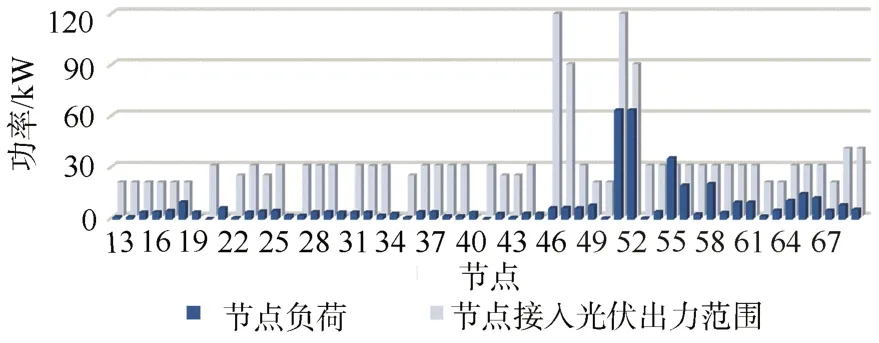
圖3 PV出力與節點負荷曲線Fig.3 Photovoltaic output and load of the nodes

表1 低壓臺區參數Tab.1 Parameters of low voltage network

表2 無PV接入時部分三相節點的U PVUR和PCC點參數Tab.2 U PVUR of three-phase nodes and PCC points without PV

4.2 系統收斂性分析

對該低壓配電網的PV進行有功/無功功率協調優化后，得到該網絡在不同光照環境下節點電壓幅值標幺值變化如圖5所示。

圖4 無PV接入下節點電壓幅值Fig.4 Voltage amplitude of the nodes without PV

圖5 不同PV出力下節點電壓幅值Fig.5 Voltage amplitude of the nodes under differentphotovoltaic output

以無光伏接入時低壓越限的節點8、52、67和配變功率為例，分析控制量在突變環境下的收斂性與系統穩定性。光照系數G0的變化序列為［0，0.4，0.8，0.6］，仿真結果如圖6所示。由圖6（a）可看出，低壓越限節點在配變負載約束下于迭代次數200內快速收斂，實現電壓控制目標。圖6（b）中，在配變負載約束下無功率上送越限情況下，快速收斂以實現臺區功率供需平衡。其中，由于在電壓越限時PV有功功率調度順序優先于無功功率調度，因此有功功率的收斂速度大于無功功率。

圖6 變化環境下節點電壓與交換功率曲線Fig.6 Voltage and exchanged power of the nodes under various conditions

4.3 拓撲自動識別下的即插即用功能

以控制組2中接入節點13、14的光伏故障退出為例，分析拓撲自動識別對控制效果的影響。在拓撲自動識別下重組通信矩陣D與普通退出的控制組2節點電壓幅值和不平衡度的對比如圖7所示。

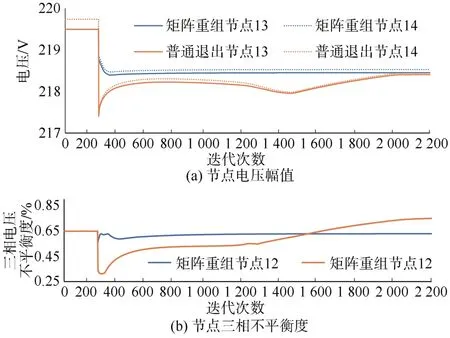
圖7 光伏故障退出下節點電壓幅值和不平衡度變化曲線Fig.7 Voltage amplitude and unbalance degree of the nodes when photovoltaic exits

發生故障退出光伏的控制系統由于錯誤獲取PV狀態而使系統收斂速度大幅降低，同時影響控制效果。如節點13、14電壓有一定程度的下降，同時被控制組2優化的節點12的不平衡度進一步上升。通過拓撲自動識別獲得PV狀態并由此重新生成通信矩陣D可保持系統在200次迭代內收斂，減輕故障影響，實現即插即用。

4.4 不同光照環境下控制方法對比仿真分析

以下以G0=0場景1、G0=0.5場景2、G0=1場景3對邊端電壓控制方法、文獻［11］控制方法與本地控制作對比分析。文獻［11］的控制分組為：控制組3構成GQ2組；控制組2及節點68、69接入光伏構成GV1組；控制組1構成GQ1組；節點51、52接入光伏構成GV3組；其余構成GV2組。本地控制方法以本文方法算例中主導DG接入節點為受控節點，Vset=1.0；其他節點不進行控制且不削減PV的有功功率輸出。該網絡下3種電壓控制方法的節點電壓和不平衡度如表3和圖8所示。

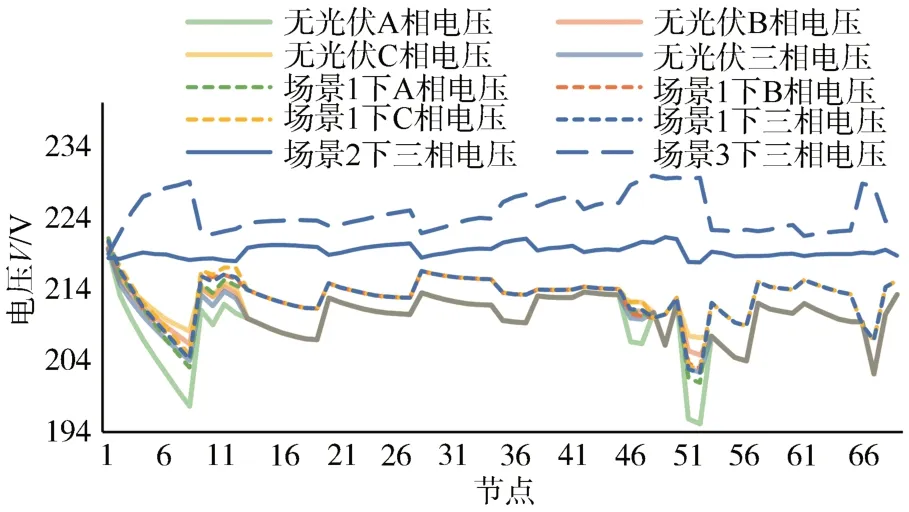
圖8 3種場景下節點電壓幅值Fig.8 voltage amplitude of the nodes under three conditions

如圖8和表3所示，邊端功率-電壓控制方法在G0=0.5、G0=1下無越限節點，三相節點UPVUR＜2%。由圖8中無光伏接入和場景1下三相節點電壓比較可知，在G0=0時，雖然PV無有功出力，但有大量冗余無功功率參與電壓控制與不平衡優化，臺區整體節點電壓偏差和三相電壓不平衡較無PV接入減小。

表3 3種場景下三相用戶節點電壓不平衡度Tab.3 Voltage unbalance of three-phase node under three conditions

如表4—6所示，本地控制無法控制三相不平衡，引起配電變壓器過載。其中，G0=1時，本地控制下變壓器負載率已超過100%；因無法控制節點電壓越上限，出現大量電壓越限節點如圖9所示。由于文獻［11］的臺區首端功率僅由兩個控制組調節，控制組的光伏容量與節點負荷影響組內節點電壓控制與功率交換控制效果，如表4—5所示，該方法控制下兩級電網功率交換越限。

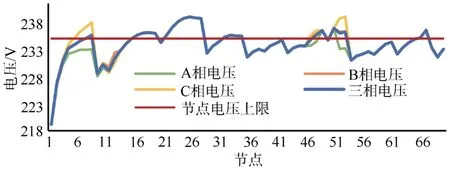
圖9 本地控制在G0=1下節點電壓幅值Fig.9 Voltage amplitude of the nodes when G0=1 by localcontrol

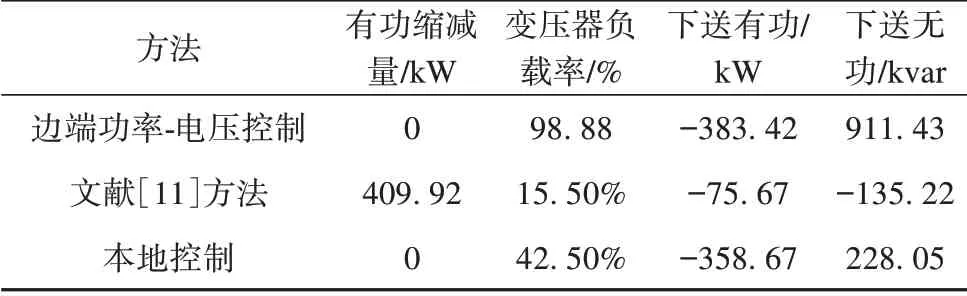
表4 G0=0.5下3種方法的仿真結果Tab.4 Simulation results of the three methods under G0=0.5

表5 G0=1下3種方法的仿真結果Tab.5 Simulation results of the three methods under G0=1

表6 G0=0下3種方法的仿真結果Tab.6 Simulation results of the three methods under G0=0

在3種情況下，邊端功率-電壓控制方法與文獻［11］方法所得電壓偏差相近，在G0=1和G0=0時遠低于本地控制。同時，本文方法在變壓器負載率低于100%要求下，通過控制模式變更保證可再生能

源利用率，如在G0=1時，有功功率縮減量低于文獻［11］方法，其中在G0=0.5下實現PV有功出力全消納，因此該方法有效提高臺區可再生能源消納能力。

4.5 拓撲自動識別下的即插即用功能

基于附錄圖A1的配電網系統，修改組2A相節點13、14、15、16和組3C相節點61、62、63、64無PV接入，一級分支中C相節點50、66無PV接入，臺區共接入40臺光伏發電系統。此時，組2、3和組5的PV接入在3個相序間存在較嚴重的不平衡，以此模擬單相PV隨機接入的極端情況。在G0=0、G0=0.5、G0=1時部分三相節點電壓平衡度和節點電壓幅值如圖10和表7所示。

圖10 40臺PV接入系統在3種光照下節點電壓幅值Fig.10 Nodes voltage amplitude under three irradiance when accessing 40 PVs

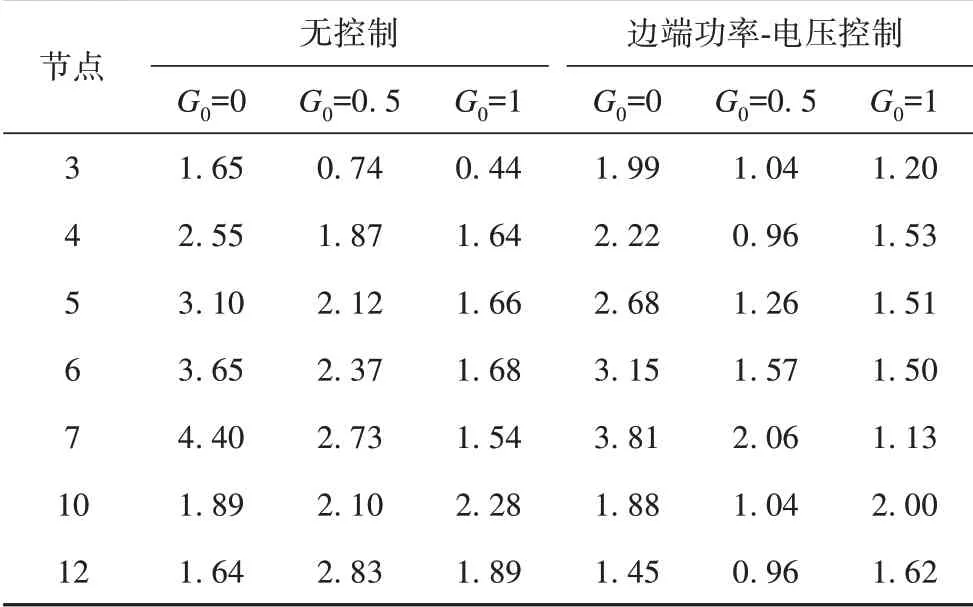
表7 40臺PV接入系統三相用戶節點電壓平衡度Tab.7 Voltage balance of three-phase when accessing 40 PVs

由于接入相序嚴重不均，且可調節功率減少，本文方法在控制不均勻隨機接入40臺PV的臺區節點電壓偏差較40臺接入大，如表7所示。為了滿足不平衡控制，在G0=0下對節點電壓抬升度較小。但本文方法對整體臺區電壓幅值控制和三相用戶節點不平衡度改善仍表現出良好的效果。

5 結論

本文針對低壓配電網在PV高滲透下反向潮流引起低壓運行問題，考慮對網絡拓撲、通信條件的依賴性和可再生能源消納，提出了低壓配電網邊端功率-電壓控制方法。結論如下。

1）通過拓撲自動識別的方法與智能終端共同建立“臺區智能終端-分支監測終端-用戶表箱-PV設備”分布式通信架構，可進一步降低臺區控制對網絡拓撲的依賴度，實現即插即用。

2）分布式通信架構下低壓配電網多模態控制模型可進一步提高臺區對分布式能源的消納能力。在提出的受控節點原則與權值優化下，系統的收斂性與穩定性得到證明。

3）在配電變壓器運行約束下的全光伏功率控制方法實現功率精準控制，有效避免了大量功率倒送導致配電變壓器過載的問題。