基于快速獨立分量分析與改進隨機子空間算法相結(jié)合的次同步振蕩模態(tài)辨識

王雨虹，宋志超，孟憲敬，孫少華

（1.遼寧工程技術(shù)大學電氣與控制工程學院，遼寧 葫蘆島 125105；2.開灤集團，河北 唐山 063000；3.國網(wǎng)寧德供電公司，福建 寧德 352100）

0 引言

近年來，我國風力發(fā)電總裝機容量不斷增加，為了適應能源賦存與消耗逆向分布的格局，大功率高電壓直流輸電在風電系統(tǒng)中得到了廣泛應用。輸電線路中串聯(lián)了大量的電容補償器，致使次同步振蕩（subsynchronous oscillation，SSO）問題日益突出［1-2］。輸電系統(tǒng)次同步振蕩的發(fā)生不僅會造成降低系統(tǒng)傳輸功率，嚴重時還可能導致風機脫網(wǎng)、發(fā)電機軸系斷裂的事故，對電力系統(tǒng)的穩(wěn)定運行有著嚴重的威脅。為此，需要快速、準確地辨識出次同步振蕩的各個模態(tài)，以便對次同步振蕩進行監(jiān)測、預警和抑制。

傳統(tǒng)的次同步振蕩分析方法多以系統(tǒng)整體模型為基礎(chǔ)，如頻率掃描法［3］、特征結(jié)構(gòu)分析法［4-6］、復轉(zhuǎn)矩系數(shù)分析法［7］等。然而，隨著電力系統(tǒng)規(guī)模的擴大，整體結(jié)構(gòu)復雜度的增加，難以建立完善的電力系統(tǒng)模型，使得穩(wěn)定性分析結(jié)果存在較大的誤差。近年來，廣域量測系統(tǒng)的成熟發(fā)展，為基于實測數(shù)據(jù)的次同步振蕩在線辨識提供了充足的條件［8-10］。文獻［11］采用小波去噪和Prony算法結(jié)合的辨識方法，雖能解決Prony算法抗噪性弱的問題，但在去噪中過于依賴閾值的選取，易產(chǎn)生虛假模態(tài)或模態(tài)遺漏現(xiàn)象。文獻［12］在次同步振蕩辨識中采用總體最小二乘-旋轉(zhuǎn)不變算法，該方法在辨識速度和精度上具有優(yōu)勢，但在強噪聲環(huán)境下辨識結(jié)果存在較大誤差。為此文獻［13］引入Hankel矩陣來改進總體最小二乘-旋轉(zhuǎn)不變算法，降低噪聲干擾，但該算法存在模態(tài)階數(shù)定階難的問題。文獻［14］采用的遞推隨機子空間辨識方法雖能提高辨識速度，但隨機子空間算法的應用必須具備模態(tài)階數(shù)確定的前提。文獻［15］采用穩(wěn)定圖法來對隨機子空間算法定階，但由噪聲引起的穩(wěn)定極點并非真實情況的穩(wěn)定點，穩(wěn)定圖無法剔除噪聲模態(tài)。

由于電網(wǎng)中存在大量電力電子設(shè)備，造成實測信號中包含強干擾噪聲，而噪聲的干擾會讓辨識方法出現(xiàn)系統(tǒng)階數(shù)難以確定的問題。當系統(tǒng)模態(tài)階數(shù)過高會包含噪聲子空間存在虛假模態(tài)，模態(tài)階數(shù)過低會遺漏信號模態(tài)。因此，對實測信號有效地降噪進而準確地確定系統(tǒng)模態(tài)階數(shù)在次同步振蕩辨識中至關(guān)重要。為此，本文提出一種將快速獨立分量分析技術(shù)（fast independent component analysis，F(xiàn)astICA）和基于精確模態(tài)定階改進隨機子空間算法（stochastic subspace identification，SSI）相結(jié)合的方法。首先，用快速獨立分量分析技術(shù)對實測信號進行噪聲和原信號的分離預處理［16］，將處理后的信號輸入隨機子空間算法，針對隨機子空間算法難以準確估計模態(tài)階數(shù)的問題［17］，用精確模態(tài)定階的方法予以改進，避免出現(xiàn)虛假模態(tài)和模態(tài)遺漏的現(xiàn)象，確定信號中的主要模態(tài)，進而辨識出各個模態(tài)參數(shù)。由風電場仿真算例和實際電網(wǎng)數(shù)據(jù)驗證了該方法在強噪聲環(huán)境下能夠有效地進行去噪預處理，并且準確地計算出模態(tài)階數(shù)，快速辨識出振蕩的主要模態(tài)參數(shù)。

1 快速獨立分量分析技術(shù)與精確模態(tài)定階改進隨機子空間算法的基本原理

1.1 快速獨立分量分析技術(shù)

快速獨立分量分析技術(shù)是一種快速尋優(yōu)迭代算法，在信號的盲源分離和特征提取方面應用廣泛。廣域量測系統(tǒng)從電網(wǎng)采集的信號數(shù)據(jù)都會包含由快速勵磁、負荷功率隨機變化產(chǎn)生的干擾噪聲。對于這種混雜信號，快速獨立分量分析算法能夠有效地將噪源信號分離，起到降噪的作用［18］。

次同步振蕩采樣信號由Y表示，線性模型為：

式中：A為混合矩陣；S為獨立源向量。

快速獨立分量分析技術(shù)的任務是在A和S未知的情況下構(gòu)建解混矩陣B，將原信號從采樣信號中比較完善地分離出來。表達式如下：

若要使?最大程度逼近S，只需要滿足解混矩陣B最佳近似于A-1。

在隨機變量中，用負熵來度量非高斯性［19］。負熵表達式近似為：

式中：E(?)為均值函數(shù)；G(?)為非線性函數(shù)；s為獨立源信號；sGauss為s的高斯分布向量。

依據(jù)極大化非高斯性原理，通過負熵使目標函數(shù)最大化，得到最佳估計解混矩陣，對源信號進行有效地分離［20］。以負熵最大作為搜尋方向，其迭代公式為：

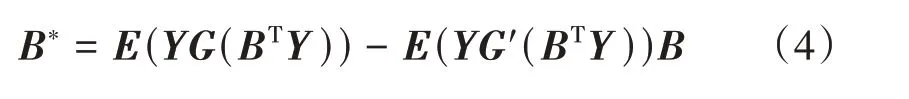
式中B*為中間矩陣。

標準化處理得到解混矩陣，進而從采樣信號中分離出原信號。

1.2 基于精確模態(tài)定階改進的隨機子空間算法

1.2.1 隨機子空間算法

將由快速獨立分量分析技術(shù)分離而來的原信號y k構(gòu)造Hankel矩陣。

式中：i=2n，n為系統(tǒng)階數(shù)；j為量測量采樣數(shù)。令Y-f=Y i+1|2i-1和Y+p=Y0|i。

使用Hankel子矩陣確定投影矩陣P i。

對投影矩陣P i進行奇異值分解。

形成擴展可觀測矩陣Γi。

計算卡爾曼濾波狀態(tài)序列。

確定系統(tǒng)狀態(tài)矩陣并且對其進行特征值分解。

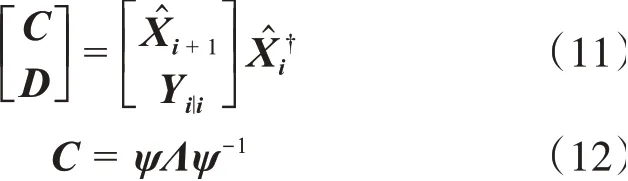
式中：C為系統(tǒng)狀態(tài)矩陣；Λ=diag(λi)∈Rn×n，i=1，2，…，n；λi、ψ分別為離散系統(tǒng)特征值和特征向量矩陣。

根據(jù)系統(tǒng)連續(xù)特征值ηi計算次同步振蕩的頻率fk、阻尼比ξi和衰減因子?i。

式中：Δt為采樣時間間隔；ηi*和ηi互為共軛；|·|表示模。

1.2.2 精確模態(tài)定階法

隨機子空間算法雖對諸多振蕩模態(tài)具有很好的識別效果，但是在含噪信號中對模態(tài)階數(shù)的選取要求較高，難以識別出信號的主要模態(tài)［21-22］，所以精確地估計系統(tǒng)模態(tài)階數(shù)是該方法的關(guān)鍵［23］。文獻［24］中直接用奇異值分解確定系統(tǒng)階數(shù)，但在含噪信號中奇異值并不能很好地表示各個模態(tài)的能量分布，會有過多的虛假模態(tài)，使辨識結(jié)果存在較大誤差。文獻［25］提出用奇異熵來確定系統(tǒng)階數(shù)，這種方法過度依賴閾值的選取，在信噪比不同的信號中，閾值選取困難，在強噪聲干擾環(huán)境下，會遺漏信號模態(tài)。

本文將精確模態(tài)定階的方法應用到隨機子空間算法中，對其定階難的問題予以改進。在次同步振蕩信號辨識中，特征值的大小分布能夠代表信號的能量分布，根據(jù)特征值的大小和分布規(guī)律，設(shè)定兩個判據(jù)，對模型階數(shù)精確定階。

1）特征值的相對差值最大。

由系統(tǒng)狀態(tài)矩陣分解而來的特征值能夠顯著地代表次同步振蕩信號的功率譜密度，因此在信號和噪聲子空間的接合點處會有顯著的變化。按照其能量大小的分布，較大的特征值表示包含主要模態(tài)的信號，即信號子空間；較小的特征值表示噪聲信號，即噪聲子空間。按降序排列的特征值從最大值逐漸減小，直到λi驟然降低，隨后λi+1保持很小的能量且緩慢地降低。說明λi是信號子空間和噪聲子空間的界點，即i為系統(tǒng)模態(tài)的階數(shù)。定義連續(xù)特征值λi的相對差值（relative difference，RD）來確定信號子空間和噪聲子空間的界點。

當相對差值取到最大值時，i即為系統(tǒng)的實際模態(tài)階數(shù)。此時，已經(jīng)能夠解決由噪聲帶來的虛假模態(tài)問題，準確地確定系統(tǒng)模態(tài)階數(shù)。然而當信號中出現(xiàn)一個或多個主要模態(tài)，并且其能量遠大于其他振蕩模態(tài)時，系統(tǒng)可能會將取得最大相對差值對應的階數(shù)確定為模態(tài)階數(shù)。實際階數(shù)對應的相對差值并非最大相對差值，因此出現(xiàn)模態(tài)遺漏現(xiàn)象。為避免這種現(xiàn)象的發(fā)生，用第二判據(jù)進行驗證。

2）相對差值對應的特征值屬于信號子空間

在第一判據(jù)中選取多個較大相對差值對應的階數(shù)作為候選階數(shù)，候選階數(shù)所對應的特征值由大到小依次用式（18）進行驗證。

式中：l為系統(tǒng)模態(tài)的候選階數(shù)；λi為相應的特征值；α為靈敏因子，取值在2—4。本文靈敏因子取值為4，因較大的靈敏因子對應較高的靈敏度，即使信號中模態(tài)分量較小也能夠被檢測出，做到不遺漏模態(tài)。

精確模態(tài)定階法以特征值的相對差值最大作為第一判據(jù)，避免系統(tǒng)模態(tài)階數(shù)過高，產(chǎn)生虛假模態(tài)；以相對差值對應的特征值屬于信號子空間作為第二判據(jù)，避免系統(tǒng)模態(tài)階數(shù)過低，出現(xiàn)模態(tài)遺漏現(xiàn)象。上述兩個判據(jù)能夠很好地解決在噪聲環(huán)境中模態(tài)定階難和閾值難選取的問題，極大地提高了定階的準確性。

2 基于快速獨立分量分析技術(shù)和改進隨機子空間算法對振蕩模態(tài)參數(shù)的辨識

2.1 算法流程

以廣域量測信號作為采樣信號，對包含噪聲和原信號的采樣信號用快速獨立分量分析技術(shù)進行噪源信號的分離，減少強噪聲的干擾；采樣信號經(jīng)過預處理后，依然存在干擾噪聲，為了提高辨識精度，用精確模態(tài)定階法改進隨機子空間算法，來精確計算系統(tǒng)模態(tài)階數(shù)，避免出現(xiàn)虛假模態(tài)和模態(tài)遺漏的現(xiàn)象，確定主要模態(tài)，準確地辨識各個模態(tài)參數(shù)。具體步驟如圖1所示。

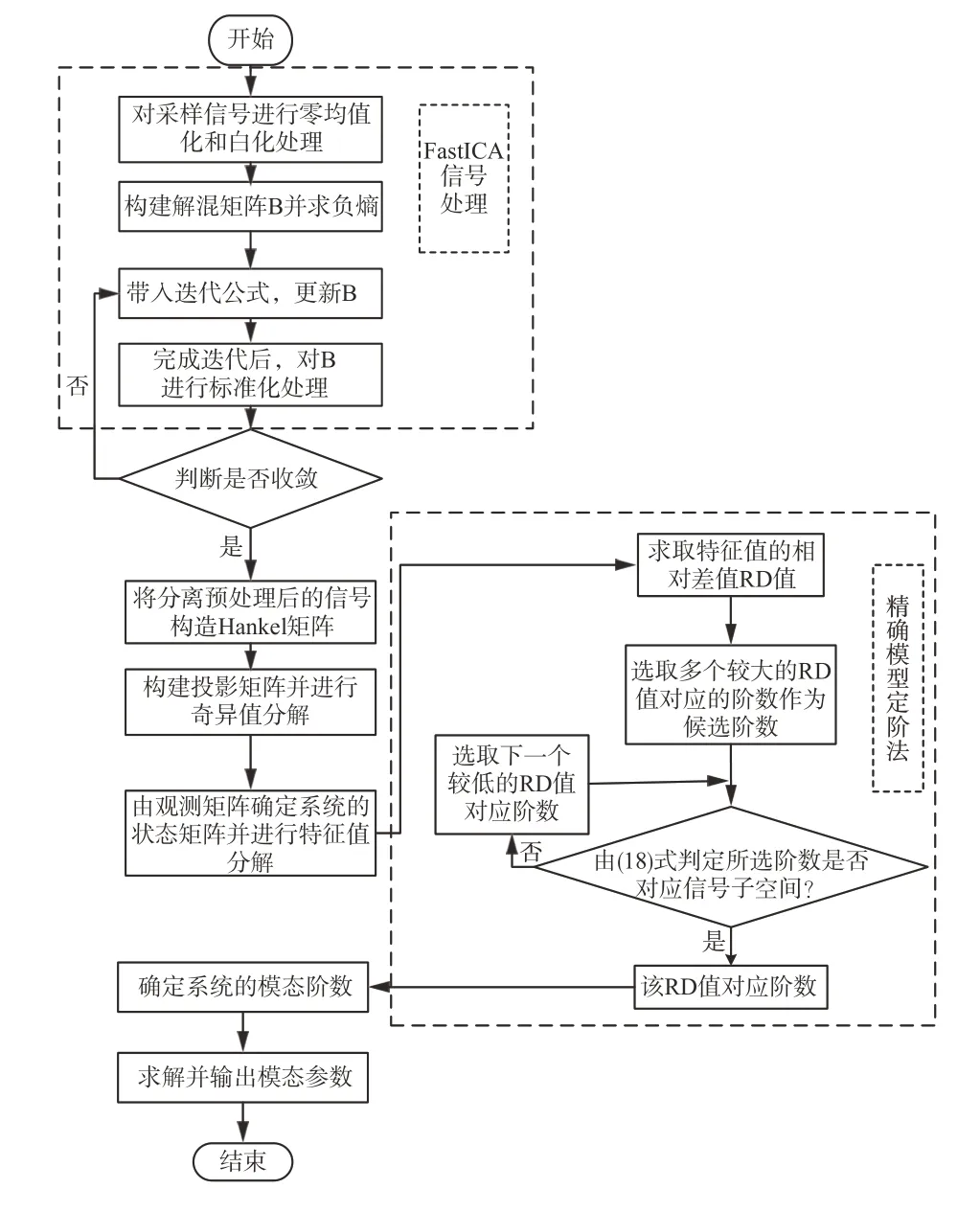
圖1 方法流程圖Fig.1 Method flow chart

步驟1：以廣域量測得到的采樣信號輸入信號，并對其進行零均值化和白化處理。

步驟2：確定需要估計分量的個數(shù)，設(shè)定迭代次數(shù)。

步驟3：構(gòu)建解混矩陣，在負熵最大的方向進行迭代計算。

步驟4：確定收斂后的解混矩陣，對采樣信號分離出噪聲信號和原信號。

步驟5：由含微弱噪聲的原信號構(gòu)造Hankel矩陣，并且由觀測矩陣確定系統(tǒng)的狀態(tài)矩陣，進行特征值分解。

步驟6：為了準確地得出系統(tǒng)模態(tài)階數(shù)，用精確模態(tài)定階法改進隨機子空間算法。對特征值求取相對差值，以此來確定信號子空間和噪聲子空間臨界點。

步驟7：選取系統(tǒng)模態(tài)的候選階數(shù)，并用式（18）來判別所選階數(shù)是否對應主要信號子空間。

步驟8：確定模態(tài)階數(shù)，進而得出各個振蕩模式的特征參數(shù)。

2.2 評價標準

為比較辨識后的重構(gòu)信號和原信號的擬合程度，引入評價標準—擬合精度（accuracy of fitting index，AOF）。

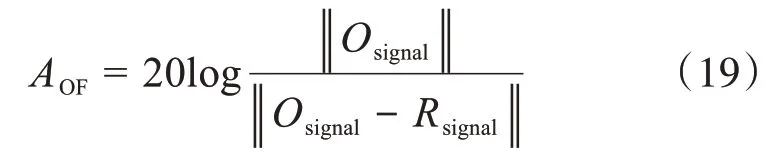
式中：Osignal為原信號；Rsignal為重構(gòu)信號；‖‖·表示二范數(shù)；AOF單位為dB。正常而言，當AOF≥10時就滿足擬合精度的要求。

3 算例分析

3.1 理想算例

構(gòu)造理想信號x(t)：

其中：

該信號的主要參數(shù)如表1所示。

表1 理想信號參數(shù)(模型階數(shù)為3)Tab.1 Idealsignal parameters with a modalorder of three

為了驗證本文方法在強噪聲環(huán)境下的去噪效果，在理想信號式（21）中加入高斯白噪聲，圖2為理想信號和加噪信號。利用快速獨立分量分析技術(shù)對信號進行預處理，圖3為分離后的信號和理想信號，圖4為分離后的噪聲信號。通過觀察圖3中兩條曲線，可以很明顯地看出原信號能被較好地分離出來，信噪比也由原來的5 dB提高到了19.574 1 dB，說明快速獨立分量分析技術(shù)能夠?qū)胄盘栠M行有效的預處理。

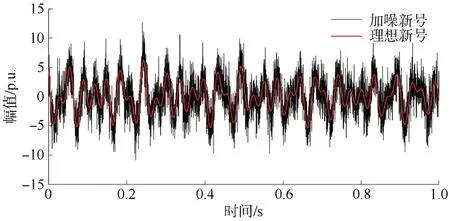
圖2 理想信號和加噪信號Fig.2 Idealand noise-added signals

圖3 分離后的信號和理想信號Fig.3 Separated signaland idealsignal

圖4 噪聲信號Fig.4 Noise signal

分別采用本文方法、基于集合經(jīng)驗模態(tài)分解（ensemble empirical mode decomposition，EEMD）［26］的矩陣束算法（matrix pencil，MP）和特征值系統(tǒng)實現(xiàn)算法（eigenvalue system realization algorithm，ERA），對添加了5 dB、15 dB高斯白噪聲的理想信號算例進行辨識，結(jié)果如表2所示。

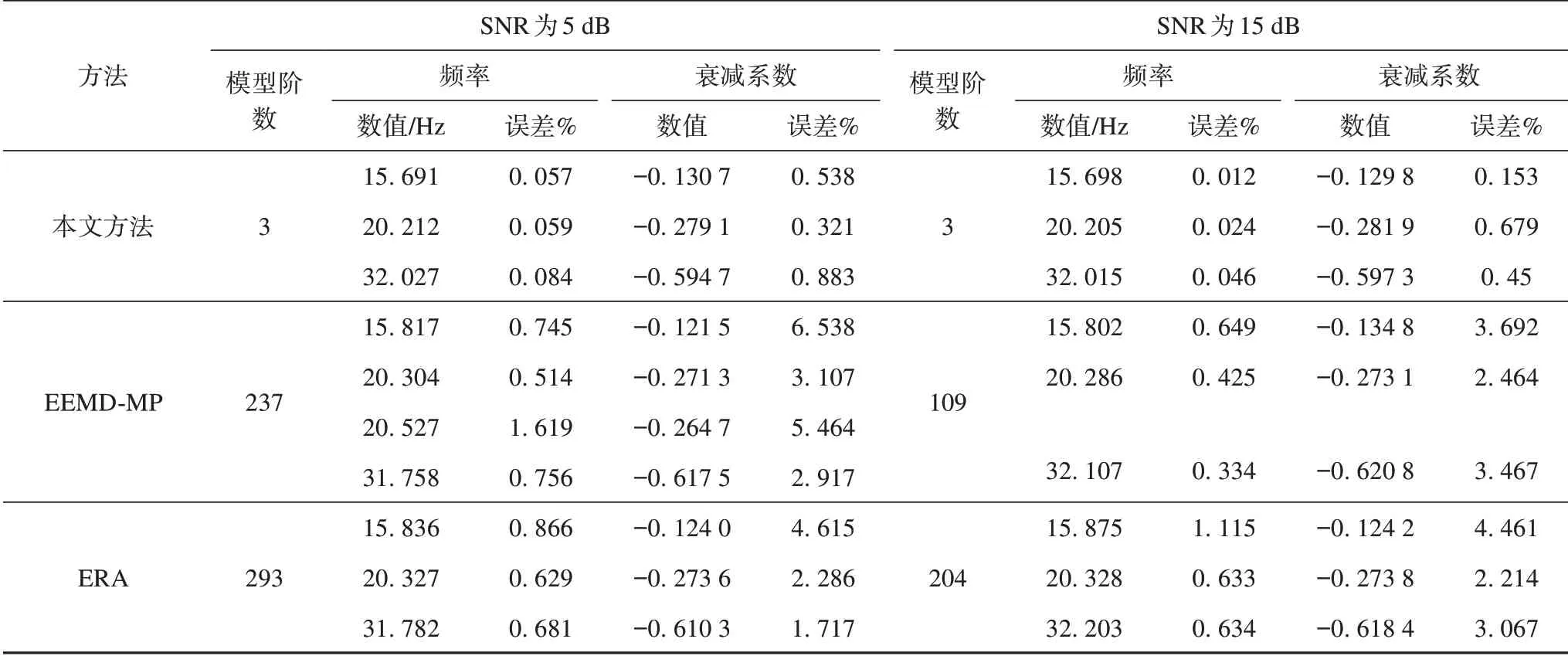
表2 辨識方法對比Tab.2 Comparison of identification methods

由表2可以看出，在模型定階中，基于集合經(jīng)驗模態(tài)分解的矩陣束算法（EEMD-MP）和ERA算法確定的模型階數(shù)均存在過高現(xiàn)象，在信噪比（signal noise ratio，SNR）為5 dB的信號中，EEMD-MP法出現(xiàn)了虛假模態(tài)的現(xiàn)象。ERA算法雖然能夠辨識出各個模態(tài)特征，但模型階數(shù)估算過高導致辨識精度上誤差較大。相較而言本文方法在含噪信號中不僅能夠有效準確地確定模態(tài)階數(shù)，更精確地辨識出各個模態(tài)的參數(shù)，對各個振蕩模態(tài)的頻率、衰減因子辨識精度更高。說明本文方法能夠有效地去除噪聲的干擾，并且準確地計算模態(tài)階數(shù)，進而在誤差更小的情況下辨識出信號中各個模態(tài)的頻率和衰減系數(shù)。

為了進一步驗證本文方法在去噪和辨識精度方面有更好的優(yōu)越性，作出加噪信號經(jīng)本文方法、EEMD-MP算法和ERA算法辨識后的擬合曲線，并計算擬合精度，其結(jié)果如圖5、表3所示。可以看出，與其他兩種方法相比，加噪后的理想信號經(jīng)本文方法辨識后與原始信號擬合精度更高，從而使得擬合曲線和原信號更吻合。

表3 擬合精度Tab.3 Fitting accuracy

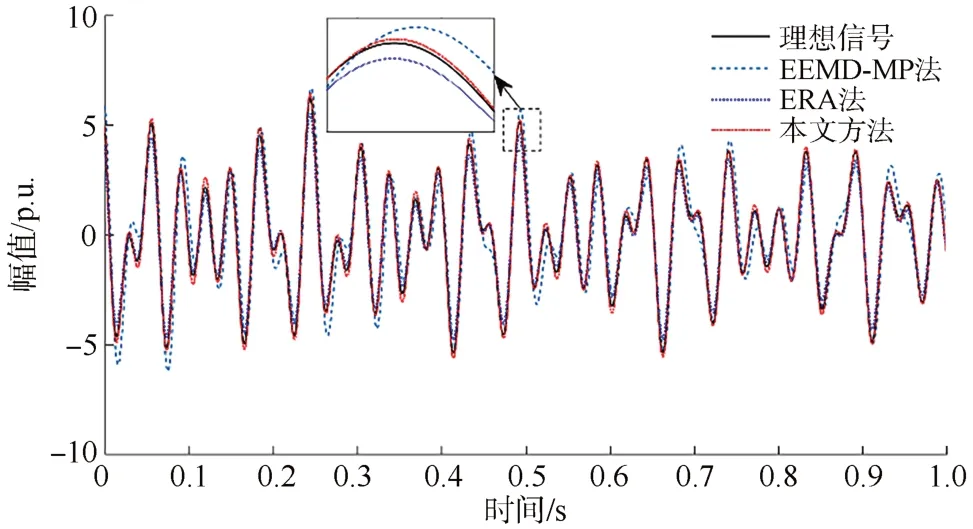
圖5 擬合曲線Fig.5 Fitting curves

表4為用本文方法和隨機子空間算法對不同的SNR值下的信號進行模型階數(shù)估計和完成時間的對比。相較于隨機子空間法，本文方法對模態(tài)階數(shù)估計更為精確，并且具有更快的辨識速度。

表4 模態(tài)階數(shù)和完成時間Tab.4 Mode order and completion time

3.2 風電場標準模型

為進一步驗證本文方法在次同步振蕩參數(shù)辨識時的可行性，在PSCAD平臺搭建雙饋風電場標準模型進行仿真分析，圖6為系統(tǒng)結(jié)構(gòu)圖。模型有5個扭振頻率：15.70、20.22、25.55、32.30、47.45 Hz。

圖6 雙饋風電場標準模型結(jié)構(gòu)圖Fig.6 Structure diagram of standard modelof doubly fed wind farm

仿真條件：仿真時間設(shè)為2 s，在t=1.5 s時，施加擾動使其發(fā)生三相短路故障，受到擾動的系統(tǒng)其變流器與電網(wǎng)側(cè)發(fā)生動態(tài)交互作用，引起次同步振蕩。取系統(tǒng)電壓作為分析信號，如圖7所示。

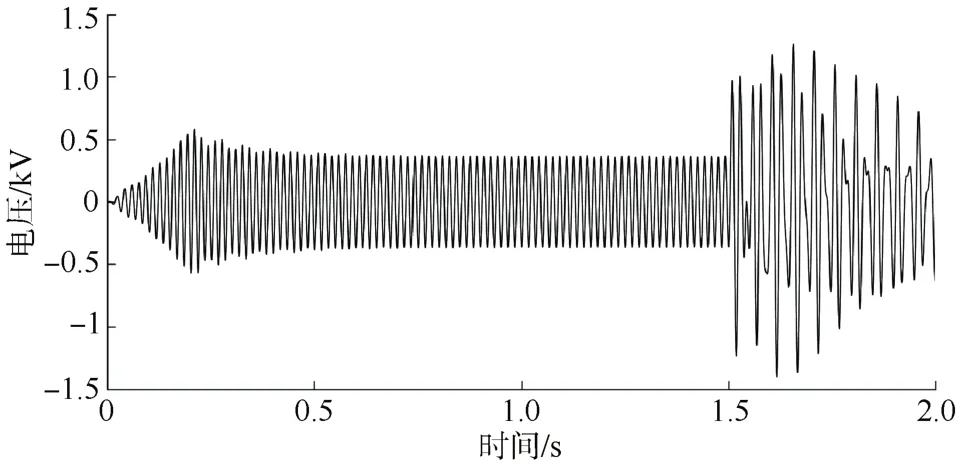
圖7 系統(tǒng)電壓Fig.7 System voltage

為貼近現(xiàn)場的實際情況，在t=1.5～2 s時段的電壓信號中加入SNR值為5 dB的白噪聲，加噪后的信號和原信號如圖8所示。圖9為含噪信號經(jīng)快速獨立分量分析算法預處理后得到的分離信號和原信號，可以看出該算法幾乎完整地將原信號分離出來，SNR值也由原來的5 dB提高到了16.734 9 dB，說明確實起到了較好的降噪作用。

圖8 加噪信號和局部原信號Fig.8 Noisy signal and localoriginalsignal

圖9 分離后的信號和原信號Fig.9 Separated signaland idealsignal

對加噪信號分別采用改進MP算法［27］、改進Prony算法［28］和本文方法進行辨識，其結(jié)果如表5所示。由表5可知，改進的Prony算法由于受到噪聲影響，沒有辨識出20.22 Hz振蕩模式，并且在別的振蕩模式上所提方法在辨識精度上更優(yōu)越。而改進的矩陣束算法，因為對系統(tǒng)模態(tài)階數(shù)定階偏高，致使辨識結(jié)果中出現(xiàn)了虛假模態(tài)。相較之下，所提方法在對模態(tài)階數(shù)準確定階的前提下，能夠準確地辨識出系統(tǒng)的各個模態(tài)，并且擬合精度更高。

表5 辨識結(jié)果對比Tab.5 Comparison of identification results

3.3 實際工程算例

實際算例采用新疆某風電場輸電系統(tǒng)，其網(wǎng)絡(luò)構(gòu)架圖如圖10所示。取ZGH、XH和TD 3個相鄰風電場實測數(shù)據(jù)來驗證。其中圖11為ZGH、XH和TD 3風電場實測電流信號和局部放大圖。由圖11可以看出，實測數(shù)據(jù)在10 s時開始發(fā)生持續(xù)振蕩，并且在15.8 s時振蕩幅度增大。

圖10 風電場架構(gòu)圖Fig.10 Wind farm architecture diagram

圖11 ZGH、XH、TD風電場電流Fig.11 Current of ZGH,XH and TD wind farms

將3個風電場電流作為分析信號，然后用本文方法對采樣信號進行降噪處理和辨識，選取20—21 s局部放大，如圖12所示。由圖12很明顯可以看出，與實測信號相比，經(jīng)快速獨立分量分析技術(shù)去噪后的信號其由噪聲造成的毛刺狀得到顯著的減少，降噪后的波形完整光滑，說明對于實測信號該方法也能起到很好的降噪作用。

圖12 ZGH、XH、TD風電場局部電流分離信號和實際信號Fig.12 Localcurrent separation signaland actualsignalof ZGH,XH and TD wind farms

將去噪后的信號輸入改進的隨機子空間算法中進行模態(tài)參數(shù)的辨識，結(jié)果如表6所示。由表6辨識結(jié)果可知，文中所用方法能夠辨識出3個風電場中存在6個次同步振蕩模態(tài)，且衰減系數(shù)均為正值，說明電流呈現(xiàn)振蕩發(fā)散狀態(tài)，與電場實測數(shù)據(jù)波形相符。由此可得，本文方法能夠快速有效地辨識出該風電場的各個振蕩模式及其參數(shù)。

表6 辨識結(jié)果Tab.6 Identification results

4 結(jié)論

針對次同步振蕩在線辨識中在強噪聲環(huán)境下系統(tǒng)模態(tài)定階難的問題，提出一種快速獨立分量分析技術(shù)和精確模態(tài)定階改進隨機子空間相結(jié)合的次同步振蕩辨識方法。首先，用快速獨立分量分析技術(shù)對采樣信號進行預處理，分離出原信號，然后用精確模態(tài)定階的思想來計算信號的模態(tài)階數(shù)，以此來確定信號的主要模態(tài)，最后快速準確地辨識出信號的模態(tài)參數(shù)，判斷是否發(fā)生次同步振蕩現(xiàn)象。

通過仿真算例和實際工程算例進行驗證，結(jié)果表明對于強噪聲環(huán)境里的信號，該方法不僅能夠有效地分離出原信號，還能夠剔除虛假信號做到不遺漏重要的模態(tài)，提高了抗噪性、辨識速度和辨識精度，并且能夠準確地辨識出實際輸電系統(tǒng)的各個振蕩模式，為次同步振蕩的抑制措施奠定了基礎(chǔ)。