塔式太陽能熔鹽吸熱器光-熱-力耦合模擬及性能分析

賈朋森，王 坤，張 翔，楊 歷，閔春華

（1.河北工業大學 能源與環境工程學院，天津 300401；2.河北工業大學 熱能科學與能源清潔利用河北省重點實驗室，天津 300401）

0 引言

外露式吸熱器因其耐高溫、結構簡單的優點成為塔式太陽能發電系統中最具發展前景的吸熱器形式之一。然而，塔式太陽能熱發電（Solar Power Tower，SPT）系統所聚焦太陽能流在吸熱器表面分布極不均勻，這也對吸熱器安全高效運行提出了挑戰[1-2]。局部過熱導致外部吸收涂層的退化和內部傳熱流體的分解[3-4]；溫度梯度過大將會使導致吸熱管道較大的熱應力和熱變形，甚至造成吸熱器結構故障[5-6]。

Du等[5]和Marugán-Cruz等[7]在吸熱管表面熱流密度遵循余弦分布的假設條件下分析了吸熱管的應力特性，探討了單管的應力分布與能流密度的關系，指出最大熱應力位于吸熱管能流密度最高處。Sánchez等[8]進一步在每個吸熱管排中選取一根吸熱管并進行串聯，研究了整個吸熱器中熔鹽溫度的變化及吸熱器周向應力變化。Xu等[9]則對整個吸熱器的熱效率和表面溫度隨質量流量和DNI（Direct Normal Irradiation）的變化進行了研究。在他們的研究中，通過引入經驗關聯式來計算吸熱器與外界環境的對流換熱損失，忽略了對流換熱系數沿吸熱器周向的變化。隨后，Christian等[10]和Uhlig等[11]提出將吸熱管排簡化成矩形的通道管板，并且通過引入風域計算吸熱器與外界環境的對流換熱損失，但由于將吸熱管排簡化為管板，未能對吸熱管排的熱應力進行分析。Wang等[12]基于蒙特卡洛光線追蹤法（Monte Carlo Ray Tracing，MCRT）、有限體積法（Finite Volume Method，FVM）和有限元法（Finite Element Method，FEM）建立了太陽能吸熱器的光-熱-力耦合模型，研究了不同位置吸熱管在不同時刻和熱流密度下的光熱轉換性能及應力特性。

本文在前人研究方法的基礎上，基于MCRT、FVM、FEM建立了外露式太陽能吸熱器的光-熱-力耦合數值模型，并通過與美國Solar Two電站的實驗數據進行對比完成了模型驗證，在此基礎上探討了在非均勻熱流邊界及外部強制對流換熱條件下吸熱器的光熱轉換性能及應力特性，重點討論了多點聚焦下吸熱器溫度場的時空變化規律及應力分布。

1 計算模型及熔鹽物性

1.1 物理模型

本文以Solar Two塔式熔鹽電站采用的圓柱形外露管式吸熱器為例進行分析。吸熱器以熔鹽Solar Salt作為吸熱工質，包括2個熔鹽回路，每個回路包括12個串聯的吸熱管排，如圖1所示。吸熱管的表面涂有黑色Pyromark選擇性吸光涂層[13]。表1給出了吸熱器物理模型的詳細信息。圖2給出了詳細的熔鹽流動路徑、管排編號和吸熱管編號。在回路1中，低溫熔鹽首先從編號為W1的管排入口流入，流經管排W6，再從管排W6出口流出，進入管排E7，最后從管排E12流出，如圖1中紅色回路線所示。回路2的熔鹽流動方式與回路1類似。

圖1 Solar Two吸熱器示意圖（左側），帶有面板編號的流動回路圖和管道細節（右側）Fig.1 Schematic diagram of Solar Two receiver(left),and the flow circuit diagram with panel numbers and tube details(right)

表1 Solar Two圓柱形吸熱器的幾何參數Tab.1 Geometric parameters of Solar Two receiver

圖2 外露式吸熱器熔鹽流動回路圖Fig.2 Molten salt flow circuit diagram

1.2 定日鏡場

定日鏡場由2 111個定日鏡組成，其方位和坐標如圖3所示。每個定日鏡寬4 m，高4 m，類型為球面鏡。跟蹤誤差和斜率誤差均為0.001 rad。此外，采用文獻[14]中的多點聚焦瞄準策略，以減少吸熱器上的峰值太陽能流密度。

1.3 熔鹽及管壁物性

吸熱器內傳熱流體采用傳統的太陽鹽（由40%的KNO3和60%的NaNO3組成）。熔鹽物性參數[15]見表2。考慮到下一代吸熱器對高溫、高壓和耐腐蝕性提出了更高需求，采用Haynes 230合金作為吸熱器管壁材料[16]，其性能參數見表3。

圖3 定日鏡場位置坐標圖Fig.3 Heliostat field position coordinate diagram

2 數值方法及模型驗證

表2 熔鹽的物性參數[15]Tab.2 Physical parameters of molten salt

2.1 數值方法

數值計算模型包括光學模型、傳熱模型和應力模型。

在光學計算中，采用MCRT方法準確獲得了全鏡場條件下塔式太陽能吸熱器表面非均勻的能流分布。將吸熱器表面劃分成多個吸熱單元，通過計算吸熱器上每個網格所吸收的太陽能通量來計算吸熱器接收的總太陽能通量。網格單元吸收的太陽能（Qe）由式（1）計算。入射到吸熱器表面的總太陽能（Qi）由式（2）計算：

表3 Haynes 230合金的熱性能和力學性能Tab.3 Thermal and mechanical properties for Haynes 230 alloy

式中：Esunray是每個太陽光束所攜帶的能量，W；nsunray是每個網格單元所接收的太陽光束；Ne是吸收太陽能的網格單元總數。

光學效率定義為吸熱器表面接收的能量與定日鏡場所接收的太陽輻射能量之比，由式（3）計算：

式中：DNI為直接法向輻照度，W·m-2；nh是定日鏡的數量；Lh和Wh分別是每個定日鏡的長度和寬度，m。

傳熱過程采用FVM進行計算。吸熱器表面接收的太陽能部分用于加熱低溫熔鹽，另外一部分能量則通過輻射、對流、導熱等方式散失到外界環境。計算中包含的控制方程如式（4）～（11）所示。

連續性方程：

動量方程：

湍流計算選用標準k-ε湍流模型，近壁面處理采用標準壁面函數，具體描述如下：

k和ε方程：

能量方程：

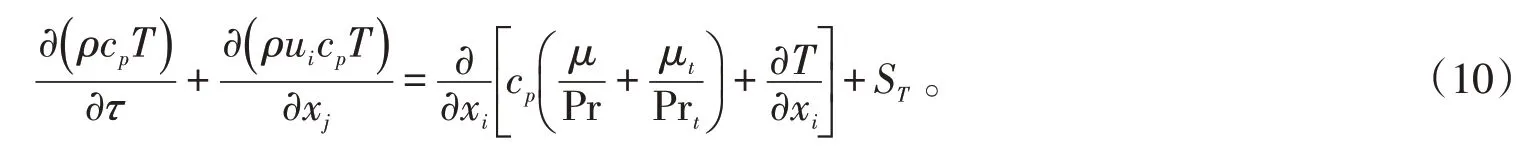
輻射計算采用DO輻射模型，輻射傳遞方程為

式中：μ和μt分別是動力黏度和湍流粘度，Pa·s；σk、σε、C1、C2和Cμ是常數，分別為1.0、1.3、1.44、1.92和0.09；u為速度，m·s-1；ρ為密度，kg·m-3；p為壓力，Pa；cp為工質的定壓比熱容，J·kg-1·K-1；I是輻射強度，W·m-2；和分別是空氣中的位置向量和方向向量。

吸熱器熱效率(ηthe)定義為：

式中：Qi是吸熱器表面的入射太陽能，W；Qr是熔鹽吸收的熱能，W；其中m是熔鹽的質量流量，kg·s-1；h是熔鹽的焓值，kJ·kg-1；下標“1”、“2”、“in”和“out”分別代表流路1、流路2、流路入口和流路出口。

光熱轉換效率(ηot)定義為定日鏡場的光學效率(ηopt)和吸熱器熱效率(ηthe)的乘積，計算公式為

靜態結構模型計算方法是將傳熱模型計算得到的溫度和壓力加載到管道中，利用FEM計算管道的應力和應變。吸熱管被認為是具有各向同性物理特性的熱彈性體。熱彈性的基本方程包括平衡微分方程、應變-位移方程和本構方程。在圓柱坐標系中這些方程表示如下。

平衡微分方程：

根據等效剪切應力定理，忽略體力，可得如下關系：

應變-位移方程：

熱彈性本構方程：

式中：E是楊氏模量，Pa；μ是泊松比；α是熱膨脹系數，K-1；ΔT是溫升，可以從熱流體計算模型中獲得；G表示剪切模量，Pa。

Von Mises理論定義的等效應力公式為

圖4 簡化的面板模型Fig.4 Simplified panel model

以光學模擬得到的太陽能通量作為傳熱模型的熱邊界條件。為了節省計算資源，提高計算速度，基于Christian[10]和Uhlig[11]的研究方法，將管板簡化為矩形板，如圖4所示。平板與實際吸熱器面板相同。矩形面板的橫截面積等于面板中所有管道的橫截面積之和，以保證相同的流速。因此，矩形面板的流體通道等效寬度(We)為12.9 mm。矩形面板的壁厚（t）與管道的壁厚（t）相同，以保持相同的熱傳導。圖5顯示了傳統外露式太陽能吸熱器的換熱模型邊界條件。吸熱器周圍是一個圓柱形空氣區，其直徑比吸熱器大5倍，高度相同。空氣域左側為速度入口邊界。空氣域的其他邊界條件設置為壓力出口。吸熱器面板兩側均視為絕熱薄壁，入口和出口邊界條件分別為質量流入口和壓力出口。外露式吸熱器外壁面接收太陽能輻射，內壁面設置為絕熱。UDF自編程用于計算前一個吸熱器管排的出口溫度，并將其分配給下一個吸熱器管排的入口溫度。計算過程采用二階迎風離散控制方程。

圖5 外露式吸熱器的邊界條件Fig.5 Boundary conditions for cylinder external receiver

在對熔鹽吸熱器進行局部單根吸熱管的熱力計算時，流動換熱計算和上文中簡化管排的邊界條件保持一致。管道半側受熱，將光學計算的該管道處的熱流通過UDF以體熱源的方式加載在受熱壁面。表面對流換熱系數由簡化模型計算得出。入口和出口邊界條件分別為質量流量入口和壓力出口，流動方向參照圖2。質量流量的大小為管排總進口流量的1/32。力學模型的邊界條件定義如下：1）管道外表面與大氣環境接觸，因此外壁面邊界為標準大氣壓0.1 MPa；2）熔鹽在管道中流動時，內壁承受壓力為2 MPa；3）為實現自由膨脹，管道兩端采用弱彈簧邊界條件[17]。

2.2 網格獨立性驗證及模型驗證

選取以下工況為例進行網格獨立性驗證：春分日12時，西風風速1.0 m/s，環境溫度為18℃，熔鹽入口質量流量為45 kg/s，熔鹽入口溫度為573.15 K。流體壁面附近網格的細化y+值均在30左右，滿足標準壁面函數y+值大于15的要求。如圖6所示，當網格數量為691.2萬時，出口溫度Tout和熱效率ηthe的變化趨于穩定。因此，本文選取此網格劃分方法，足以保證計算的準確性。為了驗證本文數值方法的準確性，將模擬結果與美國Solar Two電站的實驗數據進行了對比。對比過程中保持一致的邊界條件。圖7顯示了計算結果與實驗結果之間的比較。可以看出，計算結果與實驗結果吻合較好，最大誤差為1.3%，說明數值模型是可靠的。

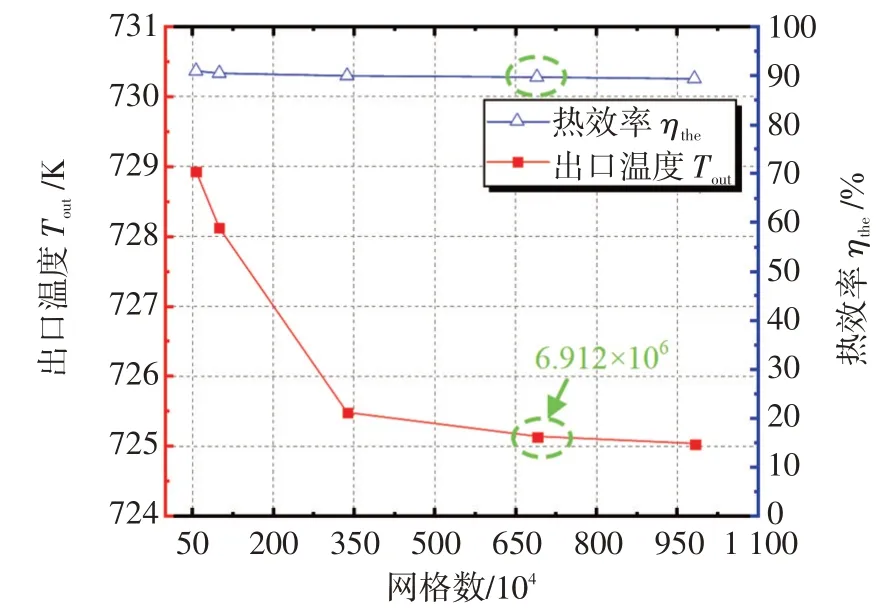
圖6 外露式吸熱器的網格獨立性驗證Fig.6 Grid independence verification for cylinder external receiver

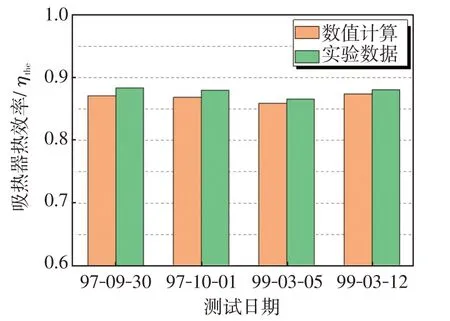
圖7 實驗數據與計算結果之間吸熱器效率比較Fig.7 Comparison of the receiver efficiency between the experimental data and calculated results

3 結果與分析

3.1 太陽能流分布及光學性能

太陽輻射強度與太陽位置隨時間變化而變化，這對吸熱器的性能同樣會產生較大影響。圖8a）、b）、c）分別給出了春分日當地太陽時8：00、12：00、16：00時吸熱器表面能流分布情況。由于北半球的塔式太陽能光熱發電站北側布置更多的定日鏡，因此吸熱器北側的能流密度高于南側。上午8時東西兩側的能流密度表現出明顯的不均勻性，西側的輻照范圍W4～W9遠大于東側的輻照范圍E4～E9。最高能流密度為456.4 kW/m2。正午12時吸熱器東西兩側的入射能量分布基本對稱，最高能流密度達到一天之內的峰值620.3 kW/m2。與上午8時相反，下午16時東側的輻照范圍E4～E9遠大于西側的輻照范圍W4～W9。由此可見隨著太陽方位角和高度角的變化，一天中吸熱器表面太陽能流密度由西側向東側偏移，南北兩側能流密度的分布差異變化較小。

圖8 春分日不同時刻熱流密度分布Fig.8 Distribution of heat flux density at different times on the vernal equinox

圖9展示了外露式吸熱器在春分日不同時刻的光學效率ηopt隨DNI的變化圖。從圖中可以看出，上午光學效率隨著DNI的逐漸增加而增大，正午12時達到最大輻照度，因此光學效率達到最大值。下午光學效率逐漸降低并與上午相同太陽高度時的光學效率保持一致。結果表明，光學效率的變化與DNI的變化具有伴隨性。

3.2 外露式吸熱器的熱性能

本節分析了不同時間和天氣條件下外露式吸熱器光熱轉換性能。

選取春分日西風風速1.0 m/s，熔鹽進口溫度300℃，出口溫度565℃的工況為例進行分析。圖10為晴天條件下，外露式太陽能吸熱器熱效率和光熱轉換效率隨當地太陽時ts的變化。可以看出，一天內外露式吸熱器的熱效率ηthe隨ts先增大后減小，在正午12時達到最大值83%，光熱轉換效率ηot同樣達到峰值58.5%。吸熱器所截獲的太陽能隨著光照強度先增后減，在正午12時達到最大值，由于額定出口溫度保持不變，高熱流密度致使吸熱器內熔鹽質量流量增加，熔鹽與管壁的對流換熱增強，此時吸熱器熱效率達到峰值，光熱轉換效率也隨之達到峰值。

吸熱器外壁面的強制對流同樣對吸熱器換熱性能有著重要影響。圖11所示為外露式吸熱器外壁面對流換熱系數。從整體上看，吸熱器外壁周向對流換熱系數受風向的影響較大。西側屬于迎風側，圖中可以明顯看出西側管壁的對流換熱系數大于東側（背風側）管壁。同時，由于低溫熔鹽從北側近入，吸收高溫熱流后從南側流出，所以吸熱器北側管壁溫度較低，南側管壁溫度偏高，故南側比北側具有較高的對流損失。

圖12展示了春分日正午12時吸熱器熱效率和光熱轉換效率隨風速的變化。當西風風速由1 m/s增加到20 m/s時，吸熱器的熱效率ηthe由83%降低至71%，光熱轉換效率ηot由58.4%降低至50%。并且隨著風速逐漸增大，熱效率降幅更加顯著。這是由于外露式吸熱器的暴露面積較大，在較大風速下產生了較高的對流損失。

圖13為春分日正午12時外露式吸熱器外壁面的溫度分布云圖。Y軸的正方向為正北，X軸的正方向為正東。在吸熱器的周向上，南側管排的溫度明顯高于北側管排，且峰值溫度為890.96 K，出現在最南側管排上。可見溫度也表現出強烈的非均勻性，且與圖8b）所示的表面熱流密度分布恰好相反。出現這種現象的原因可歸結于吸熱器熔鹽的流動布置方式。在此布置方式下，熔鹽從最北側高熱流密度區進入，由于低溫熔鹽和高熱流密度的壁面溫差較大，換熱能力較強。在由北向南流動的過程中，熔鹽吸熱，溫度逐漸升高，而管壁太陽能流密度逐漸降低，換熱逐漸趨于緩慢，吸熱管壁溫度與熔鹽溫度變化趨勢一致。在北側入口附近，由于低溫熔鹽從高熱流密度區進入，避免了該區域峰值溫度過高；在南側出口附近，由于南側太陽能流密度較小，熔鹽溫度較高，甚至會出現熔鹽向外放熱的現象。這些現象能夠在一定程度上降低吸熱管壁的最高溫度，提高吸熱器的安全性能。

圖9 外露式吸熱器春分日不同時刻的光學效率和DNIFig.9 Optical Efficiency and DNI of cylinder external receiver at different times of the spring equinox

圖10 外露式吸熱器春分日不同時刻的熱效率和光熱轉換效率Fig.10 Thermal efficiency and photothermal conversion efficiency of cylinder external receiver at different times of spring equinox

圖11 外露式吸熱器春分日12時外壁周向對流換熱系數Fig.11 Circular convective heat transfer coefficient of outer wall of cylinder external receiver at 12:00 on spring equinox

圖12 外露式吸熱器不同風速的熱效率和光熱轉換效率Fig.12 Thermal efficiency and system photothermal conversion efficiency of cylinder external receiver at different wind speeds

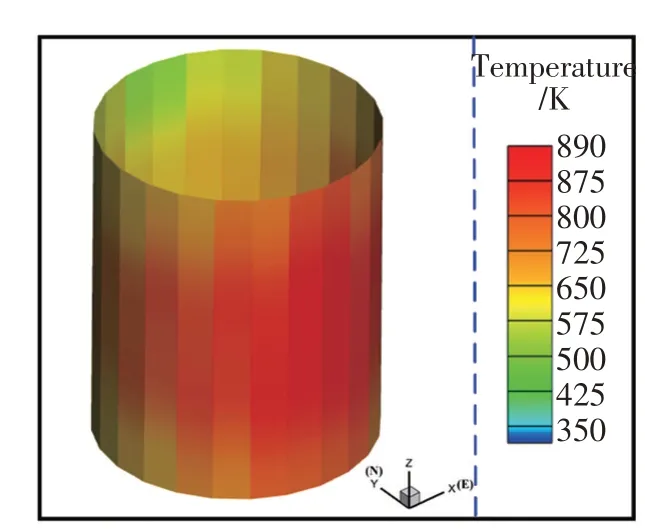
圖13 外露式吸熱器溫度分布云圖,春分日正午12時，Tmax=890.96 KFig.13 Cloud chart of temperature distribution of cylinder external receiver at 12 noon on the spring equinox,Tmax=890.96 K

3.3 外露式吸熱器的應力分析

上文中已經獲得了典型工況下熔鹽吸熱器的太陽能流密度，以及整體和局部的溫度分布，發現不均勻的能流分布是造成溫度分布不均的主要原因。溫度分布不均和局部熱點，給吸熱器結構和壽命帶了較大的安全隱患。因此本節針對吸熱器在典型工況真實能流分布下的整體及局部的應力特性進行了探討。

圖14為吸熱管的溫度分布和綜合應力分布。如圖所示，綜合應力沿軸向分布與溫度分布趨勢相同，在管道中部達到峰值。在圓周方向看，高能流密度區吸熱壁面的熱應力也高于低能流密度區吸熱壁面，但峰值位于吸熱器高能流密度區與低能流密度區交界處，這是因為此位置的溫度梯度最大，應力集中明顯。這一點可以從圖15管道的中間截面處更清楚地看出。

圖14吸熱管溫度分布和應力分布，管排E8，管道241Fig.14 Temperature distribution and stress distribution of heat absorber tube,panel E8,tube 241

圖15 為吸熱管中間截面的綜合應力、壓應力、熱應力分布云圖。從圖中可以清楚地看出，溫度梯度導致的熱應力與操作壓力導致的壓應力在數量級上是一致的，但在分布上有很大的不同。壓應力在吸熱器管道內壁面達到峰值，并由內壁面向外壁面沿徑向逐漸減小；而熱應力峰值出現兩側中間偏下區域。綜合應力是由溫度梯度和壓力共同造成的，其分布是熱應力和壓應力分布的綜合體現。

圖15 吸熱管E8-241中間截面（Z=3.1 m）的綜合應力、壓應力、熱應力分布Fig.15 Distribution of comprehensive stress,compressive stress and thermal stress in the middle section（Z=3.1 m）of heat absorber tube E8-241

圖16展示了各個吸熱管排中間管道的最大綜合應力，通過此圖來分析整個吸熱器的應力分布。可以看出綜合應力的變化趨勢與熱流分布完全一致，高能流密度區的吸熱壁面熱應力遠高于低能流密度區吸熱壁面。產生這種現象的根本原因在于壁面溫差，正午12時管排E1～E6和W1～W6表面熱流密度高，但熔鹽溫度較低，因此內外壁面溫差大，產生較大的綜合應力。從選取的單管來看，峰值應力52.48 MPa正是出現在管排E1中間管道上，管排E1能流密度及壁面溫差最大。最低應力28.87 MPa在管排E12處中間管道上，管排E12能流密度及壁面溫差均為最小。峰值應力與最小應力相差近2倍。由此可以看出，即使在多點聚焦瞄準策略下吸熱管外側熱流分布相對均勻，但吸熱管內外側受熱不均的問題仍然存在，受光側和背光側較大溫差仍會產生較大的局部應力。未來的研究應著重解決外露式吸熱器單側受熱問題。

圖16 每個管排中間管道的最大綜合應力Fig.16 Maximum equivalent stress of the middle pipe of each panel

4 結語

本文結合MCRT、FVM、FEM建立了基于傳統的外露式太陽能吸熱器全尺寸的光-熱-力耦合數值模型，探討了不同日期和非均勻太陽能流分布對吸熱器熱性能的影響，并進一步分析了多點聚焦瞄準策略下單側受熱吸熱器的熱應力特性。得出以下主要結論：

1）隨著太陽高度的變化，吸熱器一天中集中熱流密度由西部向東部偏移，南北兩側熱流密度的差異變化較小。光學效率的變化與DNI的變化具有伴隨性。

2）正午時刻的高熱流密度致使吸熱器內部流體傳熱增強，因此吸熱器熱效率和光熱轉換效率均達到最大值。吸熱器效率受風速影響較大，且迎風側對流換熱系數較大，帶來較高的熱損失。

3）吸熱管壁中間溫度較高，進出口位置溫度較低，并且由于單側受熱，受光側和背光側溫差較大，交界處產生較大的集中應力。管壁的綜合應力由熱應力占主導。

4）全尺寸吸熱器綜合應力的變化趨勢與熱流分布基本一致，高能流密度區的吸熱壁面熱應力遠高于低能流密度區吸熱壁面。峰值應力與最小應力相差近2倍。由此可以看出，即使在多點聚焦瞄準策略下吸熱管外側熱流分布相對均勻，傳統的外露式吸熱器由于單側受熱仍會產生較大局部應力。