二面角的平面角的求法面面觀
張 平
(廣東省珠海市實驗中學)
二面角的平面角是立體幾何中的一個核心概念,也是高考的重點考查目標.因此厘清如何求解二面角的平面角,明晰求解二面角平面角的常用途徑與方法便顯得尤為重要.本文在歸納總結二面角的平面角問題求解的主要方法與解題步驟的基礎上,結合一道相關試題對每種方法進行了具體分析應用,以期在豐富與完善讀者解決此類問題的方法的同時,培養結合題目條件靈活選擇方法的意識,提升解決問題的能力.
1 二面角平面角的定義
從一條直線出發的兩個半平面所組成的圖形叫做二面角,這條直線叫二面角的棱,這兩個半平面叫做二面角的面.在二面角的棱上任取一點O,以點O為垂足,分別在兩個半平面內作垂直于棱的射線OA,OB,則射線OA,OB構成的角∠AOB叫做二面角的平面角.根據二面角平面角的定義知∠AOB∈[0,π].
2 二面角平面角的常用求法
2.1 射影面積法
已知平面α內的平面圖形Γ的面積為S,它在平面β內的射影Γ′的面積為S′,設平面α與平面β所成二面角的平面角為θ,則當時,當時,cosθ=

圖1
2.2 幾何法
1)定義法
用定義法求解二面角平面角的基本步驟為“一找、二算、三得出結論”,首先,結合已知條件及線面垂直關系,作出二面角的平面角,如圖1中的∠CED;其次,利用直角三角形計算求解,即求∠CED的三角函數值或角度;最后,根據題目要求得出結論.
2)距離法
由圖1知在Rt△DEC中,sin∠CED=,進而問題轉化為分別求平面α內一點C到平面β的距離與到棱l的距離即可.
2.3 坐標法(法向量法)
設平面α與平面β所成二面角的平面角為θ,平面α與平面β的法向量分別為m,n,則|cosθ|=|cos〈m,n〉|,若θ∈[0],則cosθ=|cos〈m,n〉|;若θ∈,π],則cosθ=-|cos〈m,n〉|.坐標法求解二面角的一般步驟:首先,根據題目條件建立適當的空間直角坐標系,并準確表示相關點的坐標;其次,求出兩個平面的法向量,并計算兩個法向量夾角的余弦值;最后,結合圖形及題目要求得出結論.
2.4 向量法(空間向量法)

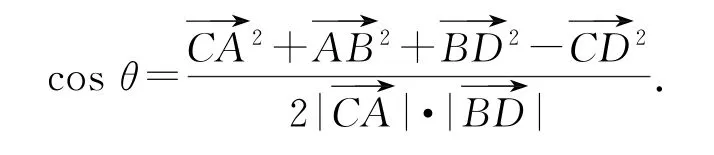
根據此公式知要求二面角平面角的余弦值,只需在兩個半平面內分別“找出”不在棱上的一點,如圖2中的點C,D,再分別求出CD,以及點C,D到棱l的距離AC,BD及棱l上兩垂足間的距離AB即可.

圖2
3 應用舉例
題目如圖3所示,在四棱錐P-ABCD中,底面ABCD是邊長為2的正方形,PD=PA=,PC=3.

圖3
(1)證明:平面PAD⊥平面ABCD;
(2)求二面角B-PD-A的余弦值.
分析第(1)問較為簡單,證明過程略.本文用上述方法重點求解第(2)問.
解法1射影面積法

解法2定義法
由解法1 知AB⊥平面PAD,則AB⊥PD.如 圖4所示,過點A作AM⊥PD于M,連 接BM,則AB⊥AM.易證PD⊥平面MAB,從而PD⊥BM,則∠AMB為二面角B-PD-A的平面角.在△PAD中,PD=PA=,AD=2,所以S△APD=2,AM=,在Rt△BAM中,有

圖4

解法3距離法
由解法1 知AB⊥平面PAD,則點B到平面PAD的距離AB=2,由解法2知BM⊥PD于M,且BM=,結合圖形知二面角B-PD-A為銳二面角,設二面角B-PD-A的平面角為θ,則

點評解法1~解法3主要是從幾何的角度進行求解,而前提是挖掘了“AB⊥平面PAD”這一關鍵信息,但對這一信息如何使用,有不同的思考與選擇.不同的使用方式導致解題方法的區別,體現思維的發散性.
解法4坐標法


圖5
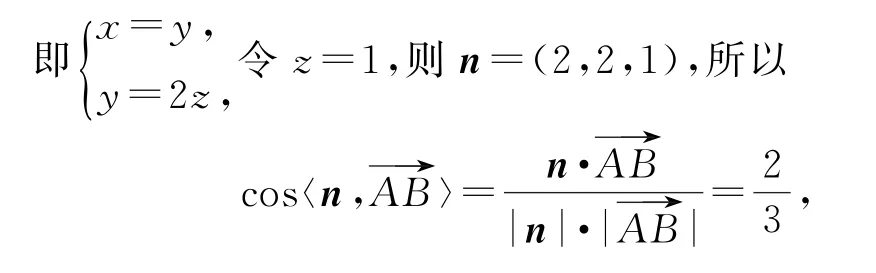
結合圖形知二面角B-PD-A為銳二面角,則二面角B-PD-A的余弦值為.
點評解法4 是利用坐標法進行求解,首先是將“平面PAD⊥平面ABCD”轉化為線面垂直關系,實現建立空間直角坐標系的基本要求,其次是坐標原點與坐標軸的選擇,要便于點的坐標表示.其好處在于將幾何問題“代數化”,“弱化”了對空間想象能力的考查.
解法5空間向量法

解法6空間向量法
如圖6 所示,在△PAD中,過點A作AM⊥PD于M,由解法2可 知AM=,在Rt△PAM中,有
圖6


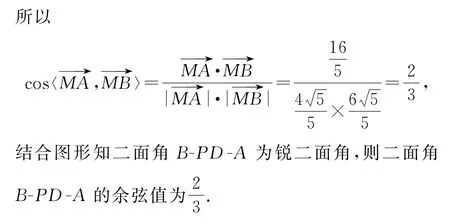
點評解法5~解法7均是利用空間向量法進行求解,雖側重點有所不同,但均是以“在兩個半平面內找與棱垂直的向量”為中心,借助平面向量基本定理、空間向量基本定理及相關運算性質求解.解法5結合坐標法進行運算,簡捷快速,解法6與解法7則凸顯向量運算性質的應用.
求解二面角的平面角方法眾多,首先,要理解掌握常用的求解方法與策略,其次,要具體問題具體分析,通過對題目條件的深入分析、思考與挖掘,找到已知信息與求解方法之間聯系的橋梁.同時結合圖形特點確定最優求解路徑,使用最便捷的方法,快速求解,在提升解題能力的同時完善與發展數學學科素養.
(完)

