例析幾何體外接球問(wèn)題

孫朝鵬

(云南省曲靖市會(huì)澤縣第一中學(xué)校)

對(duì)近10年的高考數(shù)學(xué)試題進(jìn)行分析,不難發(fā)現(xiàn)與立體幾何相關(guān)的問(wèn)題常常會(huì)出現(xiàn)球的身影,但對(duì)于學(xué)生而言幾何體的外接球和內(nèi)切球問(wèn)題具有一定的難度.求解幾何體的外接球問(wèn)題關(guān)鍵在于確定球心位置及球體半徑,根據(jù)幾何體的空間結(jié)構(gòu)特點(diǎn)可以分為不同的外接球模型.本文主要介紹四種不同的三棱錐外接球模型,給學(xué)生提供更多幾何體外接球問(wèn)題的求解思路,以便于學(xué)習(xí)和參考.

1 墻角模型

墻角模型具體是指問(wèn)題中三棱錐的三條棱滿足兩兩互相垂直條件,求解時(shí)可將其補(bǔ)形為長(zhǎng)方體(或正方體),進(jìn)一步按照長(zhǎng)方體(或正方體)的外接球思路求解.墻角模型是根據(jù)補(bǔ)形后的幾何體結(jié)構(gòu)特點(diǎn)形似墻角而命名.

例1在正三棱錐S-ABC中,M,E分別是棱SC,BC的中點(diǎn),且AM⊥ME,若側(cè)棱SA＝2,則正三棱錐S-ABC外接球的表面積為_(kāi)________.

解析如圖1所示,取AB,BC的中點(diǎn)D,E,連接AE,CD,AE,CD交于點(diǎn)H,連接SH,則點(diǎn)H是底面正△ABC的垂心,所以SH⊥平面ABC,SH⊥AB.

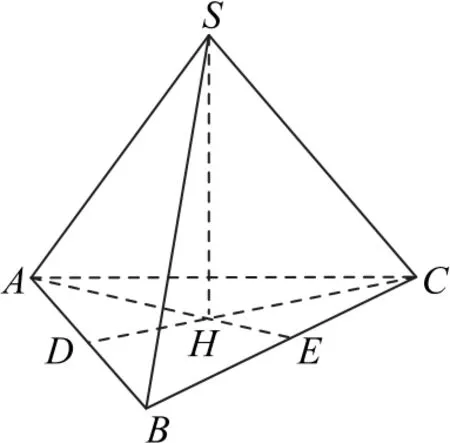
圖1

又CD⊥AB,SH∩CD＝H,所 以AB⊥平 面SCD,所以AB⊥SC.同理,BC⊥SA,AC⊥SB,即正三棱錐對(duì)棱互相垂直.

如圖2 所 示,因 為AM⊥ME,SB∥ME,所 以AM⊥SB.因?yàn)锳C⊥SB,AM∩AC＝A,所以SB⊥平面SAC,SB⊥SA,SB⊥SC,而SA⊥BC,SB∩BC＝B,所以SA⊥平面SBC,即SA⊥SC,故三棱錐側(cè)棱兩兩垂直.

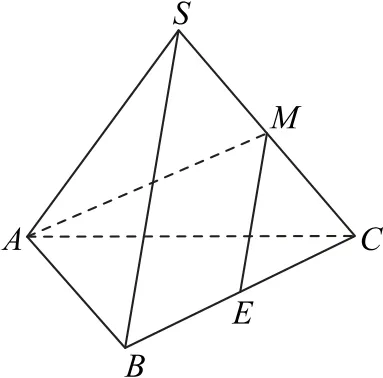
圖2

令三棱錐S-ABC的外接球半徑為R,如圖3 所示,可知正方體的邊長(zhǎng) 為SA＝SB＝SC＝,則,即R2＝9,S＝4πR2＝36π,故三棱錐S-ABC外接球的表面積為36.

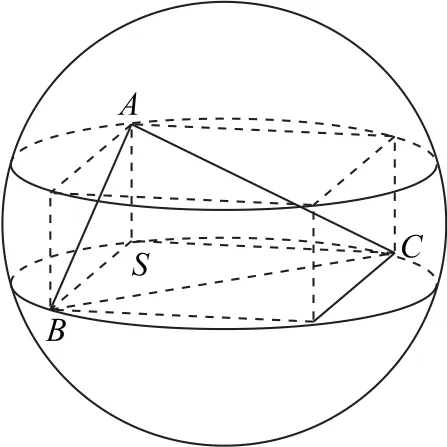
圖3

2 對(duì)棱相等模型

對(duì)棱相等模型實(shí)質(zhì)上是指三組異面棱長(zhǎng)相等的三棱錐,可借助這三組棱長(zhǎng)求解外接球半徑.常見(jiàn)的求解步驟如下:

1)根據(jù)問(wèn)題已知條件,找到三組不在同一平面卻相等的棱長(zhǎng),分別求出對(duì)應(yīng)的長(zhǎng)度x,y,z;

2)根據(jù)勾股定理和墻角模型中的公式2R＝(a,b,c分別為長(zhǎng)方體的長(zhǎng)、寬、高),將其轉(zhuǎn)化為與棱長(zhǎng)x,y,z有關(guān)的等式;

3)憑借推導(dǎo)得到R2＝,將棱長(zhǎng)代入求得外接球半徑.

例2如圖4所示,在三棱錐A-BCD中,AB＝CD＝2,AD＝BC＝3,AC＝BD＝4,則三棱錐A-BCD外接球的表面積為_(kāi)________.

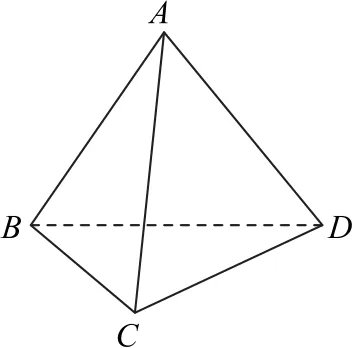
圖4

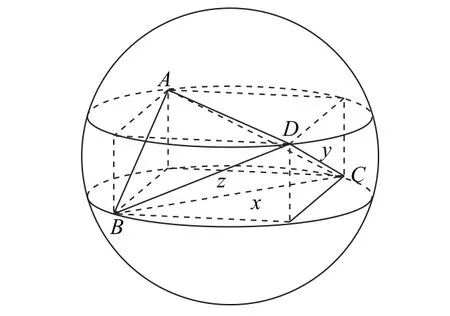
圖5

3 垂面模型

垂面模型主要是指錐體有關(guān)平面與底面垂直,則此時(shí)錐體外接球的球心一定在該平面上,球心的投影為底面外接圓的圓心,根據(jù)這些幾何關(guān)系尋找等價(jià)關(guān)系式,即可求出錐體外接球的半徑.應(yīng)用垂面模型解答錐體的外接球問(wèn)題,常見(jiàn)求解步驟如下:

1)在錐體中找到與底面垂直的平面,判斷錐體外接球球心O的位置;

2)求解底面圖形的外接圓圓心O1與半徑r;

3)由于OO1,r,R構(gòu)成直角三角形,根據(jù)勾股定理求出R的大小,即可知錐體外接球的半徑及其他值的大小.

例3一個(gè)幾何體的三視圖如圖6所示,則該幾何體的外接球表面積為( ).

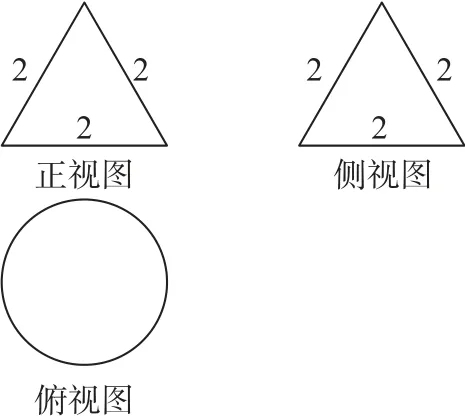
圖6

A.3π B.2π

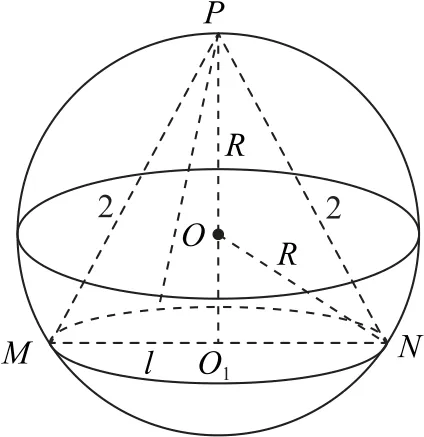
圖7

立體幾何是高中數(shù)學(xué)重要的內(nèi)容,幾何體的外接球問(wèn)題是立體幾何中常見(jiàn)的問(wèn)題.解答有關(guān)幾何體的外接球問(wèn)題時(shí),可以嘗試運(yùn)用上述模型進(jìn)行解答.全面掌握立體幾何外接球模型有助于高效解答問(wèn)題,從而提升解題效率.學(xué)習(xí)、理解并運(yùn)用這些不同的外接球模型解答相關(guān)問(wèn)題,也是高中數(shù)學(xué)的重要學(xué)習(xí)內(nèi)容之一.

鏈接練習(xí)

1.正三棱錐A-BCD內(nèi)接于球O,且底面邊長(zhǎng)為3,側(cè)棱長(zhǎng)為2,則球O的表面積為_(kāi)________.

2.一個(gè)六棱柱的底面是正六邊形,其側(cè)棱垂直底面.已知該六棱柱的頂點(diǎn)都在同一個(gè)球面上,且該六棱柱的體積為,底面周長(zhǎng)為3,則這個(gè)球的體積為_(kāi)_______.

3.若長(zhǎng)方體外接球體積為36π,則該長(zhǎng)方體的表面積最大為_(kāi)_______.

4.已知等邊△ABC的邊長(zhǎng)4,且M,N分別為AB,AC的中點(diǎn),沿著MN將△ABC折成直二面角,則四棱錐A-MNCB外接球的表面積為_(kāi)________.

鏈接練習(xí)參考答案

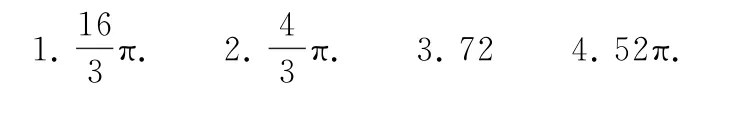
(完)