X波段雙偏振氣象雷達差分相位質量控制

徐 星， 閆 賀， 周 曄， 汪 玲， 孫小航， 李益兵， 朱岱寅

(1.南京航空航天大學電子信息工程學院雷達成像與微波光子技術教育部重點實驗室， 江蘇南京 211106； 2.中國航空工業集團公司雷華電子技術研究所， 江蘇無錫 214000； 3. 南京恒電電子有限公司， 江蘇南京 211106)

0 引 言

X波段雙偏振雷達由于其價格低、天線體積小、空間分辨率高等優點受到了氣象雷達研究學者的廣泛關注[1-2]。與傳統的單極化雷達相比，雙極化雷達不僅可以測量得到水平反射率因子Zhh，還可以通過發射和接收水平,豎直兩種電磁波，從而得到差分反射率Zdr，總差分相位Ψdp和差分相移率Kdp[3-5]。其中差分相移率在傳播路徑上存在優異的性能：Kdp僅僅與介電常數、密度以及空氣中降水粒子的形態有關，在傳播路徑上受到波束阻擋以及降水粒子衰減的影響較小，且對雨滴譜的變化不敏感[6]。因此對于氣象參數的應用也主要依賴于差分相移率的值。

通常情況下，根據雷達回波直接得到的總差分相位Ψdp是由兩部分組成：后向差分相位δdp和前向散射引起的差分相位Φdp。其中，差分傳播相移率Kdp是前向散射引起的差分相位Φdp在徑向距離上的斜率。后向差分相位δdp與降水粒子的散射特性相關。若雷達傳播路徑中降水粒子滿足瑞利散射條件，則可以忽略δdp的值，但隨著降水量的增加，降水粒子的直徑不斷增加，后向差分相位δdp也會隨之增加。一般認為達到中雨時，降水區不再滿足瑞利散射條件，此時δdp的值不可忽略。后向差分相位可以作為一個單獨的氣象雷達觀測值，也具有很多的應用，可以用于降水微物理量的檢測以及操作雷達的校準。

在探究測量得到差分相位的準確性中，很多國內外學者都提出不同的方法。常見的是采用濾波的方式對差分相位進行處理。Hubbert等提出了采用無線沖激響應和有限沖激響應[7]對實測差分相位值進行處理。何宇翔通過研究總差分相位Ψdp的特點，將卡爾曼濾波[8]的方法加入到數據的處理當中。HU等人提出運用小波分析[9]的方法來對測量得到的總差分相位進行處理。但上述的處理方法僅依賴于單一徑向上差分相位的變化特點，在實際降雨區的測量過程中，相鄰徑向上差分相位的值存在一定的聯系。本文將結合測量得到的總差分相位在PPI(Plan Position Indicator)圖中呈現的特點進行濾波處理。去除電磁波傳播路徑上其他電磁波的干擾，并利用后向差分相位與差分反射率之間的關系，通過構建新的矩陣，充分利用徑向差分相位變化的特點，從而得到差分相移率，重構前向散射引起的差分相位，實現對前向散射相位和后向差分相位的分離。

1 雙極化雷達參數和數據

為驗證本文提出方法的有效性，將選取代爾夫特理工大學的雙偏振X波段國際通信和雷達研究中心(International Research Centre for Telecommunications and Radar,IRCTR)的數據說明差分相位質量控制的情況。這是一種X波段的小雨雷達(IRCTR Drizzle Radar,IDRA)[10-11]。該氣象雷達的天線每一分鐘轉一圈，即每分鐘掃描360°，天線的輻射角度約為0.05 rad，每個徑向的輻射距離都為15 330 m， 將每一條射線的徑向輻射范圍分為512個距離庫，則每個距離庫的長度為30 m。雷達的主要參數值如表1所示。圖1為2009年5月23日20時33分雷達實測得到的總差分相位Ψdp,等效反射率因子Zhh和差分反射率因子Zdr的PPI圖。

表1 IDRA雙極化雷達參數表

(a) 總差分相位Ψdp

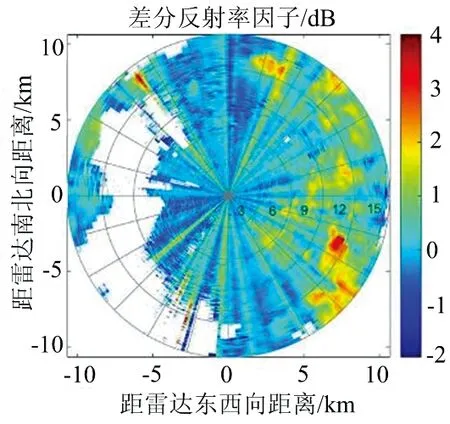
(b) 差分反射率因子Zdr

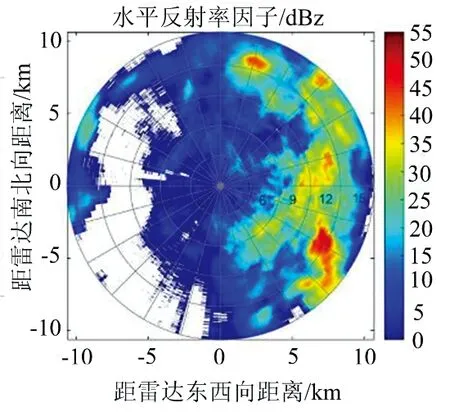
(c) 水平反射率因子Zhh圖1 2009-05-23T20：33：00雷達實測數據PPI圖

此時天線的俯仰角為0.008 7°。雷達的發射信號在9.475 Hz的中心頻率周圍以5 MHz的帶寬進行線性調制。雷達測得的數據以NetCDF格式存儲。

2 差分相位的預處理

通過氣象雷達接收所發射電磁波的回波，可以得到對氣象類型和氣象情況判別的基本物理量。但在實際情況中，大氣環境多變復雜，外界電磁波對雷達系統的干擾會造成雷達回波異常，從而嚴重影響測量數據的質量并對后續的數據應用產生干擾。電磁波的干擾造成的數據異常在PPI的顯示端主要有三種表現：麻點狀雜波、數據的突出雜點和條幅狀的異常區域。干擾的來源主要有兩種：

1) 在接收回波時，會受到非降水回波的干擾，包括外界頻率源的干擾和較遠距離上一定帶寬的干擾源。

2) 氣象雷達探測的遠端某個方向上存在固定的單頻點噪聲。

氣象雷達的每個徑向方位角之間有一定的間隔，構成了360°的PPI數據。如圖2所示為沿雙極化雷達某一射線方向的工作示意圖。

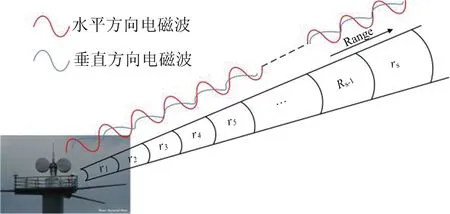
圖2 雙極化雷達工作示意圖

2.1 消除非氣象回波數據點

認為差分相位的PPI圖中麻點狀雜波和突出的雜點主要來源是非氣象回波，以滑動數據窗口格來進行處理，以每個要處理的距離單元為中心點，建立一個(2m+1)×(2n+1)大小的滑動窗口，其中i表示為方位向距離庫順序，j表示為徑向距離庫順序。

1) 對于某些區域內為非降水地區，即這些區域的距離單元內差分相位沒有值，但由于回波的影響，使得該距離單元產生了數據，可能會導致降水區域的誤判。計算滑動窗口內有效距離單元個數占總滑動窗口距離單元個數的百分比，當占比率小于設定閾值γ時，則認為該滑動窗口中心距離單元為無效數據點而進行去除，即

(1)

式中，Ψdp(i,j)為雙極化雷達測量所得數據給定距離庫點(i,j)的總差分相位值，Pi,j為選定滑動窗口內有效距離單元個數占總距離單元個數的百分比，NaN表示距離單元內的無效數據。為了保證處理之后回波數據的真實性，還需要注意當前距離單元內數據的移除不影響下一次窗口內的數據，且不受上一次剔除數據的影響。

(2)

則每個窗口格中可以得到(2m+1)×(2n+1)-1個ΔΨdp的值。記錄下滑動窗口格內ΔΨdp大于設定閾值β1的個數μ，并計算：

(3)

若α的值超過設定的閾值β2，則判定該數據點為突出雜點，需要對該數據點進行剔除。

由于該距離單元內本身就存在氣象回波數據，因此需要對剔除后的距離單元進行插值處理，使得該距離單元內的數據滿足徑向上差分相位的變化規律。在該距離單元為中心的滑動窗口內，對窗口中其他距離單元數據進行均值處理，處理得到的數據作為該距離單元的插入值。圖3顯示了數據處理前后差分相位的PPI圖。其中，紅色框內顯示的是無效數據點處理的情況，對比圖3(a)和(b),可以看出無效數據可以有效的被去除。圖3(b)中的黃色框內顯示的是非氣象回波造成的突出雜點，可以明顯看到同一徑向上相位值的突變情況，造成徑向上差分相位值的波動。從圖3(c)中可以看到，通過上述處理，同一徑向上的差分相位數據的質量得到很好的控制。

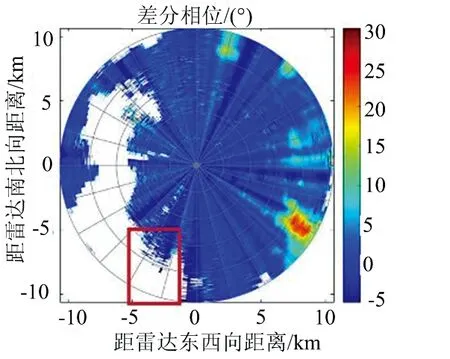
(a) 實測總差分相位Ψdp

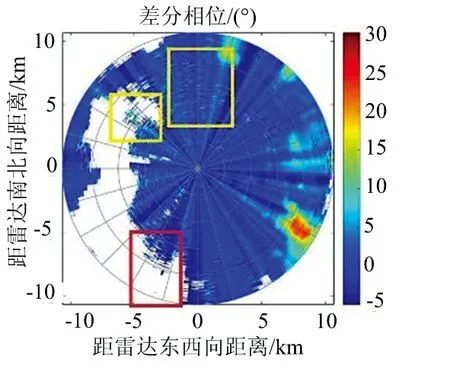
(b) 去除非降水數據后差分相位

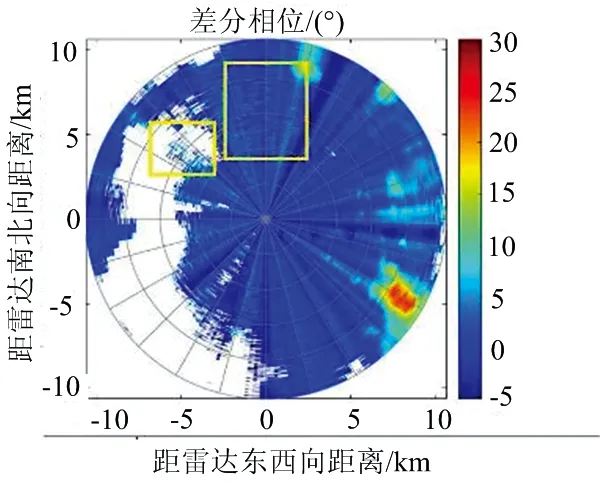
(c) 去除非氣象回波后差分相位圖3 去除非氣象回波數據前后差分相位PPI圖

2.2 條幅狀雜波的去除

由于雷達在某一方位向接收回波時，可能會受到該方位向上單頻點的電磁干擾，造成測量得到的某些相鄰徑向上數據出現與周圍環境不匹配的情況。這種大規模的數據誤差，可以通過構造特征參量來檢測方位向上和距離向上的連續性，定位誤差數據所在的位置。

設定相鄰徑向上差分相位的差為ΔΨdp=|Ψdp(i)-Ψdp(i-1)|，其中，i表示方位上的位置，Ψdp為總差分相位的值。由于在每個方位向距離庫上，存在多個距離單元個數，因此，記錄下ΔΨdp中大于θ1的個數，記為Nth。記Nth1為第i行和第i-1行之間的差分相位值大于θ1的個數，Nth2為第i行和第i+1行之間的個數。設定參數ΔNth=|Nth1-Nth2|，若ΔNth大于某一設定參數θ2時，則判定該徑向上的數據存在誤差。

在確定條幅狀干擾回波的具體位置之后，將該條幅狀干擾回波全部去除，再采用插值法保證數據的準確性。條幅狀雜波的出現往往會伴隨著多條徑向出現問題。在對條幅狀雜波位置進行判斷時，是對每個徑向的數據進行遍歷，因此利用相鄰徑向差分相位大于設定閾值的距離庫個數差，可以有效地定位條幅狀雜波開始和結束的位置。首先將條幅狀雜波所在所有的徑向數據進行去除，再從相鄰徑向同一距離庫上正常的回波數據徑向差值進行填補，恢復真實回波數據值。設定條幅狀干擾回波共有n條徑向，k為這一干擾回波中所有方位之間的某一個方位，則處理之后的差分相位值為

(4)

去除雜波條幅狀雜波前后的差分相位PPI對比結果如圖4所示。圖4(a)為去除非氣象回波后的差分相位結果，此時未進行條幅狀雜波的去除，可以看出橙色框內的數據存在明顯的誤差，對整個徑向上的數據都造成了影響。通過定位該徑向的位置并進行數據處理之后，其結果如圖4(b)所示，方位向差分相位的變化符合實際情況。

3 分離后向差分相位

(a) 去除非氣象回波后差分相位

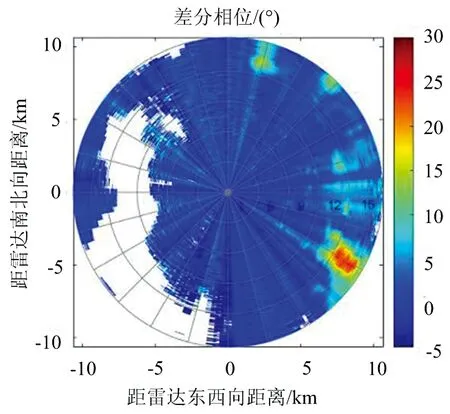
(b) 去除條幅狀雜波后差分相位圖4 去除條幅狀雜波前后差分相位PPI圖

對于波長較長的雷達，在計算前向散射引起的差分相位時，常常忽略掉后向差分相位的值。隨著雷達頻率的增大，非瑞利散射效應無法忽略，因此需要對后向差分相位進行去除。本文主要通過計算差分相移率，重構前向差分相位，達到了對后向差分相位去除的目的。

3.1 理論分析

雷達直接測量得到的總差分相位，后向差分相位以及前向散射引起的差分相位之間存在簡單的和式關系[12]：

Ψdp=Φdp+δdp

(5)

其中，后向差分相位δdp與差分反射率因子Zdr之間存在很好的相互關聯，因此可以通過測量差分反射率的值來估計后向差分相位。δdp和Zdr這兩個參數都不受到射線傳播效應的影響。δdp和Zdr之間的關系可以表示為

(6)

參數a0,a1和a2都是多項式回歸系數。假定某一徑向距離上的兩個距離庫分別表示為ra和rb(rb>ra)，兩距離庫上的差分反射率因子分別為Zdr(ra)和Zdr(rb)。若存在Zdr(ra)=Zdr(rb)，則有ΔΨdp=Ψdp(rb)-Ψdp(ra)=ΔΦdp，即可以認為兩距離庫上差分反射率相同時，差分相位的插值可以認為等于前向差分相位的插值。但在實際的測量中，由于在差分反射率相等的兩距離庫范圍內降水的微物理量以及雷達測量過程中的統計變化，差分相位之間可能選在擾動干擾，即ΔΨdp=ΔΦdp+ε，ε即為擾動的誤差值。為了彌補這些測量中可能存在的缺陷，設定當一條雷達射線上測量得到的兩個距離庫上的每個差分反射率差組合|Zdr(rb)-Zdr(ra)|小于某一設定的值λ時，即認為此時的ΔΨdp=ΔΦdp。

設定某一條雷達射線上測量所得到的數據矢量差分反射率因子Zdr和差分相位Ψdp分別為

Zdr=[Zdr(r1),Zdr(r2)，…，Zdr(rN)]TΨdp=[Ψdp(r1),Ψdp(r2),…,Ψdp(rN)]T

(7)

式中T表示轉置，N表示雷達射線上距離庫上的總距離庫數。對于本文所用的IDRA數據中N值為512。本文主要利用相同差分反射率的距離庫上可以用總差分相位差估計前向差分相位來計算差分相移率的特點，需要知道同一徑向上不同距離庫之間的差值特點，因此構建了兩個矩陣A和B。

(8)

(9)

矩陣B的第i行即為值b的二進制表示方式(左邊為低位)。例如：

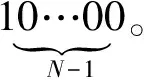
(10)

通過使用矩陣A，可以計算一條雷達射線上每兩個不同距離庫之間的差分反射率因子和差分相位之間的差值：

ΔZdr=A·ZdrΔΨdp=A·Ψdp

(11)

w=B′diag[(ζhh)d]diag[10(-e·Zdr)]Zhh=10log10(ζhh)

(12)

式中，Zhh的單位為dBz，ζhh的單位為mm6m-3。參數d,e是根據降雨偏振分量測量的自適應性得到的。對加權系數w的每一行進行歸一化，即

(13)

接著，將得到的差分相位差矩陣ΔΦdp中的元素沿著距離向進行分配。

(14)

式中Δr為同一徑向上相鄰距離單元之間的距離。因此可以得到單向差分相移的值為

(15)

通過構建評估系數σKdp來檢驗計算所得到的Kdp[13]的準確性。

(16)

理論情況下，在雷達的徑向范圍內，若該區域存在降水區，則前向散射引起的差分相位值會增加，即該距離單元內存在差分相移率的值。若某區域內無降水現象，則前向散射引起的差分相位的值將保持不變，此時距離單元內不存在差分相移率。因此，在對前向散射引起的差分相位進行重構時，只需要關注存在降水區域的差分相位就可以。

3.2 個例分析

為了驗證后向差分相位和前向散射引起的差分相位的值，我們將提出的方法應用于上文提出的位于荷蘭213 m高的氣象塔頂部的偏振X波段雷達IDRA的數據集。由于后向差分相位和差分反射率之間的關系(式(6))在Zdr大于0 dBz的情況下成立，因此，在實驗過程中排除了反射率低于0 dBz且線性退極化比大于-15 dBz的距離庫，這種處理方式也確保了氣象散射體的存在。結合表1中X波段雙極化雷達的數據情況以及雨滴譜的特點，對于去除后向散射相位數據處理過程中需要用到的參數選擇為：λ=0.3 dBz,d=0.68,e=0.042。通過計算得到差分相移率，并通過差分相移率重構得到前向散射導致的差分相位[14]。利用實測數據得到的總差分相位值，計算得到了后向差分相位值。圖5為計算所得氣象數據的PPI圖。

(a) 差分相移率Kdp

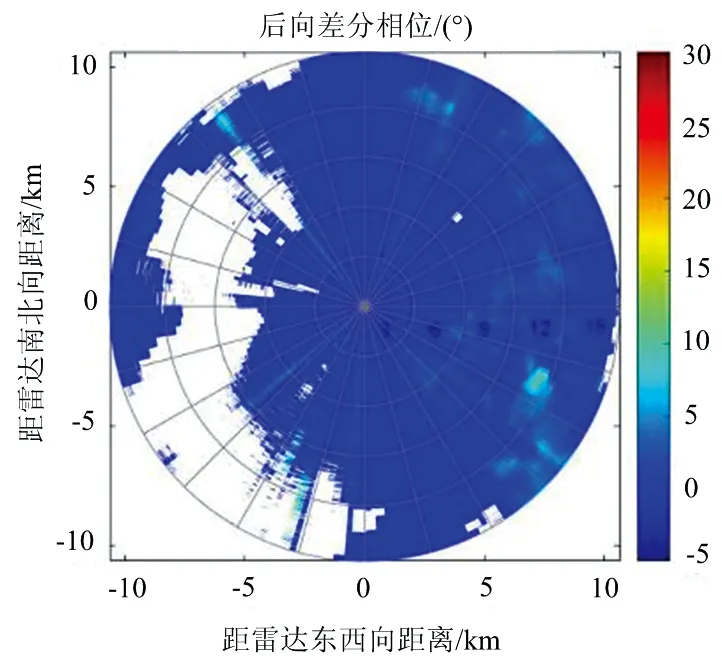
(b) 后向差分相位δdp

(c) 前向散射引起的差分相位Φdp圖5 差分相位分離所得參量PPI圖

對于上文提出的后向差分相位估計方法的準確性，可以通過觀察差分反射率因子Zdr，后向差分相位δdp顯示圖之間的匹配模式情況[15]。理論情況下，后向差分相位和差分反射率因子之間滿足式(6)。本文得到的后向差分相位是由實際測量得到的總差分相位減去重構得到的前向散射引起的差分相位。若得到的后向差分相位和差分反射率因子之間的散射關系基本滿足理論情況，則證明本文提出分離后向散射相位方法的可行性。

4 結束語

雷達實際測量得到的差分相位值可能會受到傳播路徑中其他單頻點電磁波或者非氣象雜波的影響，導致測量得到的后向差分相位的質量不高，利用雷達測量數據中同一徑向差分相位的變化特點以及相鄰徑向差分相位的特點，針對差分相位PPI圖中出現的無效數據點，突出雜點和條幅狀雜波進行處理。由于差分相移率在雷達數據處理中優越的性能，提出估計差分相移率和后向差分相位的方法。并可以將估計得到的后向差分相位和差分反射率之間的散射關系來驗證方法的準確性。

本文已經成功將上文提出的方法應用于代爾夫特理工大學X波段雙偏振雷達一組差分相位的估計。最終得到的差分相位符合理論上徑向變化的規律。