無線電能傳輸系統(tǒng)帶雙層有界磁屏蔽任意位置圓形線圈的耦合系數(shù)計算

李中啟 林志遠 楊 鵬 易吉良 黃守道

無線電能傳輸系統(tǒng)帶雙層有界磁屏蔽任意位置圓形線圈的耦合系數(shù)計算

李中啟1,2林志遠1楊 鵬1易吉良1黃守道2

（1. 湖南工業(yè)大學軌道交通學院 株洲 412007 2. 湖南大學電氣與信息工程學院 長沙 410082）

耦合系數(shù)是無線電能傳輸系統(tǒng)的關鍵參數(shù)之一，準確的耦合系數(shù)計算是優(yōu)化無線電能傳輸系統(tǒng)結構和提高傳輸效率的重要理論依據(jù)。目前還沒有帶雙層有界磁屏蔽任意位置圓形平面螺旋線圈之間的耦合系數(shù)計算方法。為此該文通過麥克斯韋方程組推導出雙層有界磁屏蔽條件下的矢量磁位表達式，利用邊界條件及空間幾何關系得到任意空間位置的耦合系數(shù)公式。與傳統(tǒng)的近似計算方法不同，該文所提出的耦合系數(shù)計算可以對圓形平面螺旋線圈間的耦合系數(shù)進行精確的數(shù)值求解。最后，以兩個圓形平面螺旋線圈間多種相對位置的變化情況為例，計算值、仿真值與實驗值吻合良好，驗證了所提計算方法的正確性。

無線電能傳輸 圓形線圈 磁屏蔽 耦合系數(shù)計算

0 引言

無線電能傳輸（Wireless Power Transfer, WPT）是一種在沒有任何物理連接的情況下電源和負載之間能量傳輸?shù)姆椒āＳ捎谄浞奖恪㈧`活、可靠和安全的優(yōu)勢，在電力電子領域引起了極大的關注，該技術有可能取代傳統(tǒng)的有線傳輸方法。目前正在研究將其納入工業(yè)設備[1]、軌道交通[2]、電動汽車[3-6]、消費電子[7-8]、生物醫(yī)學植入[9-10]和水下供電[11-12]中。然而，實際應用中常常會面臨初級線圈與初級線圈發(fā)生錯位偏移偏轉的情況，這會使WPT系統(tǒng)傳輸效率發(fā)生不同程度的變化。因此，研究初級線圈與次級線圈相對空間位置的變化對WPT耦合系數(shù)的影響具有重要意義。

隨著WPT應用范圍的擴大，其線圈結構也各式各樣，例如，矩形平面線圈、圓形平面線圈和六邊形幾何形狀等。為應對復雜的無線充電環(huán)境，加入了磁屏蔽材料來提升電磁屏蔽性能。在WPT中，耦合系數(shù)的大小與WPT效率緊密相關，而耦合系數(shù)和自感決定了互感。關于矩形平面線圈在WPT系統(tǒng)中的互感已有大量研究，分別通過Biot-Savart定律[13]、麥克斯韋方程[14]、傅里葉級數(shù)[15-16]、傅里葉-貝塞爾變換[17]和二階矢量位[18-19]對互感進行近似計算。但在對稱性上圓形線圈比矩形線圈更具優(yōu)勢，更加穩(wěn)定。

空氣介質圓形線圈間的互感計算方面，文獻[20-21]通過將圓形平面線圈劃分為等分的多邊形對圓形平面線圈在空氣中的互感進行精確計算，該方法的優(yōu)點是能夠預測邊形平面線圈的互感，但此方法當越大時計算量越大。文獻[22]通過矢量磁位來計算兩平面線圈在空氣中水平偏移的互感。文獻[23]利用已知的橢圓積分，推導出水平偏移圓柱薄壁線圈在空氣中和環(huán)之間的互感近似值表達式。文獻[24-25]提出了基于諾依曼公式的任意空間位置的線圈間互感的改進算法。文獻[26]基于Biot- Savart定律的分析模型，近似計算圓形和方形平面線圈在空氣中任意位置的互感。即使目前已有任意空間位置的互感計算方法的研究分析，但帶磁屏蔽材料的研究還很有限。

在磁屏蔽材料圓形線圈間互感計算方面，文獻[27]使用電流鏡像法計算單邊單層無限大尺寸磁屏蔽材料上圓形線圈間互感。文獻[28]通過應用貝塞爾-傅里葉變換和雙傅里葉變換推導了松耦合WPT系統(tǒng)中方形和圓形線圈互感計算的解析模型，并研究了自感、互感和耦合系數(shù)與基底的相對磁導率和線圈的線間距的關系。但該研究僅考慮了線圈橫向錯位帶雙邊單層無限大尺寸磁屏蔽材料的情況。文獻[29]提出一種基于電場強度和坐標變換法的互感計算新解析方法，可以快速計算雙層電磁屏蔽基板上任意相對位置圓形線圈之間的互感。但該文獻假設磁屏蔽材料是無窮大模型，而實際應用中磁屏蔽材料尺寸是有限的。綜上所述，目前帶多層有界磁屏蔽圓形線圈任意空間位置的耦合系數(shù)計算方法問題還沒有解決。

本文建立雙層有界磁屏蔽圓形平面螺旋線圈在任意位置變化情況的耦合系數(shù)計算模型。首先，通過麥克斯韋方程組推導出矢量磁位，再利用邊界條件獲得等量關系求解出相應系數(shù)；其次，通過空間幾何關系計算出旋轉參數(shù)；然后，通過諾依曼公式求解出互感與自感，從而計算出耦合系數(shù)；最后，通過仿真與實驗驗證了所提耦合系數(shù)計算方法的正確性。

1 耦合系數(shù)計算

本文耦合系數(shù)計算流程為：①系統(tǒng)模型具有磁屏蔽材料和空氣介質，因此可通過磁屏蔽材料和空氣介質的邊界將系統(tǒng)模型沿垂直方向劃分為六個區(qū)域；②通過麥克斯韋方程組推導出各個區(qū)域的矢量磁位；③利用相鄰區(qū)域的邊界條件建立等量關系，通過等量關系式求解出各個區(qū)域的未知系數(shù)；④通過諾依曼公式求解出互感表達式和自感表達式；⑤利用線圈間空間幾何關系求解出任意位置旋轉參數(shù)表達式；⑥將旋轉參數(shù)代入互感表達式得到任意位置互感表達式；⑦最后得到單邊雙層有界磁屏蔽圓形線圈間的耦合系數(shù)。

1.1 同軸線圈互感與自感計算

該模型使用兩個有限尺寸的磁屏蔽材料作為基底，建立雙層有界磁屏蔽圓形平面螺旋線圈的橫截面軸對稱如圖1所示。由于該模型為軸對稱模型，故建立柱坐標系（,,）。圖中，兩個磁屏蔽材料均為圓形基底。r1、1和r2、2分別為兩個磁屏蔽材料的磁導率和電導率。1、2分別為初級次級線圈半徑，p、s分別為初級、次級線圈距離磁屏蔽材料高度。為方便計算，將該模型由=p，=0，=1，=1+D和=2分為六個區(qū)域。初級線圈通入正弦電流ejt激勵，其中，為電流幅值，為角頻率，為時間變化量。

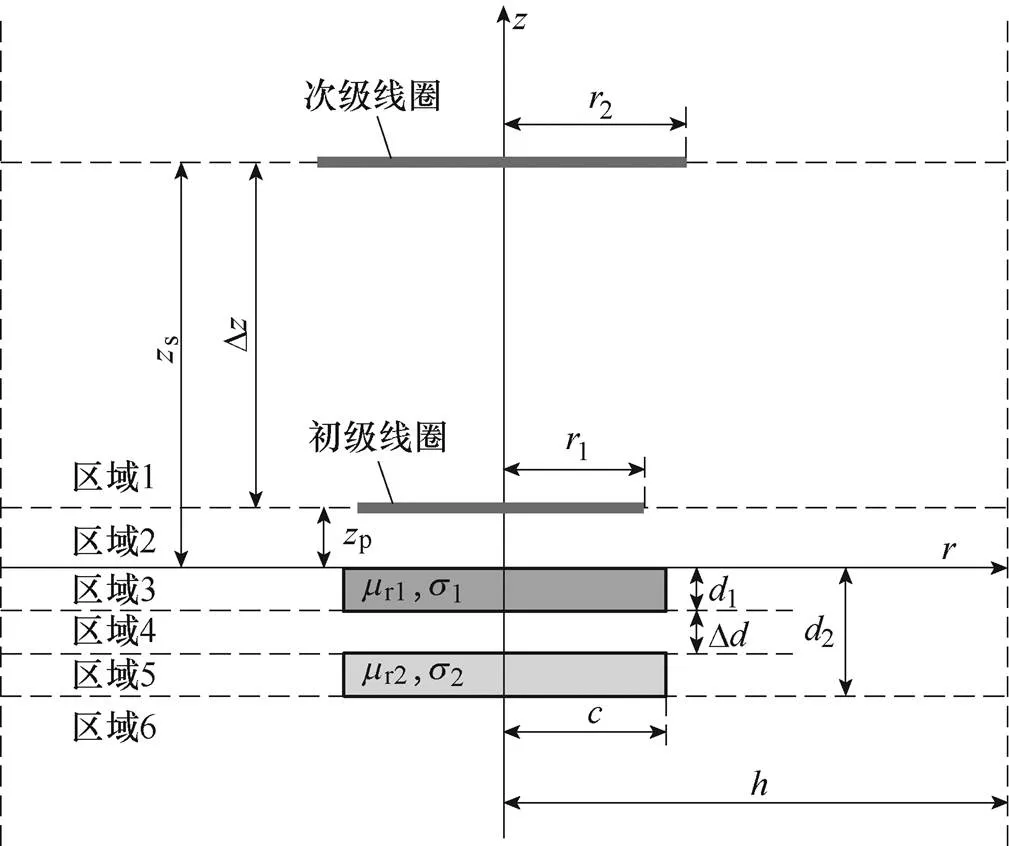
圖1 雙層有界磁屏蔽圓形平面螺旋線圈的橫截面軸對稱

根據(jù)圓形線圈產(chǎn)生的時變電磁場的特點，可得到矢量磁位。由于矢量磁位只有一個分量，并且沿方向呈均勻分布，則=。通過麥克斯韋方程組推導各區(qū)域矢量磁位（ =1, 2, 3, 4, 5, 6）滿足

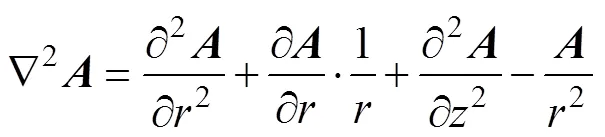
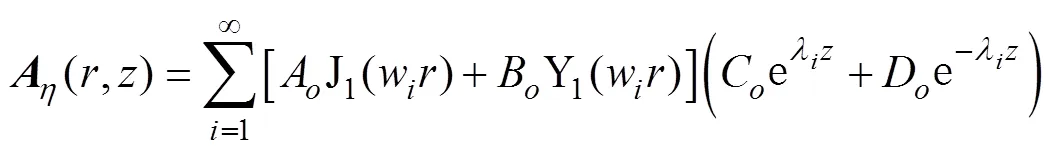
由于所求矢量磁位為有限值，當→0時，wr→0，Y1(wr)→∞，故B=0，則區(qū)域1, 2, 4, 6可推導為

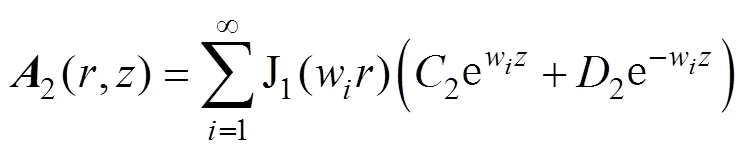
根據(jù)邊界條件，矢量磁位在某一截斷區(qū)域=時 (,)=0。式（4）～式（7）含指數(shù)函數(shù)部分不為0，故有J1(wh)=0，根據(jù)此條件可求解出特征值w。區(qū)域3、5含有磁屏蔽材料與空氣兩部分，此處以區(qū)域3為例，結合式（2）和式（3）可得

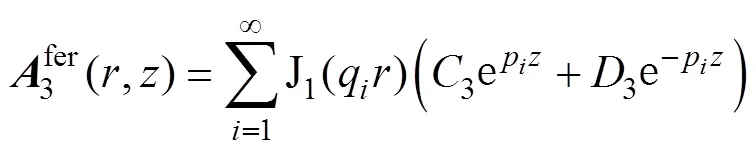
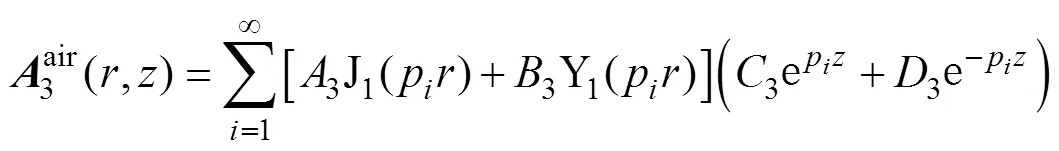
由于磁感應強度的法向分量和磁場強度的切向分量具有連續(xù)性，則當=時，其邊界條件滿足

聯(lián)立式（10）和式（11）得到系數(shù)3和3分別為

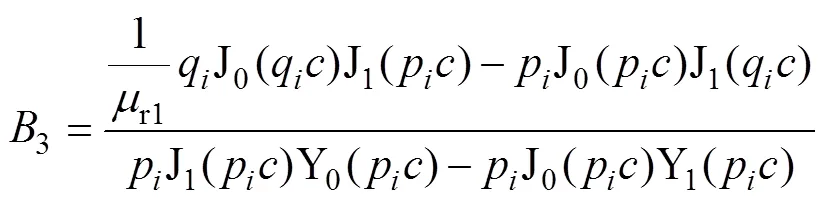
令1(pr)=AJ1(pr)+BY1(pr)，則式（9）可改寫為

式中，特征值q和p亦可通過1(ph)=0這一條件求解。同理可得區(qū)域5的關系式為

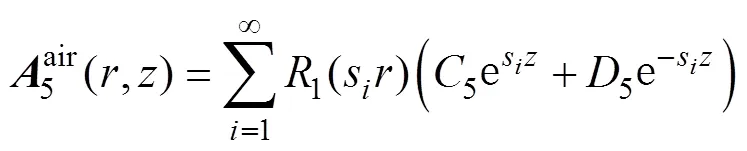
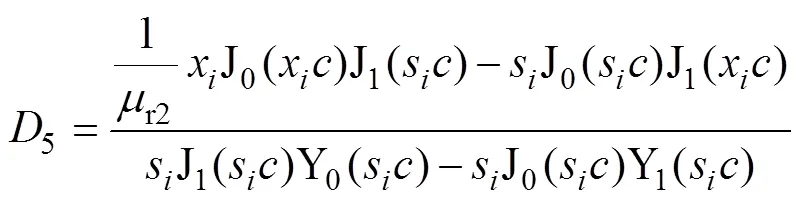
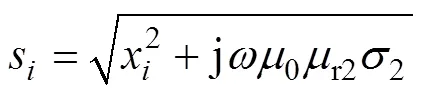
根據(jù)相鄰區(qū)域間的邊界條件的連續(xù)性，與磁感應強度的法向分量和磁場強度的切向分量的連續(xù)性可以得到

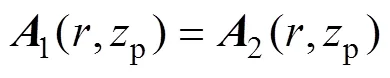
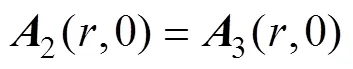
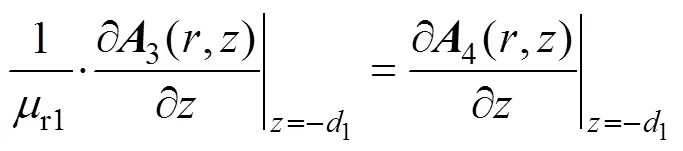
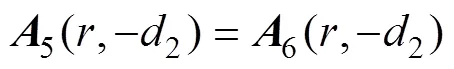
雖然所求解為無窮級數(shù)，但存在J1(wr)與Y1(wr)使得無窮級數(shù)快速收斂。為化簡推導，可以近似將解列寫為有限項求和解。以1(,)為例得

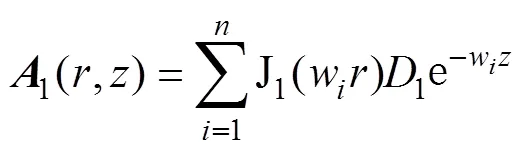
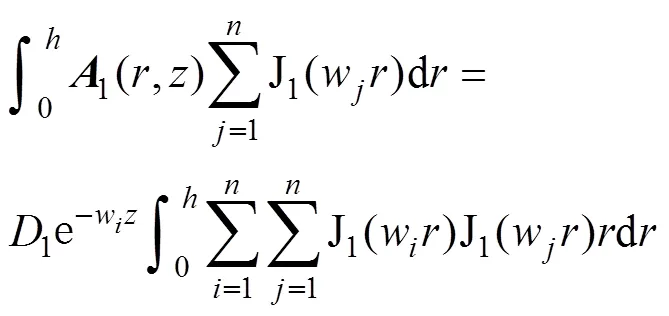
根據(jù)Bessel函數(shù)的正交性可進一步對式（30）化簡為

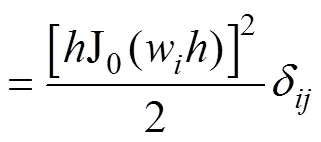
其中

將式（31）代入式（19）計算可得

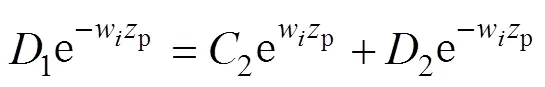
同理，式（20）～式（28）可以改寫為

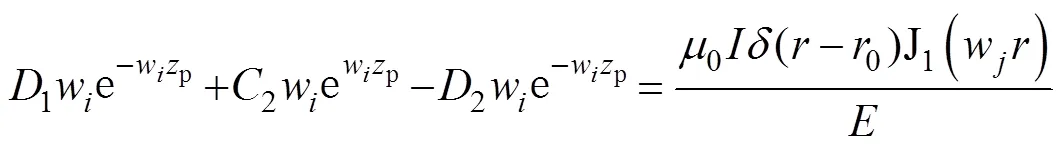
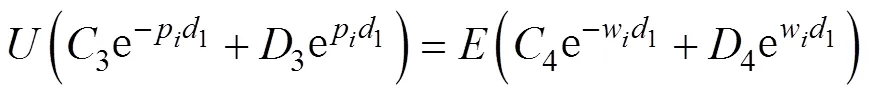
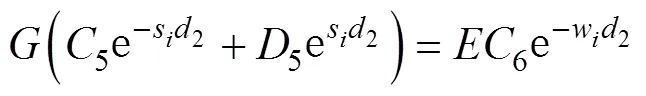
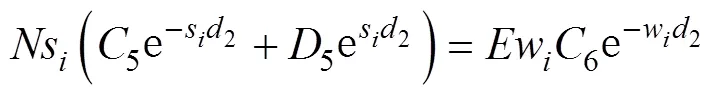
利用消元法或克萊姆法則或Matlab計算出2、3、4、5、6、1、2、3、4、5，其中、、、、為中間變量，即

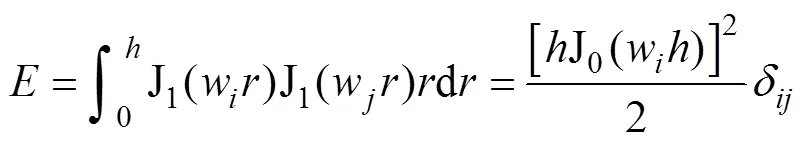
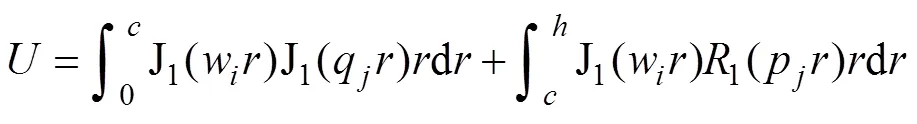
式（43）可根據(jù)Lommel積分公式進一步求解得

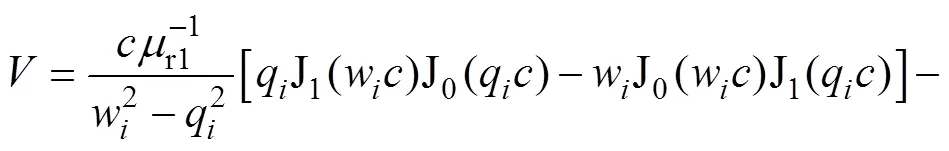
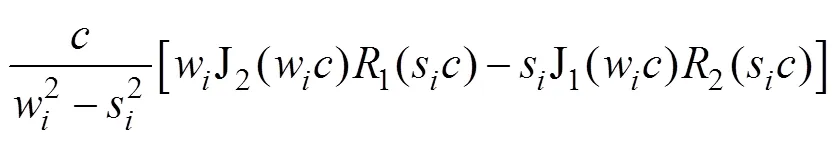
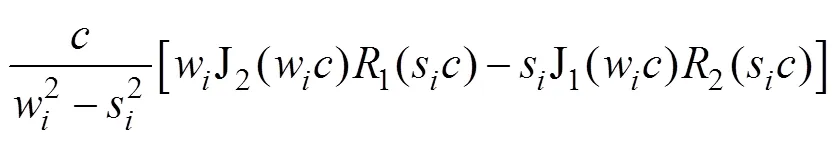
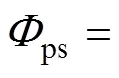
式中，2為沿次級線圈所在圓形的積分路徑。由于線圈為平面螺旋線圈，互感計算可近似為同心圓與同心圓間的互感，即

然而，實際線圈為多匝線圈，故總互感為

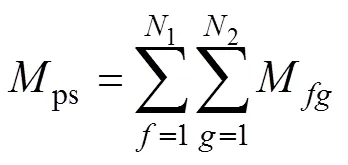
式中，1與2分別為初級線圈和次級線圈的匝數(shù)；、分別對應初級線圈和次級線圈處于第幾匝的線圈。

自感是由導體本身電流的變化而產(chǎn)生的電磁感應現(xiàn)象，在其計算方面，可以巧妙的將其理解為兩個規(guī)格一致的平面螺旋線圈距離無限接近時的互感，故依舊可以使用上述互感計算模型來計算自感。此處以初級線圈為例，由于兩平面螺旋線圈無限接近，計算時令s=p，代入式（49）計算得

即可得到單匝線圈的自感，再代入式（50）得到多匝線圈的自感為

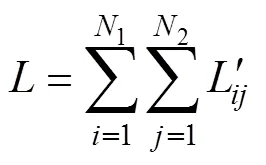
1.2 任意位置旋轉參數(shù)計算

為實現(xiàn)對平面螺旋線圈的任意位置的互感計算，需求出以1為圓心、以為半徑的圓Coil在點上的切線A與次級線圈在點上切線d間的夾角，即矢量磁位與線元d的夾角。任意相對位置雙層有界磁屏蔽圓形線圈互感計算系統(tǒng)框圖如圖2所示，為方便求解，構建以1為坐標原點的直角坐標系。次級線圈繞軸逆時針旋轉角度為（0°≤ ≤90°），沿軸平移距離，其余參數(shù)與第1.1節(jié)一致。

圖2 任意相對位置雙層有界磁屏蔽圓形線圈互感計算系統(tǒng)框圖

設次級線圈平面法向量為

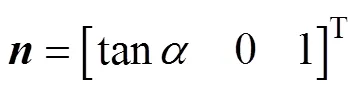
根據(jù)式（53）可以得到正交向量為

通過坐標運算求解出同時垂直于向量與向量的向量為

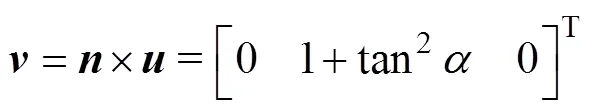
顯然，向量與向量均在次級線圈平面上，將向量、單位向量化為

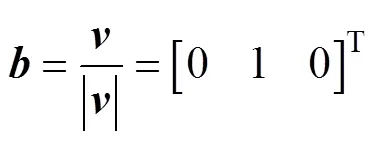
根據(jù)式（56）、式（57）及坐標2(, 0, 0)可得次級線圈的參數(shù)方程為

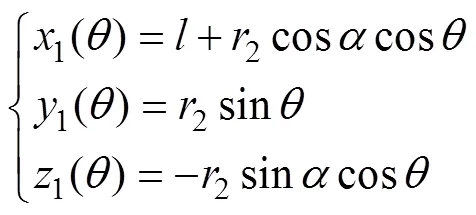
式（58）結合幾何關系可求出1長度為

分別對式（58）和式（60）中參數(shù)、求導得到圓Coil與次級線圈的任意點的切向量為

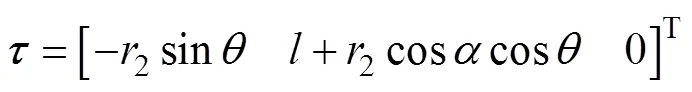
通過式（61）和式（62）可以求出任意空間的旋轉參數(shù)，即夾角的余弦為

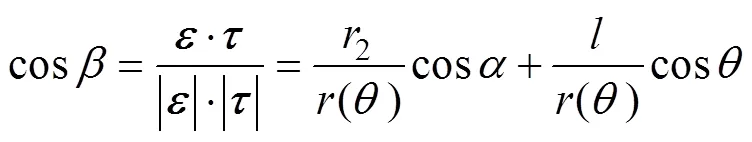
式中，0°≤ ≤90°，為擴大通式可求解的角度范圍，可通過圓形線圈的對稱性對式（63）改寫為

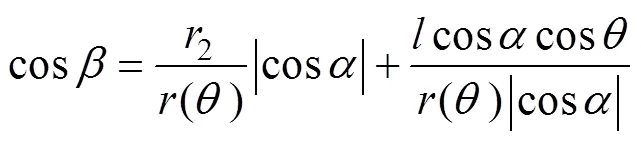
式中，0°≤ ≤180°。

1.3 耦合系數(shù)計算

結合1.2節(jié)任意位置旋轉參數(shù)cos與式（49），可推導出任意位置單匝線圈的互感公式為

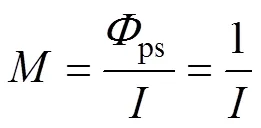
綜合所述，可以得到互感ps與初級線圈自感1、次級線圈自感2，則耦合系數(shù)為

2 仿真與實驗驗證

為驗證所提式（66）的有效性，通過有限元仿真軟件Ansys Maxwell搭建有限元仿真模型如圖3所示。由于本文討論無線電能傳輸系統(tǒng)在任意空間位置的耦合系數(shù)，故仿真與實驗驗證部分，將通過改變次級線圈的位置，測出其對應的互感與自感，分析耦合系數(shù)仿真值、實驗值與計算值之間的誤差。本節(jié)設置次級線圈垂直偏移、水平偏移、角度偏轉和水平偏移+角度偏轉四組數(shù)據(jù)進行驗證，其對應的線圈各狀態(tài)實驗模型如圖4所示。同時為測量實驗耦合系數(shù)中的互感值，研制了一套收發(fā)線圈裝置，實驗裝置如圖5所示，收發(fā)線圈與磁屏蔽材料的參數(shù)見表1。

圖3 有限元仿真模型

圖4 線圈各狀態(tài)實驗模型

圖5 實驗裝置

表1 線圈與磁屏蔽材料參數(shù)

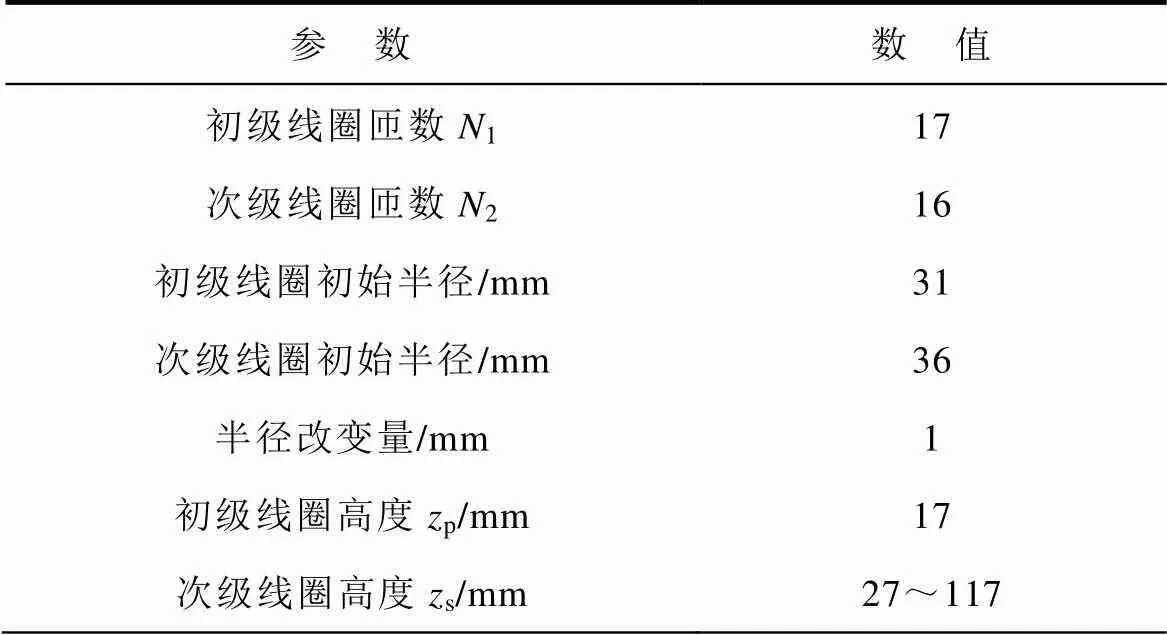
Tab.1 Coil and magnetic shielding material parameters

（續(xù)）

通過TH2829A阻抗分析儀進行電感測量，其電流頻率設為85kHz。實驗耦合系數(shù)中的互感測量方法：首先通過初級線圈與次級線圈同相連接，得到線圈兩端的電感為e1=1+2+2e；再將初級線圈與次級線圈反相連接，得到線圈兩端的電感為e2=1+2-2e。因此，初級線圈與次級線圈之間的互感=|e1-e2|/4。其中1為初級線圈自感，2為次級線圈自感。實驗互感測量原理如圖6所示。

圖6 實驗互感測量原理

2.1 垂直偏移

次級線圈沿軸正方向從s=27mm處以步長Ds=10mm依次進位至s=117mm，次級線圈垂直偏移示意圖如圖7所示。圖中，虛線為次級線圈上一時刻位置，實線為偏移后的相對位置。由于實際磁屏蔽材料間隙非常小，對耦合系數(shù)影響很小，故本文后續(xù)計算與仿真數(shù)據(jù)均以D=0進行計算。

圖7 次級線圈垂直偏移示意圖

測得垂直偏移時的耦合系數(shù)仿真值、計算值和實驗值及誤差見表2。表2中，D為次級線圈與初級線圈的距離，1、2和3分別為計算耦合系數(shù)、仿真耦合系數(shù)和實驗耦合系數(shù)。1為計算的耦合系數(shù)與仿真耦合系數(shù)之間的誤差，2為計算的耦合系數(shù)與實驗耦合系數(shù)之間的誤差。1和2表達式分別為

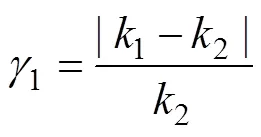
表2 垂直偏移時的耦合系數(shù)及誤差

Tab.2 Coupling coefficients and errors at vertical offsets

由于自感原則上不會變化，通過1.1節(jié)介紹的自感計算方法計算出初級線圈自感1=37.492mH，次級線圈自感2=36.877mH。

分析表2可得，次級線圈與初級線圈垂直距離為100mm時，計算的耦合系數(shù)與仿真耦合系數(shù)誤差1=3.71%外，計算的耦合系數(shù)與實驗耦合系數(shù)之間的誤差2=5.14%，其余誤差均不大于4.42%，體現(xiàn)出仿真、計算與實驗具有較好的一致性。在次級線圈垂直偏移的情況下，結合表2數(shù)據(jù)繪制出各項耦合系數(shù)隨垂直距離變化曲線如圖8所示。

分析圖8可知，次級線圈與初級線圈距離越近，耦合系數(shù)越高。隨著沿軸正方向距離的增大，磁通量減小，耦合系數(shù)逐漸減小，且隨著垂直距離的增大，耦合系數(shù)下降的趨勢也逐漸減小，這是由于在增加相同步長時，距離越遠，磁通量的改變越小。

圖8 耦合系數(shù)隨垂直距離變化曲線

2.2 水平偏移

次級線圈垂直距離s保持不變，此處設定s= 77mm，p=17mm。初級線圈與次級線圈之間垂直距離D=60mm。對次級線圈以步長為10mm沿軸正負方向水平偏移，范圍為-50～50mm，次級線圈水平偏移示意圖如圖9所示。

圖9 次級線圈水平偏移示意圖

測得耦合系數(shù)仿真值、計算值和實驗值及誤差分析見表3。表3中，為次級線圈垂直距離s=77mm時水平偏移量。

分析表3可知，計算的耦合系數(shù)與仿真耦合系數(shù)之間的誤差除次級線圈水平偏移至軸正半軸50mm處誤差1=2.09%外，其余誤差均不大于1.65%。計算耦合系數(shù)與實驗耦合系數(shù)之間誤差除次級線圈水平偏移至軸負半軸50mm處誤差2= 5.6%外，其余誤差均不大于2.65%。體現(xiàn)了仿真值、計算值與實驗值具有很好的一致性。在次級線圈水平偏移的情況下，結合表3數(shù)據(jù)繪制出各項耦合系數(shù)隨水平距離變化曲線如圖10所示。

表3 垂直距離s=77mm,p=17mm,D=60mm時水平偏移的耦合系數(shù)及誤差

圖10 耦合系數(shù)隨水平偏移距離變化曲線

分析圖10可知，耦合系數(shù)最高處次級線圈水平偏移距離為0mm，隨著次級線圈水平偏移距離的增加，磁通量減少，耦合系數(shù)逐漸降低。

2.3 角度偏轉

次級線圈與軸的距離s不變，此處設定s= 77mm。初級線圈與次級線圈圓心之間垂直距離D= 60mm，次級線圈繞軸逆時針旋轉角度為，步長為10°，次級線圈垂直偏轉示意圖如圖11所示。

實驗分析了范圍為0°～90°的耦合系數(shù)仿真值、計算值和實驗值見表4。為次級線圈垂直距離s=77mm時垂直偏轉量。

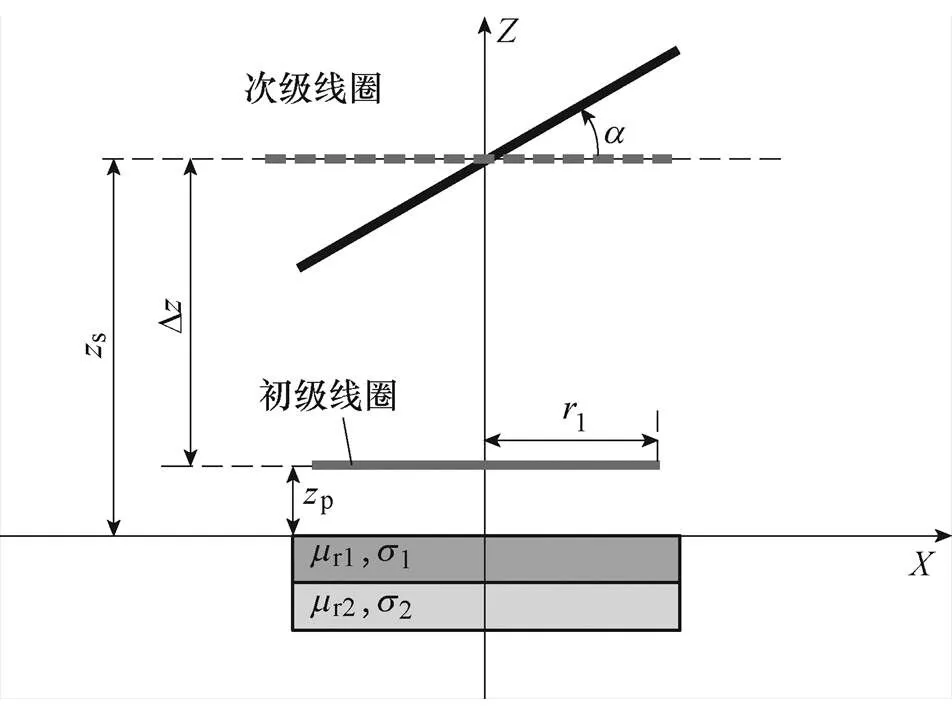
圖11 次級線圈垂直偏轉示意圖

表4 垂直距離s=77mm,D=60mm時垂直偏轉的耦合系數(shù)及誤差

Tab.4 Coupling coefficients and errors for vertical deflection at a vertical distance zs=77mm and Dz=60mm

分析表4可知，計算的耦合系數(shù)與仿真耦合系數(shù)之間的誤差1除旋轉角度為50°時誤差為4%外，其余誤差均不大于3.98%。計算耦合系數(shù)與實驗耦合系數(shù)之間的誤差2除旋轉角度為80°時誤差為5.29%外，其余誤差均不大于3.21%。由于旋轉角度為90°時，理論上將次級線圈視為垂直于初級線圈的細線，則磁通量應為零。但在仿真模型中，由于存在接口銜接部分的微小突起，故仿真時具有微小的磁通量。由于此處磁通量沒有實際意義，故未作實驗對照組以及誤差分析，仿真值、計算值與實驗值具有良好的一致性。在次級線圈垂直偏轉的情況下，結合表4數(shù)據(jù)繪制出各項耦合系數(shù)隨垂直偏轉角度變化曲線如圖12所示。

圖12 耦合系數(shù)隨垂直偏轉角度變化曲線

分析圖12可知，次級線圈垂直偏轉角度為0°～50°時，耦合系數(shù)無明顯下降，且在次級線圈垂直偏轉角度為10°～40°時，耦合系數(shù)有微小提升，這是由于次級線圈比初級線圈大。在垂直偏轉10°～40°時，次級線圈向面的投影面積基本在初級線圈內(nèi)，且在偏轉過程中內(nèi)徑逐漸減小，與初級線圈逐漸對齊，磁通量有微小的提升，故有此現(xiàn)象。次級線圈垂直偏轉角度為50°～90°與初級線圈對齊面積減小，故耦合系數(shù)逐漸下降。

2.4 水平偏移加角度偏轉

次級線圈與軸的距離s不變，此處設定s= 77mm。初級線圈與次級線圈圓心之間垂直距離D= 60mm，次級線圈繞軸順時針旋轉角度為，此處設定 =-20°，對次級線圈以步長為10mm沿軸正負方向水平偏移，范圍為-50～50mm，次級線圈水平偏移加角度偏轉示意圖如圖13所示。

圖13 次級線圈水平偏移加角度偏轉示意圖

測得s=77mm， =-20°時耦合系數(shù)仿真值、計算值和實驗值及誤差分析見表5。表中，為次級線圈垂直距離s=77mm，垂直偏轉 =-20°時水平偏移量。

表5s=77mm,D=60mm, =-20°時耦合系數(shù)計算值、仿真值和實驗值及誤差

Tab.5 Calculated, simulated and experimental values of coupling coefficients and errors for zs=77mm, Dz=60mm and a =-20°

分析表5可知，除計算的耦合系數(shù)與仿真耦合系數(shù)誤差1在沿軸負方向40mm時為5.15%外，其余計算的耦合系數(shù)與仿真耦合系數(shù)間誤差1≤4.99%。計算耦合系數(shù)與實驗耦合系數(shù)間誤差2≤4.71%。仿真值、計算值與實驗值具有較好的一致性。在沿軸負方向水平偏移時，計算的耦合系數(shù)與仿真耦合系數(shù)間誤差1比沿軸正方向水平偏移時計算的耦合系數(shù)與仿真耦合系數(shù)間誤差1大，這是由于仿真模型閉合線圈的銜接處的導線在旋轉后偏下，仿真值偏大，因此誤差相對較大。在次級線圈水平偏移加角度偏轉的情況下，結合表5數(shù)據(jù)繪制出各項耦合系數(shù)隨水平偏移距離變化曲線如圖14所示。

分析圖14可知，耦合系數(shù)最高處次級線圈水平偏移距離為0mm，隨著次級線圈水平偏移距離的增加，磁通量減少，耦合系數(shù)逐漸降低，且次級線圈沿軸正半軸水平偏移時耦合系數(shù)比次級線圈沿軸負半軸水平偏移時耦合系數(shù)下降的趨勢小，這是由于次級線圈繞軸順時針旋轉20°，沿軸正半軸水平偏移時所接收到的磁通量大于次級線圈沿軸負半軸水平偏移時所接收到的磁通量，故有此 現(xiàn)象。

圖14 耦合系數(shù)隨水平偏移距離變化曲線

3 結論

本文提出了一種無線電能傳輸系統(tǒng)帶雙層有界磁屏蔽圓形平面螺旋線圈任意空間位置的耦合系數(shù)計算方法。通過麥克斯韋方程組推導出矢量磁位公式，利用各區(qū)域的邊界條件得到各區(qū)域的矢量磁位的對應關系式，最后推導出耦合系數(shù)計算公式，并通過仿真與實驗對計算結果進行驗證。本文提出的耦合系數(shù)計算模型可以實現(xiàn)線圈間任意空間位置，且?guī)щp層有界不同材質磁屏蔽材料的計算，比現(xiàn)有圓形平面螺旋線圈的耦合系數(shù)計算模型更具一般性。研究結果為線圈設計和參數(shù)優(yōu)化提供了理論依據(jù)，對下一步雙邊雙層有界磁屏蔽耦合系數(shù)的研究也具有一定借鑒意義。

[1] 蘇玉剛, 劉家鳴, 王智慧, 等. 磁耦合機構拾取線圈平面金屬的影響及其抑制方法[J]. 電工技術學報, 2022, 37(3): 578-588.

Su Yugang, Liu Jiaming, Wang Zhihui, et al. Influence analysis of metal in the same plane with pickup coil on magnetic coupler and suppression method[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 578-588.

[2] 陳凱楠, 蔣燁, 檀添, 等. 軌道交通350kW大功率無線電能傳輸系統(tǒng)研究[J]. 電工技術學報, 2022, 37(10): 2411-2421, 2445.

Chen Kainan, Jiang Ye, Tan Tian, et al. Research on 350kW high power wireless power transfer system for rail transit[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2411-2421, 2445.

[3] 趙靖英, 張振遠, 張珂. 基于∞非線性控制器的電動汽車無線充電系統(tǒng)的副邊控制設計與參數(shù)優(yōu)化[J]. 電工技術學報, 2022, 37(3): 566-577.

Zhao Jingying, Zhang Zhenyuan, Zhang Ke. Control design and parameter optimization on secondary side of electric vehicle wireless charging system based on∞nonlinear controller[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 566-577.

[4] 周瑋, 藍嘉豪, 麥瑞坤, 等. 無線充電電動汽車V2G模式下光儲直流微電網(wǎng)能量管理策略[J]. 電工技術學報, 2022, 37(1): 82-91.

Zhou Wei, Lan Jiahao, Mai Ruikun, et al. Research on power management strategy of DC microgrid with photovoltaic, energy storage and EV-wireless power transfer in V2G mode[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 82-91.

[5] 劉闖, 郭贏, 葛樹坤, 等. 基于雙LCL諧振補償?shù)碾妱悠嚐o線充電系統(tǒng)特性分析與實驗驗證[J]. 電工技術學報, 2015, 30(15): 127-135.

Liu Chuang, Guo Ying, Ge Shukun, et al. Characteri- stics analysis and experimental verification of the double LCL resonant compensation network for elec- trical vehicles wireless power transfer[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(15): 127-135.

[6] 陳琛, 黃學良, 譚林林, 等. 電動汽車無線充電時的電磁環(huán)境及安全評估[J]. 電工技術學報, 2015, 30(19): 61-67.

Chen Chen, Huang Xueliang, Tan Linlin, et al. Elec- tromagnetic environment and security evaluation for wireless charging of electric vehicles[J]. Transactions of China Electrotechnical Society, 2015, 30(19): 61-67.

[7] Zhu Jiaqi, Ban Yongling, Xu Ruimin, et al. An NFC- CPT-combined coupler with series-none compensation for metal-cover smartphone applications[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(3): 3758-3769.

[8] 姚若玉, 曲小慧, 郁繼棟, 等. 自適應電池充電曲線的三線圈電池無線充電器[J]. 電力系統(tǒng)自動化, 2022, 46(7): 170-177.

Yao Ruoyu, Qu Xiaohui, Yu Jidong, et al. Three-coil wireless battery charger with self-adaptation to battery charging curve[J]. Automation of Electric Power Systems, 2022, 46(7): 170-177.

[9] Sedehi R, Budgett D, Jiang Jincheng, et al. A wireless power method for deeply implanted biomedical devices via capacitively-coupled conductive power transfer[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 1870-1882.

[10] Narayanamoorthi R. Modeling of capacitive resonant wireless power and data transfer to deep biomedical implants[J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2019, 9(7): 1253-1263.

[11] Yang Lei, Zhang Yuanqi, Li Xiaojie, et al. Analysis and design of four-plate capacitive wireless power transfer system for undersea applications[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(3): 202-211.

[12] 蘇玉剛, 錢林俊, 劉哲, 等. 水下具有旋轉耦合機構的電場耦合無線電能傳輸系統(tǒng)及參數(shù)優(yōu)化方法[J]. 電工技術學報, 2022, 37(10): 2399-2410.

Su Yugang, Qian Linjun, Liu Zhe, et al. Underwater electric-filed coupled wireless power transfer system with rotary coupler and parameter optimization method[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2399-2410.

[13] Kim J, Son H C, Kim D H, et al. Efficiency of magnetic resonance WPT with two off-axis self-resonators[C]// 2011 IEEE MTT-S International Microwave Work- shop Series on Innovative Wireless Power Trans- mission: Technologies, Systems, and Applications, Kyoto, Japan, 2011: 127-130.

[14] Itaya T, Miki K, Takehira N, et al. Eddy current distribution for a rectangular coil arranged parallel to a moving conductor slab[J]. IET Science, Measure- ment & Technology, 2012, 6(2): 43-51.

[15] Kushwaha B K, Rituraj G, Kumar P. 3-D analytical model for computation of mutual inductance for different misalignments with shielding in wireless power transfer system[J]. IEEE Transactions on Transportation Electrification, 2017, 3(2): 332-342.

[16] 李中啟, 李晶, 全倡輝, 等. 無線電能傳輸系統(tǒng)帶磁屏蔽任意位置矩形線圈的互感計算[J]. 電工技術學報, 2022, 37(17): 4294-4305.

Li Zhongqi, Li Jing, Quan Changhui, et al. Mutual inductance calculation of arbitrarily positioned rectangular coils with magnetic shielding in wireless power transfer systems[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4294-4305.

[17] Luo Zhichao, Wei Xuezhe. Theoretical analysis of planar spiral coils between two multilayer media for electric vehicle wireless charging[J]. Energies, 2018, 11(4): 693.

[18] 郝寬勝, 黃松嶺, 趙偉, 等. 基于二階矢量位的矩形截面回折線圈阻抗和脈沖磁場的解析建模與計算[J]. 物理學報, 2011, 60(7): 784-793.

Hao Kuansheng, Huang Songling, Zhao Wei, et al. Analytical modelling and calculation of impedance and pulsed magnetic field for rectangular meander coil based on second order potential[J]. Acta Physica Sinica, 2011, 60(7): 784-793.

[19] 吳德會, 何天府, 王曉紅, 等. 感應電能傳輸中矩形螺線線圈互感耦合的解析建模與分析[J]. 電工技術學報, 2018, 33(3): 680-688.

Wu Dehui, He Tianfu, Wang Xiaohong, et al. Analytical modeling and analysis of mutual indu- ctance coupling of rectangular spiral coils in inductive power transfer[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 680-688.

[20] Tavakkoli H, Abbaspour-Sani E, Khalilzadegan A, et al. Mutual inductance calculation between two coaxial planar spiral coils with an arbitrary number of sides[J]. Microelectronics Journal, 2019, 85: 98-108.

[21] Y?ld?r?z E, Kemer S B. Novel semi-analytical method for mutual inductance calculation of the thin spiral disk coils[J]. IET Electric Power Applications, 2019, 13(10): 1607-1612.

[22] Song Kaihong, Feng Jian, Zhao Ran, et al. A general mutual inductance formula for parallel non-coaxial circular coils[J]. Applied Computational Electro- magnetics Society Journal, 2019, 34(9): 1385-1390.

[23] Compter J. Mutual inductance and forces between two non-coaxial co-planar circular thin-wall air coils[J]. Compel, 2019, 38(1): 216-231.

[24] Wang Yiming, Xie Xu, Zhou Yan, et al. Calculation and modeling analysis of mutual inductance between coreless circular coils with rectangular cross section in arbitrary spatial position[C]//2020 IEEE 5th Infor- mation Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 2020: 1258- 1267.

[25] Qian Libo, Chen Mengfei, Cui Kexue, et al. Modeling of mutual inductance between two misalignment planar coils in wireless power transfer[J]. IEEE Microwave and Wireless Components Letters, 2020, 30(8): 814-817.

[26] Luo Zhichao, Wei Xuezhe. Mutual inductance analysis of planar coils with misalignment for wireless power transfer systems in electric vehicle[C]//2016 IEEE Vehicle Power and Propulsion Conference (VPPC), Hangzhou, China, 2016: 1-6.

[27] Roshen W A. Effect of finite thickness of magnetic substrate on planar inductors[J]. IEEE Transactions on Magnetics, 1990, 26(1): 270-275.

[28] Luo Zhichao, Wei Xuezhe. Analysis of square and circular planar spiral coils in wireless power transfer system for electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 331-341.

[29] Zhang Xueyi, Quan Changhui, Li Zhongqi. Mutual inductance calculation of circular coils for an arbitrary position with electromagnetic shielding in wireless power transfer systems[J]. IEEE Transa- ctions on Transportation Electrification, 2021, 7(3): 1196-1204.

Calculation of The Coupling Coefficient of an Arbitrarily Positioned Circular Coil for Wireless Power Transfer System with a Double-Layered Finite Magnetic Shield

1,21112

（1. College of Railway Transportation Hunan University of Technology Zhuzhou 412007 China 2. College of Electrical and Information Engineering Hunan University Changsha 410082 China）

The coupling coefficient is one of the critical parameters in the wireless power transfer system. Its accurate calculation is vital for optimizing the structure of the wireless power transfer system and enhancing the transfer efficiency. However, there is no method for calculating the coupling coefficient between circular planar spiral coils with double-layered finite magnetic shields at an arbitrary position. In this paper, the expression of vector magnetic potential under the condition of a double-layer finite magnetic shield is derived from Maxwell's equations. Moreover, the equation of the coupling coefficient for an arbitrary position is obtained using the boundary conditions and geometric spatial relations. Different from the traditional approximate calculation method, the proposed coupling coefficient calculation can solve the exact coupling coefficient between circular planar spiral coils. Finally, taking various relative positions between two circular planar spiral coils as an example, the calculation, simulation, and experimental results are in good agreement, which verifies the correctness of the proposed calculation method.

Wireless power transfer, circular coils, magnetic shield, calculation of coupling coefficients

10.19595/j.cnki.1000-6753.tces.220478

TM724

國家自然科學基金項目（11901188）、湖南省教育廳項目（20B186, 18A272）和湖南省自然科學基金項目（2019JJ60055）資助。

2022-04-01

2022-06-08

李中啟 男，1985年生，博士，研究生導師，研究方向為無線電能傳輸技術。E-mail: lizhongqi@hnu.edu.cn

黃守道 男，1962年生，教授，博士，博士生導師，研究方向為特種電機本體及控制、無線電能傳輸技術。E-mail: hsd1962@hnu.edu.cn（通信作者）

（編輯 陳 誠）