帶內全雙工水聲通信空間域自干擾抵消方法

陸胤亨，趙云江，青 昕，*，楊晨璐，吳頌文

（1.哈爾濱工程大學 水聲技術重點實驗室，黑龍江 哈爾濱 150001；2.海洋信息獲取與安全工信部重點實驗室（哈爾濱工程大學）工業和信息化部，黑龍江 哈爾濱 150001；3.哈爾濱工程大學 水聲工程學院，黑龍江 哈爾濱 150001；4.中國船舶集團有限公司第七一〇研究所，湖北 宜昌 443003；5.清江創新中心，湖北 武漢 430076）

0 引言

如何在水聲通信帶寬嚴重受限的情況下提高水聲通信網絡的頻譜效率及系統信息吞吐量，是未來水聲通信網絡技術急需解決的問題。帶內全雙工水聲通信（In-Band Full Duplex Underwater Acoustic Communication，IBFD-UWAC）技術目的在于實現通信雙方同時發送、接收相同頻段信號，相比于傳統半雙工模式，頻率效率提升了1倍，且一定程度上加大了通信系統的安全性。對于帶內全雙工水聲通信系統而言，其關鍵問題在于如何實現自干擾抵消（SIC），對于模擬域及數字域自干擾抵消，目前由于硬件設備限制，自干擾抵消性能存在上限[1-5]。

針對空間域自干擾抵消（Spatial Self Interference Cancellation，SSIC）學者們提出了帶內全雙工水聲通信系統的空間域自干擾抵消方法，文獻[6]所述的全雙工水聲通信機利用矢量水聽器零點抵消特性降低了接收到的自干擾信號強度。文獻[7]所述的全雙工水聲通信系統采用帶指向性發射換能器，獲得了約25 dB的干擾抵消效果。而聲障板由于重量、體積等因素，在工程應用起來較為復雜，指向性換能器具有硬件依賴性，且抑制能力有限，靈活度較差，空間域自干擾抑制目的不是完美的抵消自干擾信號，而是避免期望信號埋沒在量化噪聲中。文獻[8]提到了一種數字–空間域聯合自干擾抵消方法。與大多數依靠模擬自干擾抵消的方法不同，該方法依靠數字發射波束成形來降低自干擾。該方法目的不在于完全消除自干擾，而是試圖充分降低自干擾，以防止淹沒接收機的動態范圍。空間域抵消后，殘余的自干擾隨后被接收器在數字域中消除。文獻[9]中提到了空間–數字域聯合自干擾抵消方法，該方法采用凸優化理論完成了針對帶內全雙工水聲通信系統的波束形成器的設計，并與數字域聯合完成了多域聯合抵消，與傳統方法相比抵消效果具有很大提升。

針對各頻率分量響應不一致的問題，早期方法是通過不同尺寸的子陣接收信號各頻率數據[10]，但此方法硬件結構復雜且無法做到全頻帶恒定束寬。后來研究者們對不同子帶頻點設計不同加權矢量實現這些中心頻點的波束寬度恒定。主要有空間重采樣法[11-12]、基于傅里葉變換的擬合方法[13-15]、Bessel 函數算法[16]等。而在 IBFD-UWAC系統實際應用中，往往需要根據陣列形狀設計具有特殊響應的波束形成器[17-18]，此過程主要考慮保持主瓣恒定波束響應一致且抑制具有陣列依賴性的干擾源，且干擾源來自近場，需要進行近場效應補償。

通過上述分析得知，IBFD-UWAC系統中以往少有研究利用陣列信號處理完成自干擾抵消，且在波束形成器設計過程中，忽略了近場效應問題，即：帶內全雙工水聲通信系統中自干擾信號通常來自于近場，若不進行近場補償，則空域濾波達不到預期抵消效果。為進一步增加空間域自干擾抵消效果，提高SIC上限，本文對IBFD-UWAC系統的近場效應進行了補償，并根據當前應用場景下自干擾源的位置信息，設計凸優化問題，從而得到陣列的最優權值，完成空間域自干擾抵消，并將所提出的方法在水池環境中做了實驗驗證。

1 基本原理

本文所述的帶內全雙工水聲通信節點通信模型如圖1所示。

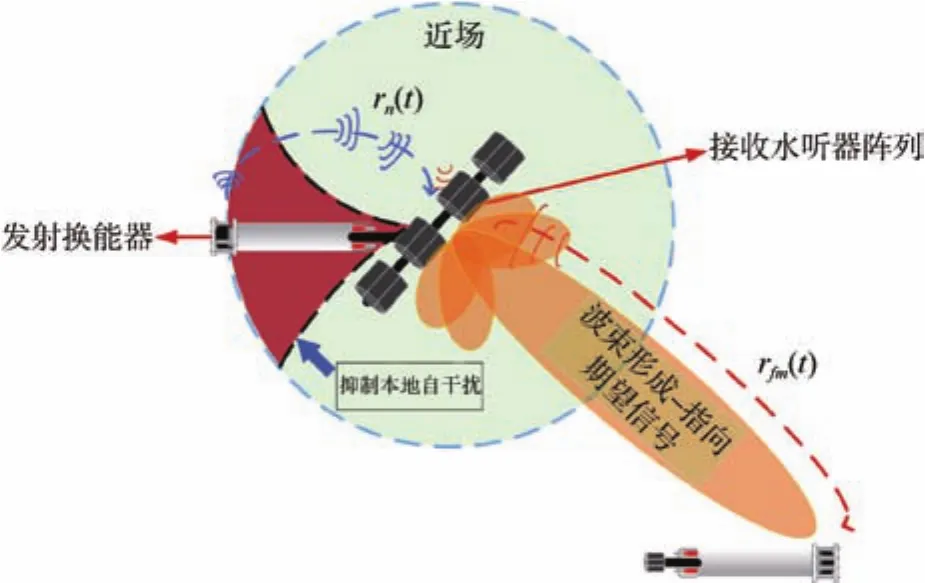
圖1 帶內全雙工水聲通信節點通信模型Fig.1 Communication model of in-band full-duplex underwater acoustic communication node

波束形成技術是一種常用的干擾抵消技術，其不僅被廣泛應用于無線電研究領域中，也被應用在了水聲領域。本文將其應用于 IBFD-UWAC系統中，陣列接收信號后，在空間域進行波束形成，完成空間域自干擾抵消，降低接收信號的信干比（Signal Interference Ratio，SIR），圖2展示當陣元數為4時，陣列全雙工水聲通信機的應用場景。

圖2 水下通信領域陣列信號處理應用場景Fig.2 Application scenario of array signal processing in underwater communication field

對于水聲通信系統來說，M個陣元對聲波進行空間采樣，在t時刻系統輸出的信號y(t)為空間樣本xm(t)的線性組合，即

式中：wm表示第m個陣元的權值系數；*表示復共軛。

假設輸入信號是沖激復平面波ejwt，其角頻率為w，到達角為θ（θ?[-π/2,π/2]），如圖3所示。假設第一個陣元接收信號相位為0，則第一個陣元接收信號為x0(t)=ejwts；第m個陣元接收信號xm-1（t）=ejw（t-τm），其中τm為波從第一個水聽器到第m個水聽器的傳播時延，是一個關于到達角θ的函數。此時波束形成器輸出為

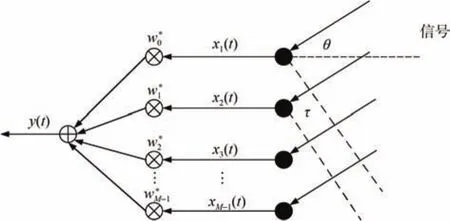
圖3 遠場條件下陣元接收示意圖Fig.3 Schematic diagram of array element receiving under far-field condition

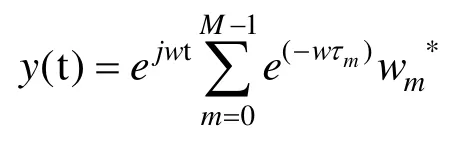
式中，τ0=0。

波束形成器的響應為

式中：向量w包含M個傳感器的復共軛系數；H表示共軛轉置，即

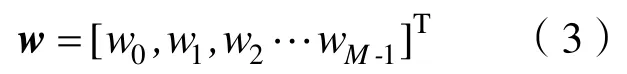
式中：T表示轉置；向量a(w,)θ為陣列響應向量，也稱為導向矢量，即

假設陣元間距d=λ/2，其中λ為波長，那么

則窄帶波束形成器響應寫為

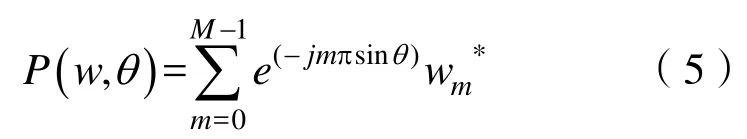
值得說明的是：本文提出的SSIC方法采用頻域寬帶波束形成器，核心是通過傅里葉變換將數據從時域轉換到頻域的多個子帶，每個子帶滿足窄帶條件，上述窄帶波束設計方法可以直接使用。具體使用步驟如下：首先將信號通過DFT（離散傅里葉變換），將信號轉換至頻域，在頻域內，劃分出不同頻點，在每個子頻帶內運用窄帶波束形成方法，最后將波束形成器的輸出利用 IDFT（離散傅里葉變換的逆變換）至時域，圖4為頻域寬帶波束形成的流程框圖。

圖 4 頻域寬帶波束形成流程Fig.4 Frequency domain broadband beamforming process

近場信號的波為球面波，接收信號間的幅度差別較大，這增加了信號處理的難度。近場在r＜ 2L2/λ的范圍內生效，r為聲源到參考陣元的距離，L為最大陣列孔徑，λ為工作波長。近場中可以分為窄帶和寬帶2種模型討論。而在帶內全雙工水下通信系統中，通常采用寬帶信號通信。故本文中的近場信號為寬帶信號。

圖 5 近場條件下陣元接收示意圖Fig.5 Schematic diagram of array element receiving under near-field condition

本文在文獻[9]基礎之上設計了一個近場條件下的恒定束寬波束形成器，該波束形成器可以針對具有方向與陣型依賴的干擾來源方向形成“零陷”，同時保持主瓣的波束響應頻率不變性，并通過凸優化方程補償近場效應。本文設計的空間域自干擾抵消方法針對 IBFD-UWAC中陣列依賴的本地干擾源，利用凸優化方法抵消陣列依賴的近場干擾方位的SI信號。

本文基于文獻[9]，具體凸優化過程設計如下：

2）將上述設計的波束形成器中心頻率處的主瓣響應作為凸優化過程的期望響應pdesired（θ），并使優化后的波束形成器響應pMF（θ）在帶有pdesired（θ）的主瓣角度區間θMF（θ）中的雙參數響應最小。

3）利用凸優化理論，將側擺角區間θSF內的波束響應pSF（θ）約束在設定值ξSF以下，將零陷區間θZF內的波束響應pZF（θ）約束在設定值ξZF以下。為獲得更好的自干擾抵消效果，修改了凸優化方程，即在保證主瓣設計波束與期望波束加權誤差小于某期望值的條件下，使得零陷角度波束響應最低。

4）使用IFFT還原信號，得到SSIC后的信號。

綜合上述步驟，本文構造了凸優化方程：

為便于利用 SeDuMi計算，本文將式（7）變換為：

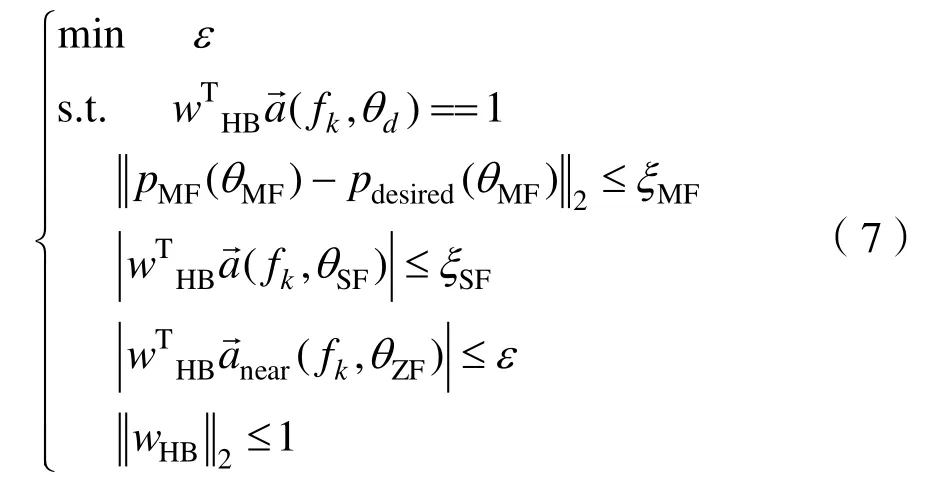
其中引入一組新的非負變量，εm，m=1,2,…,M，

令

求解在每個頻點下地最優權值向量，即每個陣元的加權系數。

由于在SeDuMi中，標準的凸錐問題形式定義為

式中：y中含有期望權值；A是任意系數矩陣；b和c是任意向量；K是一個對稱錐集合；其中A，b，c的維數是匹配的；q維二階錐定義為

等式約束可以表示為

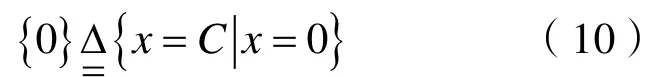
最后問題轉換成：

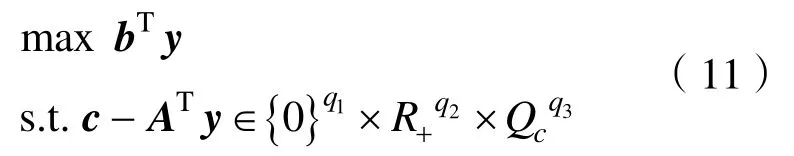
式（12）可以利用SeDuMi工具箱進行分段求解，因此本文將式（8）轉換為q1個等式約束，q2個線性約束和q3個二階錐。

式（8）中的第一項等式

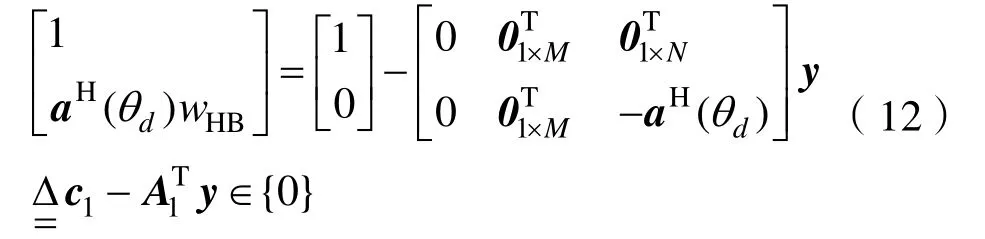
式（8）中的不等式可用二階錐表示為

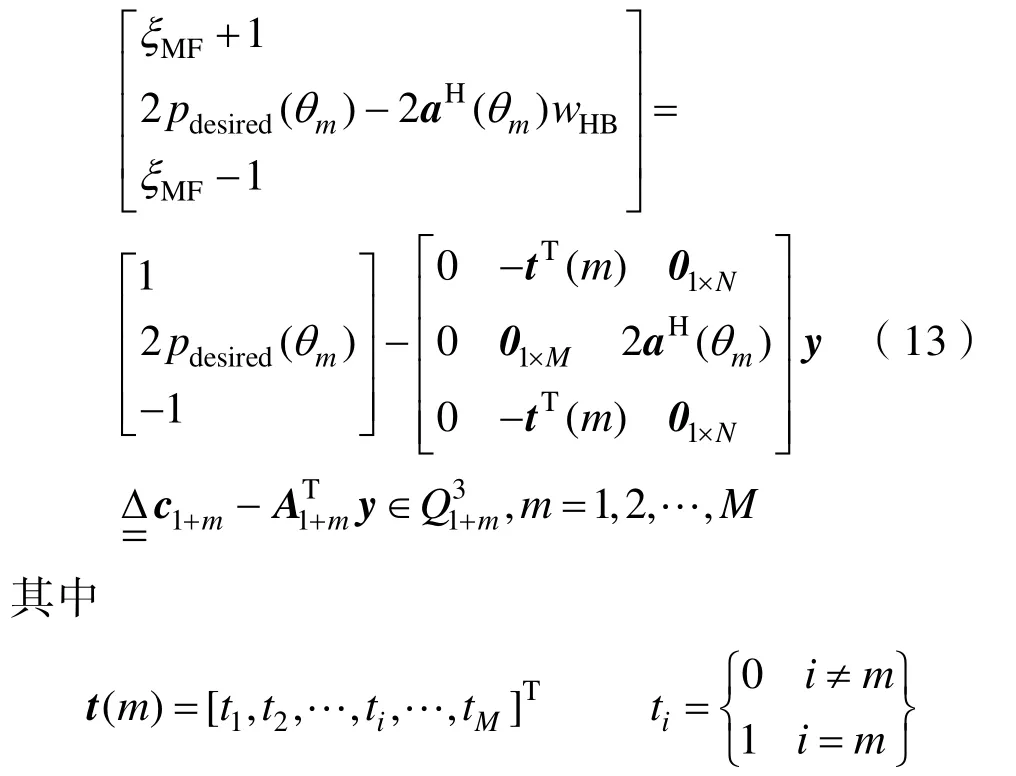
為方便計算，式（8）中最后3個不等式轉換為式（15）–（17）。

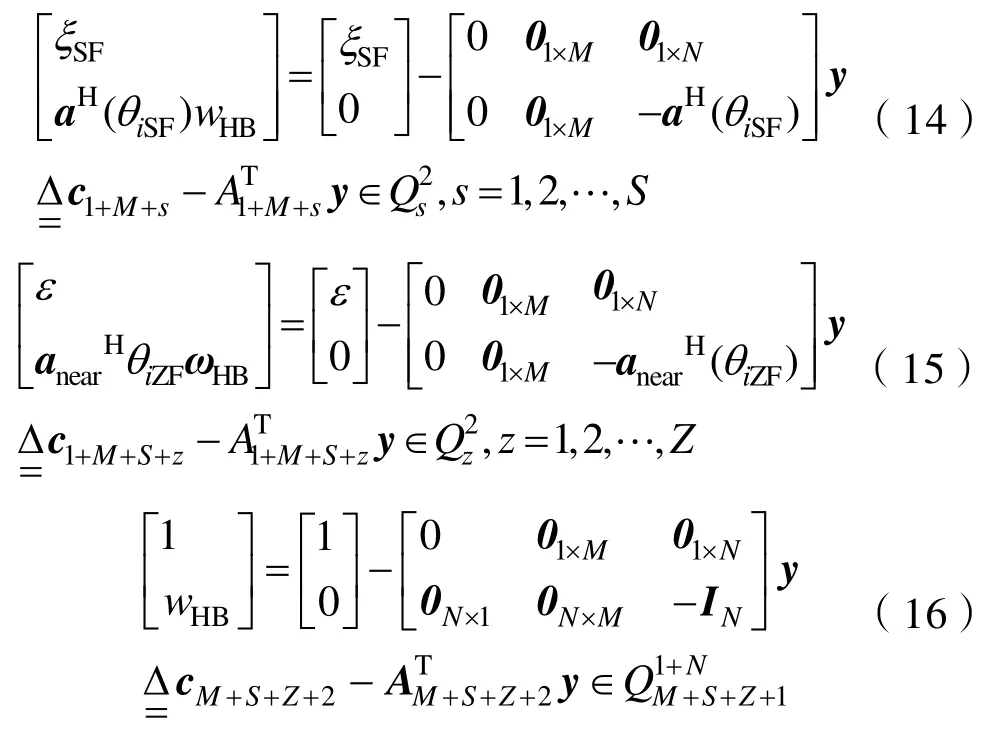
式中，IN是N維單位向量。

令

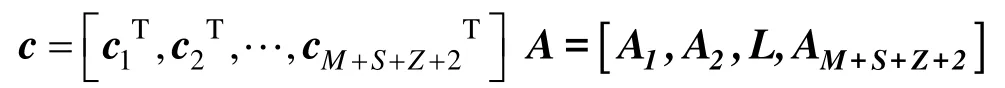
和ci，Ai(i=1,2,…,M+S+Z+2)由式（13）–（17）給出，則最后轉換為標準的二階錐問題

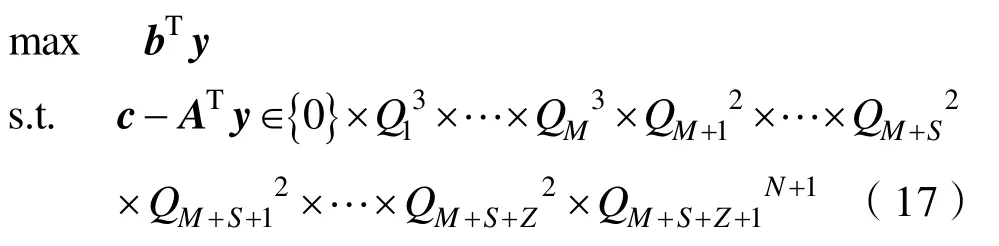
求解y得到其最優解，取第M+2～M+1+N個值即為所求陣列最優權值wHB。

2 仿真及實驗

在以下的仿真與實驗中，上述凸優化問題中的參數設置為：θMF=[-5?,5?]，θSF=[-90?,-8?]∪[8?,90?]，θZF=[65?,75?]，仿真中，ξSF=10-15/20，ξZF=10-60/20，θd=0?為期望信號來源方向。

文獻[9]中遠場條件下的波束響應如圖6所示，近場條件下的波束響應如圖7所示。

圖6 遠場條件下文獻[10]中算法的波束響應Fig.6 Beam response of algorithm in Reference [10]under far-field condition

圖 7 近場條件下文獻[10]中算法的波束響應Fig.7 Beam response of algorithm in Reference [10]under near-field condition

從圖 6及圖 7可以看出，文獻[9]中提到的方法在近場條件下，并沒有產生零陷的效果，而工程應用中通常情況下，本地自干擾源在近場范圍中，因此本文修改了凸優化方程中的導向矢量，引入向量，完成了近場補償后的波束形成器的設計。

本文經過近場補償后的遠場波束響應如圖 8所示，近場波束響應如圖9所示。

圖8 遠場條件下本文算法的波束響應Fig.8 Beam response of algorithm under far-field condition

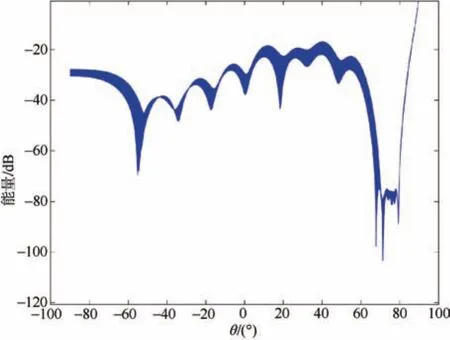
圖9 近場條件下本文算法的波束響應Fig.9 Beam response of algorithm under near-field condition

從圖8、圖9中可以看出，經過近場補償后的波束形成器能夠在遠場范圍處指向期望信號，并能夠在近場范圍中精準地抑制自干擾信號。為進一步證明本文方法的有效性，本文進行了水池實驗，實驗場景如圖10所示。

圖10 消聲水池實驗環境Fig.10 Experimental environment of anechoic pool

圖 11展示的是在無自干擾的情況下，用標準DOA估計方法估計的期望信號的方向，以便確定凸優化方程。圖12展示的是經過文獻[9]與本文方法的SSIC后殘余自干擾信號頻譜對比。

圖11 信道響應Fig.11 Channel response

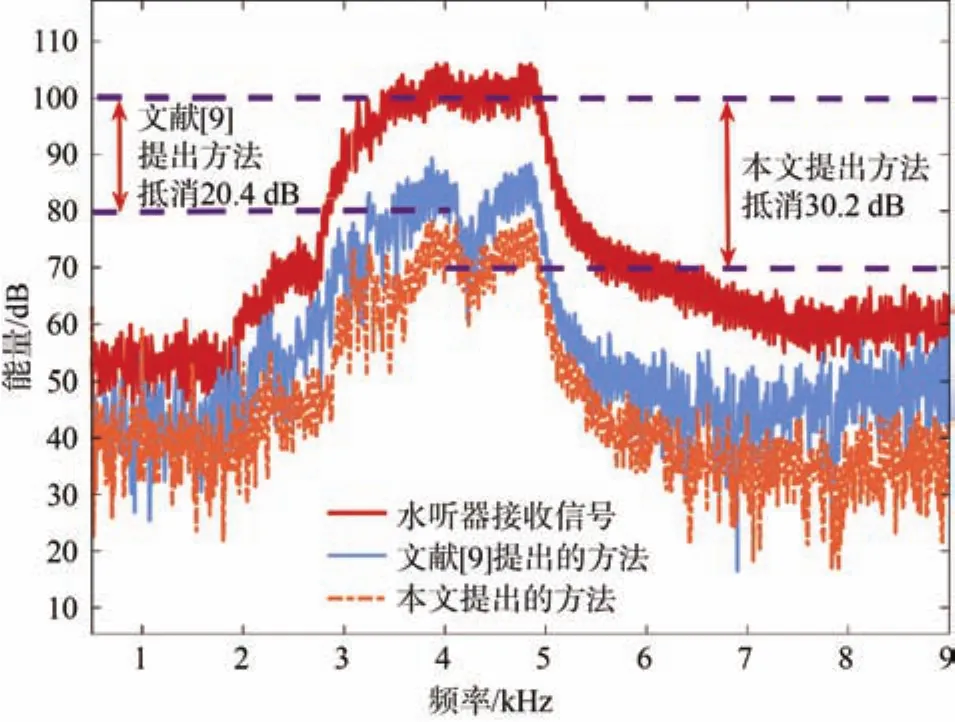
圖12 經過文獻[9]與本文方法的SSIC后殘余自干擾信號頻譜對比Fig.12 Spectrum comparison of residual self-interference signal after SSIC in Reference [9] and this method

從圖12可以看出，本文提出的SSIC方法相比于文獻[9]有著更好的SSIC效果，SSIC效果提升了9.8 dB并提升了IBFFD-UWAC系統總體SIC水平。

3 結束語

本文基于近場補償模型與已有研究結果，對近場條件下的帶內全雙工水聲通信系統的空間域自干擾抵消進行了仿真與分析，仿真結果表明近場效應對自干擾信號會有影響，導致SSIC效果未達到最優。本文提出的SSIC算法能夠解決近場效應帶來的問題。通過引入近場導向矢量并修改凸優化方程，完成了最優波束形成器的設計，獲得了更高的SSIC抵消效果，提高了IBFD-UWAC系統SIC上限，為后續空間域自干擾抵消提供理論基礎以及實驗基礎。