基于INS/DVL/GPS的UUV組合導航技術分析

呂志剛

（1.中國船舶集團有限公司第七一〇研究所，湖北 宜昌 443003；2.清江創新中心，湖北 武漢 430076）

0 引言

組合導航系統可為UUV長航時水下航行提供精確的姿態、航向、速度和位置信息，精確的導航能力是 UUV任務完成和安全回收的一項關鍵技術。但由于受總體尺寸、重量、功耗等條件限制，水下環境的特殊性及隱蔽性等諸多因素的影響，實現UUV水下高精度導航仍然很困難，水下組合導航仍然是UUV所面臨的主要技術挑戰之一。

目前，單一的導航方式由于自身的不足，如單一的慣性導航系統和 GPS導航，已無法滿足水下高精度的導航要求，而目前基于INS/DVL/GPS的水下組合導航方式為UUV通常采用的一種導航方式，可解決導航誤差隨時間積累的難題[1]，滿足UUV長航時水下航行的要求。

1 水下組合導航系統的結構和組成

水下組合導航系統一般由INS、DVL、GPS和深度計構成。深度計為可選擇的配置，下潛深度在300 m以內的UUV可以不配置深度計。配置了深度計的UUV導航精度可以進一步提升，特別是天向速度和高程信息精度可以大大提升。下潛深度遠大于300 m的UUV，一般要求配置深度計，以提高導航的精度[2-3]。水下組合導航原理簡圖見圖1。

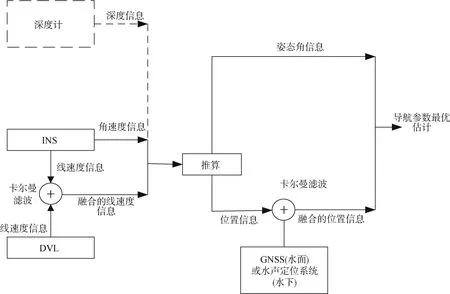
圖1 水下組合導航原理圖Fig.1 Schematic diagram of underwater integrated navigation

2 組合導航系統的關鍵技術

制約 INS與 DVL組合導航的因素有很多，DVL的測速精度和INS的姿態精度是影響組合導航精度的2個重要因素。通過DVL標定可降低INS與DVL之間的安裝偏差對DVL測速精度的影響，從而提高系統的導航精度。對準精度和對準速度是慣性導航系統進行初始對準時的 2項重要技術指標，初始對準精度影響慣性導航系統的性能，為了提高慣性導航系統的性能，需要通過高精度的初始對準技術來保證系統的初始信息精度，尤其是初始姿態精度。

2.1 DVL標定

DVL測量得到的是DVL在UUV坐標系下的速度，它通過INS的姿態轉換到導航坐標系下。在生產制造和安裝過程中，很難保證INS的UUV坐標系與DVL的UUV坐標系完全重合。因此，若不進行INS與DVL的安裝偏差進行標定，將產生一定的測速誤差，從而影響導航的定位精度。由于INS的精度在很大程度上由器件決定，因此，提高INS與 DVL組合導航精度的主要途徑在于提高DVL的測速精度。通過對DVL標度因數和INS與DVL之間安裝誤差的標定可提高INS、DVL組合導航精度，為了提高INS/DVL組合導航系統精度，國內外學者廣泛關注了INS與DVL安裝偏差的標定問題。最早的標定方法只考慮了 1個自由度，1989年，JOYCE提出了一種基于最小二乘的估計船載DVL航向安裝誤差的方法，該方法以GPS的速度作為參考來估計安裝偏差[4]。對于DVL標定，國內通常采用 GPS輔助下的標定方式，國內學者對DVL安裝偏差的在線估計也作了一定的研究，但是，由于水下航行器的機動性較小，也難以取得比較好的估計效果。

綜上所述，DVL測速誤差標定的難點在于水下航行器難以得到額外的速度、位置觀測，且水下航行器機動性較小，為實現目標定位帶來極大的難度。

2.2 INS初始對準

INS初始對準的目的是為了確定初始時刻的姿態矩陣。初始對準的精度對慣性導航系統的導航精度有著重要的影響，初始對準的時間在很大程度上決定了 UUV的快速反應能力，因此，對準精度和對準的快速性是初始對準最重要的2個指標。按不同的劃分標準可以把INS的初始對準分為靜基座對準和動基座對準。對于靜基座對準技術，研究成果已經比較成熟，而動基座一直都是慣性導航學術界關注的熱點。動基座對準包含2種情況：1）UUV受到機械振動、外界風力、浪涌等影響而引起的基座擾動；2）UUV在水面航行中進行初始對準。

一般來說，初始對準包括粗對準和精對準2大部分，粗對準過程是一個提供UUV坐標系和導航坐標系之間姿態矩陣初始值的過程。目前初始對準最常用的方法是慣性系粗對準法，該算法有一定的抗基座搖晃能力，適合于系泊狀態下的航行器或艦船的粗對準。精對準則是利用外部觀測量的信息，進一步得到UUV坐標系和導航坐標系之間姿態矩陣的精確值。典型的精對準方法有羅經法、DVL輔助下的UUV行進間羅經法、基于最優估計（常用卡爾曼濾波估計）的對準方法等。

3 導航系統算法

導航系統算法主要包括初始對準、DVL標定、純慣性導航算法、組合導航算法和校準算法。

3.1 初始對準算法

初始對準算法有很多種，除了少數先進的對準算法，大部分初始對準都包含粗對準和精對準2個過程，最合適AUV的是慣性系粗對準和卡爾曼精對準算法。

3.1.1 慣性系粗對準[5-7]

慣性系粗對準過程采用晃動基座對準方式解算INS的初始姿態，姿態矩陣方程為

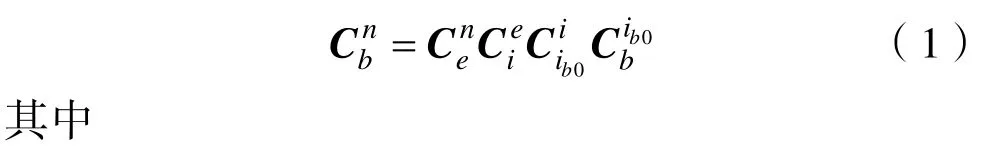
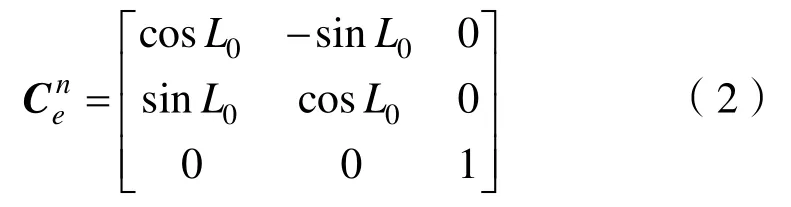
e系和n系的坐標轉換僅與大地維度信息有關，從e系到n系的變換矩陣為公式（2），其中L0為大地維度。

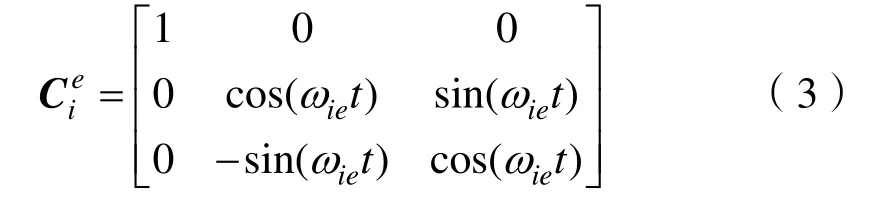
公式（3）為從i系和e系的轉換矩陣，即e系相對于i系的轉動，其中ieω為地球自轉角速度。

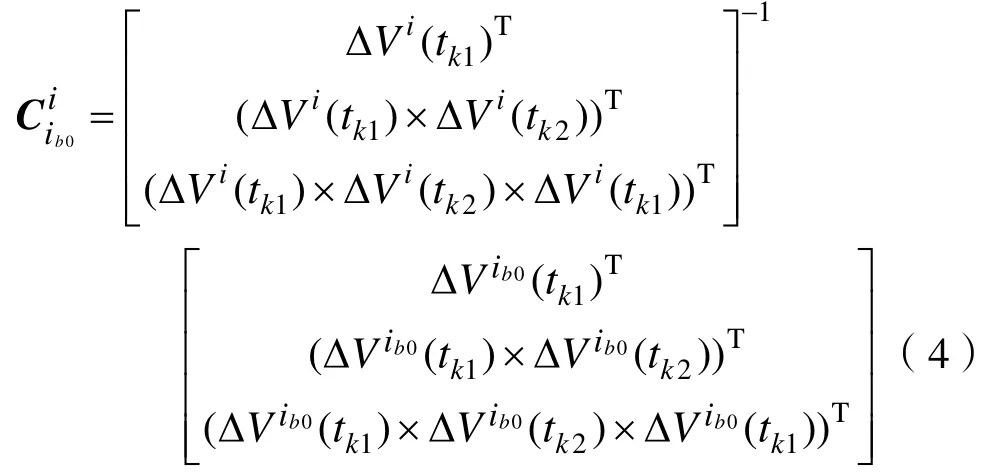
3.1.2 卡爾曼精對準

選用常用的卡爾曼模型，狀態變量選擇為如下的15維列向量：

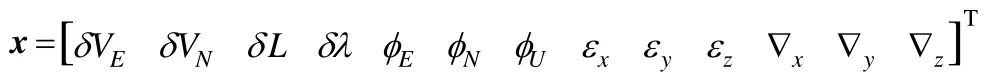
式中：δVE、δVN為速度誤差；δL、δλ為緯度、經度誤差；Eφ，Nφ，Uφ為姿態誤差；xε，yε，zε為陀螺漂移；?x，?y，?z為加速度計零偏。狀態變量對應的高斯白噪聲選為

卡爾曼模型中的狀態轉移矩陣F如下：

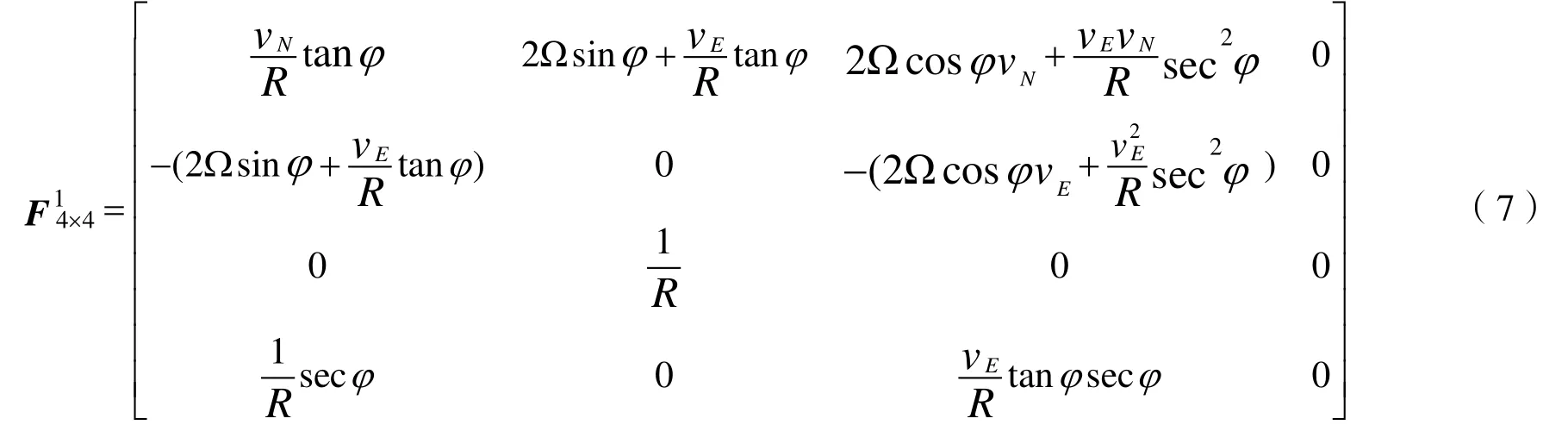
卡爾曼模型中的X的噪聲W前面的矩陣

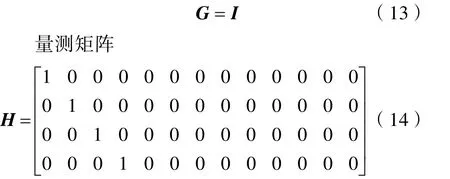
模型中量測量Z對應的噪聲記為V，它是高斯白噪聲。

模型中量測方程

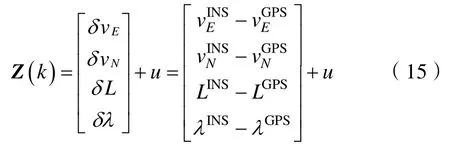
以上就是卡爾曼精對準的全部計算公式，但精對準結束時刻，應該用卡爾曼濾波估計的誤差修正純慣性的計算結果，而不是直接用衛星定位裝置或DVL的量測信息進行修正。因為前者不含噪聲，精度較高，后者包含了一定的噪聲，修正的效果不好。

3.2 純慣性解算算法

純慣性解算算法是利用慣性測量單元（IMU）的測量數據不斷地推算UUV當前的姿態、速度和位置信息，包括姿態更新算法和速度位置更新算法2部分。

純慣性解算算法的流程圖見圖2。

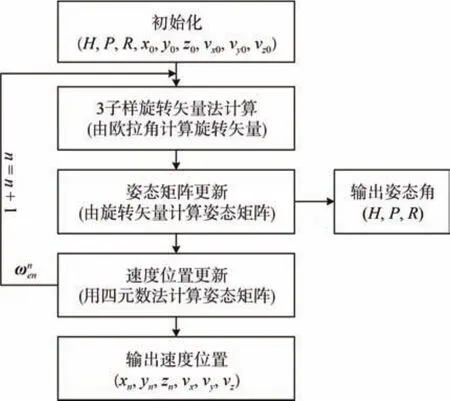
圖 2 純慣性算法流程圖Fig.2 Flow chart of pure inertial algorithm

3.3 組合導航算法

組合導航算法是利用 DVL的速度信息進行組合導航，主要有線性卡爾曼濾波、非線性卡爾曼濾波與粒子濾波等，最常用的就是線性卡爾曼濾波法。

組合導航過程采用 Kalman濾波計算濾波模型。估算出誤差以后，用純慣性結果減去誤差得到組合導航的結果。

在每個導航周期進行狀態轉移矩陣F的離散化計算，轉移矩陣Φk,k-1計算如下[8-10]：

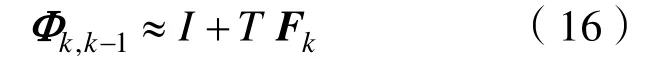
式中，T為導航周期。

當接收到有效的接收機信息時，進行 Kalman濾波計算，計算過程分為5步：

式中：為當前濾波周期的實時狀態估計值；k/k-1為上一濾波周期對當前濾波周期的狀態預測值；Kk為當前濾波周期的濾波增益陣；Pk/k-1為上一濾波周期對當前濾波周期的預測誤差估計的協方差陣；Pk為當前濾波周期的實時誤差估計協方差陣；Qk為系統噪聲方差陣；Rk為量測噪聲方差陣。

量測方程為

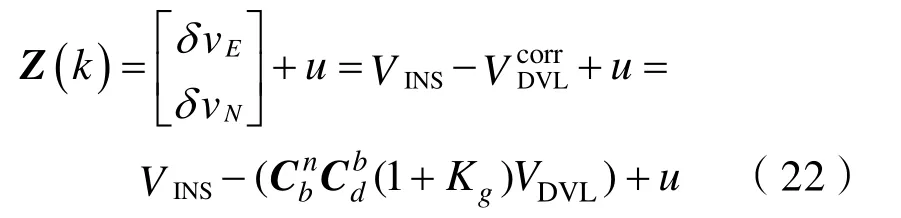
卡爾曼濾波算法流程如圖3所示。

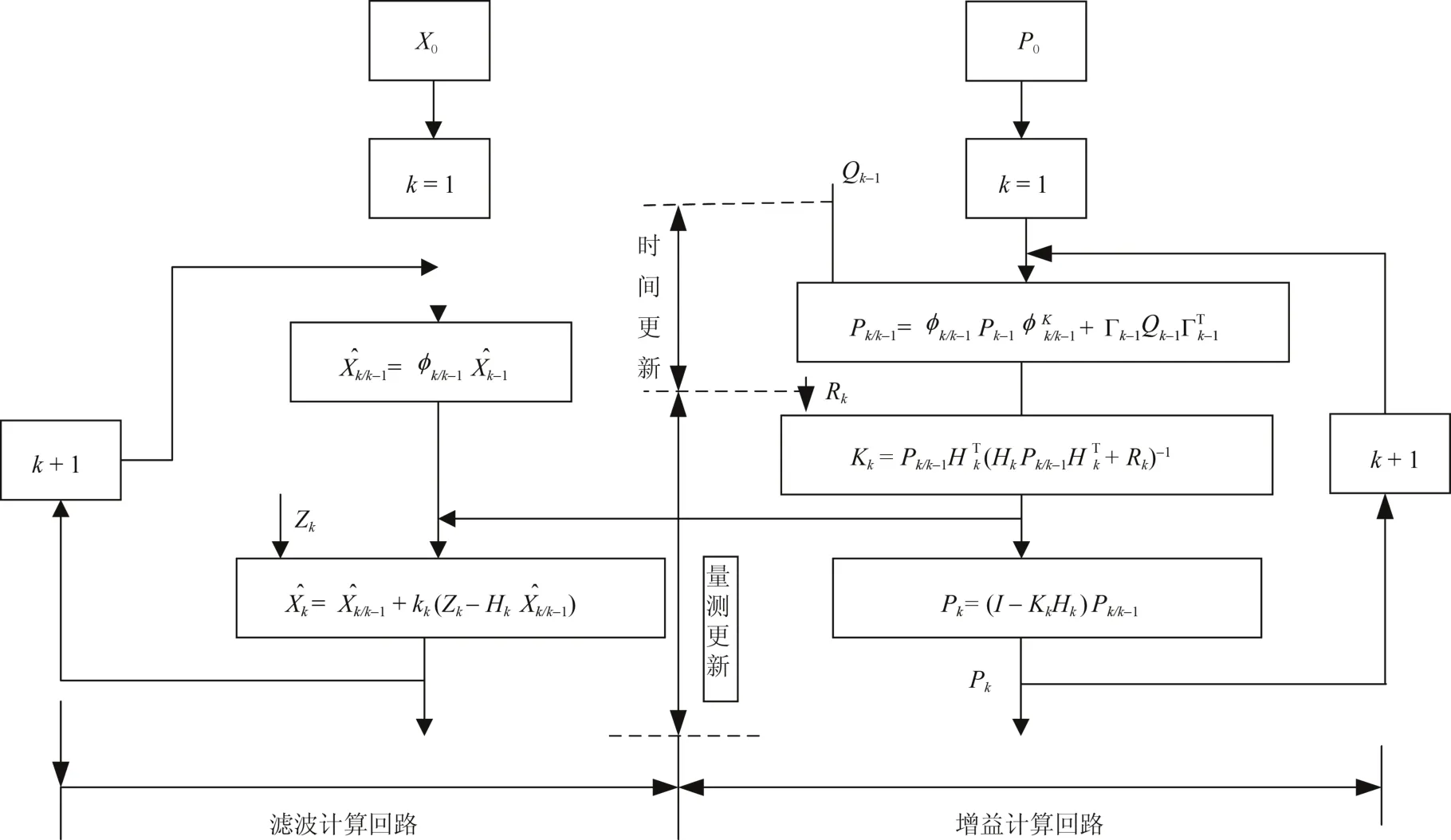
圖 3 卡爾曼濾波算法流程圖Fig.3 Flow chart of Kalman filtering algorithm

3.4 DVL標定算法

由于DVL與INS之間有安裝誤差，導致DVL測量的速度與INS需要的速度值不一致，需要標定出安裝誤差進行補償才能夠提高組合導航的精度。最常用的標定算法是兩點法，利用起點和終點處的GPS信息進行航向角安裝誤差與標度因子這2個變量的標定。

3.4.1 基于卡爾曼濾波的標定方法

DVL輸出的測量速度VDVL與INS組合導航所需要的速度vb之間的關系為[11]

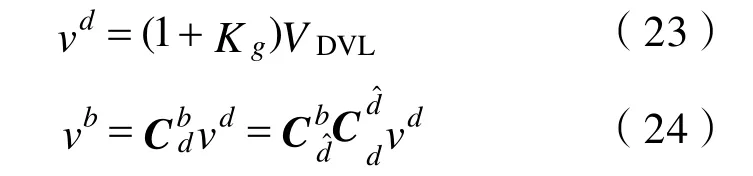
式中：VDVL是DVL輸出的自身坐標系下的原始速度數據；Kg是標度因數。

姿態矩陣為

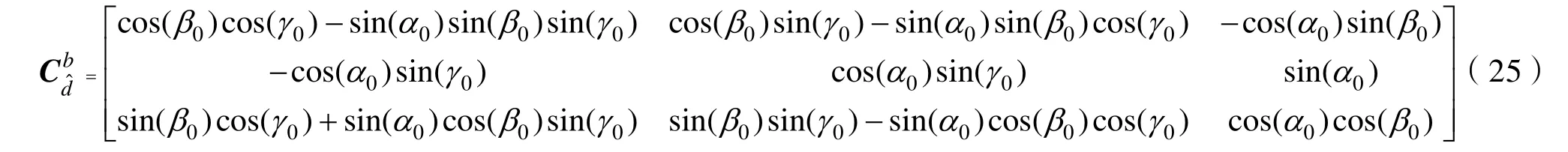
式中，α、β、γ分別為俯仰、橫滾、航向安裝誤差角。

標定算法數據傳遞關系圖和標定算法流程圖分別如圖4和圖5所示。圖5中加入了反饋，這樣即使設定的初始值偏離真實值很遠，幾步迭代以后也可以保證算法收斂。

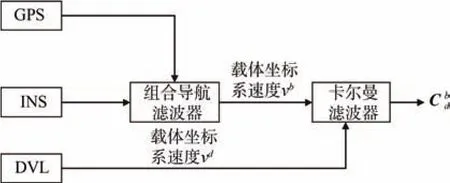
圖 4 標定算法數據傳遞關系圖Fig.4 Data transmission relation diagram of calibration algorithm

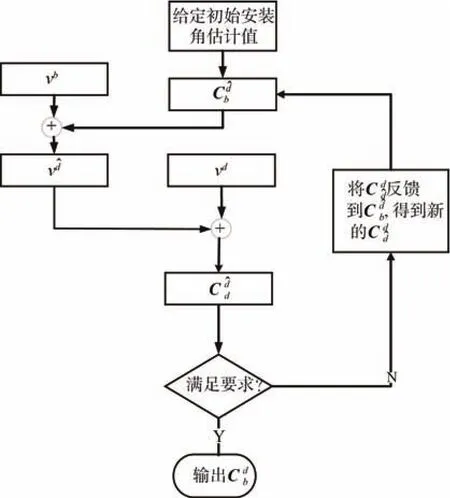
圖 5 標定算法流程圖Fig.5 Flow chart of calibration algorithm

標定完成得到標定參數以后便可以將VDVL轉換為vn進行組合導航：

還可以改進卡爾曼模型，把速度標度因數Kg也包含進去，一起進行卡爾曼濾波估算。可以自行采用類似的方法進行推導。

3.4.2 基于航程起點終點位置信息的標定方法

利用一段直線航程（一般選為6 km或7 km為1個標準航程）的起點與終點 GPS信息可以進行DVL的標定，這種方式常稱為兩點標定法。此方法只需要 UUV在航程起點和終點處位于水面即可，其余時間UUV都可以在水下航行，標定方式更利于UUV的隱蔽。

這種標定方法的原理和計算公式十分簡單，就是計算組合導航推算的直線航路、GPS起點與終點構成的實際直線航路之間的夾角和長度比值。

3.5 校準算法

校準是指當 UUV下潛前或上浮后接收 GPS（常用GPS和北斗等）的位置信息進行INS誤差的估算與補償。其本質就是基于 GPS位置信息的組合導航算法，只要對組合導航算法稍加修改就可以實現校準算法。

1）純慣性導航時的校準。

衛星定位裝置僅位置信息有效時，就用位置誤差信息作為觀測進行校準；衛星定位裝置僅速度信息有效時，就用速度誤差作為觀測量進行校準；衛星定位裝置的位置信息和速度信息同時有效時，就用位置誤差信息和速度誤差同時作為觀測量進行校準。

2）組合導航時的校準。

不管 GPS的速度信息是否有效，都不用其速度信息，只用 GPS的位置信息得到的位置誤差作為觀測量進行校準。為了解決DVL組合模式切換到 GPS組合模式時卡爾曼濾波器的振蕩甚至發散的問題，也可以采用校準時重啟卡爾曼濾波器或替換法等技巧。當然，這種方法也會帶來一些弊端，重啟卡爾曼濾波器的缺點是卡爾曼重新收斂一般需要幾分鐘的時間；替換法的缺點是只對位置進行了校準，速度和姿態沒有得到校準，組合導航精度不夠高。

校準方式不限于如上2種，對于大深度UUV，位置信息還可能來自水聲定位系統，考慮延時補償后對大深度AUV進行校準。同時，還應該建立重力加速度模型考慮不同深度下重力加速度值的變化。校準算法的本質就是卡爾曼組合導航，所以校準算法的公式參考組合導航算法即可。

4 結束語

水下組合導航是UUV完成長航時水下自主航行和任務的技術保障和基礎，而組合導航技術是提高 UUV導航精度的主要手段。本文章針對基于SINS/DVL/GPS的水下組合導航技術進行了分析，闡述了水下組合導航系統的關鍵技術，隨后對初始對準算法、純慣性解算算法、DVL標定算法和校準算法進行了詳細論述，對水下組合導航具有一定的參考價值。