三角形穩定性的數學本質與教法探索

江蘇如皋市李漁小學（226500） 任曦

如何理解三角形具有穩定性這一性質？通過查閱詞典，筆者發現三角形穩定性中的“穩定”即“不易發生形變”的意思，與“松動”“易變形”的意思相對。

一、“三角形穩定性”的本質

1979年，美國兩位學者發表了題為《圖形的穩定性》的數學論文，對具有穩定性的幾何圖形做了系統的梳理和詳細介紹：

由一個頂點O引出兩條邊后能得到一個幾何角，如果邊可以隨意旋轉，那么角O的大小、形狀就會隨之變化，這時圖形不具備穩定性。但如果在這兩條邊上各找一個點，通過一條線段將這兩個點（端點）的距離固定（如圖1），也就是將PQ的長度固定，那么角O的開口大小就被兩個端點的距離“固定”了。此時，幾何圖形OPQ就是一個三角形，角O的穩定性自然轉移為三角形的穩定性。

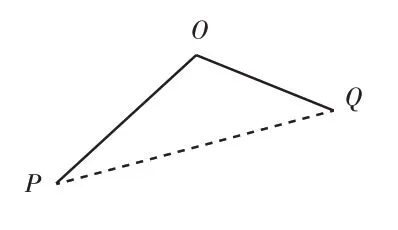
圖1

如圖2，在任意△ABC中，只要保持三邊長度不變，那么任意一條邊的長度都可視為連接對應角的兩條邊的端點的距離，那么三角形三個端點間的距離就不變。于是三角形就不會發生形變，所以三角形具有穩定性。

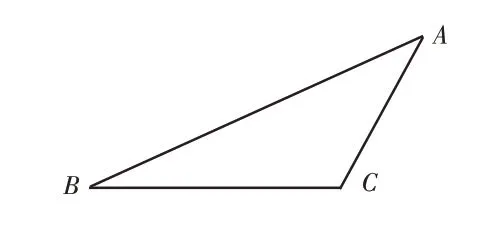
圖2

還有一篇關于平面圖形穩定性的論文，進一步從幾何公式的角度闡釋了如何判斷圖形的穩定性：由拉曼圖組成的幾何圖形才具有穩定性。拉曼圖的定義為“在平面內具有穩定性的圖形，其邊和頂點的數量必須滿足這樣的數量關系，若頂點數為n，那么邊數必為2n-3；若n≥3，那么任意兩邊的‘斷點’必須連接起來”。照此定義，任意一個幾何多邊形，只要充分連線，都可以轉化為拉曼圖。

通過計算可知，三角形的頂點數和邊數符合拉曼圖的定義，三角形是最簡單的拉曼圖。四邊形要獲得幾何穩定性，根據拉曼圖原理，其必須建立4×2-3=5（條）線段。除了四邊形所需的4條線段，為了連接不相鄰的頂點，還要連接對角線，這樣就將四邊形分割成兩個三角形。同理，五邊形、六邊形也是一樣的操作方式。（如圖3）

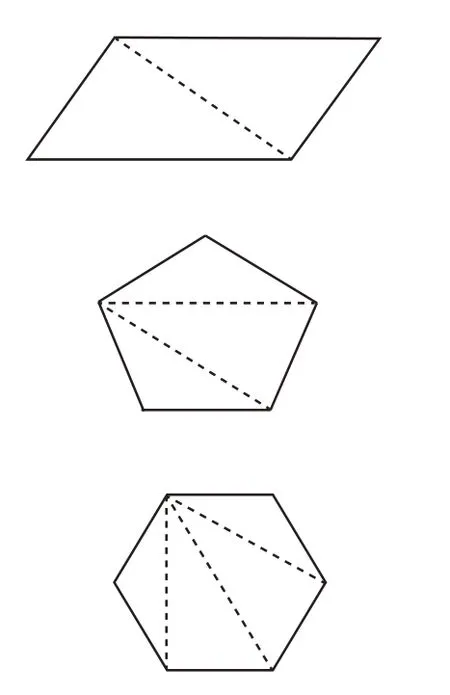
圖3

從理論根源上找到三角形具有穩定性的奧秘，才是對三角形穩定性的最深刻認識。

二、與相關知識的聯系

“三角形的穩定性”在人教版教材中被編排在第八冊第三章第二課時，是學生學完三角形所有概念后的學習內容。在這之前，學生已經對基本的幾何圖形及其運動形式有所了解，在第七冊中又學習了四邊形的易變性，為后續學習三角形的穩定性積累了經驗。

但人教版教材在編排“梯形”的內容時，用梯子等穩固的物品引入梯形的概念就不妥當，容易傳遞梯形具有穩定性的錯誤信號，誤導學生。“三角形的穩定性”是一個重要的性質，它是學生將來在中學學習全等三角形的判斷的理論基礎。雖然全等三角形的知識在小學不作學習要求，但是小學數學教師要具有前瞻性，合理地進行知識的滲透。

據史料記載，人類歷史上首次提出并證明全等三角形的人是古希臘人泰勒斯。他是第一個應用了全等三角形判定定理的人。三百年后，歐幾里得對全等概念做了系統闡述，其中有一條被稱為萬能判定定理的法則——彼此重合的物體是全等的。他還給出了全等三角形的三種判定方法：“角邊角”“邊邊邊”“角角邊”。其中，“邊邊邊”的判定方法與三角形的穩定性不謀而合，即如果三角形三邊長度固定，那么三角形的形狀也唯一確定。三角形穩定性的用途十分廣泛，涉及地理、建筑、外交、軍事、政治等領域。例如，要想形成穩定的外交關系，就要努力建立“三足鼎立，互為犄角”的外交關系。反之，要破壞穩定，則要破壞這種三角結構。

到了初中，學生的理論水平大幅提高，學生就會思考：為什么所有的幾何圖形中只有三角形存在全等的概念，而其他圖形則沒有這個提法？從而發現，因為三角形具有穩定性，而三角形穩定性的來源恰好可以作為全等的判定依據。所謂全等，實際上就是對三角形形狀、大小的唯一性做出確認，在這個三角形的形體唯一性被確認后，按照這種“尺碼”打造的任何三角形都是這個三角形的復制品，它們統統全等。也就是說，任意一個三角形的形態都是獨一無二的，凡是相同者必然有符合促成其穩定性的全部特征。

三、教學設計思路

三角形的穩定性是三角形的本質屬性，是客觀存在的幾何特征。教學目標可以確立為“探究三角形三邊長度對三角形形狀結構穩定性的影響”。要順利完成教學目標，不妨讓學生經歷觀察、猜想、驗證、應用等數學過程，逐漸體會三角形的穩定性。

【第一環節】理解穩定性的概念

人教版教材對穩定性沒有出具合理的權威解釋，且編排的“梯形”內容還從穩固的實物中提煉出不穩定的梯形，這容易對學生造成負遷移。因此，在課堂引入階段提出要求：請你解釋什么是幾何意義上的“穩定”，試著舉出幾個例子。目的是讓學生領悟這里的“穩定”是指圖形的形狀、大小不變，為之后的研究扎根。

這一環節中，學生需要結合自身經驗，先回顧什么是物體的穩定，再通過操作研究出三角形一邊長短可以決定其對角的開口大小，探明三角形三邊長短決定三角形的形狀、大小，從而提出猜想。教師緊接著從角引入穩定性，提出類似“用兩根長度固定的木棒做試驗，想一想，如何添加學具才能制作一個大小不變的角？”的問題，啟發學生想到用第三根木棒來固定，構成三角形。

【第二環節】學生觀察和操作

通過“如果第三根木棒的長度有變化，角和組成的圖形會發生什么變化？四人一組，交流和歸納自己的發現”這樣的任務，讓學生體會三角形三邊長短決定了其形狀大小，并聯系前面提到的穩定概念，提出三角形具有穩定性的猜想。此外，可以讓學生完成“用木棒拼擺各種不同的多邊形，看看是否可以隨意變形”“要使其具有穩定性，可以如何操作”等任務，讓學生體驗到三角形才是最穩定的基本幾何圖形。

學生觀察圖形的變化情況，發現三角形邊、角、形三者之間的制約關系，發表觀點并討論。

【第三環節】驗證猜想，得出結論

經過上一環節，學生已經明確三角形的形狀由三邊長短決定，本環節就只待證明。考慮到三角形的穩定性與全等三角形的關系，這一環節中教師應鼓勵學生尋找更多成就了三角形的穩定性的因素。

【第四環節】三角形穩定性的應用

由于學生個體間存在差異，應用環節應分層設計任務，兼顧全體學生。針對后進生，設計諸如“尋找具有三角形穩定結構的物品”的活動；針對中等生，則設計諸如“設計具有三角形穩定性的物品并說明設計思路”的活動；針對優等生，則可將三角形的穩定性從幾何領域引申到外交策略，實現學科融合。

例如，美國和朝鮮關系緊張，中國如何在保證自身安全的情況下，妥善處理與美國和朝鮮的關系？教師讓學生分小組查閱資料，利用三角形的穩定性，想一想作為一名外交官，應如何處理與美國和朝鮮之間的外交關系。

三角形之所以具有穩定性是因為三邊、三角相互制約，形成三足鼎立、互為犄角的局面，三邊三角互相牽制。也就是說，三角形的角、邊形成了“一榮俱榮，一損俱損”的聯盟關系。以此類推，生活中凡是具有三方勢力相互制約的情形，都可以形成穩定結構，比如三角關系、三腳架、三國外交等，這些都是對三角形穩定性的升華和拓展。

作業的層次可由學生自主選擇，也可由教師根據課堂情況靈活處理，比如給出兩個任務，由學生任選其一。因為學生的任務不相同，最好能留到課后完成，然后課上匯報交流。

在教學“三角形的穩定性”時，所有的數學活動既要符合學生的心理特征，又要契合數學本質規律，讓學生的觀察、操作等系列數學活動都能直擊數學知識本質，從而深刻揭示三角形具有穩定性。

本節課的教學能讓學生擁有更自由的探究空間。學完后，學生在知識方面有了很大的收獲，包括三角形穩定性之外的全等，及決定三角形穩定性的因素等。在個人能力方面，既有獨立思考，又有合作探究，在交流分享中學生的協作意識和交流意識得到提升。

值得強調的是，教學有法但無定法，教師需要根據實際情況，靈活選擇適合自己和學生的教學方法。