搭建思維平臺促進有序思考
浙江淳安縣汾口鎮龍川小學(311719) 姜素貞
新修訂的人教版教材大力開發了有序思考的強大功能,表1是修訂前后的教材在有序思考內容上的對比。
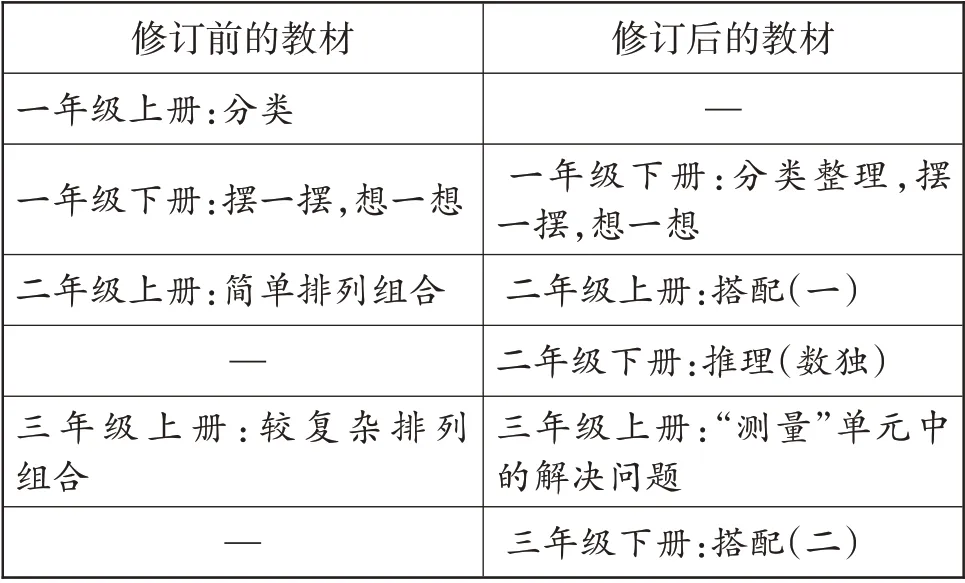
表1 修訂前后的教材內容上對比
通過對比,可以找出兩點不同:關于有序思考的課程明顯增加;新版教材專門列出一個關于有序思考的“解決問題”模塊。因此,如何將有序思考植入問題中,切實提高學生有序思考的能力呢?對此,筆者選取了人教版教材第五冊“測量”一章中新設的“解決問題”模塊來“破題”。
一、創設情境,搭建支架
技能不是一朝一夕可以練就的,需要日復一日地苦練。尤其是低年級學生,他們以形象思維為主,對有序思考的認知必須借助直觀演示,然后抽象出有序思考的過程。這就需要教師創設巧妙的情境,使有序思考具象化、可操作化。
【案例1】
師:我們已經知道,計量較重的物品時,應以“噸”作單位。現在我們就一起來解決有關“噸”的問題。(出示圖1)

圖1
生1:用載質量為2噸的貨車來運,需要運4次。
師:再仔細讀題。假設你是運輸公司的老板,你能設計一個讓兩輛車的司機都能接到派單的派車方案嗎?
生2:我想到一種方案,可以讓兩個貨車司機都能接到任務,那就是用載質量為3噸的貨車運2次,還剩2噸煤,就用載質量為2噸的貨車運1次。
師:你確定這是最佳方案嗎?
生2:確定。
教師列出表格(如表2)。

表2 運煤方案
師:看來,這道題對你們而言是小菜一碟。現在老師變換一下數據,你們試著解一解這道題。(出示圖2)

圖2
師:要求不變,請列出所有方案。
【反思】教師大幅改動數據,提高難度,主要出于兩點考慮:(1)尊重教材的原型問題“如何派車能恰好運完8噸煤”,這其中的關鍵詞“恰好”,就已經排除了不能完成任務和浪費貨運資源的情況,且“8噸”這一數據較小,解決時用不上有序思考;(2)教材的例題只是一個引言,引出基本的數量關系,之后的數據改動才是真章,因為數據一旦變大,學生就無法憑經驗和直覺看出答案,有序思考就應運而生,學生在一一排查、手忙腳亂時,自然會設法尋找捷徑——有序思考。其實,創設情境本身就是為學生的思維發展“搭梯子”。
二、對比體驗,優化程序
通過“搭梯子”,學生感悟到有序思考的先進性。要讓學生真正理解、掌握、運用有序思考,教師還需設計對比分析環節,幫助學生逐步構建起有序思考的數學模型,并優化模型結構。
【案例2】
出示生1的方案(如表3)。

表3 運煤方案
師:誰來評價一下這位同學的方案?
生2:這位同學沒有列出完整的方案。
師:沒錯,那么如何才能列出所有方案?
生2:必須按照某種順序進行思考,一一列舉,這樣才能不重復、不遺漏。
教師出示生2的方案(如表4)。
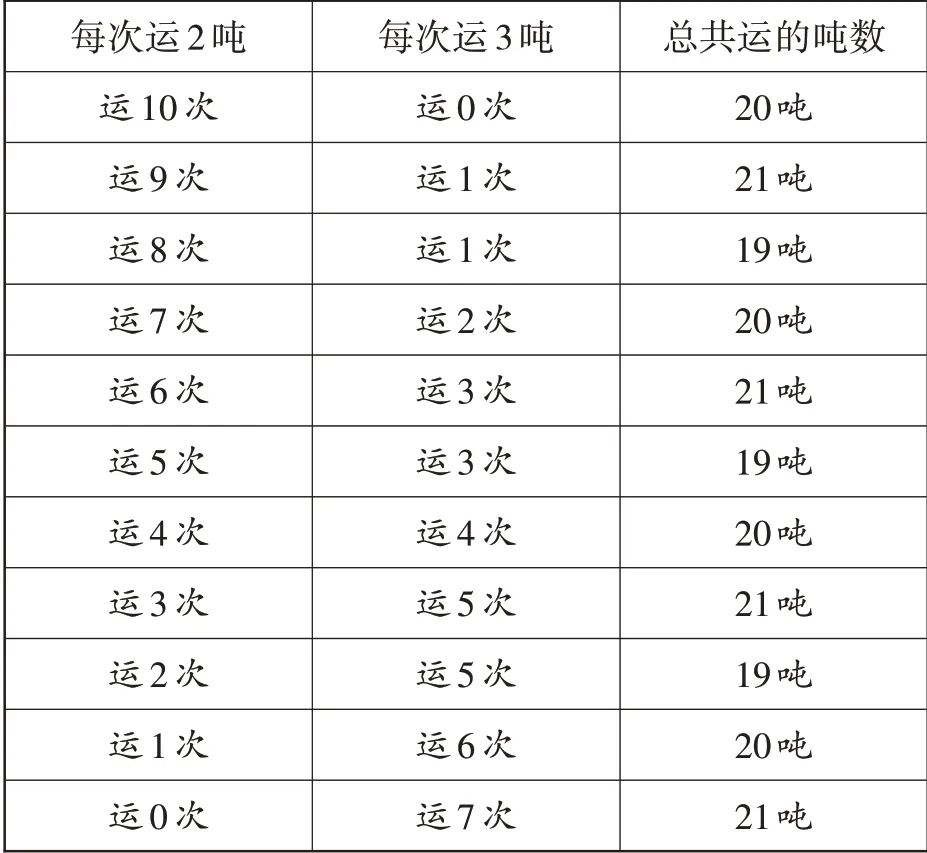
表4 運煤方案
師:如果說生1的思考是沒有條理的,那么生2的思考過程含有某種順序嗎?
(其他學生都表示“有”)
師:從第一列的數據就可以看出有順序,從10次到0次,一個不漏,那第二列數據是怎么來的?
生2:計算所得。
師:能試著舉例揭示這些數據的含義以及運算過程嗎?
生2:載質量為2噸的車運輸10次,總共運了20噸,因此就不需要載質量為3噸的車去運,即運0次;載質量為2噸的車運輸9次,已經運了18噸煤,余下的2噸就得讓載質量為3噸的車單獨運送1次,但是為了滿足“裝滿”的硬性規定,因此裝3噸煤,總共運21噸……
師:原來如此,只要列好了第一列的數據,就可以推算出第二列的數據,根據第一列的趟次預設,推算出已運送量和剩余量,然后將剩余量交由載質量為3噸的車來運,看看需要幾次。
師:對于這種思路,其他同學有什么想法嗎?
生3:老師,我認為有些數據沒必要列出,比如寫到第二行,當用載質量為2噸的車運9次后,就可以預判運送總量不是20噸,后面的數據沒必要寫。
出示生3的方案(如表5)。
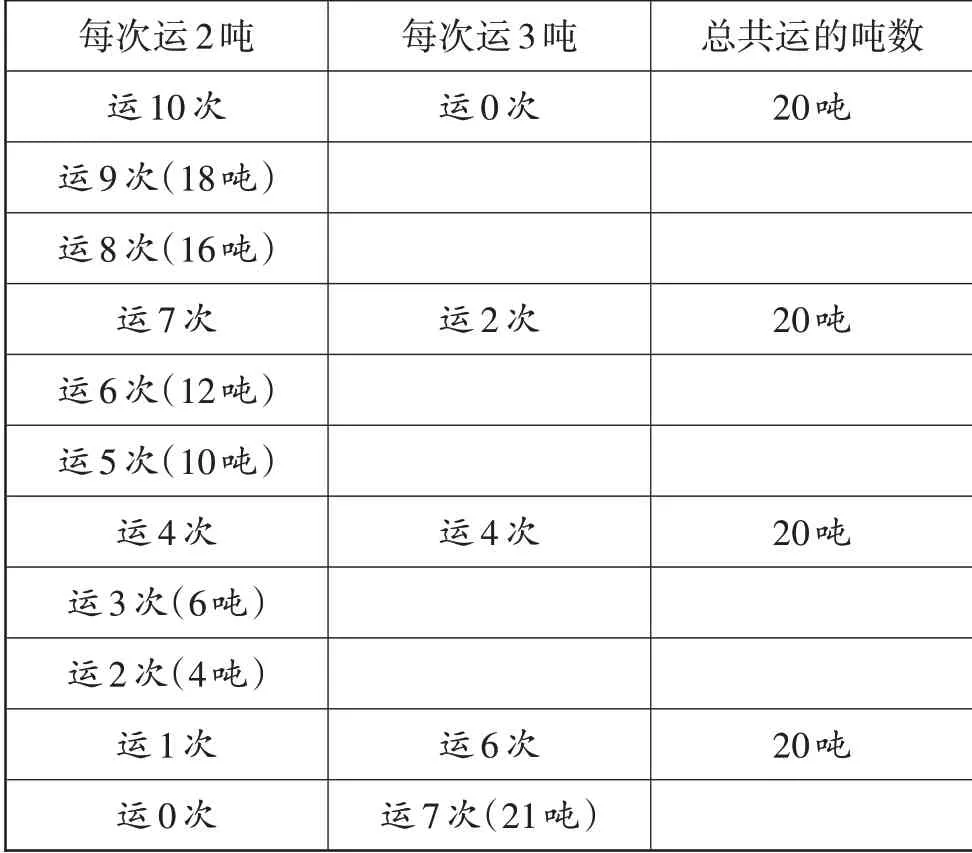
表5 運煤方案
師:對比生2和生3的思路,說說你的看法。
生4:其實他們的思路是一樣的,只是生3列出的表格更簡潔。
師:說明生3排除了大量方案,這樣會不會造成遺漏呢?
生5:這倒不必多慮,因為運用了制勝法寶——有序思考。
師:你青睞哪種方法?說說你的理由。
生6:當然是生3的方法,簡潔有力。
生7:既然有些數據不需要寫出來,那么還可以將表格再縮減一些。
出示生7的方案(如表6)。
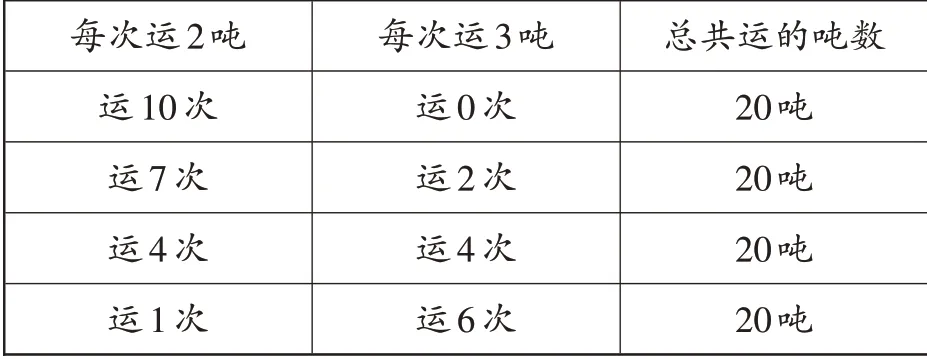
表6 運煤方案
【反思】這一教學環節才是本課的精華,在對比中展現有序思考的先進性,同時積累有序思考的經驗,不斷優化有序思考的程序。首次對比,目的在于彰顯有序思考的必要性,從只寫出2種方案到列舉全部方案,全靠有序思考打底;第二次對比則是為了排除不必要計算,已知載質量為2噸的車的運輸次數后,需要計算出載質量為3噸的車的運輸次數,只要熟記乘法口訣,就可以心算出結果,避免計算書寫,直接跳過不可能方案,從較大數算起,再加上有序思考加持,那么表格就會變得簡潔。
三、小結梳理,促進升華
從某種程度來說,大道至簡,思維的最高境界就是簡約。數學教學中,一種思維方式的滲透絕不會只在一節課內完成,而是通過長期的思維訓練來顯現數學本質,通過反思和回溯思維過程,促進學生思維的提升。
【案例3】
師:現在回看生7的表格,結合題意,你有什么新的收獲?小組討論。
生1:既然要滿足“用兩輛車運煤”的條件,那可以將表格再縮減(如表7)。

表7 運煤方案
師:這類題可以借助有序思考,列舉所有可能。其實所有的情況都可以用一個算式來表示,你知道是哪個算式嗎?
生2:3×()+2×()=20。
師:沒錯,其實所有情況都包含在一個算式里,只要滿足這個算式的情況都可行。另外,進行有序思考時,也需要從較大數據開始考慮。
【反思】現在提出“公倍數”這一概念為時尚早,但是可以提前滲透。事實也證明,這樣的滲透可以加速學生對有序思考的掌握。盡管算式“3×()+2×()=20”是一個拓展內容,但在學生建立有序思考的參考模型時發揮著巨大作用。首先,用算式構建有序思考的模型,便于學生找出數量關系;其次,對學生來說,越簡單的內容越好吸收,算式無疑是簡潔有力的模型。
總之,關于小學生有序思考能力的培養是一項艱巨的任務,教師應積極創造條件,在日常教學中滲透有序思考的內容,讓學生學會運用有序思考解決問題。

