不同形狀破片對945鋼靶的侵徹性能的影響規律分析
張 霄,李德聰
(中國艦船研究設計中心,湖北 武漢 430064)
0 引 言
目前反艦導彈大多采用半穿甲戰斗部,可穿透艦船舷側外板,進入艦船內部使其爆炸。一般而言,戰斗部殼體的質量在戰斗部總質量中的占比可達60%~65%,爆炸之后會產生大量高速運動的破片(初速度最高能超過2 000 m/s)[1-2],這些破片形狀各異,毀傷威力極大,對于船上的重要艙室而言,需在其四周艙壁處設置裝甲防護結構,以保證艙室內人員和設備的安全。
艦船裝甲防護結構一般根據防護等級要求設計。不同防護等級規定了所要防御破片的質量和速度要求,但未對破片形狀作統一的規定,對不同形狀破片的侵徹性能的分析缺乏量化的對比數據,給裝甲防護結構設計及其抗侵徹性能的橫向對比帶來了很大影響。苗春壯等[3]針對不同形狀破片的破壞威力,通過分析不同形狀預控破片的毀傷情況,認為正六邊形破片的預控效果最好,沒有產生相互粘連的破片,菱形破片存在少量雙破片粘連,正方形破片和三角形破片存在多破片粘連;通過對破片侵徹鋼靶進行仿真計算,得出在初速和質量相同的情況下,不同截面形狀破片的殺傷威力由強到弱為正六邊形、正方形、菱形和三角形。吳曉鳳等[4]認為孔徑大小通常可作為破片毀傷性能評估的標準之一,孔徑較大可在一定程度上視為殺傷能力較強。因此,就孔徑大小而言,立方體形破片的破孔能力最強,圓柱形破片次之,球形破片最弱。艦船裝甲結構抗高速破片侵徹的過程是一個復雜的強非線性動態毀傷過程,具有穿甲時間短和載荷強度大的特點[5-11]。目前常用的裝甲結構抗破片侵徹分析方法主要有試驗法、經驗法和數值仿真法,其中數值仿真法不僅成本較低,而且能較好地模擬破片穿甲過程中結構毀傷的細節,并能給出準確的破片剩余速度等關鍵數據,因此得到了廣泛應用。本文采用ANSYS/LS-DYNA軟件對球形、圓柱形(長徑比為1.5)和立方體形等3種形狀破片侵徹艦船945鋼均質裝甲結構的過程進行數值模擬,通過對比不同形狀破片的彈道極限速度,獲取其對945鋼均質靶板的侵徹性能的影響規律,以期為艦船裝甲防護結構設計提供參考。
1 破片侵徹靶板有限元模型
1.1 仿真對象
破片:材料為艦用945鋼;質量為3.98 g;形狀分別為立方體形、圓柱形(長徑比為1.5)和球形。
靶板:材料為艦用945鋼;形狀為正方形;尺寸為240 mm×240 mm×8 mm;四周固支。
1.2 材料模型
在破片高速侵徹鋼質靶板過程中,破片與靶板均存在明顯的大變形和毀傷現象,因此在仿真計算中破片和靶板均采用Johnson-Cook材料模型(簡稱為J-C模型)模擬,該模型考慮了材料的應變率和溫度效應,能很好地表征材料在侵徹過程中的塑性大變形和損傷破壞等力學行為,適于在金屬由準靜態轉變為大應變、高應變率和高溫狀態的情況下應用。J-C本構模型的表達式為
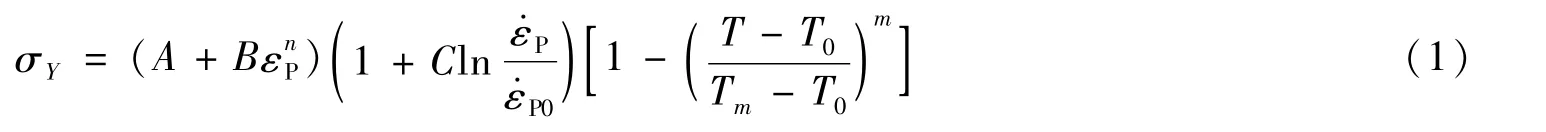
式(1)中,A為靜態屈服極限;B為應變硬化模量;εP為塑性應變;為塑性應變率;T為溫度;n為應變硬化指數;C為應變率系數;為參考應變率;Tm為材料的熔點;T0為參考溫度;m為熱軟化系數。
破片和靶板的材料均為艦用945鋼,其模型參數的取值參照文獻[12],具體見表1,其中:E為彈性模量;υ為泊松比;ρ為密度。

表1 945鋼的主要力學性能和J-C模型參數
1.3 數值仿真方法的準確性驗證
為檢驗數值仿真方法的準確性,以侯海量等[13]開展的侵徹試驗為例進行仿真模擬。該試驗中的破片和靶板的材料均采用艦用945鋼,通過將仿真結果與文獻[13]中的試驗數據相對比,檢驗數值仿真方法的準確性。試驗中采用FSP形破片侵徹正方形靶板,具體數據如下。
1)FSP形破片:直徑為14.8 mm;體長為20.449 mm;材料為艦用945鋼;質量為26 g。
2)靶板:尺寸為800.00 mm×800.00 mm×3.92 mm;材料為艦用945鋼。
破片和靶板的材料模型均采用J-C模型,將表1中的數據代入ANSYS/LS-DYNA軟件中,單元采用SOLID164單元,接觸方式采用面-面侵蝕接觸方式。分別對FSP形破片以初速度1.067 5 km/s和1.238 8 km/s正侵徹靶板的工況進行模擬,圖1和圖2分別為2種初速度下破片侵徹靶板過程中靶板的毀傷模式圖和破片速度的時歷曲線。

圖1 破片初速度為1.067 5 km/s時靶板的毀傷模式圖和破片速度的時歷曲線
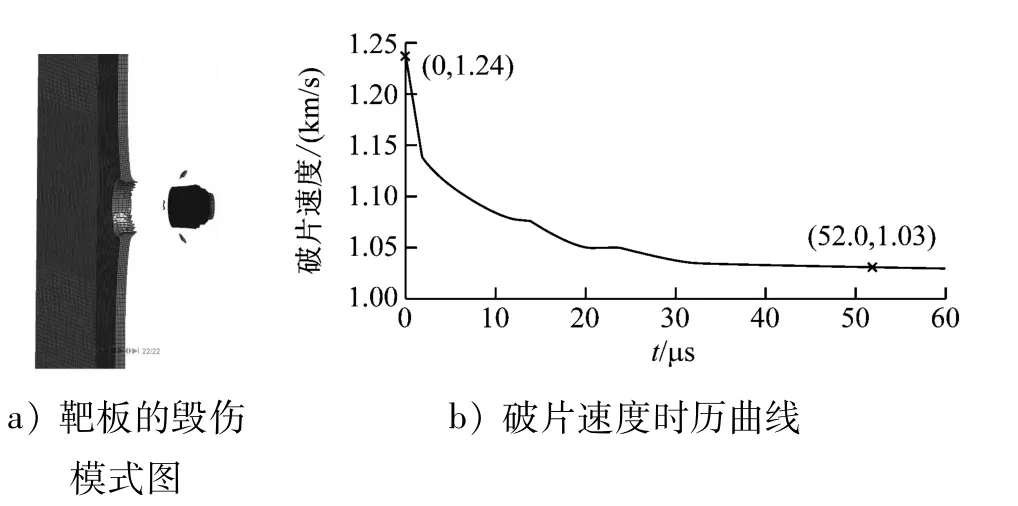
圖2 破片初速度為1.238 8 km/s時靶板的毀傷模式圖和破片速度的時歷曲線
由破片速度時歷曲線可知,FSP形破片以初速度1.067 5 km/s和1.238 8 km/s穿過靶板之后的剩余速度分別為0.866 0 km/s和1.030 0 km/s,破片剩余速度數值仿真結果與文獻[13]中的試驗數據對比見表2。

表2 破片剩余速度數值仿真結果與試驗數據對比
從表2中可看出:數值仿真結果與文獻[13]中的試驗結果相比,偏差小于3%,說明本文采用的模型參數合理,數值仿真方法的準確性較好,可用來對不同形狀破片侵徹鋼靶的性能進行定量分析。
2 靶板抗侵徹性能表征
目前用于評價材料抗侵徹性能的主要參數有彈道極限速度和比吸能,其中比吸能又分為極限比吸能和貫穿比吸能。
2.1 彈道極限速度
彈道極限速度是指穿透靶板的臨界速度,試驗中因存在誤差和不確定性,一般會進行多組穿靶試驗,根據穿靶的概率和破片的速度建立極限速度測試方法。彈道極限速度與彈靶的基本參數(破片形狀、質量、材料、密度和厚度等)密切相關,既能作為裝甲防護的表征評價指標,又可作為特殊條件下對比防護材料的侵徹能力的參考量。
2.2 比吸能
比吸能是指靶板在侵徹過程中吸收的總能量與自身面密度的比值,反映相同質量下抗侵徹能力的強弱。比吸能可根據比式不同分為極限比吸能和貫穿比吸能,其中:極限比吸能是在速度為彈道極限速度v50的情況下靶板的吸能與面密度之比;貫穿比吸能是靶板在被破片貫穿過程中的吸能與面密度之比。
極限比吸能是在v50的基礎上的深化表征量,v50能很好地反映不同靶板之間的抗侵徹能力,但會受靶板厚度和質量等因素的影響,而極限比吸能可很好地避免此類問題。但是,在固定板厚(面密度)情況下,極限比吸能與v50可等效。
根據貫穿比吸能的定義,破片在侵徹穿靶過程中損耗的動能應等于靶板的形變破壞能,因此在應用貫穿比吸能時需滿足條件:破片在侵徹穿靶過程中無質量損耗,且保持剛性;忽略球膨脹效應和摩擦效應。這意味著要想通過貫穿比吸能表征靶板的抗侵徹能力,必須使破片的剛度遠大于靶板的剛度。
綜合來看,在彈道極限速度、極限比吸能和貫穿比吸能等3個表征量中:貫穿比吸能的要求較多,且需規避速度效應帶來的吸能影響;極限比吸能是在彈道極限速度的基礎上的深化表征量,相比極限速度能很好地避免厚度和質量問題帶來的影響。在固定板厚(面密度)的情況下,極限比吸能與彈道極限速度可等效。因此,在此次數值仿真中將彈道極限速度作為表征靶板抗侵徹性能的參量。
3 不同形狀破片穿甲性能有限元分析
3.1 有限元模型的建立
采用ANSYS/LS-DYNA對3種不同形狀的破片侵徹靶板的過程進行模擬,破片和靶板均采用lagrange網格。為更好地對比不同形狀破片的侵徹性能,使3種形狀破片的質量保持一致,均為3.98 g。立方體形破片的邊長為8 mm;圓柱體形破片的長徑比為1.5,直徑為7.574 mm;球形破片的直徑為9.926 mm。靶板的尺寸為240 mm×240 mm×8 mm。破片和靶板均采用SOLID164單元,接觸設置選擇侵蝕接觸,模擬破片在侵徹過程中的消蝕現象。當單元變形引起的損傷超過模型設定的損傷值時,認為此時單元已破壞,不再承載,避免了網格畸變導致計算不收斂的問題。破片的網格尺寸根據形狀的不同劃分為0.2~0.4 mm;靶板采取漸變式網格劃分,中間侵徹區域網格細密,網格尺寸從中間向外側逐漸變大。圖3為破片和靶板網格劃分模型。
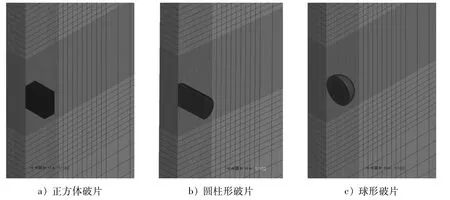
圖3 破片和靶板網格劃分模型
3.2 彈道極限速度計算方法
本文采用數值“逼近法”計算彈道極限速度,具體實現方式[14]如下。
1)建立破片和靶板有限元模型之后,賦予破片初速度進行侵徹過程仿真。
2)若靶板未出現穿靶現象,則適當增加下一發破片的速度;若靶板被穿透,則根據能量曲線得到靶板被穿透后的剩余能量。用初始能量減去剩余能量得到能量差,根據該能量差得到下一發破片的初速度。
3)進行數次仿真計算,直至穿透和未穿透2種情況下破片的初速度在允許范圍內,取2發破片速度的平均值作為彈道極限速度。
圖4為球形破片侵徹過程。

圖4 球形破片侵徹過程

3.3 計算結果及分析
采用數值“逼近法”,針對8 mm厚的艦用945鋼靶,分別求得立方體形、圓柱形(長徑比為1.5)和球形破片的彈道極限速度,結果見表3。

表3 不同形狀破片的彈道極限速度
數值仿真結果表明:3種形狀破片的彈道極限速度由大到小排序為立方體形破片>球形破片>圓柱形破片,即圓柱形破片的侵徹性能最好,球形破片和立方體形破片次之;若以球形破片的侵徹性能為基準,則圓柱形破片(長徑比為1.5)的侵徹性能提升了10.8%,立方體形破片的侵徹性能下降了11.9%。
3種形狀破片在侵徹靶板之后的變形情況見圖5。從圖5中可看出:3種形狀破片侵徹靶板之后的變形情況明顯不同,由于在數值仿真中將破片視為變形體,因此破片在侵徹過程中發生一定的侵蝕,圓柱形破片的侵蝕比例明顯小于球形破片和立方體形破片;圓柱形破片在侵徹過程中與靶板的接觸面積最小,侵徹能量更集中,單位面積上的能量密度最大,因此其侵徹性能最好。

圖5 3種形狀破片在侵徹靶板之后的變形情況
3.4 穿靶機理分析
采用后處理軟件LS-PREPOST對3種形狀破片的侵徹過程作進一步的分析,根據不同時刻的應力云圖和穿靶過程圖像分析其破壞機理。圖6為立方體形破片穿靶過程中靶板的應力云圖。從圖6中可看出:破片在接觸靶板時其應力波就開始在靶板內由接觸點向四周傳播,破片的最大應力在破片頭部位置,靶板的最大應力在靶板與破片接觸的區域;隨著破片繼續侵徹靶板,破片的侵蝕情況越來越嚴重,在9 μs左右時破片已被侵蝕過半;隨著破片逐漸被侵蝕,靶板上的彈坑逐漸縮小,整體被貫穿的區域呈圓臺狀。
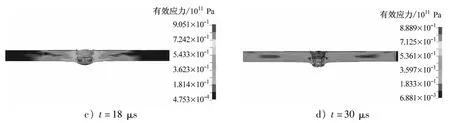
圖6 立方體形破片穿靶過程中靶板的應力云圖

圖7為圓柱形破片穿靶過程中靶板的應力云圖。從圖7中可看出:圓柱形破片因彈身為細長型,其破片的侵蝕情況要明顯好于立方體形破片;在9 μs左右時,破片被侵蝕不超過1/2;立方體形破片在侵徹靶板過程中所受應力要大于圓柱形破片,這是其在侵徹過程中更易發生變形和被侵蝕的原因。下面分析球形破片的侵徹過程。圖8為球形破片穿靶過程中靶板的應力云圖。
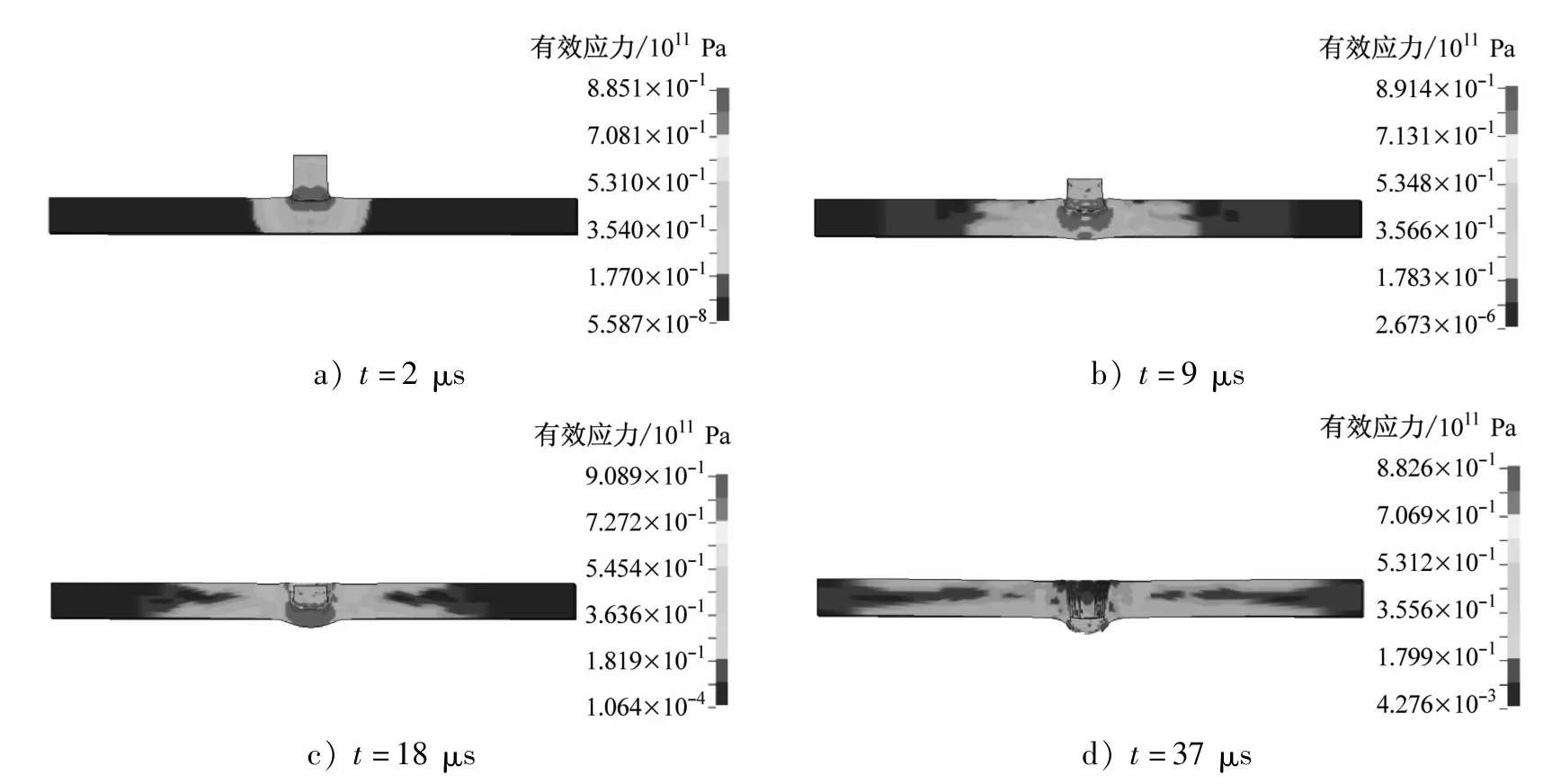
圖7 圓柱形破片穿靶過程中靶板的應力云圖

圖8 球形破片穿靶過程中靶板的應力云圖
通過對比圖6~圖8可知,在3種形狀破片穿靶過程中,球形破片穿靶所用時間最短,其侵蝕情況雖然比圓柱形破片嚴重一些,但最終仍剩余較大體積,同樣具備穿靶之后造成二次傷害的威力。總體來說,3種形狀破片的侵徹過程較為相似,但在穿靶所用時間和破片侵蝕狀況等方面存在一定的差異。
3.5 穿靶耗能分析
為進一步探究不同形狀破片的侵徹性能,計算得到3種形狀破片在不同初始速度下的穿靶動能消耗Ec,計算公式為
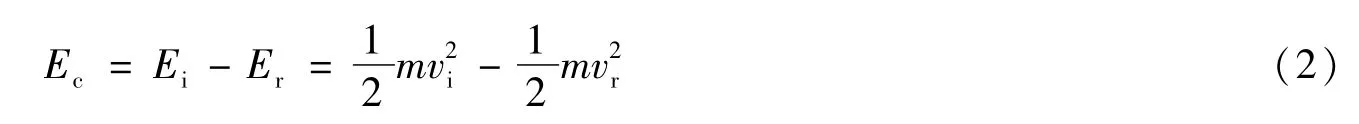
式(2)中:Ei為破片初始動能;Er為破片剩余動能;m為破片質量;vi為破片初始速度;vr為破片剩余速度。根據式(2)求得3種形狀破片在不同初始速度下的穿靶動能消耗Ec見表4。

表4 3種形狀破片在不同初始速度下的穿靶動能消耗Ec
圖9為3種形狀破片在不同初始速度下的穿靶耗能Ec的變化曲線。由表4和圖9可知:破片的侵徹性能越好,其消耗的穿靶動能越少,且穿靶耗能受破片初始速度的影響較小;立方體形破片的侵徹性能最差,侵徹過程中消耗了大量能量,且因在侵徹過程中變形較大,穿靶耗能受破片初始速度的影響較大。

圖9 3種形狀破片在不同初始速度下的穿靶耗能Ec的變化曲線
4 結 語
通過對不同形狀破片侵徹靶板進行數值仿真計算分析,可得到以下結論:
1)3種形狀破片的彈道極限速度由大到小排序為立方體形破片>球形破片>圓柱形破片,即圓柱形破片的侵徹性能最好,球形破片和立方體形破片次之;
2)對于不可視為剛性體的破片來說,圓柱形破片的侵蝕比例要明顯小于球形破片和立方體形破片,與靶板的接觸面積最小,侵徹能量更集中,因此其侵徹性能最好;
3)3種形狀破片的侵徹過程相似,但在穿靶時間和侵蝕狀況等方面存在一定的差異,其中,球形破片的穿靶時間最短,圓柱形破片的剩余體積最多,其二次傷害威力最大;
4)破片的侵徹性能越好,其消耗的穿靶動能越少,且穿靶耗能受破片初始速度的影響較小。

