帶有短暫免疫的分數階SIRS模型的局部穩定性

于智慧，王錚

帶有短暫免疫的分數階SIRS模型的局部穩定性

于智慧1，王錚2

（營口理工學院1. 基礎教研部，2.化學與環境工程學院，遼寧 營口 115014）

研究了帶有短暫免疫的分數階SIRS模型，在模型中，當個體一旦被感染，在一段時間后會轉向為易感個體．討論了該模型解的正則有界性及解的唯一性，給出了在零染病平衡點及有染病平衡點處系統局部漸進穩定的充分條件．

SIRS模型；隨機平均法；平衡點；穩定

近些年來，SIR，SEI，SEIR和SIRS流行病模型的動力學已經獲得了廣泛的關注[1-10]．文獻[11]提供了２個時延的不同的SEIRS模型，并且研究了平衡點的穩定性．文獻[12]提出了喪失疫苗免疫的時延SIRS流行病模型，給出了整數階的帶有短暫免疫的SIRS模型的全局穩定性分析．文獻[13]給出了整數階的帶有短暫免疫的SIRS模型的全局穩定性分析．文獻[14]得到了疾病的非線性發病率和短暫免疫的模型，對該模型進行了定量的分析.

本文將文獻[13]的模型進行推廣，給出了帶有疾病的短暫免疫和線性發病率的分數階模型．相比于整數階模型，分數階模型更具有動態記憶和遺傳性，應用得更廣泛．

1 模型公式和正解

考慮帶有短暫免疫的分數階SIRS時延模型

初始條件為

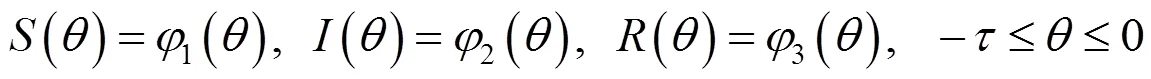
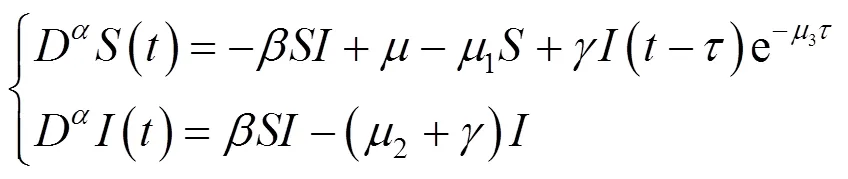
2　零染病平衡點及其穩定性

系統（3）的平衡點滿足系統

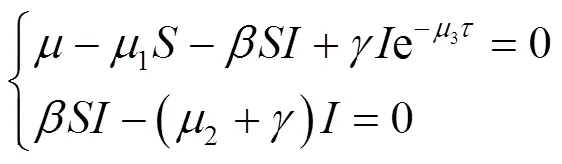
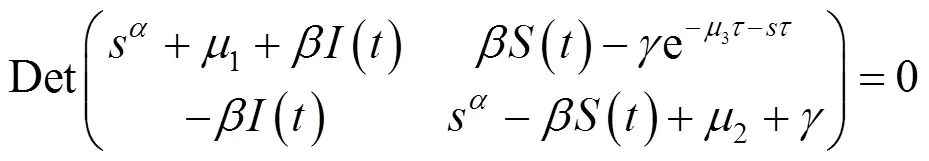
定義再生感染數為

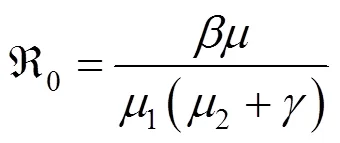
3 有染病平衡點及其穩定性

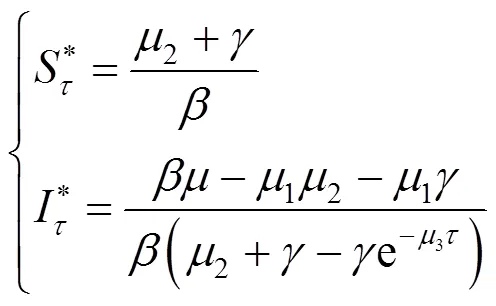
此時沒有零染病平衡點．

在條件（8）下，對應特征方程（5）有方程

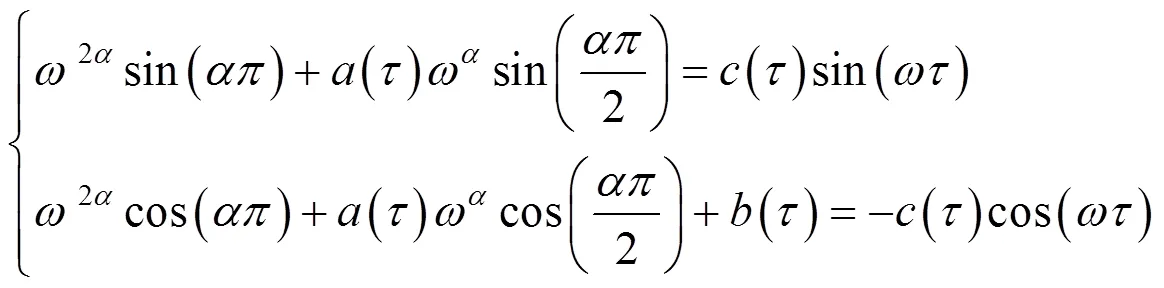
對式（11）平方再加和，可以得到

令

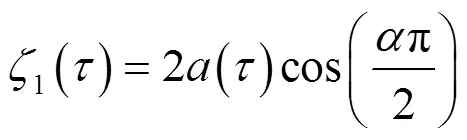
4 結語

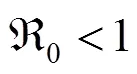
[1] Aron J L．Acquired immunity dependent upon exposure in an SIRS epidemic model[J]．Math Biosci，1988（88）：37-47．

[2] Beretta E，Kuang Y．Modeling and analysis of a marine bacteriophage infection with latency period[J]． Nonlinear Anal Real World Appl，2001（2）：35-74．

[3] Beretta E，Takeuchi Y．Convergence results in SIR epidemic models with varying population sizes[J]．Nonlinear Anal Theory Method Appl，1997，28（12）：1909-1921．

[4] Brauer F，van den Driessche P．Models for transmission of disease with immigration of infectives[J]．Math Biosci，2001，171（2）：143-154．

[5] Busenberg S，Cooke K L．Periodic solutions of s periodic nonlinear delay differential equation[J]．SIAM J Appl Math，1978（35）：704-725．

[6] Li G，Zhen J．Global stability of an SEI epidemic model with general contact rate[J]．Chaos，Solitons and Fractals：Applications in Science and Engineering：An Interdisciplinary Journal of Nonlinear Science，2005，23（3）：997-1004．

[7] Thieme H R，van den Driessche P．Global stability in cyclic epidemic models with disease fatalities[J]．Fields Inst Commun，1999（21）：459-472．

[8] Zeng G，Chen L，Sun L．Complexity of an SIR epidemic dynamics model with impulsive vaccination control[J]．Chaos，Solitions and Fractals：Applications in Science and Engineering：An Interdisciplinary Journal of Nonlinear Science，2005，26（2）：495-505．

[9] Li G，Zhen J．Global stability of a SEIR epidemic model with infectious force in latent，Infected and immune period[J]．Chaos，Solitons and Fractals：Applications in Science and Engineering：An Interdisciplinary Journal of Nonlinear Science，2005，25（5）：1177-1184．

[10] Greenhalgh D，Khan Q J A，Lewis F I．Recurrent epidemic cycles in an infectious disease model with a time delay in loss of vaccine immunity[J]．Nonlinear Anal，2005，63（5-7）：779-788．

[11] Cooke K L，van den Driessche P．Analysis of an SEIRS epidemic model with two delays[J]．J Math Biol，1993（35）：240-260．

[12] Wang K，Wang W，Liu X．Viral infection model with periodic lytic immune response[J]．Chaos，Solitons and Fractals：Applications in Science and Engineering：An Interdisciplinary Journal of Nonlinear Science，2006，28（1）：90-99．

[13] Wen Luosheng，Yang Xiaofan．Global stability of a delayed SIRS model with temporary immunity[J]．Chaos，Solitons and Fractals：Applications in Science and Engineering：An Interdisciplinary Journal of Nonlinear Science，2008，38（1）：221-226．

[14] Kyrychko Y N，Nlyuss K B．Global properties of a delayed SIR model with temporary immunity and nonlinear incidence rate[J]．Nonlinear Anal Real World Appl，2005（6）：495-507．

[15] Kuang Y．Delay differential equations with applications in population dynamics[J]．Academic Press，San Diego，1993，35（5）：452-453

[16] Hale J K，Waltman P．Persistence in infinite-dimensional systems[J]．SIAM J Math Anal，1976，20（2）：335-356．

[17] Hale J K．Theory of functional differential equations[M]．New York：Springer，1978：610-612．

Local stability of a fractional-order SIRS model with temporary immunity

YU Zhihui1，WANG Zheng2

（1. Basic Courses Teaching and Research Department，2. School of Chemical and Environmental Engineering，Yingkou Institute of Technology，Yingkou 115014，China）

The fractional-order SIRS model with temporary immunity is studied．In the model，once an individual is infected，the individual will turn to susceptible individuals after a period of time．The regular boundedness and uniqueness of the solution of the model are discussed．Sufficient conditions for the local asymptotic stability of the system at the zero infection equilibrium point and the infection equilibrium point are given．

SIRS model；stochastic averaging method；equilibrium；stability

1007-9831（2022）11-0022-04

O175

A

10.3969/j.issn.1007-9831.2022.11.004

2022-04-01

校級科研項目（QNL202104）

于智慧（1991-），女，遼寧朝陽人，助教，碩士，從事應用數學研究．E-mail：yuzhihuijiayou@163.com