基于雙層博弈的多臂在軌服務航天器路徑規劃*

高添 吳云華 張梟 岳程斐

1(哈爾濱工業大學(深圳) 空間科學與應用技術研究院 深圳 518055)

2(南京航空航天大學航天學院 南京 211106)

0 引言

隨著航天器在軌服務技術的飛速發展，空間機械臂和裝配有空間機械臂的航天器已成為空間在軌操作的主要對象，將承擔在軌裝配、維修、燃油加注、運輸和空間碎片清理等諸多工作[1,2]。在軌操控作業中，機械臂的運動規劃和控制始終是研究的熱點，例如在笛卡爾空間進行空間機械臂點對點的規劃[3,4]等。隨著在軌操控任務復雜性的提升，如在軌靈巧操作、移動爬行等，未來操控任務均要求空間機械臂能多臂協同地開展工作，例如蜘蛛制造（SpiderFab）[5]等。這類任務除了要求航天器各機械臂實現精確的位置控制外，還要保證各臂自身和相互之間不發生碰撞。因此，考慮自避障的多臂路徑規劃是實現精準在軌操控的前提和基礎。

目前，針對機械臂路徑規劃及避障問題的研究有多種方法。Warren等[6,7]提出利用人工勢場法（Artificial Potential Field，APF）實現機械臂避障，該方法能快速有效地提供安全避障路徑，但是易陷入局部最小點處。Riky等[8]改進人工勢場算法，通過建立輔助函數求解局部極小值問題。Bohlin等[9]提出概率路線規劃（Probabilistic Roadmap Planners，PRMs）方法，通過最小化規劃期間執行的碰撞檢查次數，達到最小化規劃運行時間的目的。Jia等[10]提出一種利用A-star 算法在機械臂的自由運動空間進行路徑搜索，從而實現機械臂無碰撞路徑規劃的方法。Duchoň等[11]對A-star 算法在計算時間和路徑優化方面進行一些改進。Yao等[12]也對傳統A-star 算法進行評價函數加權處理的改進，同時引入人工搜索標記，可以有效快速擺脫障礙陷阱。上述方法多適用于單機械臂路徑規劃及避障等情形，針對多機械臂的研究較少。

與傳統單機械臂僅考慮路徑規劃及過程中實現外部避障的目標有所不同，多機械臂還需要考慮各條臂之間的協同規劃以及自身避障，特別是動態環境下的規劃與自避障。針對多機械臂的路徑規劃問題，可考慮將各臂看成智能體，通過博弈算法等智能策略進行設計。Guo等[13]利用博弈原理改進Q-Learning 算法進行智能體的避障協作路徑規劃。Shen等[14]提出一種博弈論數據融合輔助算法用于無人機在對抗環境中的協作和智能路徑規劃。Lee等[15]將混合博弈策略用于多目標進化算法，應用于無人機系統任務路徑規劃。目前，關于博弈論應用于機械臂路徑規劃的算法還較少。Wang等[16]提出一種基于博弈的快速拓展隨機樹（Rapidly-exploring Random Tree，RRT）算法，將博弈論用于尋找隨機樹的新網格。該方法僅考慮單機械臂路徑規劃，不適用于多機械臂自避障約束下的路徑協同規劃。

為解決多臂航天器的智能規劃問題，本文從多機械臂協同圍捕任務出發，同時考慮圍捕過程中各機械臂的避障問題，提出一種基于雙層博弈的多機械臂路徑規劃方法。本文給定了多臂航天器的基本構型及建立的多機械臂運動學模型；在博弈原理的基礎上建立了多機械臂的博弈模型，通過機械臂末端追蹤目標的博弈實現對目標的圍捕，同時在圍捕過程中嵌套肘關節博弈實現避障，通過雙層博弈實現多條機械臂之間的協同規劃；給出了雙層博弈的基本算法流程及其納什均衡解的求解策略；對多機械臂圍捕案例進行仿真分析，驗證了所提出算法在末端精確跟蹤和肘部避障方面的有效性和實用性。

1 模型及數學原理

1.1 機械臂模型

研究的多臂航天器由一個基座和四條相同的仿人型7-DOF 機械臂組成，機械臂均勻分布在基座四周，其中第1，2，3 關節構成肩關節，第4 關節為肘關節，第5，6，7 關節構成腕關節。利用標準D-H（Denavit-Hartenberg）參數化方法建立機械臂模型，多臂航天器整體構型以及各臂DH 坐標系如圖1 所示。單臂連桿參數列于表1。

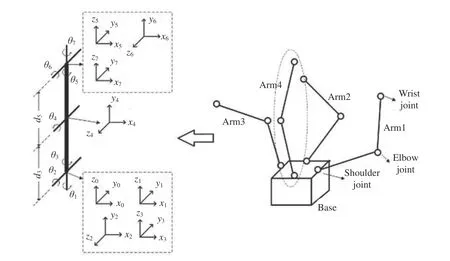
圖1 多臂航天器整體構型及坐標系定義Fig.1 Configuration of the multi-arm spacecraft and the definition of the coordinates

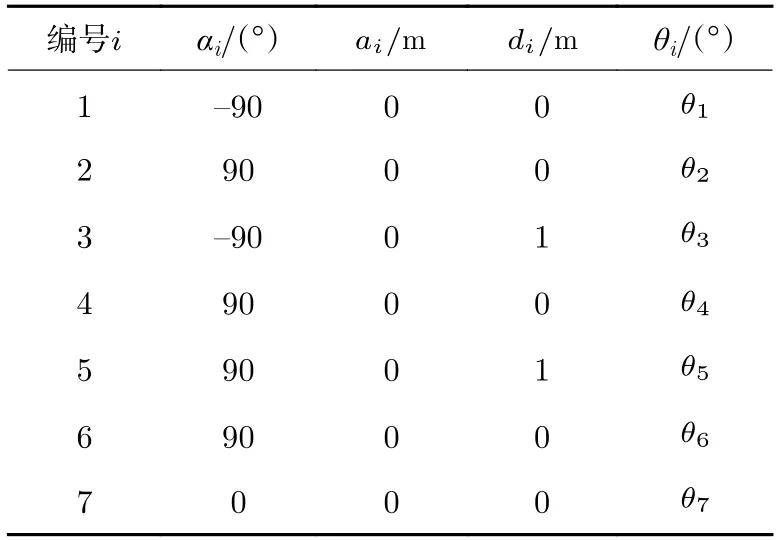
表1 機械臂DH 參數Table 1 DH parameters of the manipulator

針對該仿人型7-DOF 機械臂，定義其基座點B與肩關節點S之間的連線和末端腕關節點W形成的平面為參考平面，其肩關節點S，肘關節點E和腕關節點W形成的平面為臂平面，定義臂平面和參考平面之間的夾角為臂型角φ[17]，機械臂臂型角示意如圖2 所示。由此得知，在給定末端位姿的情況下，仿人型機械臂的臂平面可以繞SW運動，臂型角的相關應用將在1.3 節闡述。

圖2 機械臂臂型角Fig.2 Arm angle of manipulator

1.2 博弈原理

博弈論是研究多個具備進行決策的行為主體在相互作用時，如何選擇合適的決策以達到總體收益最大的方法，也即達到一種均衡狀態，稱之為納什均衡。其中，具備決策行為的主體為博弈方，主體所選擇的決策形成的組合稱之為策略集。根據已制定的收益數學模型，對策略集里的任一組合均能求得一組收益值，其組成的集合稱之為收益集。通過對收益集求納什均衡解得到的一組策略組合即為本次博弈中各博弈方所采取的最佳決策。

綜上所述，博弈過程可以描述如下。

（1）假設共有n個博弈方參與博弈，記為p1，p2，...，pn，每個博弈方可供選擇的策略集分別為S1，S2，...，Sn，每個策略集內的可選擇策略數量分別為n1，n2，...，nn。

（2）假設各博弈方在本次博弈中所采取策略為s1∈S1，s2∈S，...，sn∈Sn。

（3）根據制定的收益數學模型得到博弈方采取的一組策略對應的一組收益(r1，r2，...，rn)=f(s1，s2，...，sn)，所有的收益組合形成收益集R，對收益集R求得納什均衡解，記作

其中，sij表示第i個博弈方選擇對應策略集里的第j個策略。易知，納什均衡解存在唯一解、多解以及無解的情況。

當存在唯一解時，可知此時該唯一解即為本次博弈各方采取的最優策略。

當無解時，此時博弈無法達到均衡，無法保證取得最大收益。為了求得一組策略使得總體收益不至于最差，因此采用max-min 原則進行選取，對于任意s1∈S1，...，si-1∈Si-1，si+1∈Si+1，...，sn∈Sn，滿足

1.3 多機械臂雙層博弈模型

在機械臂模型和博弈理論基礎上給出多機械臂航天器的雙層博弈模型。多臂航天器的四條仿人型機械臂分別為四個博弈方。為簡化模型的復雜程度，將機械臂工作空間柵格化，機械臂末端軌跡視為離散點，機械臂末端的運動視為點到點之間的直線運動。易知，從當前一點運動到下一點共有18 個方向可供選擇，如圖3 所示，加上停止運動共19 個策略，即構成了各條機械臂追捕博弈的策略集。

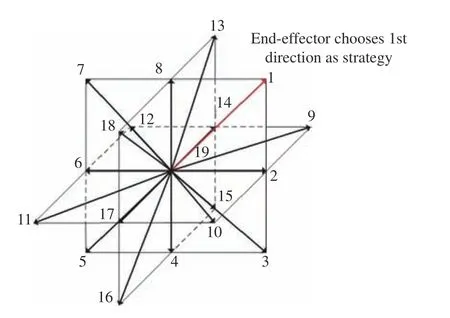
圖3 由19 個可能動作構成的機械臂追捕博弈策略集Fig.3 Strategy set of the manipulator tracking game formed by the 19 potential actions

為評估各機械臂所選擇策略的優劣，引入收益數學模型，構建策略集對應的收益集。收益函數可表示如下：

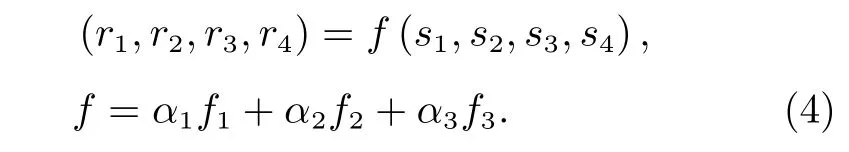
其中，f1為評價各機械臂末端與目標距離的收益函數，f2為評價各機械臂末端之間避障的收益函數，f3為評價各機械臂末端圍捕中心與目標距離的收益函數；α1,α2,α3為權重系數。

定義評價各機械臂末端與目標距離收益函數f1如下：

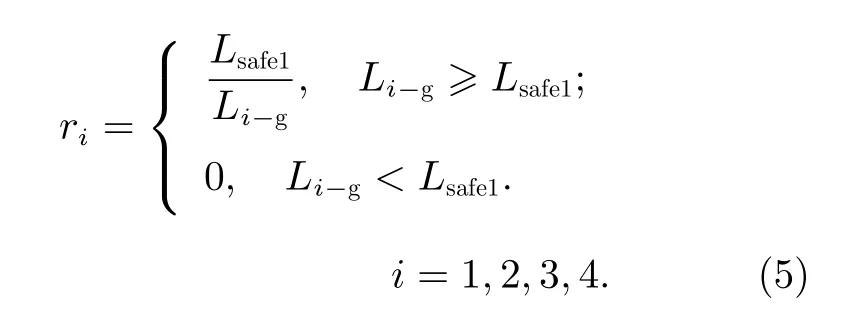
其中，Lsafe1為機械臂末端與目標之間的安全距離，Li-g為第i條機械臂與目標之間的距離。

定義評價各機械臂末端之間避障的收益函數f2如下：

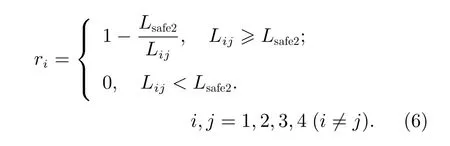
其中，Lsafe2為各機械臂末端之間的安全距離，Lij為第i條 機械臂末端與第j條機械臂末端之間距離的最小值。

定義評價各機械臂末端圍捕中心與目標距離的收益函數f3如下：

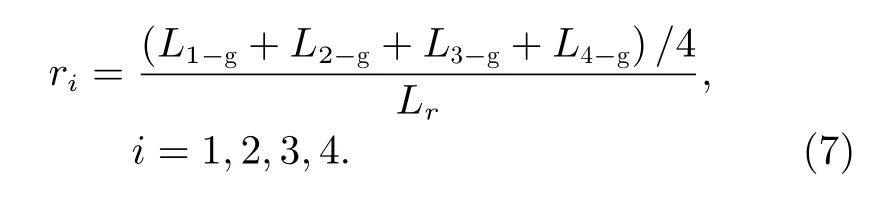
其中，(L1-g+L2-g+L3-g+L4-g)/4 為各機械臂末端形成的四邊形中心與目標的距離，Lr為中心到目標的收益參考距離。

值得注意，安全距離Lsafe1、Lsafe2、參考收益距離Lr及各項分收益占總收益的比例α1，α2，α3均為常數，具體數值由末端離散點之間的步長決定，在此不做深入研究。

在完成多機械臂末端追捕目標博弈后，考慮多機械臂在運動過程中可能發生臂與臂之間的碰撞，增加肘關節之間的避障博弈，考慮在機械臂末端位姿不變的情況下，機械臂的肘關節點E可以繞肩關節點S和腕關節點W之間的連線旋轉，旋轉角度φ即為臂型角，因此，定義機械臂的臂型角為肘關節避障博弈的策略集。同理，構建機械臂肘關節避障博弈的收益集，收益函數表示如下：

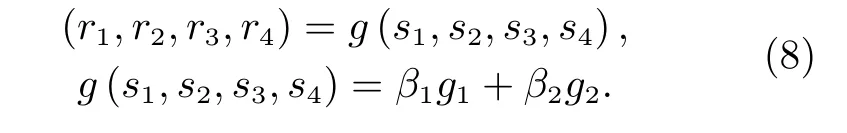
其中，g1為評價各機械臂肘關節之間距離的收益函數，g2為評價各機械臂肘關節之間均勻分布的收益函數。β1和β2為權重系數。

定義評價各機械臂肘關節之間距離的收益函數g1如下：

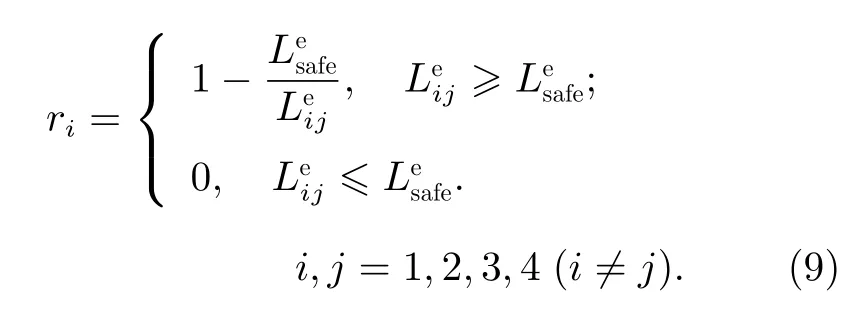
定義評價各機械臂肘關節之間均勻分布的收益函數g2如下：

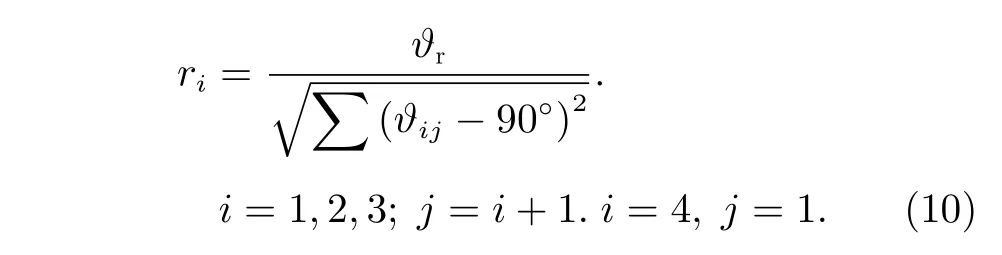
其中，?r為機械臂肘關節均勻分布參考收益角度，θitoj為第i條 機械臂肘關節與第j條機械臂肘關節之間在水平面投影的對心夾角。機械臂肘關節對心夾角如圖4所示。

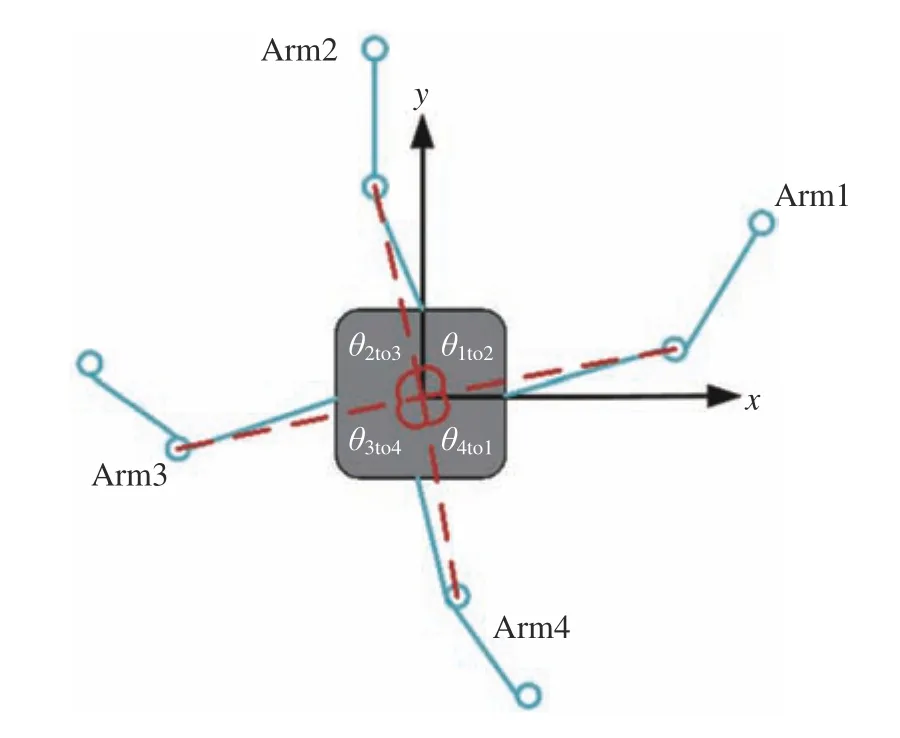
圖4 機械臂肘關節對心夾角Fig.4 Angle against the center of manipulator’s elbow joint

同樣，肘關節避障博弈收益模型中的安全距離，參考收益角度?r和各項分收益所占比例β1，β2均為常數，具體數值由臂型角變化范圍決定。

在機械臂實際運動過程中，考慮機械臂末端運動速度不能突變，以及機械臂臂型角度不能突變，由此引入約束集對策略集加以約束。假定某一機械臂在上一步博弈中末端運動方向為D0，在本次博弈中運動方向為D；在上一步博弈中臂型角為φ0，在本次博弈中臂型角為φ。則由最優化理論，博弈問題可以描述為

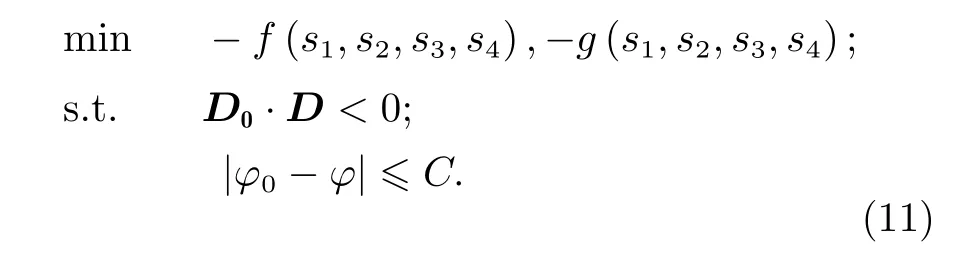
其中，C為臂型角不引起突變的閾值。

同時考慮到機械臂末端為離散點之間的直線運動，為保證末端運動性能，對末端進行梯形速度曲線的直線運動規劃。

2 博弈問題求解

2.1 博弈算法流程

將單步博弈拓展至連續博弈，同時為提高算法的效率，增加肘關節碰撞檢測算法，即各機械臂在進行末端追捕博弈時，檢測當各肘關節之間距離在碰撞安全閾值內時，才執行肘關節避障博弈。由此得到多臂航天器雙層博弈算法流程如下。

（1）設定博弈初始場景，生成柵格模型，初始化各機械臂構型，隨機生成追捕目標位置。

（2）由各機械臂末端與目標之間的相對位置判斷是否捕獲成功（條件為某一機械臂末端與目標距離保持在給定捕獲范圍內）。若捕獲成功，則博弈結束，反之執行（3）。

（3）由各機械臂肘關節相對位置判斷是否需要執行避障博弈（條件為各機械臂肘關節之間距離在碰撞安全閾值內）。若判斷需要，則執行（8），反之執行（4）。

（4）分析各機械臂末端當前約束，得到下一步各機械臂末端可選擇策略，形成末端策略集。

（5）根據式（4）的收益數學模型計算得到末端策略集對應的末端收益集。

（6）對末端收益集求取納什均衡解，得到各機械臂末端下一步最優策略組合。

（7）各機械臂執行該策略組合運動到下一步，并轉到（2）判斷捕獲是否成功。

（8）分析各機械臂末端和肘關節當前約束，得到下一步各機械臂末端和肘關節可選擇策略，形成末端和肘關節策略集。

（9）根據式（4）和式（8）的收益數學模型計算得到末端和肘關節策略集對應的末端和肘關節收益集。

（10）對末端和肘關節收益集分別求取納什均衡解，得到各機械臂末端和肘關節下一步最優策略組合。

（11）各機械臂執行該策略組合運動到下一步，并轉到（2）判斷捕獲是否成功。

如此，完成機械臂追捕目標和肘關節避障雙層博弈策略，機械臂雙層博弈流程如圖5 所示。

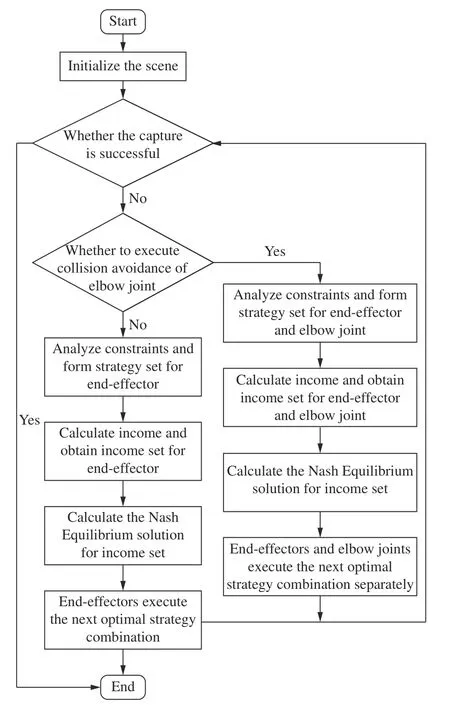
圖5 雙層博弈算法流程Fig.5 Flow chart of the two-level game algorithm

2.2 納什均衡求解算法

在給出納什均衡解滿足的數學表達后，以四方博弈為例，給出求取納什均衡解的完整算法如下。

算法1 納什均衡求解算法

由此，針對多機械臂博弈模型，結合多機械臂雙層博弈算法及多機械臂末端追捕博弈和肘關節博弈的納什均衡解求解策略，即可得到所需的機械臂路徑規劃結果。

3 仿真分析

為驗證上述雙層博弈算法的有效性和實用性，對提出的模型和算法進行仿真分析。以仿人型7-DOF多機械臂為研究對象，設定博弈場景空間范圍為5 m×5 m×5 m，假定多臂航天器能進行精確的姿態位置控制，各機械臂根部的空間位置坐標以及初始構型關節角見表2。

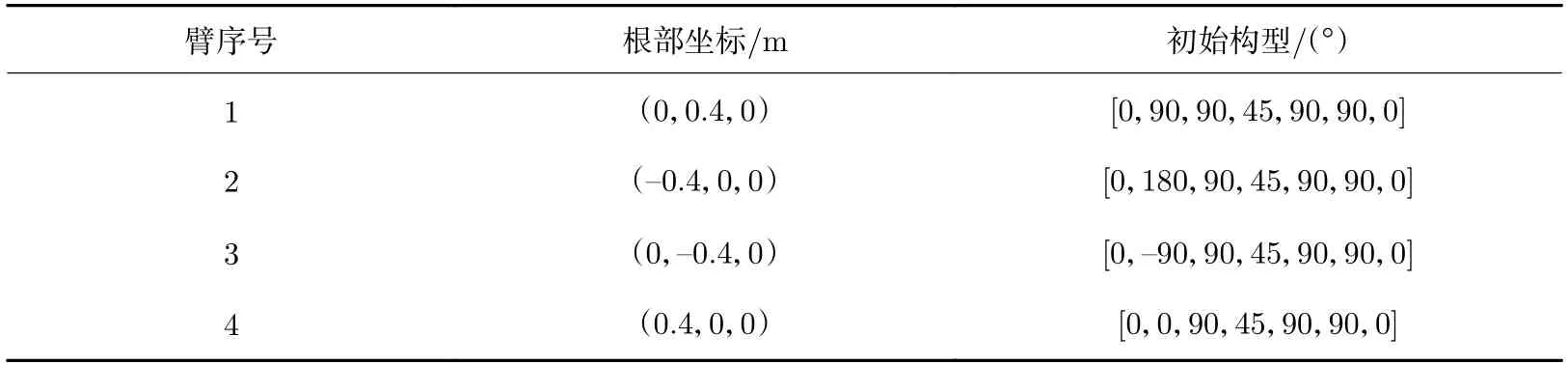
表2 機械臂仿真初始參數Table 2 Initial parameters of the simulation

3.1 機械臂末端追捕博弈仿真

按照多機械臂末端追捕博弈算法對機械臂末端追捕目標的博弈行為進行仿真，得到機械臂末端追捕博弈軌跡如圖6 所示，其中機械臂末端到目標的距離變化如圖7 所示。從圖6 可看出，各機械臂末端對于移動的被追捕目標均能表現出有效的追捕。

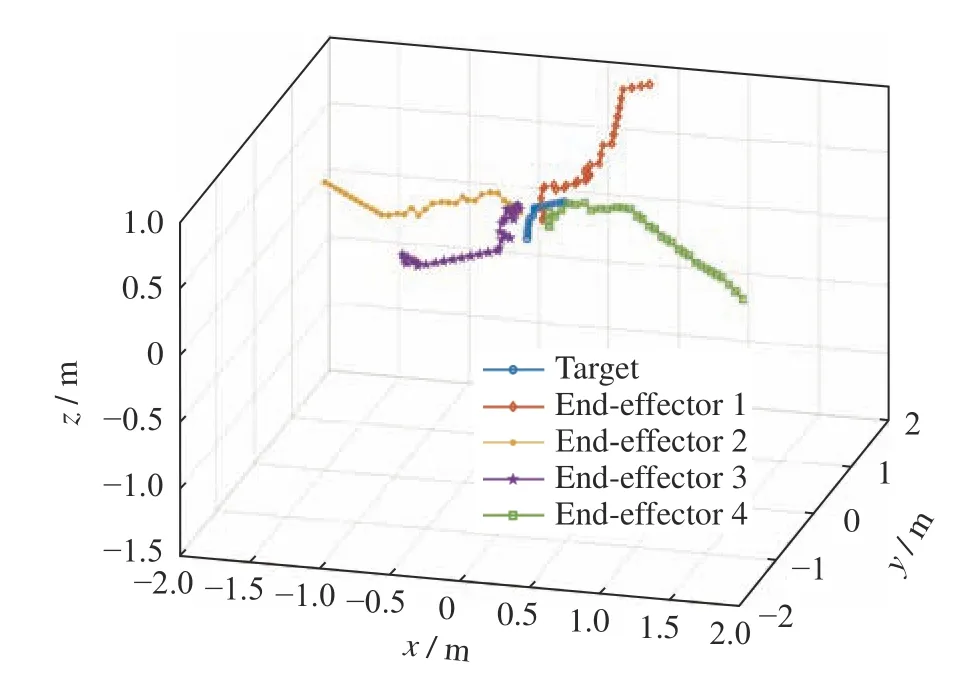
圖6 機械臂末端追捕博弈軌跡Fig.6 Trajectory diagram of the end effector in the hunting game

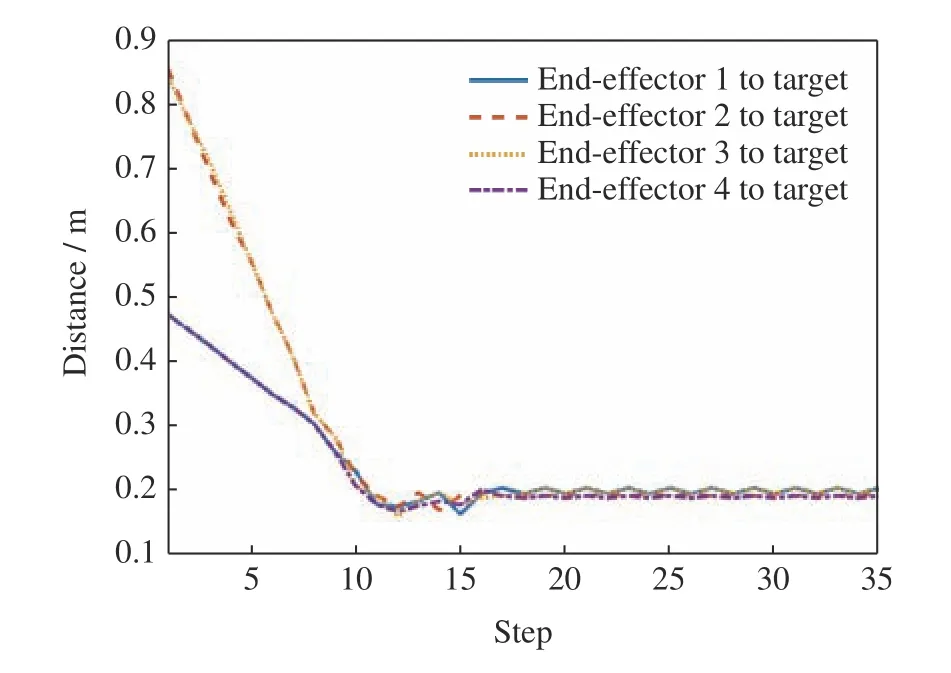
圖7 機械臂末端至目標的距離Fig.7 Distance between multi-manipulator end-effectors and target

3.2 機械臂雙層博弈仿真

按照多機械臂末端追捕和肘關節避障雙層博弈算法進行機械臂雙層博弈全過程仿真實驗，截取的部分機械臂博弈行為如圖8 所示。

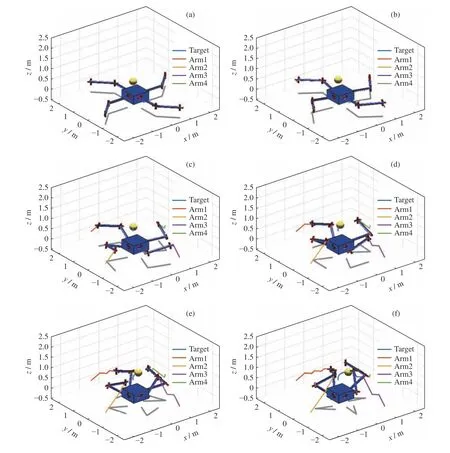
圖8 部分機械臂雙層博弈行為Fig.8 Partial schematic diagram of the manipulators in the two-level game

從圖中可以看出，機械臂在雙層博弈下末端可以快速準確地接近運動目標進行追捕，同時肘關節運動能夠保證避障，臂與臂之間相對于基座的空間分布較為均勻。為了說明均勻性問題，分別提取在有無肘關節避障博弈情況下各機械臂肘關節之間在水平面投影的對心夾角進行對比分析，如圖9 所示。從圖9 可看出，無肘關節避障博弈時，各機械臂肘關節之間對心夾角隨著博弈的進行呈發散狀態；在增加肘關節避障博弈之后，各機械臂肘關節之間對心夾角均能保持在9 0°±10°范圍內，肘關節分布均勻性良好。

圖9 各機械臂肘關節均勻分布指標Fig.9 Index of the distribution of elbow joint

4 結論

針對航天器在軌服務多臂協同操作路徑規劃和避障問題，提出了一種基于雙層博弈理論的多機械臂路徑規劃算法。研究結果表明該算法在實現多機械臂末端追捕目標的同時，可以實現多機械臂肘關節之間的避障功能，且運動過程中各機械臂空間分布呈現均勻的態勢。取得的成果可為多臂航天器智能路徑規劃提供新的思路。