小半徑曲線地段橋上無縫線路伸縮力分析
許晨霄,李怡涵,李一悅,袁 帥,程卓亮
(中國鐵路西安局集團有限公司 西安工務段,陜西 西安 710000)
軌道交通中小半徑曲線出現較多,列車在小半徑曲線橋上運行時,不僅受到梁軌相互作用而產生縱向附加力,還會對軌道結構施加橫向力而產生較大的橫向位移,這使得軌道結構受力更為復雜[1-2]。目前,一些學者對小半徑曲線地段橋上無縫線路的力學特性展開了一定程度的研究[3-5],由于小半徑曲線地段軌道和橋梁結構較為復雜,既有研究中關于小半徑曲線地段梁軌相互作用的力學模型大多為二維平面模型或簡化的三維模型,一定程度上缺乏對無砟軌道、橋梁及墩臺結構力學特性的空間描述,缺乏能滿足精度要求,同時能反映現場實際情況的空間耦合計算模型。針對橋上單元板式軌道無縫線路,以多跨簡支梁橋和大跨度連續梁橋為研究對象,通過建立空間實體精細化有限元計算模型,分別分析了軌溫變化幅度和曲線半徑對無縫線路伸縮工況力學特性的影響。
1 模型的建立
1.1 模型概述
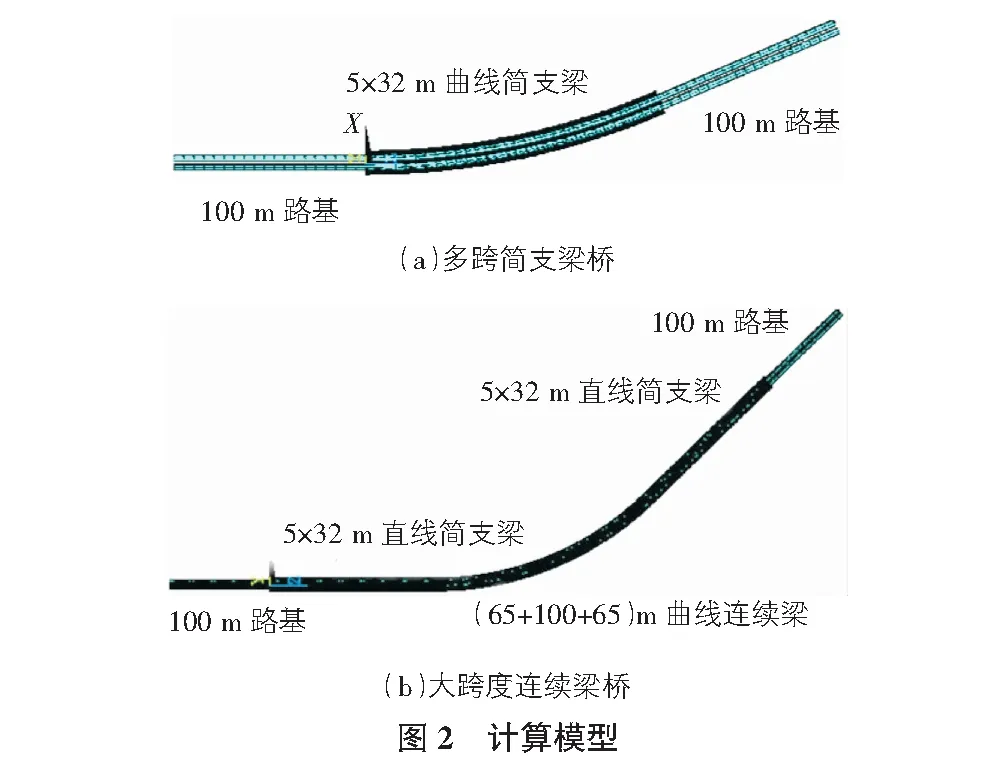
針對多跨簡支梁橋和大跨度連續梁橋,基于梁-板-軌相互作用原理和有限元法,利用有限元軟件ANSYS建立小半徑曲線地段橋上單元板式無砟軌道的空間實體精細化有限元計算模型,多跨簡支梁橋以5跨32 m長的曲線簡支梁橋為例,大跨度連續梁橋以5×32 m直線簡支梁+(65+100+65)m曲線連續梁+5×32 m直線簡支梁橋為例,橋跨結構如圖1所示。

1.2 計算參數
橋上單元板式軌道主要由鋼軌、扣件系統、軌道板、底座板和橋梁梁體等組成,鋼軌采用CHN60;單組扣件的最大縱向阻力為10 kN,記為10 kN/組,彈塑性臨界位移為2 mm;扣件垂向剛度和橫向剛度的大小分別為35 kN/mm和50 kN/mm;橋臺縱向水平剛度取3 000 kN/cm,簡支梁橋墩縱向水平剛度取500 kN/cm,連續梁橋墩縱向水平剛度取4 000 kN/cm,橋臺(墩)的橫向水平剛度的取值同縱向水平剛度的,建立如圖2所示的計算模型。
2 曲線內外側計算結果分析
參考《鐵路無縫線路設計規范》和《鐵路軌道設計規范》,橋梁整體溫度荷載取為年溫差30 ℃,無砟軌道鐵路設計鎖定軌溫,宜按式(1)進行計算:
(1)
其中,Tmax為最高軌溫;Tmin為最低軌溫;ΔTk為設計鎖定軌溫修正值,可取0 ℃~5 ℃。
本文參考某地一線路進行參數取值,最高軌溫為58.7 ℃,最低軌溫0.2 ℃。設計鎖定軌溫鎖定范圍宜為0 ℃~5 ℃,線路實際鎖定軌溫為30 ℃±5 ℃,滿足設計要求,溫升時最大溫差達33.7 ℃,溫降時最大溫差達34.8 ℃。
在小半徑曲線無縫線路計算中,曲線內外兩側鋼軌的力學特性有所不同,因此,首先對雙線線路四根鋼軌的位移與軌道幾何形位進行分析,以便在無縫線路設計時可以偏安全考慮,雙線線路中的四根鋼軌由曲線內側向曲線外側分別記為1號鋼軌、2號鋼軌、3號鋼軌、4號鋼軌。在橋梁溫升30 ℃的情況下,半徑為400 m的曲線地段內外側鋼軌縱向位移如圖3所示。
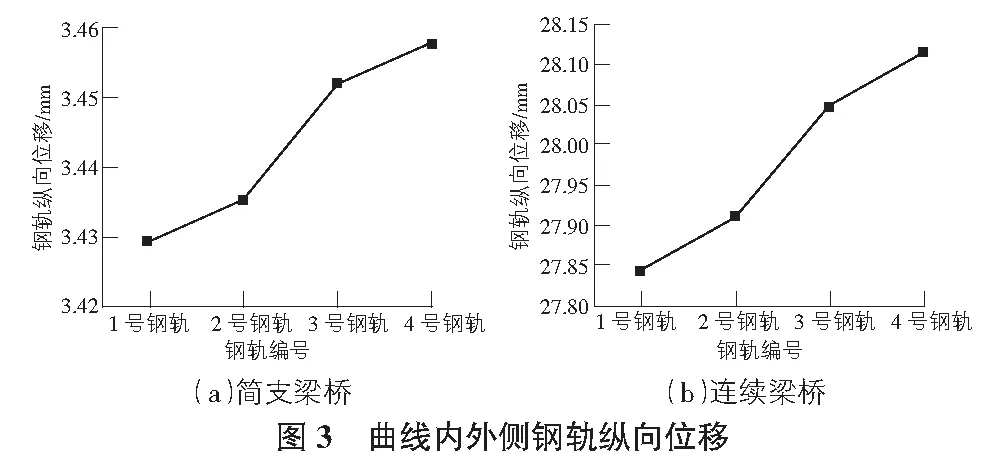
分析圖3可知,曲線外側線路兩根鋼軌的縱向位移極值均大于曲線內側所得計算結果。
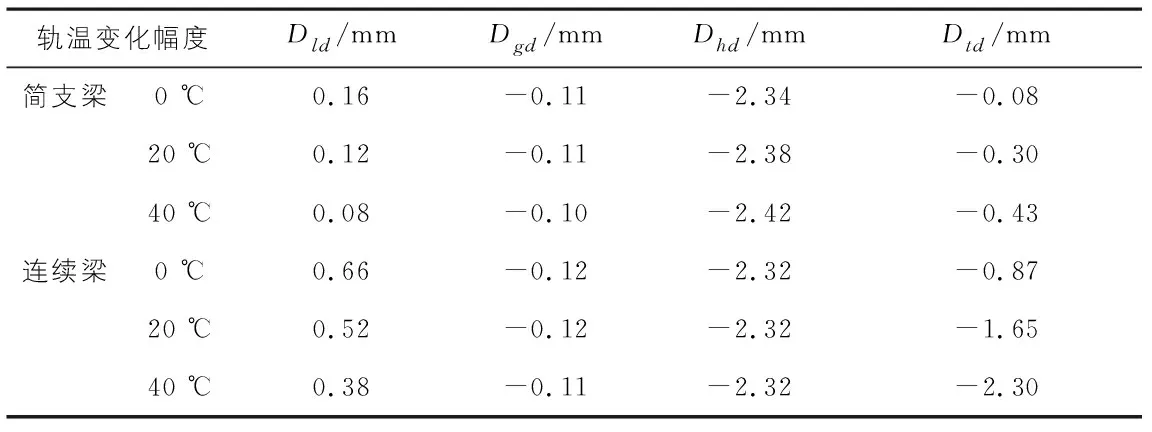
軌道的幾何形位主要包括水平、軌距、高低和軌向。根據《鐵路軌道設計規范》中3.4節的有關規定,本文所采用的軌道靜態不平順限值如表1所示(根據速度等級80 km/h 表1 軌道靜態不平順限值 mm (2) 其中,z為線路里程;L為弦線長度;f(z)為不平順幅值;g(z)為弦測法計算值。 在橋梁溫升30 ℃的情況下,半徑為400 m的曲線地段內外側鋼軌水平偏差和軌向偏差的計算結果分別如圖4,圖5所示,軌道靜態不平順極值如表2所示。表2中,Dld,Dgd,Dhd,Dtd分別為鋼軌最大水平偏差、軌距偏差、高低偏差和軌向偏差。 分析圖4,圖5及表2可知,各項靜態不平順極值均滿足其限值要求;簡支梁橋和連續梁橋上鋼軌軌距偏差和高低偏差相差較小,連續梁橋上鋼軌水平偏差和軌向偏差大于簡支梁橋上的計算結果,連續梁邊跨和跨中出現水平偏差極大值;連續梁曲線內外側水平偏差的差異性較大,軌向偏差在連續梁梁端發生突變而產生極大值,遠大于簡支梁部分所得計算結果,連續梁橋上曲線外側的鋼軌水平偏差大于曲線內側0.44 mm,而曲線外側的軌向偏差小于曲線內側0.14 mm。 表2 曲線內外側線路靜態不平順極值 曲線橋上的無縫線路鋼軌軸向力會對橫向梁軌相互作用產生影響,而軌溫變化也是引起鋼軌軸向力的重要因素之一[6]。為了明確軌溫變化對小半徑曲線橋上梁軌相互作用的影響,在橋梁溫升30 ℃的情況下,分別分析鋼軌升溫0 ℃,20 ℃,40 ℃下無縫線路的力學特性,簡支梁橋和連續梁橋上不同軌溫條件下各結構受力與變形分別如圖6,圖7所示,其最大值見表3~表5。表3~表5中,Fr為鋼軌伸縮力;Fpz,Fpx分別為橋梁墩臺沿線路方向最大受力、垂直線路方向最大受力;Drz,Drx和Dry分別為鋼軌最大縱向位移、橫向位移和垂向位移;ΔDrtz,ΔDrtx分別為軌板最大縱向相對位移、橫向相對位移。 表3 不同軌溫條件下各結構伸縮力及橋梁墩臺受力最大值 表4 不同軌溫條件下軌道結構位移極值 表5 不同軌溫條件下軌道靜態不平順極值 分析圖6,圖7及表3~表5可知,軌溫變化對鋼軌伸縮力、鋼軌縱向位移、鋼軌垂向位移、軌板縱向相對位移、橋梁墩臺沿線路方向受力、鋼軌軌距偏差、鋼軌高低偏差的影響較小,而對鋼軌橫向位移、軌板橫向相對位移、橋梁墩臺垂直線路方向受力、鋼軌水平偏差、鋼軌軌向偏差的影響較大;當軌溫從0 ℃增加到40 ℃時,簡支梁橋上鋼軌橫向位移、軌板橫向相對位移、橋梁墩臺垂直線路方向受力、鋼軌軌向偏差分別增大了5.19 mm,0.15 mm,237.949 kN,0.35 mm,增幅分別為314.5%,107.1%,458.1%,437.5%,437.5%;當軌溫從0 ℃增加到40 ℃時,連續梁橋上鋼軌橫向位移、軌板橫向相對位移、橋梁墩臺垂直線路方向受力、鋼軌軌向偏差分別增大了4.65 mm,0.43 mm,721.626 kN,1.43 mm,增幅分別為132.5%,165.4%,143.8%,164.4%。 綜上所述,軌溫升高對梁軌縱向相互作用的影響較小,會加劇梁軌橫向相互作用,因此,小半徑曲線地段橋上無縫線路伸縮工況計算時必須同時考慮橋梁梁體與鋼軌的溫度作用。 鋼軌溫升時的最大溫差為33.7 ℃,本節分析在橋梁升溫30 ℃與鋼軌升溫33.7 ℃的溫度荷載作用下,不同曲線半徑下無縫線路受力與變形的變化規律,各結構力與位移的最大值如表6~表8所示。 表6 不同曲線半徑下各結構伸縮力及橋梁墩臺受力最大值 表7 不同曲線半徑下軌道結構位移極值 分析表6~表8可知,鋼軌伸縮力、鋼軌縱向位移、橋梁墩臺沿線路方向受力隨曲線半徑的增大而增大,鋼軌橫向位移、鋼軌垂向位移、軌板橫向相對位移、橋梁墩臺垂直線路方向受力隨曲線半徑的增大而減小;簡支梁橋上軌板縱向相對位移整體隨曲線半徑的增大而增大,而在兩側橋臺位置隨曲線半徑的增大而減小,且在橋臺位置出現位移最大值,連續梁橋上軌板縱向相對位移隨曲線半徑的增大而增大;曲線半徑的增大減小了梁軌橫向相互作用,因此使伸縮力與墩臺沿線路方向受力隨曲線半徑的增大而增大,而墩臺垂直線路方向的受力大幅度減小。 表8 不同曲線半徑下軌道靜態不平順極值 曲線半徑對梁軌縱向相互作用的影響較小,當曲線半徑從400 m增大至600 m時,簡支梁橋上鋼軌伸縮力、鋼軌縱向位移、橋梁墩臺沿線路方向受力的最大值分別增大了4.937 kN,0.09 mm,14.852 kN,增幅分別為2.61%,2.69%,2.21%,而當曲線半徑從600 m增至1 200 m時,簡支梁橋上鋼軌伸縮力、鋼軌縱向位移、橋梁墩臺沿線路方向受力的最大值分別增大了1.590 kN,0.06 mm,9.766 kN,增幅分別為0.82%,1.75%,1.42%;當曲線半徑從400 m增大至600 m時,連續梁橋上鋼軌伸縮力、鋼軌縱向位移、橋梁墩臺沿線路方向受力的最大值分別增大了12.657 kN,0.40 mm,2.385 kN,增幅分別為2.44%,1.46%,0.31%,而當曲線半徑從600 m增至1 200 m時,簡支梁橋上鋼軌伸縮力、鋼軌縱向位移、橋梁墩臺沿線路方向受力的最大值分別增大了6.868 kN,0.19 mm,1.405 kN,增幅分別為1.29%,0.68%,0.18%,由此說明了曲線半徑增大至600 m時,鋼軌伸縮力、鋼軌縱向位移、橋梁墩臺沿線路方向受力基本趨于穩定。鋼軌強度的檢算受伸縮力的影響較大,“以直代曲”計算出的小半徑曲線無縫線路伸縮力偏大,曲線伸縮力可以通過直線線型計算,檢算結果偏于安全。 曲線半徑對梁軌橫向相互作用的影響較大,當曲線半徑從400 m增大至1 200 m時,簡支梁橋上鋼軌橫向位移、軌板橫向相對位移、橋梁墩臺垂直線路方向受力的最大值分別減小了3.54 mm,0.10 mm,166.068 kN,降幅分別為58.90%,37.04%,66.03%,連續梁橋上鋼軌橫向位移、軌板橫向相對位移、橋梁墩臺垂直線路方向受力的最大值分別減小了4.58 mm,0.44 mm,734.599 kN,降幅分別為61.73%,69.84%,66.18%。簡支梁橋上橋梁墩臺垂直線路方向受力均小于沿線路方向受力,而連續梁橋上曲線半徑為400 m,500 m時的橋梁墩臺垂直線路方向受力大于沿線路方向受力,曲線半徑為600 m時橋梁墩臺垂直線路方向受力小于沿線路方向受力,兩者相差3.27%,故當曲線半徑小于600 m時,連續梁橋上墩臺垂直線路方向受力基本大于沿線路方向受力。由此可知,當采用“以直代曲”的計算方法計算小半徑曲線地段大跨度連續梁橋上無縫線路時,忽略了梁軌橫向相互作用引起的墩臺垂直線路方向受力,從而可能造成曲線橋墩剛度和強度的不足。 曲線半徑對鋼軌水平偏差、軌距偏差、高低偏差的影響較小,而對軌向偏差的影響較大,軌向偏差隨曲線半徑的增大而減小;當曲線半徑從400 m增大至1 200 m時,簡支梁橋上鋼軌軌向偏差減小了0.23 mm,降幅為58.97%,連續梁橋上軌向偏差減小了1.34 mm,降幅為64.11%。 綜上所述,小半徑曲線地段梁軌縱向相互作用下各結構縱向力與位移隨曲線半徑的增大而增大,而梁軌橫向相互作用下各結構縱向力與位移隨曲線半徑的增大而減小;曲線半徑增大至600 m時,鋼軌伸縮力、鋼軌縱向位移、橋梁墩臺沿線路方向受力基本趨于穩定,“以直代曲”計算出的小半徑曲線無縫線路伸縮力偏大,曲線伸縮力可以通過直線線型計算,檢算結果偏于安全;當曲線半徑小于600 m時,采用“以直代曲”的計算方法計算小半徑曲線地段大跨度連續梁橋上無縫線路時,忽略了梁軌橫向相互作用引起的墩臺垂直線路方向受力,從而可能造成曲線橋墩剛度和強度的不足。 1)軌溫升高會加劇梁軌橫向相互作用,因此,小半徑曲線地段橋上無縫線路伸縮工況計算時必須同時考慮橋梁梁體與鋼軌的溫度作用。2)“以直代曲”計算出的小半徑曲線無縫線路伸縮力偏大,曲線伸縮力可以通過直線線型計算,檢算結果偏于安全。3)當曲線半徑小于600 m時,采用“以直代曲”的計算方法計算小半徑曲線地段大跨度連續梁橋上無縫線路的力學特性時,忽略了梁軌橫向相互作用引起的墩臺垂直線路方向受力,從而可能造成曲線橋墩剛度和強度的不足。


3 軌溫變化幅度的影響




4 曲線半徑的影響



5 結語

