例談數形結合在求解三角形最值問題中的妙用
安徽省巢湖市第四中學 (238000) 車承梅
解三角形中經常會出現求最值或范圍類的問題,此類問題有時難度相對較大,有一定的運算量,但是我們可以試著從幾何圖形的直觀性入手,借助于平面幾何的知識,將代數問題轉化為幾何問題去解決,這樣可以大大減少計算量,從而達到事半功倍的效果.下面將通過幾個實例去探究數形結合在求解三角形的最值(或范圍)問題中的妙用.
例1 △ABC中,內角A,B,C所對的邊分別為a,b,c,且(sinA-sinC)2=sin2B-sinAsinC,b=3,則△ABC的面積的最大值為.
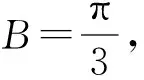
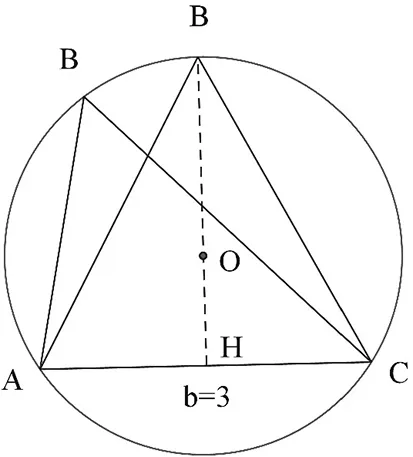
圖1
評注:此題的條件屬于邊角對應型的,于是聯想到圓的性質,即同一條弧所對的圓周角相等,這樣就知道了點B的活動范圍,從而使問題迎刃而解.
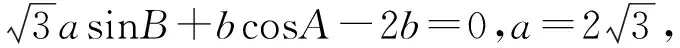
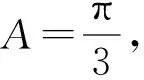
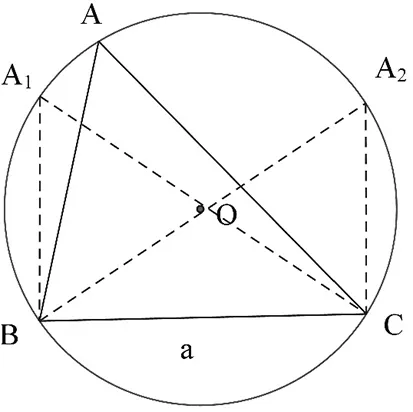
圖2
由條件可知,點A在優弧BC上運動(不與B,C重合),當AB⊥BC時,△ABC為直角三角形(圖中為△A1BC),此時b最大,c最小,且b=4,c=2,所以b-c=2;當AC⊥BC時,△ABC也為直角三角形(圖中為△A2BC),此時b最小,c最大,且b=2,c=4,所以b-c=-2,當點A在點A1與點A2之間時,△ABC為銳角三角形,所以b-c∈(-2,2).
評注:本例與實例1相似,條件都屬于邊角對應型,此類問題都可以借助于三角形的外接圓來解決.
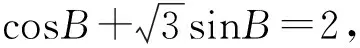
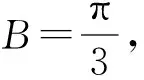
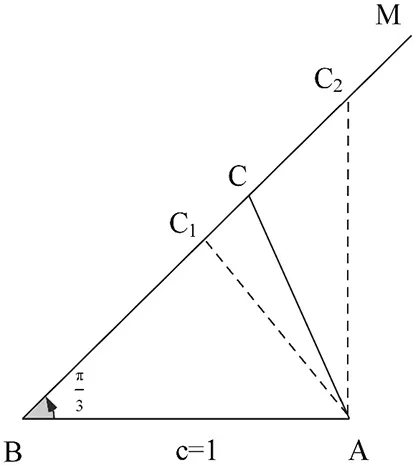
圖3
評注:此題為邊角不對應型,根據條件找到點C的活動范圍,從而觀察出使△ABC為銳角三角形的位置.
例4 在△ABC中,內角A,B,C的對邊分別為a,b,c,已知a+b=8,2sin(A+B)=sinA+sinB,則△ABC面積的取值范圍為.
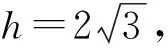
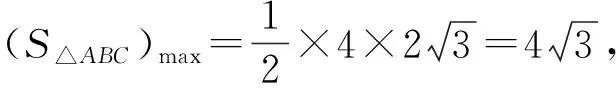
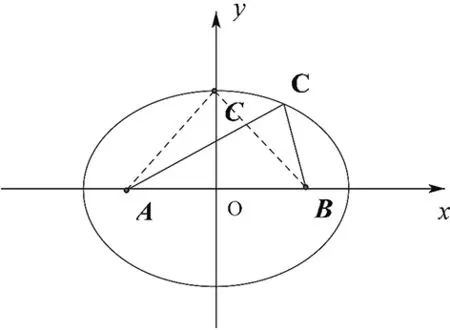
圖4
評注:焦點三角形是橢圓中的一個重要三角形,有很多性質可以利用,而本題通過a+b=8聯想到橢圓的定義,從而利用焦點三角形的性質輕松的解決了問題,可謂“妙極”.
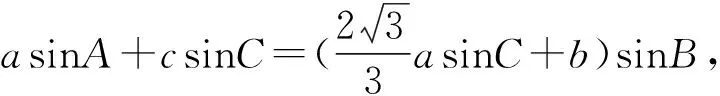
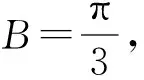
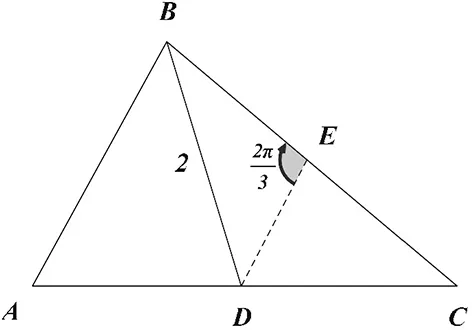
圖5
評注:此題利用中位線的性質,將△ABC的面積轉化為△BDE的面積,使之成為與實例1的相同的情形.其實,本題還可以進行擴展,當點D在線段AC上任意分點位置,都可以作平行線,從而利用相似性轉化為實例1的情形去解決,這也是我們常說的“解一題而通一類”.

