對一道經典試題的再研究

江蘇省連云港市外國語學校 (222003) 陳 洋

《普通高中數學課程標準(2017年版)》要求“提升學生的數學素養，引導學生會用數學的眼光觀察世界，會用數學思維思考世界，會用數學語言表達世界.”“高中數學課程以學生發展為本，落實立德樹人根本任務，培育科學精神和創新意識，提升數學學科素養.”而解題教學又是提升數學學科素養的載體，因此，在平常的教學中，我們要善于發現有價值的數學問題，通過有效的教學手段，讓深度學習發生，進而發展學生的核心素養.

1 習題呈現

題目過點P(2，1)的直線l交x軸，y軸的正半軸于A,B兩點，O為坐標原點.求△AOB面積S取最小值時直線l的方程.

這是筆者在開學初新授蘇教版《選擇性必修一》(2019)直線方程章節時選的一道經典題目，這道題題干簡潔、內涵豐富，解法頗多，直線搭臺，不等式唱戲，是難得一道培養學生思維品質的好題.

2 解法探究

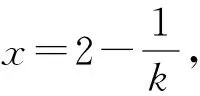
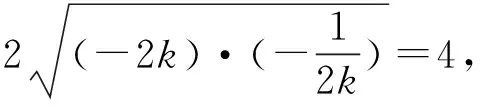
點評：從直線方程的點斜式入手，求出與x軸，y軸交點，代入面積公式，再利用基本不等式，這里要注意“一正，二定，三相等”的條件.

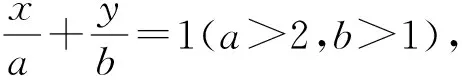
點評：直接從截距入手，利用基本不等式求解，運用基本不等式時，一定要注意成立條件.

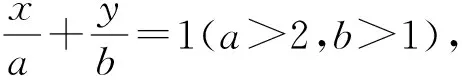
點評：將其中一個變量用另一個變量表示，即消元，它是處理二元變量問題的基本方法，再通過添項，拆項構造基本不等式進行求解.

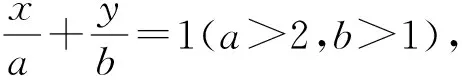
點評：用函數方程思想，轉化成一元二次方程，利用根的判別式求解，注意△≥0只是保證方程有大于2的根的必要條件，要對S=4時，實數a是否大于2進行檢驗.

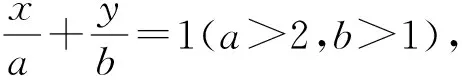
點評：由“1”想到三角代換，注意對參變量角θ的范圍限制，再利用基本不等式求解.

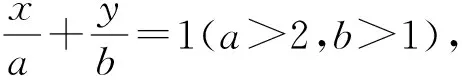
點評：巧妙地構造定比，利用定比分點坐標公式，結合基本不等式求解.

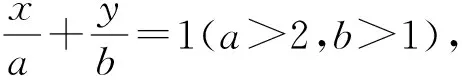
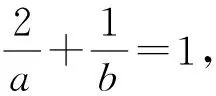
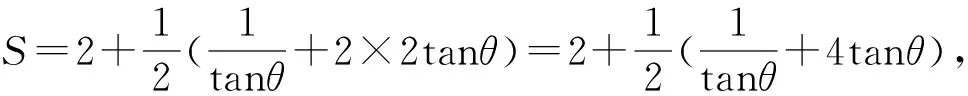
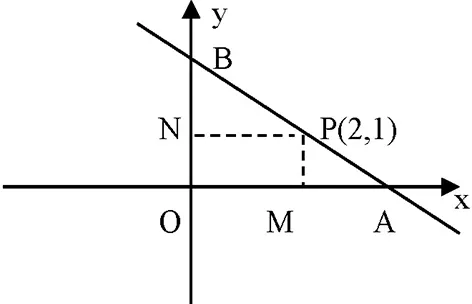
圖1

點評：引入“角參數”，利用解三角形知識，構造基本不等式求解.

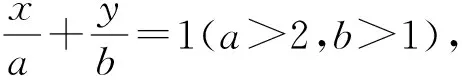
點評：將其中一個變量用另一個變量表示，即消元，它是處理二元變量問題的基本方法，再利用導數求最值.

3 變式探究

變式(1)求過點P(2，1)且在兩正半軸上的截距之和最小的直線方程；

(3)求過點P(2,1)且與兩坐標軸圍成一等腰直角三角形的直線l方程;

(5)過點P(6，4)作直線l交直線y=2x于第一象限內的點A，交x軸正項于點B，求△AOB面積最小值時l的方程；

4 結語

在上述解題中，不同層次的學生都能獲得不同程度的知識構建機會，讓他們感受到數學活動的快

樂和對數學學習的興趣，激發了對數學探究活動的欲望.縱觀上述解法，有必要對其進行比較、評價、篩選，甄別出最優的解法，或提出這些解法中易錯點、注意點，或提煉出問題探索中發現的有價值的數學思想方法，培育學生的數學學科素養.課堂上數學題并不在于多，而在于充分挖掘每一道題的內涵與外延，使每一道題的功能達到最大化，對在課堂中的數學問題，不是簡單地給學生講懂，而要講變化(式)、講拓展、講思辨(方法)，使學生以不變應萬變，只有這樣，才達到“授之以漁”的目的.