基于深度學習LDAMP 網絡的量子狀態估計

林文瑞 叢 爽

在量子力學中,量子狀態密度矩陣包含了量子系統的全部信息,是量子信息處理和量子控制研究的基礎.根據海森堡不確定性原理[1],對量子系統的每一次測量都會破壞其原有的狀態,這使得人們無法通過直接對一個量子系統進行測量來獲得量子系統的狀態,只能測量到量子系統的狀態在某個投影方向上的投影(坍縮)結果,再通過多次測量的統計結果,計算出各投影分量的概率對真實量子狀態進行估計[2].為了解決量子態的估計問題,1957 年Fano[3]提出了量子層析的方法,它是通過對一個量子狀態進行多次投影測量,根據測量值與量子態直接的關系式,聯立方程求解出量子狀態.該方法需要制備量子狀態的大量全同副本,并進行重復地測量來進行量子態估計.隨著量子理論的逐步完善,1969 年Cahill和Glauber[2]提出利用重復測量獲取的量子概率統計數據重構出量子態的密度矩陣來恢復量子狀態信息,奠定了量子態層析的基礎.一個n比特量子系統狀態的密度矩陣ρ∈Cd×d的維數為d×d,并同時具有半正定,單位跡和共軛對稱的性質,其中d=2n.由于待估計的ρ的未知元素數目為d×d=4n個,所以該系統的完備測量次數為 4n,是隨著量子維數呈指數增加[4].為了解決測量次數隨量子位指數增長的問題,人們根據壓縮感知(Compressive sensing,CS)理論[5]將量子態密度矩陣通過高維測量矩陣投影到維數很低的壓縮矩陣上,只要測量矩陣滿足限制等距特性(Restricted isometry property,RIP)[6],就可以利用壓縮后的低維壓縮矩陣通過求解一個優化問題精確重構出待估計的密度矩陣[7-9].

在實際量子測量過程中,測量噪聲的存在是不可避免的,并且可以被假定為高斯噪聲.在量子狀態估計算法研究中,Smith 等[10]基于最小二乘法從含有噪聲的數據中實現了4 比特量子狀態估計.Li等[11]基于壓縮感知將交替方向乘子法(Alternating direction multiplier method,ADMM)運用到量子態估計中[12],給出了算法迭代優化形式,并在5 比特的量子狀態密度矩陣估計中獲得了較高的估計精度.ADMM 算法是一種求解分布式凸優化問題的計算框架,在圖像處理及恢復、統計學習和量子態估計等領域有著廣泛應用.Smolin 等[13]提出了一種從加性高斯噪聲測量中計算最大似然量子態的有效方法,其最壞時間復雜度為O(d4).但是這些優化算法在量子態重建過程中都會需要較多的計算內存和計算時間.對于高維量子系統,重建過程中需要測量和處理的數據會很多,這樣會導致所需的計算資源和計算時間增長很快.Metzler 等[14]提出DAMP 算法,它是一種基于壓縮感知的迭代稀疏信號恢復算法,通過在算法中添加Onsager 校正項[14-15],修正每次迭代時有效噪聲的偏差,改進了基于去噪的迭代閾值(Denoising-based iterative threshold,DIT)算法收斂速度慢的問題.Liu 等[16]采用卷積神經網絡的降噪自動編碼器,從帶有噪聲的密度矩陣中重建出高精度的密度矩陣.

本文基于壓縮感知理論,結合深度學習網絡,提出一種采用深度學習網絡來估計量子狀態密度矩陣的方法.將密度矩陣視為二維自然圖像信號,采用基于學習降噪的近似消息傳遞(Learned denoising-based approximate message passing,LDAMP)神經網絡[17],將去噪卷積神經網絡(Denoising convolutional neural network,DnCNN)的圖像降噪器[18]融合到基于去噪的近似消息傳遞(Denoisingbased approximate message passing,DAMP)算法[19]中.此外,還提供一個關于LDAMP 在量子狀態估計中的漸近收斂性能的分析框架—狀態演化(State evolution,SE)方程[17]來預測LDAMP 網絡每一層的均方誤差(Mean square error,MSE)性能[20].在數值仿真實驗中,在固定DnCNN 神經網絡和LDAMP 網絡的層數,選擇高斯測量矩陣,在無和有外部測量噪聲兩種情況下,分別對4 個量子位的量子本征態、疊加態、對角混合態和一般混合態的密度矩陣參數估計進行結果和性能分析,并與其他典型的重建算法對密度矩陣參數估計的性能進行了對比研究.

本文結構安排如下:第1 節概述了基于壓縮感知的量子狀態估計作為一個信號恢復問題,第2 節介紹了應用于量子狀態估計的DAMP 信號恢復算法,第3 節具體描述了LDAMP 網絡的實現和DnCNN 神經網絡的結構及其訓練過程,第4 節給出了對DnCNN 訓練后模型的測試結果和量子態估計數值模擬實驗結果及分析,第5 節是結論.

1 基于壓縮感知的量子態密度矩陣估計

壓縮感知是近10 多年來在信號處理領域誕生的一種新的信號恢復理論.它主要是利用信號s∈CN的M(遠遠小于完備測量需要的N)個隨機線性測量值y,建立欠定線性方程組y=As(y∈CM),并通過優化算法來高精度重構求解出原始信號s,其中A∈CM×N,M＜N為測量矩陣.在量子態估計中,原始信號為密度矩陣ρ∈Cd×d,它與量子系統波函數之間的關系為:

式中,|ψi〉為系統的波函數,pi表示波函數的概率,d為密度矩陣的維數.將密度矩陣寫成向量表達的形式是ρ=ψ·ψ*,其中ψ=當量子系統的量子位數為n時,密度矩陣的維數d=2n.由于神經網絡無法直接處理復數信號的去噪,在本文中僅對實數密度矩陣進行估計.在基于壓縮感知的量子態估計中,測量矩陣A需要滿足限制等距特性才可以唯一確定d2個待估計的密度矩陣元素,人們通常采用的是泡利測量矩陣[21].由于隨機高斯矩陣參數均為實數并且具有較好的重構效果[22],本文中在RIP 條件下采用隨機高斯矩陣來構造測量矩陣,其設計方法為:構造一個M ×N大小的矩陣A,使A中的每一個元素獨立的服從均值為0,方差為 1 /M的高斯分布,即:

式中,A的行數與列數的比值定義為采樣率η=M/N,并且有N=d2.

考慮從有外部測量干擾的線性度量中恢復密度矩陣ρ∈Rd×d的問題:

式中,vec(·) 表示將一個矩陣按列的方向組合成一個列向量,w∈Rm為測量噪聲并且通常被假設為獨立且同分布的高斯噪聲.定義測量噪聲w～N(0)為加性高斯白噪聲(Additive white Gaussian noise,AWGN),其中γw為噪聲標準差.在本文的模擬實驗中,采用含測量噪聲信號y和理想測量信號y0=A·vec(ρ) 之間的信噪比(Signal noise ratio,SNR)作為噪聲強度,計算公式為:

式中,y(i,j)和y0(i,j) 分別為含測量噪聲信號和理想測量信號在向量中 (i,j) 點處的值.

利用正則化二次損失最小化方法解決該線性逆問題,可以通過求解一個凸優化問題計算得到vec(ρ)的估計值[23-24]:

式中,λ＞0 為正則化參數.然而這個極小化問題是一個凸優化問題,在大規模問題中,由于數據維度較大,常規求解算法中,如內點法等的算法復雜度較大,求解起來非常耗時.這使得眾多研究人員通過簡單的基于梯度的方法來求解式(5).

2 DIT和DAMP 算法

在眾多基于梯度的算法中,最受關注的一類方法是迭代閾值(Iterative threshold,IT)算法.為了方便表示,定義s=vec(ρ).當待估計的密度矩陣為ρ0時,稱s0=vec(ρ0) 為待估計的信號.從s0=0和z0=0開始,迭代公式為:

式中,sl是l次迭代密度矩陣的估計值.zl是l次迭代的殘差,如果密度矩陣恢復過程是無噪聲的,并且算法性能執行得很好,它將收斂于0.η(·) 稱為閾值函數,它是一個被應用到矢量的分量元素上的標量非線性函數.λl是l次迭代閾值函數使用的參數.

在信號恢復中,閾值函數的選擇非常重要,常見的有軟閾值函數(7)等.其中符號 (w)+表示w ≥0時結果為w,否則結果為0.另外一種實現閾值函數的方法是使用降噪器Dσ?l,此時閾值參數λl的含義為輸入降噪器的信號的所含高斯噪聲的標準差估計,并且計算公式為它隨著迭代次數的變化而變化.利用降噪器實現閾值函數的迭代閾值算法稱為基于去噪的迭代閾值(Denoisingbased iterative threshold,DIT)算法[17],迭代公式為:

基于不同的降噪器,DAMP 包含許多算法[27],包括高斯-AMP (Gauss-AMP)、雙邊-AMP (Bilateral-AMP)、非局部平均-AMP (Non-local means AMP,NLM-AMP)和三維塊匹配-AMP (Block matching 3D AMP,BM3D-AMP)[28]等.本文采用的降噪器和散度計算都是通過設計并訓練一個深度卷積神經網絡DnCNN 來實現.同時通過設計一個學習的基于去噪的近似消息傳遞LDAMP 網絡,來實現算法1 的DAMP 算法,并通過多個相同結構的的級聯,來獲得高精度的信號s0即vec(ρ0) 的估計,得到密度矩陣ρ0的估計.

本文通過LDAMP 網絡,使用量子系統輸出的測量值,來實現對量子態密度矩陣估計,具體流程如下:

步驟1.根據生成DnCNN 神經網絡的訓練集,驗證集和測試集,具體過程在第3.3 節;

步驟2.在9 個不同噪聲標準差范圍下,訓練出相應的DnCNN 神經網絡,訓練完成后利用測試集對網絡進行測試;

步驟3.對于待估計的密度矩陣ρ0,在不同采樣率下利用高斯測量算符獲取的輸出測量值y0.對于含噪聲情況下測量值,通過y=awgn(y0,SNR) 添加固定SNR數值的高斯噪聲獲得好噪聲測量值y;

步驟4.設計一個包含訓練好的DnCNN 網絡和實現DAMP 算法的10 層LDAMP 網絡,網絡各層中的DnCNN 是根據當前層的噪聲標準差估計σ?落入的9 個范圍來選定.LDAMP 網絡的輸入為測量值y0或y;

步驟5.LDAMP 網絡最后的輸出為根據輸入測量值y0或y得到的估計的密度矩陣.

3 LDAMP和DnCNN 網絡的結構設計及其訓練

第3.1 節對LDAMP 網絡的結構進行設計;第3.2 節進行DnCNN 降噪器及其中的卷積神經網絡的結構設計;第3.3 節進行DnCNN 降噪器中神經網絡的訓練過程.

3.1 LDAMP 網絡的結構設計

LDAMP 網絡由L層相同的AMP 網絡結構級聯而成,其中,LDAMP 網絡單層的結構圖如圖1所示.每層網絡包含兩個在固定噪聲標準差區間下訓練好的DnCNN 降噪器,一個用于計算每層AMP網絡的輸出sl+1,另一個用于實現散度圖1中的xl=sl+AHzl為LDA MP網絡的第(l+1) 層中DnCNN 降噪器的輸入信號,v?l為降噪器中DnCNN 卷積神經網絡的輸出,它表示對有效噪聲vl的估計.

圖1 LDAMP 中第 l 級網絡結構圖Fig.1 Structure of the l-level network in the LDAMP

需要指出的是,LDAMP 網絡中只有DnCNN降噪器是由神經網絡設計而成,而網絡的其他部分只是對DAMP 算法的實現.

對于L層的LDAMP 網絡,可以使用不同的方法來訓練,包括端到端訓練,逐層訓練和逐降噪器訓練,其中,端到端訓練是指將L層的LDAMP網絡視作一個整體,同時訓練網絡的所有權值.這是訓練神經網絡的標準方法.逐層訓練是指每次訓練LDAMP 網絡中的一層AMP 網絡來恢復信號,固定這些權值,然后添加一層AMP 網絡,訓練產生的2 層網絡的第2 層來恢復信號,再固定這些權值,重復操作直到已經訓練一個L層LDAMP 網絡.逐降噪器訓練是指將DnCNN 降噪器從網絡中單獨出來,并在不同噪聲標準差范圍區間下訓練每個降噪器的AWGN 去噪問題,從而得到多個不同去噪水平的降噪器,以供LDAMP 網絡中的各層選擇,即每層AMP 網絡,根據當前層的噪聲標準差的估計,來選擇使用哪一個降噪器.

本文采用的逐降噪器訓練方法是最小均方誤差(Minimum mean squared error,MMSE)[17]最優的.具體訓練過程為:首先,對噪聲水平的預期范圍進行離散化,將噪聲標準差[0,2]范圍內的噪聲分成多個小范圍;然后,在這些小范圍噪聲水平下訓練DnCNN 降噪器,得到多個訓練好的降噪器模型;最后,LDAMP 網絡實現時,每層網絡根據本層的噪聲標準差估計落在某個區間內,來選擇在該噪聲標準差區間下訓練好的降噪器模型.LDAMP網絡易于訓練,可以應用于各種不同的測量矩陣,并帶有一個可以準確預測其性能的狀態演化框架.

狀態演化(State evolution,SE)是一個可以預測LDAMP 網絡各級的輸出與真實信號之間MSE性能的分析框架.它由一系列SE 方程組成:

3.2 DnCNN 降噪器的結構設計

在DnCNN 神經網絡結構設計上,DnCNN 網絡源于對VGG 網絡的改進,去除了池化層和全連接層,在卷積層(Convolution,Conv)和修正線性單元(Rectified linear unit,ReLU)[29]之間加入了批歸一化(Batch normalization,BN)[30].這種改變可以減輕內部協變量移位[18]帶來的影響,從而提高網絡的學習收斂速度.在模型學習中,DnCNN 借鑒了ResNet 的殘差學習方法[31-33],來提高訓練速度和去噪性能.

圖2 為DnCNN 降噪器的網絡結構圖,圖3 是DnCNN 降噪器輸入變量的尺寸變換過程圖.輸入矢量的維數為d×d,其中d=2n,n為量子態的位數.深度為D的DnCNN 神經網絡,在本文應用中,D取值為20.本文設計的DnCNN 有三種不同的網絡層,具體排列順序為:第1 層為卷積層+修正線性單元(Conv+ReLU):使用64 個大小為3×3×1的卷積核(或稱為濾波器),生成64 個特征圖.然后,使用修正線性單元進行非線性處理.第2～(D-1)層為卷積層+批歸一化+修正線性單元(Conv+BN+ReLU),使用64 個大小為 3×3×64 的卷積核,在卷積層和ReLU 層之間加入BN 層.最后一層為卷積層(Conv),使用1 個大小為 3×3×64 的卷積核重構輸出.

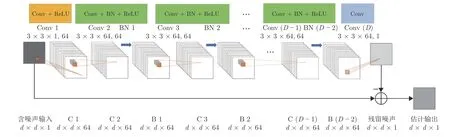
圖2 DnCNN 降噪器的網絡結構圖Fig.2 Network structure of the DnCNN denoiser

DnCNN 神經網絡的輸入是有噪聲的信號矩陣x∈Rd×d,所以LDAMP 網絡各層把數據輸入到DnCNN 神經網絡之前,需要將列向量變成原始信號大小的矩陣形式,變換過程如圖3 所示.含噪聲輸入的矩陣x和向量xl分別為:

圖3 DnCNN 降噪器輸入變量的尺寸變換過程Fig.3 Size transformation process of input variable of the DnCNN denoiser

它是估計噪聲信號R(x;Θ) 與真實噪聲信號v=x-s0之間的均方誤差.其中,Q是批大小(Batch Size),Θ 是DnCNN 神經網絡中可以調整的參數,包括網絡的權值和偏置,訓練次數和目標誤差等.

在許多信號恢復算法中,通常要求輸出信號的尺寸與輸入信號的尺寸一致,這可能會導致恢復的矩陣信號中邊界元素值受到較大影響,也就是產生邊界偽影.為了保證隱含層的每個特征信號與輸入信號的尺寸大小相同,在DnCNN 神經網絡的每個卷積層中進行卷積運算之前,對輸入卷積層的信號采用簡單的零填充策略,不過這種零填充策略不會產生任何邊界偽影[18].

3.3 DnCNN 神經網絡訓練過程

在對DnCNN 神經網絡進行訓練時,采用的樣本數據的尺寸大小為 24×24=16×16,也就是4個量子位的密度矩陣.對樣本數據加入不同標準差范圍下的高斯噪聲作為訓練輸入,原始樣本數據作為訓練輸出目標,在未知高斯噪聲水平下訓練DnCNN 神經網絡.為了訓練更小噪聲范圍下的DnCNN 網絡,將噪聲標準差范圍[0,2]劃分成9個小范圍,具體分段結點為0、0.005、0.01、0.03、0.05、0.1、0.3、0.5、1和2,并在這9 個小范圍噪聲水平下分別訓練了DnCNN 網絡.然后LDAMP 網絡根據各級的噪聲標準差估計σ? 的大小選擇對應的DnCNN 模型.訓練和測試過程中,樣本數據包含滿足和近似滿足量子態密度矩陣性質的矩陣,其中滿足性質的兩種量子態的密度矩陣生成公式為:

式中,φr為d×r的Wishart 矩陣,并且矩陣內各元素滿足高斯分布[35].r=1 時,為疊加態密度矩陣,r ＞1時為一般混合態密度矩陣.

本文研究的另外兩種量子態還包括本征態和對角混合態,其中本征態密度矩陣為僅有對角線某一位置有元素為1,其他位置元素均為0 的矩陣,對角混合態密度矩陣為僅在對角線上所有位置有非0 元素,且對角線所有元素之和為1,其他位置元素均為0 的矩陣.樣本數據中近似滿足性質的矩陣是指在構造樣本數據時,改變部分滿足性質的密度矩陣中的元素,加入一些噪聲干擾,使矩陣的跡在[0,1]之間且近似共軛對稱的半正定矩陣.在構造過程中,采用[0,1]之間的隨機數乘以原始密度矩陣或在原始矩陣生成過程中給矩陣φr的共軛轉置矩陣添加噪聲干擾.值得注意的是,訓練集和測試集中近似滿足性質的密度矩陣所占的比例在30%～50%可以取得較好的估計效果,另外[0,0.5]之間的隨機數應多于(0.5,1]之間的隨機數.這種構造方法的原因是因為LDAMP 網絡具有數層相同的結構,網絡的初始輸入s0=vec(ρ0) 為零向量,網絡的最終輸出為估計的密度矩陣,所以網絡進行密度矩陣估計是各層網絡漸近逼近真實密度矩陣的過程,因此需要大量的中間估計結果和少量的零矩陣包含在訓練樣本集中.

在訓練DnCNN 時,本文使用了9 900×128=1 267 200 個樣本用于訓練,1 100×128=140 800 個樣本用于驗證和11 × 128=1 408 個樣本矩陣用于測試.訓練集、驗證集及測試集中4 種量子態密度矩陣的比例為本征態:對角混合態:疊加態:一般混合態=1:2:4:4.所有的樣本矩陣在生成時都是無噪聲樣本,而在訓練、驗證和測試時,會在對應的噪聲水平范圍內加入噪聲.為了獲取足夠的空間信息進行去噪,將DnCNN 神經網絡的深度設置為20 層.采用了一種魯棒的初始化方法MSRA[36]來初始化DnCNN 神經網絡權值,并采用權值衰減為0.0001、動量為0.9、小批量尺寸為128 的帶動量的隨機梯度下降法(Stochastic gradient descent with momentum,SGDM)訓練網絡.為每個小范圍噪聲水平下的神經網絡設置的最大訓練次數為50,最大允許無用訓練次數(Max bad epochs,MBE)為2,初始無用訓練次數(Bad epochs,BE)為0.在訓練過程中,初始最小驗證誤差采用驗證集驗證未訓練的網絡得到,后續過程中,網絡訓練一次就驗證一次得到新的驗證誤差,并將新的驗證誤差與上一次的驗證誤差相比,如果小于上一次的驗證誤差就將此次驗證誤差設置為最小驗證誤差并將BE 清零,否則最小驗證誤差不變并將BE 加1.當BE 大于等于MBE 時,網絡就減小學習速率,并將BE 清零.學習速率變化過程為初始值0.001 衰減為0.0001,最后衰減至0.00001.當學習速率衰減為0.00001且BE 大于等于MBE 時,DnCNN 神經網絡的訓練結束.在實驗中,使用Matlab 中的MatCov-Net 工具箱[37]來實現DnCNN 神經網絡.所有實驗均在Intel(R) Core(TM) i7-8700K CPU 3.70 GHz、NVIDIA GeForce GTX 1 080 GPU 的PC 上運行的Matlab (R2018b)環境下進行.所有9 個小范圍噪聲水平下的20 層DnCNN 網絡的GPU 訓練時間需要59 小時左右.

4 量子態估計仿真實驗及其結果分析

本節對本文提出的LDAMP 網絡的量子態估計性能,在不同參數下,進行了數值性能對比實驗,進行3 個實驗:

1)不同噪聲標準差區間下,對所設計訓練出的20 層DnCNN 神經網絡降噪器去噪性能的測試實驗;

2)本文的LDAMP 網絡與其他5 種不同方法對量子態密度矩陣估計的性能對比實驗;

3)不同測量噪聲以及不同采樣率分別對LDAMP網絡估計量子態密度矩陣性能的影響實驗.

實驗中,量子狀態測量值y是根據式(3)計算:y=A·vec(ρ0)+w,其中A為隨機高斯測量矩陣,w～N(0)表示測量過程中產生的高斯噪聲,ρ0為真實密度矩陣,可以從本征態、疊加態、對角混合態和一般混合態密度矩陣中選取.定義了三個性能指標來衡量實驗結果:

當MSE 以dB 作為單位時,定義為:

3)估計的密度矩陣與真實密度矩陣之間的保真度(Fidelity)[38]:

式中,保真度的范圍是[0,1],并且當2 個矩陣完全相同時,保真度為1[39].

4.1 DnCNN 去噪性能的測試實驗

圖4 為使用11 × 128=1408 個隨機樣本矩陣,分別測試噪聲水平分別從[0,0.005],(0.005,0.03],···,(1,2]共9 個范圍情況下,對訓練后得到的20 層DnCNN 進行去噪性能的測試實驗的誤差曲線圖,其中方形實線表示網絡輸入樣本與對應的無噪聲樣本之間的平均均方誤差MSE (dB);圓圈虛線為網絡輸出樣本與對應的無噪聲樣本之間的平均均方誤差MSE (dB);三角形實線是輸出誤差與輸入誤差之間的MSE 比值變化曲線.由圖4 可以看出,網絡輸出誤差始終小于輸入誤差,并且隨著噪聲標準差的增加,輸出誤差與輸入誤差之間的比值逐漸減小:從[0,0.005]區間的0.5956 減小至(1,2]區間的0.0311.這說明,當輸入噪聲很小時,輸出誤差仍然能夠濾掉接近一半噪聲,隨著噪聲的增加,去噪效果越明顯.表明經過訓練后的DnCNN 降噪器擁有良好的去噪效果.

圖4 DnCNN 降噪器的MSE 性能Fig.4 MSE performance of the DnCNN denoiser

4.2 LDAMP 網絡與其他方法的對比實驗

本節中將本文的LDAMP 網絡與ADMM 算法,以及其他4 種DAMP 算法(BM3D-AMP、NLMAMP、Gauss-AMP和Bilateral-AMP)對量子態估計的性能,進行對比實驗.實驗中采用的樣本為對角混合態密度矩陣.分別在采樣率從0.05 每隔0.05增加到0.5,測量噪聲強度固定為SNR=40 dB 情況下,不同量子態估計方法的歸一化距離隨采樣率變化情況,實驗結果如圖5 所示.固定采樣率η=0.1,不同量子態估計方法的MSE (dB)性能隨SNR 變化情況如表1 所示.由圖5 可以看出,在每一個采樣率下,LDAMP 網絡的性能是所有算法中最好的,并且在采樣率為0.15 時,就能夠達到10-3的性能.由表1 可以看出,在所有不同噪聲等級干擾和無噪聲情況下,LDAMP 網絡的估計性能均優于其他方法,并且在無噪聲干擾下的MSE (dB)為-41.0905 dB,估計誤差達到 1 0-4量級.

表1 當 η=0.1 時,LDAMP 網絡和其他方法的MSE (dB)性能比較Table 1 Comparison of MSE (dB) performance between LDAMP network and other methods with η=0.1

圖5 當SNR=40 dB 時,LDAMP 網絡和其他方法的歸一化距離性能對比Fig.5 Comparison of normalized distance performance between LDAMP network and other methods with SNR=40 dB

4.3 LDAMP 網絡的量子態估計實驗

本節采用本文設計出的具有20 層DnCNN 以及10 層算法迭代的LDAMP 網絡,在無和有噪聲的2 種情況下,分別對本征態、疊加態、對角混合態和一般混合態的估計進行了性能對比實驗.影響狀態估計性能的因素有采樣率的多少和噪聲的大小,共進行了4 個實驗.

1)不同采樣率下無和含固定測量噪聲的量子狀態估計實驗

在采樣率從0.05 每隔0.05 增加到0.5,分別在無和含固定測量噪聲SNR=40 dB 兩種情況下,對4 種不同算法的量子狀態進行了網絡訓練設計,網絡的估計結果與真實狀態之間的歸一化距離變化過程如圖6 所示.從圖6 可以看出,隨著采樣率的增加,所有狀態估計的歸一化距離呈下降趨勢,估計效果逐漸變好.由于測量噪聲的存在,所有狀態的估計結果均略差于無噪聲情況下的狀態估計.其中,本征態的估計最為準確,歸一化距離均可以在最低采樣率0.05 時達到 1 0-4量級,其在無噪聲情況下的保真度為0.999993,有噪聲情況下的保真度為0.989028.對角混合態的估計次之,其在0.15 采樣率時無噪聲情況下的歸一化距離(保真度)才達到0.0017 (0.999898).這2 種量子狀態具有較為簡單的密度矩陣結構,因此在估計時也達到了較好的估計效果.在無噪聲情況下,疊加態在采樣率0.3 時的歸一化距離(保真度)達到0.0037 (0.980570);一般混合態在采樣率0.5 時的歸一化距離(保真度),達到0.0198 (0.992958).在采樣率小于0.3 時,對角混合態的估計效果不如一般混合態;當采樣率大于0.3 時,對角混合態效果優于一般混合態.對于這種現象,經過采用多個不同密度矩陣的驗證,可以得出以下原因:在采樣率較小時,兩種狀態的估計效果均不理想,但是由于疊加態密度矩陣中元素數值相對一般混合態中的元素數值較大一些,所以計算出的歸一化距離的值會更大,而采樣率變大后,兩種狀態的估計效果均逐漸變好,由于疊加態相對于一般混合態的密度矩陣結構更為簡單,此時疊加態的估計效果明顯優于一般混合態,其歸一化距離更低.

圖6 LDAMP 網絡對不同量子態密度矩陣估計的歸一化距離性能對比Fig.6 Comparison of normalized distance performance of LDAMP network for estimation of density matrices of different quantum states

2)三種采樣率及噪聲固定下不同層數的LDAMP 網絡的性能實驗

圖7 為固定噪聲SNR=40 dB,采樣率分別取0.05、0.1和0.2 三種情況下,不同層數的LDAMP 網絡估計效果與式(10)和式(11)所示的SE方程的MSE (dB)性能對比的實驗結果,其中虛線為SE 方程在三個不同采樣率下的性能,實線為本文設計的LDAMP 網絡所對應的性能Sim.由圖7可以看出,在采樣率低于0.2 時,LDAMP 網絡在10 層內收斂;而采樣率大于0.2 時,對于混合態和疊加態,LDAMP網絡則需要更多的層數達到收斂,這也與密度矩陣的復雜度相關,同時表明本文設計的LDAMP 網絡的高效性.

圖7 當SNR=40 dB 時,不同采樣率下LDAMP 網絡的仿真(Sim)狀態演化方程的MSE (dB)性能對比Fig.7 Comparison of MSE (dB) performance between simulation (Sim) and SE analysis of LDAMP network for different sampling ratios with SNR=40 dB

3)固定采樣率在無和有噪聲下對角混合態的估計性能對比實驗

圖8 為固定采樣率0.1,在無和分別含SNR=30 dB和SNR=40 dB 測量噪聲的情況下,對角混合態真實密度矩陣ρ3測量值的柱狀圖.圖8 中3 個測量值之間的對比表現出不同大小測量噪聲對真實測量值的影響效果.由圖8 可以看出,30 dB 明顯比40 dB 等級的噪聲影響更大,這種影響持續體現在對真實量子態的估計上.

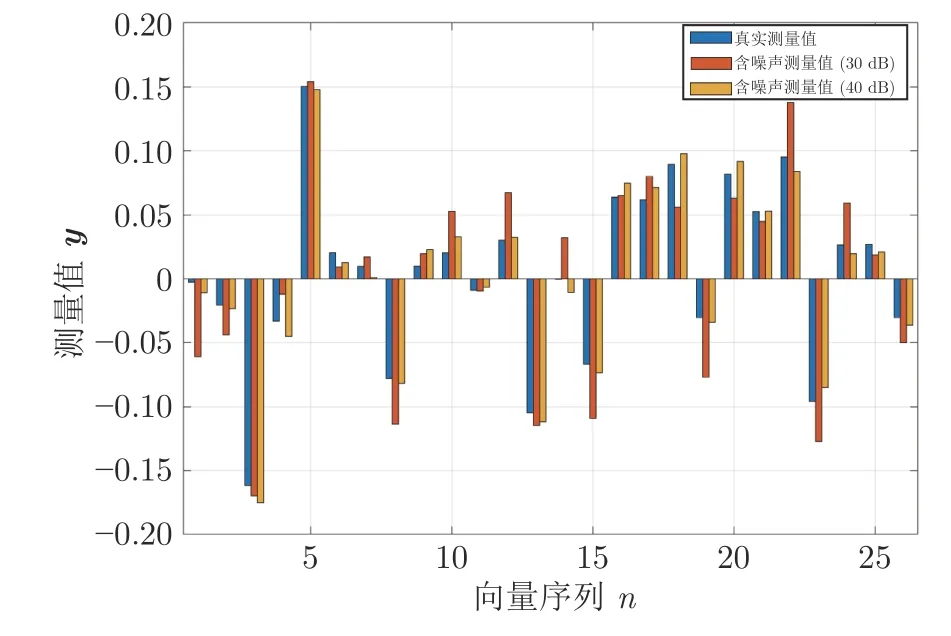
圖8 當 η=0.1 時,對角混合態密度矩陣 ρ3 的真實測量值與含噪聲測量值對比Fig.8 Comparison between the real measured values of diagonal mixed state density matrix ρ3 and the measured values with noise inη=0.1

圖9 為相同情況下,對角混合態真實密度矩陣ρ3與密度矩陣估計、(w=30 dB)和(w=40 dB)的模值元素分布圖.估計出來的3 個密度矩陣與ρ3之間的歸一化距離分別為0.1492、0.3197和0.1614.

圖9 當 η=0.1 時,對角混合態密度矩陣 ρ3 及其在無和含測量噪聲下估計矩陣的模值分布Fig.9 Diagonal mixed state density matrix ρ3 and its modulus distribution of estimation matrix without and including measurement noise with η=0.1

4) 3 種采樣率下4 種不同量子態在不同噪聲的估計性能實驗

為了研究測量噪聲和采樣率對量子態估計的具體影響,還進行了采樣率分別為0.05、0.1和0.2 時,4 種不同量子態估計后的MSE (dB)隨測量噪聲大小的變化的實驗,實驗結果如圖10 所示.由圖10可以看出,在采樣率和噪聲水平分別固定時,所有量子態估計的MSE 均隨另一個未固定量的增加而減小,其中SNR 增加時表示噪聲水平降低.LDAMP 網絡的性能可以隨著采樣率的增加而提高.不同量子態的表現也有差異,對于本征態,LDAMP網絡在采樣率η=0.1 的情況下,就能夠獲得優良的性能.而對于其他3 種量子態,則需要增加采樣率來達到期望的估計效果.

圖10 不同采樣率下LDAMP 網絡對4 種量子態密度矩陣估計時的MSE 性能Fig.10 MSE performance of the LDAMP network for the estimation of four quantum state density matrices with different sampling ratios

5 結束語

本文訓練出一個具有20 層的降噪卷積神經網絡(DnCNN),與基于去噪的近似消息傳遞(DAMP)算法相結合,設計出一個10 層的基于學習去噪的近似消息傳遞(LDAMP)網絡,并將其應用于量子狀態估計中.本文提出的LDAMP 網絡在量子態估計中的性能,優于基于壓縮感知理論最先進的三維塊匹配近似消息傳遞BM3D-AMP 信號恢復算法和ADMM 算法,為采用深度學習網絡進行量子態估計開辟了一條新的路徑.更加深入的研究是帶有虛部的深度學習網絡的量子態估計,以及實現在線量子態估計[40]的深度學習網絡的實現.